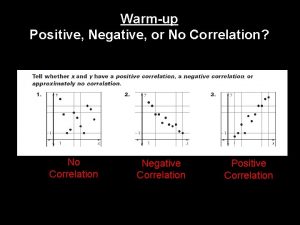
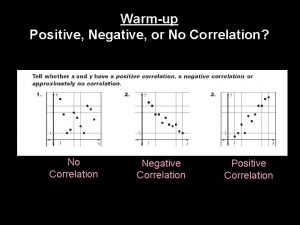
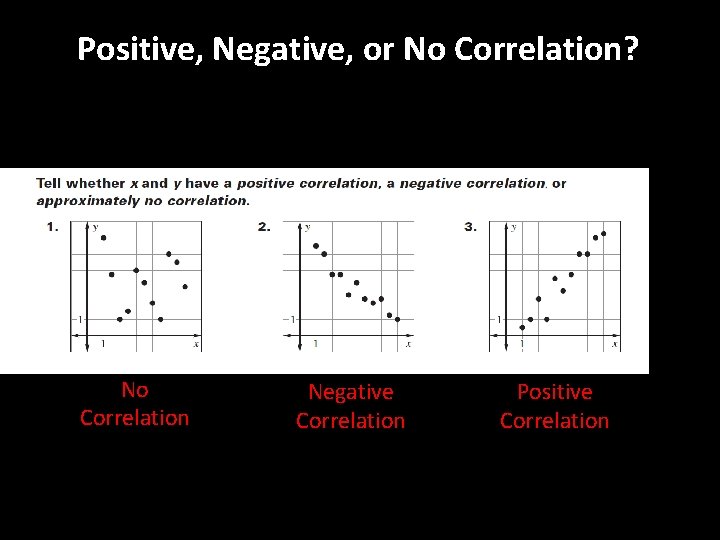
Positive Negative or No Correlation No Correlation Negative

Positive, Negative, or No Correlation? No Correlation Negative Correlation Positive Correlation

Positive, Negative, or No Correlation? 4. Number of Homeless People vs. Crime Rate Positive Correlation 5. Number of Storks in Denmark vs. the Number of children born No Correlation 6. Age of Driver vs. Cost of Insurance Negative Correlation

Put the following correlation values in order from weakest to strongest. 0. 29, -0. 87, -0. 41, 0. 03, -0. 59, -0. 92, 0. 68 0. 03, 0. 29, -0. 41, -0. 59, 0. 68, -0. 87, -0. 92 **Even though the #s are negative, the strong correlations are closer to 1**

Daily Check

Line of Best Fit Linear Regression

A little vocab… • The line of best fit is the line that lies as close as possible to all the data points. • Regression is a method used to find the equation of the line of best fit.

Example 1: The environment club is interested in the relationship between the number of canned beverages sold in the cafeteria and the number of cans that are recycled. The data they collected are listed in this chart. # of Canned Drinks Sold 18 15 19 8 10 13 9 14 # of Cans Recycled 8 6 10 6 3 7 5 4 a) Plot the points to make a scatter plot. b) Use a straightedge to approximate the line of best fit by hand. c) Find an equation of the line of best fit for the data.

Example 1:

Entering Data : TI 36 X - Pro 1. 2. 3. 4. DATA 4 (this will clear all the data) DATA (type in data) 2 nd DATA Lin. Reg ax + b (for linear regression) Exp. Reg ab^x (for exponential regression) L 1 L 2 ONE YES CALC 5. a = b= r= 6. The equation of the line is y = ax + b. 7. Correlation Coefficient is r.

Example 2: The table shows the total outstanding consumer debt (excluding home mortgages) in billions of dollars in selected years. (Data is from the Federal Reserve Bulletin. ) L 1 L 2 0 585 5 789 10 1096 15 1693 18 1987 Let x = 0 correspond to 1985. Year Consumer Debt 1985 1990 1995 2000 2003 585 789 1096 1693 1987 a) Find the regression equation appropriate for this data set. Round values to two decimal places.

Example 2: Year Consumer Debt 1985 1990 1995 2000 2003 585 789 1096 1693 1987 b) Find and interpret the slope of the regression equation in the context of the scenario. 79. 86 represents the increase in consumer debt each year. c) Find the approximate consumer debt in 1998. d) Find the approximate consumer debt in 2008.

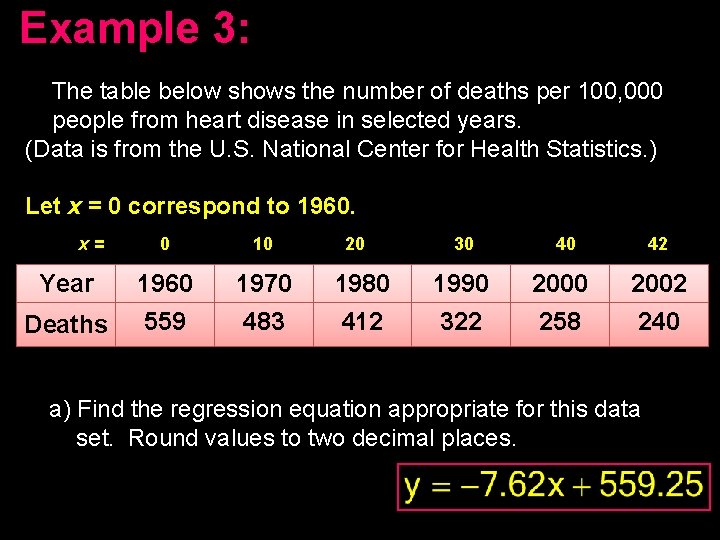
Example 3: The table below shows the number of deaths per 100, 000 people from heart disease in selected years. (Data is from the U. S. National Center for Health Statistics. ) Let x = 0 correspond to 1960. x= 0 10 20 30 40 42 Year 1960 1970 1980 1990 2002 Deaths 559 483 412 322 258 240 a) Find the regression equation appropriate for this data set. Round values to two decimal places.

Example 3: Year 1960 1970 1980 1990 2002 Deaths 559 483 412 322 258 240 b) Find and interpret the slope of the regression equation in the context of the scenario. -7. 62 is the decrease in deaths caused by heart disease each year. c) Find the approximate number of deaths due to heart disease in 1995. d) Find the approximate number of deaths due to heart disease in 2008.

Classwork Linear Regression