Canonical Correlation Analysis An overview with application to

Canonical Correlation Analysis: An overview with application to learning methods By David R. Hardoon, Sandor Szedmak, John Shawe-Taylor School of Electronics and Computer Science, University of Southampton Published in Neural Computaion, 2004 Presented by: Shankar Bhargav

Canonical Correlation Analysis Measuring the linear relationship between two multi dimensional variables Finding two sets of basis vectors such that the correlation between the projections of the variables onto these basis vectors is maximized Determine Correlation Coefficients

Canonical Correlation Analysis More than one canonical correlations will be found each corresponding to a different set of basis vectors/Canonical variates Correlations between successively extracted canonical variates are smaller and smaller Correlation coefficients : Proportion of correlation between the canonical variates accounted for by the particular variable.

Differences with Correlation Not dependent on the coordinate system of variables Finds direction that yield maximum correlations

Find basis vectors for two sets of variables x, y such that the correlations between the projections of the variables onto these basis vector Sx = (x. wx) and Sy = (y. wy) ρ= ρ= E[Sx Sy ] √ E[Sx 2] E[Sy 2] E[(x. T wx y. T wy)] √E[(x. T wx) ] E[(y. T wy)]

ρ= max wx wy E[wx. Tx y. T wy] √E[wx. Tx x. T wx ] E[wy. T y y. T wy] wx. TCxy wy √ wx. TCxxwx wy. TCyy wy Solving this with constraint wx. TCxxwx =1 wy. TCyy wy=1

Cxx-1 Cxy. Cyy-1 Cyx wx = ρ2 wx Cyy-1 Cyx. Cxx-1 Cxy wy= ρ2 wy Cxy wy = ρλx Cxx wx Cyx wx = ρλy Cyy wy λx=λy-1= wy. TCyywy √ wx. TCxxwx

CCA in Matlab [ A, B, r, U, V ] = canoncorr(x, y) x, y : set of variables in the form of matrices § § Each row is an observation Each column is an attribute/feature A, B: Matrices containing the correlation coefficient r : Column matrix containing the canonical correlations (Successively decreasing) U, V: Canonical variates/basis vectors for A, B respectively

Interpretation of CCA Correlation coefficient represents unique contribution of each variable to relation Multicollinearity may obscure relationships Factor Loading : Correlations between the canonical variates (basis vector) and the variables in each set Proportion of variance explained by the canonical variates can be inferred by factor loading

Redundancy Calculation Redundancy left =[ ∑ (loadingsleft 2)/p]*Rc 2 Redundancy right =[ ∑ (loadingsright 2)/q]*Rc 2 p – Number of variable in the first (left) set of variables q – Number of variable in the second (right) set of variables Rc 2 – Respective squared canonical correlation Since successively extracted roots are uncorrelated we can sum the redundancies across all correlations to get a single index of redundancy.

Application Kernel CCA can be used to find non linear relationships between multi variates Two views of the same semantic object to extract the representation of the semantics n n Speaker Recognition – Audio and Lip movement Image retrieval – Image features (HSV, Texture) and Associated text

Use of KCCA in cross-modal retrieval n n n 400 records of JPEG images for each class with associated text and a total of 3 classes Data was split randomly into 2 parts for training and test Features Image – HSV Color, Gabor texture Text – Term frequencies n Results were taken for an average of 10 runs

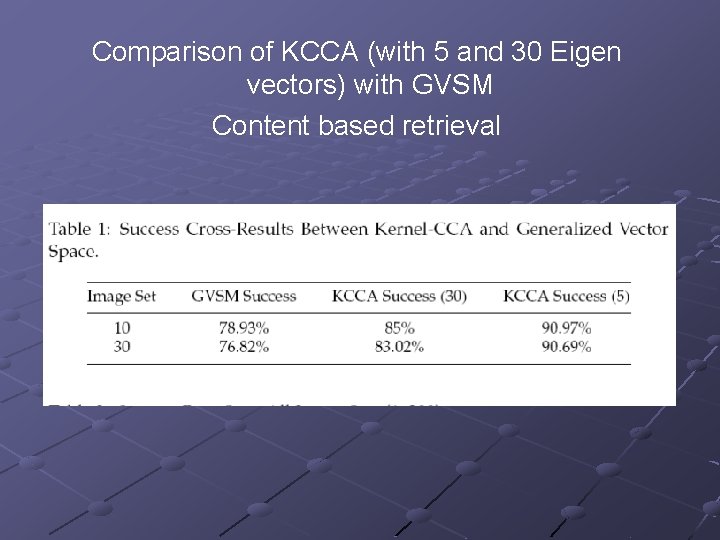
Cross-modal retrieval Content based retrieval: Retrieve images in the same class Tested with 10 and 30 images sets n where countjk = 1 if the image k in the set is of the same label as the text query present in the set, else countjk = 0.

Comparison of KCCA (with 5 and 30 Eigen vectors) with GVSM Content based retrieval

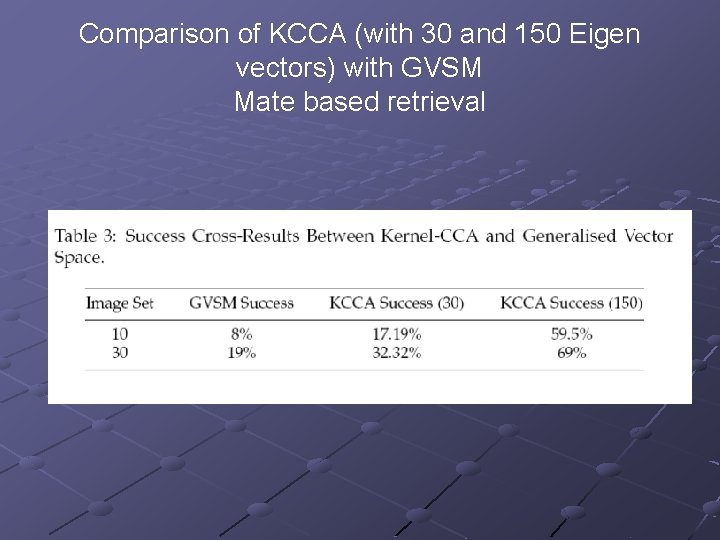
Mate based retrieval Match the exact image among the selected retrieved images Tested with 10 and 30 images sets n where countj = 1 if the exact matching image was present in the set else it is 0

Comparison of KCCA (with 30 and 150 Eigen vectors) with GVSM Mate based retrieval

Comments The good n n Good explanation of CCA and KCCA Innovative use of KCCA in image retrieval application The bad n The data set and the number of classes used were small n The image set size is not taken into account while calculating accuracy in Mate based retrieval n Could have done cross-validation tests

Limitations and Assumptions of CCA At least 40 to 60 times as many cases as variables is recommended to get relliable estimates for two roots– Barci. Kowski & Stevens(1986) Outliers can greatly affect the canonical correlation Variables in two sets should not be completely redundant

Thank you