Nondeterministic Finite Automaton NFA Definition An NFA is

Nondeterministic Finite Automaton (NFA) Definition: An NFA is a TG with a unique start state and a property of having single letter as label of transitions. An NFA is a collection of three things 1) Finite many states with one initial and some final states 2) Finite set of input letters, say, ={a, b, c} 3) Finite set of transitions, showing where to move if a letter is input at certain state ( is not a valid transition), there may be more than one transition for certain letters and there may 1 not be any transition for certain letters.

Observations It may be observed, from the definition of NFA, that the string is supposed to be accepted, if there exists at least one successful path, otherwise rejected. It is to be noted that an NFA can be considered to be an intermediate structure between FA and TG. The examples of NFAs can be found in the following 2

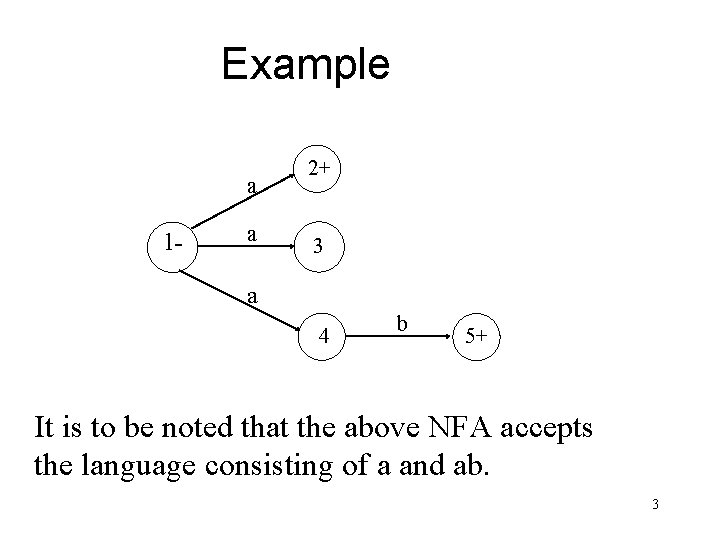
Example a 1 - a 2+ 3 a 4 b 5+ It is to be noted that the above NFA accepts the language consisting of a and ab. 3

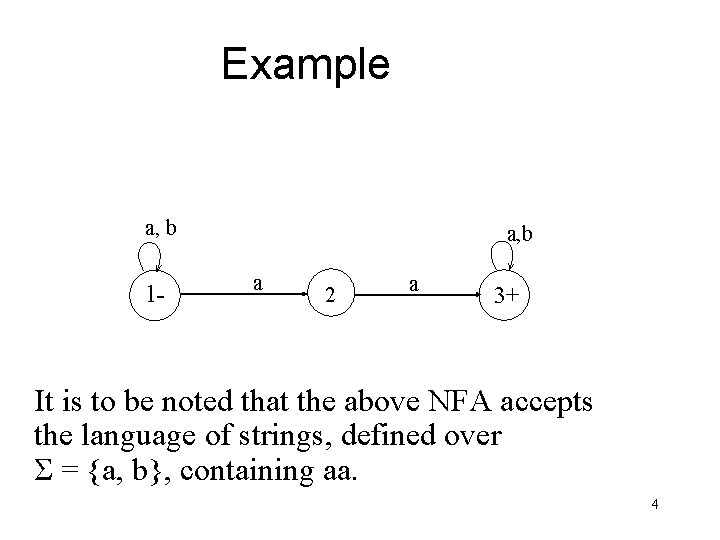
Example a, b 1 - a, b a 2 a 3+ It is to be noted that the above NFA accepts the language of strings, defined over Σ = {a, b}, containing aa. 4

Note • It is to be noted that NFA helps to eliminate a loop at certain state of an FA. This process is done converting the loop into a circuit. But during this process the FA remains no longer FA and is converted to a corresponding NFA, which is shown in the following example. 5

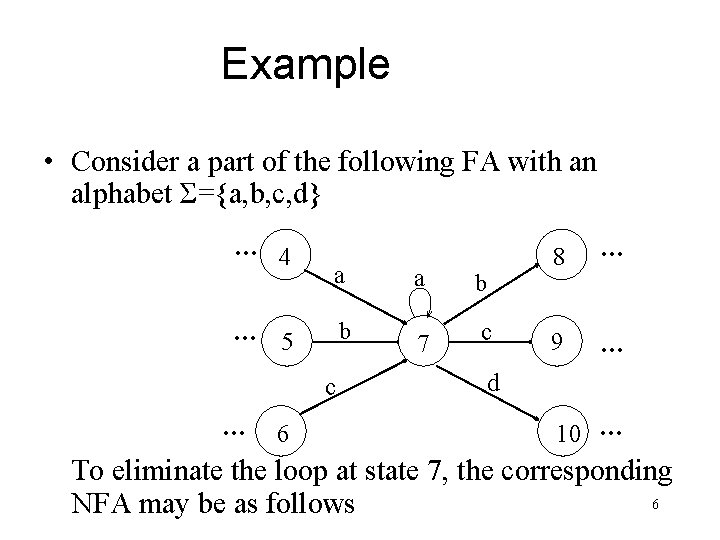
Example • Consider a part of the following FA with an alphabet Σ={a, b, c, d} … 4 a b … 5 c … 6 a 7 b c 8 … 9 … d 10 … To eliminate the loop at state 7, the corresponding 6 NFA may be as follows

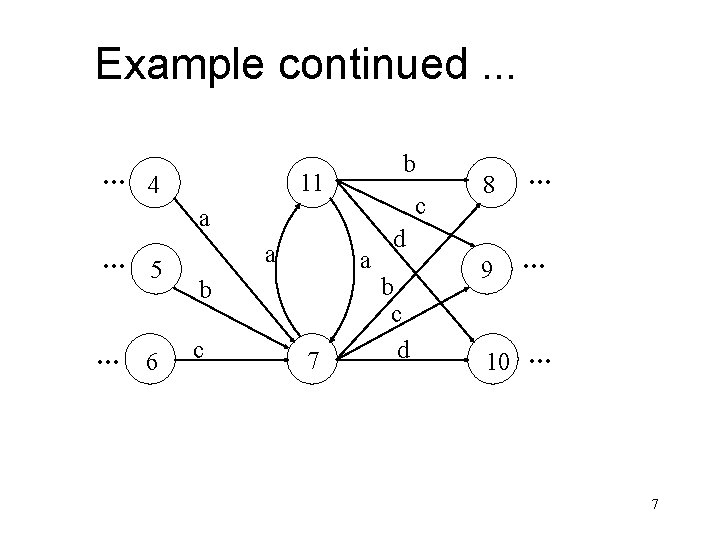
Example continued. . . … 4 b 11 c a … 5 … 6 a a b c 7 8 … 9 … d b c d 10 … 7

Converting an FA to an equivalent NFA • It is to be noted that according to the Kleene’s theorem, if a language can be accepted by an FA, then there exists a TG accepting that language. Since, an NFA is a TG as well, therefore there exists an NFA accepting the language accepted by the given FA. In this case these FA and NFA are said to be equivalent to each others. Following are the examples of FAs to be converted to the equivalent NFAs 8

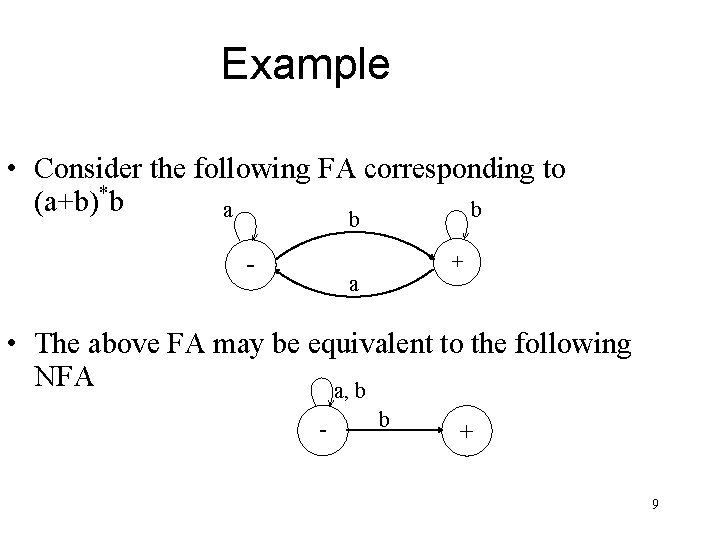
Example • Consider the following FA corresponding to (a+b)*b a b b - + a • The above FA may be equivalent to the following NFA a, b - b + 9

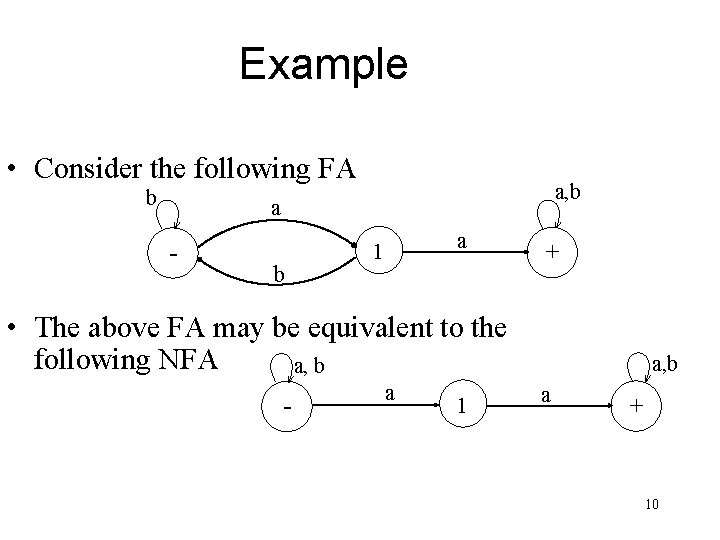
Example • Consider the following FA b a, b a - b a 1 + • The above FA may be equivalent to the following NFA a, b - a 1 a, b a + 10

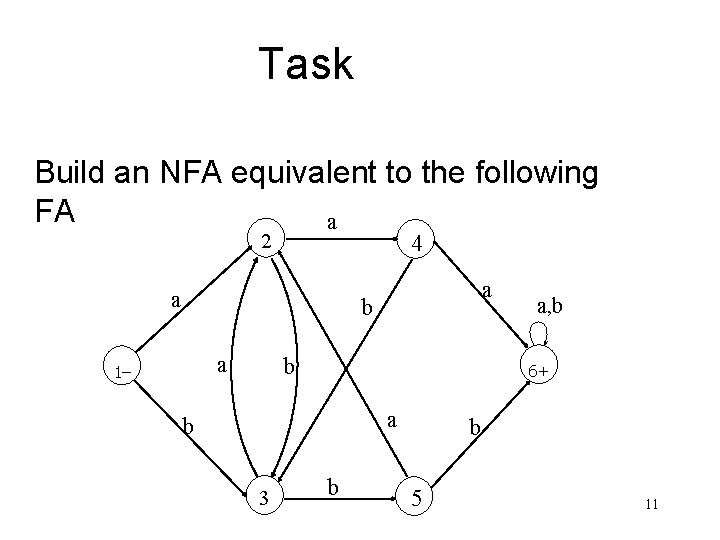
Task Build an NFA equivalent to the following FA a 2 4 a a b a 1– b 6+ a b 3 a, b b b 5 11

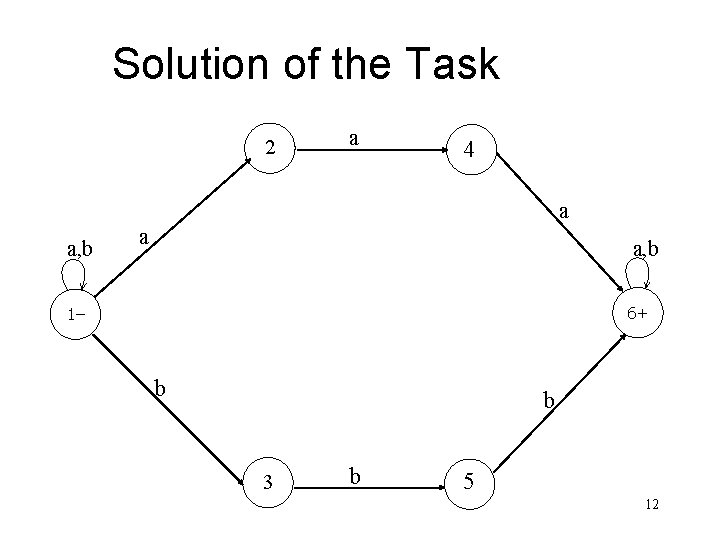
Solution of the Task 2 a 4 a a, b 6+ 1– b b 3 b 5 12

Note • It is to be noted that every FA can be considered to be an NFA as well , but the converse may not true. • It may also be noted that every NFA can be considered to be a TG as well, but the converse may not true. It may be observed that if the transition of null string is also allowed at any state of an NFA then what will be the behavior in the new structure. This structure is defined in the 13 following

NFA with Null String Definition: If in an NFA, is allowed to be a label of an edge then the NFA is called NFA with (NFA- ). An NFA- is a collection of three things (1) Finite many states with one initial and some final states. (2) Finite set of input letters, say, ={a, b, c}. (3) Finite set of transitions, showing where to move if a letter is input at certain state. There may be more than one transitions for certain letter and there may not be any transition for a certain letter. The transition of is also allowed at 14 any state.

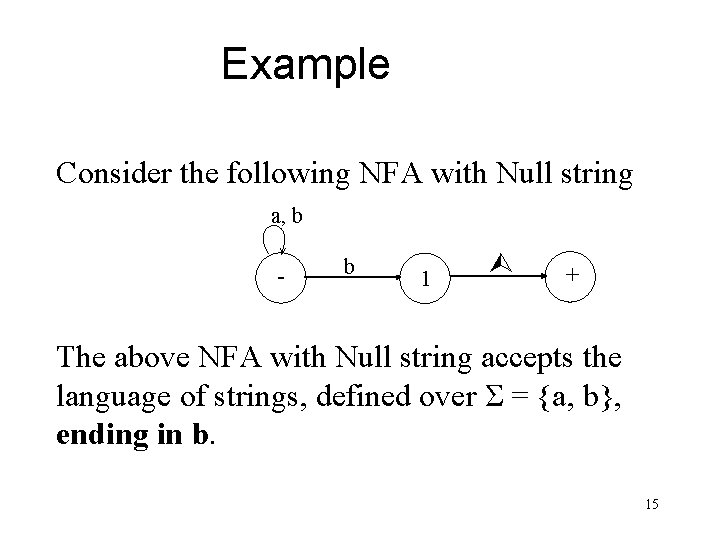
Example Consider the following NFA with Null string a, b - b 1 + The above NFA with Null string accepts the language of strings, defined over Σ = {a, b}, ending in b. 15

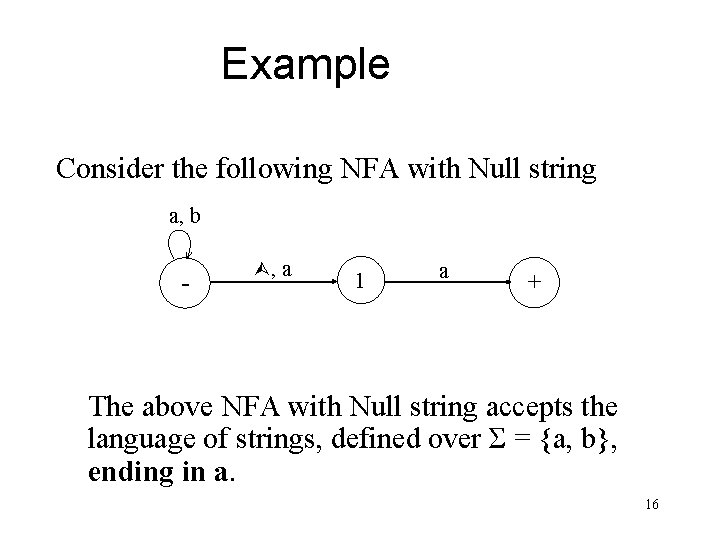
Example Consider the following NFA with Null string a, b - , a 1 a + The above NFA with Null string accepts the language of strings, defined over Σ = {a, b}, ending in a. 16

Note • It is to be noted that every FA may be considered to be an NFA- as well, but the converse may not true. • Similarly every NFA- may be considered to be a TG as well, but the converse may not true. 17

NFA to FA Two methods are discussed in this regard. Method 1: Since an NFA can be considered to be a TG as well, so a RE corresponding to the given NFA can be determined (using Kleene’s theorem). Again using the methods discussed in the proof of Kleene’s theorem, an FA can be built corresponding to that RE. Hence for a given NFA, an FA can be built equivalent to the NFA. Examples have, indirectly, been discussed earlier. 18

NFA to FA continued … Method 2: Since in an NFA, there more than one transition for a certain letter and there may not be any transition for certain letter, so starting from the initial state corresponding to the initial state of given NFA, the transition diagram of the corresponding FA, can be built introducing an empty state for a letter having no transition at certain state and a state corresponding to the combination of states, for a letter having more than one transitions. Following are the examples 19

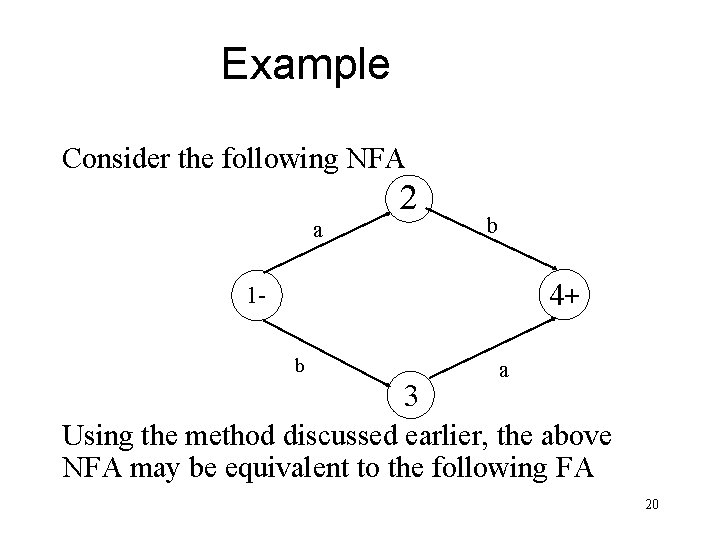
Example Consider the following NFA 2 a b 4+ 1 b 3 a Using the method discussed earlier, the above NFA may be equivalent to the following FA 20

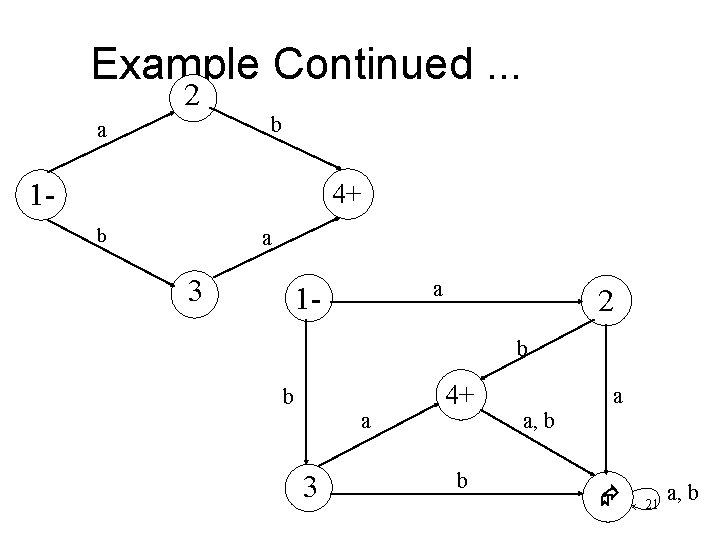
Example Continued. . . 2 b a 1 - 4+ b a 3 a 1 - 2 b b a 3 4+ b a a, b 21 a, b

NFA to FA continued … Method 3: As discussed earlier that in an NFA, there may be more than one transition for a certain letter and there may not be any transition for certain letter, so starting from the initial state corresponding to the initial state of given NFA, the transition table along with new labels of states, of the corresponding FA, can be built introducing an empty state for a letter having no transition at certain state and a state corresponding to the combination of states, for a letter having more than one transitions. 22 Following are the examples

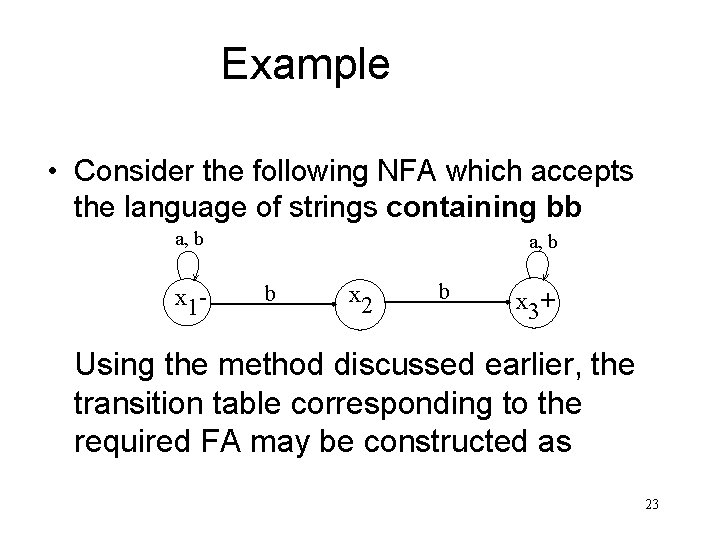
Example • Consider the following NFA which accepts the language of strings containing bb a, b x 1 - a, b b x 2 b x 3+ Using the method discussed earlier, the transition table corresponding to the required FA may be constructed as 23

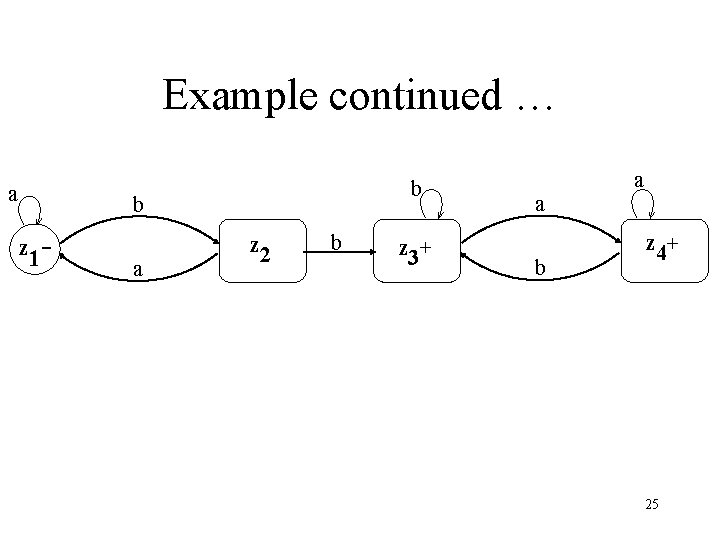
Example continued … Old States New States after reading a b z 1 x 1 z 1 (x 1, x 2) z 2 (x 1, x 2) (x 1 , ) x 1 z 1 (x 1 , x 2, x 3) z 3 (x 1, x 2, x 3) (x 1, x 3) z 4 (x 1 , x 2, x 3) z 3 z 4 (x 1, x 3) z 4 (x 1 , x 2, x 3) z 3 The corresponding transition diagram follows as 24

Example continued … a b b z 1 - a z 2 b z 3+ a b a z 4+ 25

NFA and Kleene’s Theorem It has been discussed that, by Kleene’s theorem part III, there exists an FA corresponding to a given RE. If the given RE is as simple as r=aa+bbb or r=a(a+b)*, the corresponding FAs can easily be constructed. However, for a complicated RE, the RE can be decomposed into simple REs corresponding to which the FAs can easily be constructed and hence, using the method, constructing the FAs corresponding to sum, concatenation and closure of FAs, the required FA can also be constructed. It is to be noted that NFAs also help in proving Kleene’s theorem part III, as well. 26

NFA and Kleene’s Theorem It may be observed that if an NFA can be built corresponding to union, concatenation and closure of FAs corresponding to the REs, then converting the NFA, thus, obtained into an equivalent FA, this FA will correspond to the given RE. Followings are the procedures showing how to obtain NFAs equivalent to union, concatenation and closure of FAs 27

NFA corresponding to Union of FAs Method: Introduce a new start state and connect it with the states originally connected with the old start state with the same transitions as the old start state, then remove the –ve sign of old start state. This creates nondeterminism and hence results in an NFA. 28

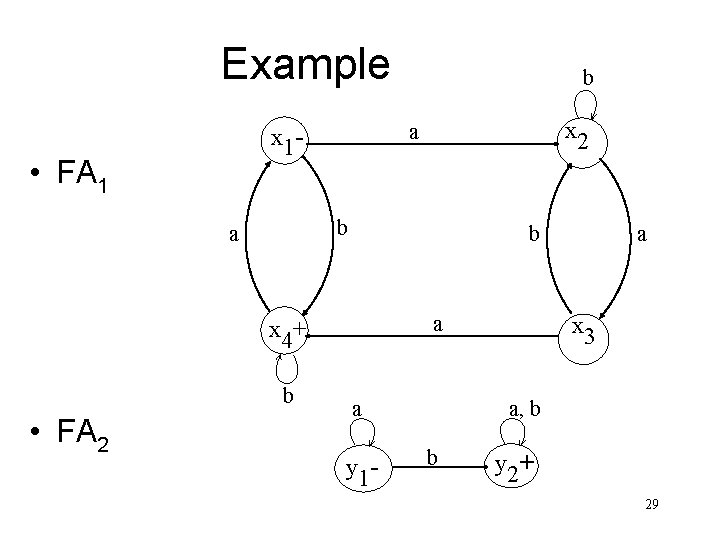
Example b a x 4+ b • FA 2 x 2 a x 1 - • FA 1 b a y 1 - a x 3 a, b b y 2+ 29

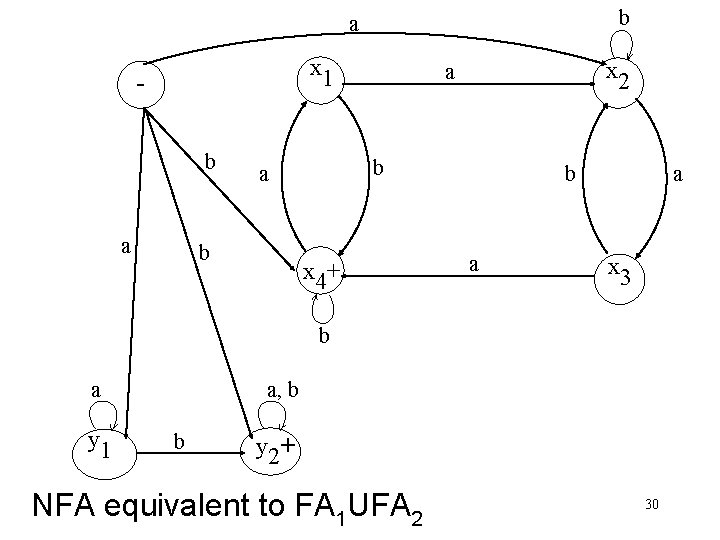
b a x 1 b a b x 2 a x 4+ b a a x 3 b a y 1 a, b b y 2+ NFA equivalent to FA 1 UFA 2 30

Summing Up • converting NFA to FA (method 3), example, NFA and Kleene’s theorem method 1, examples, NFA and Kleene’s theorem method 2 , NFA corresponding to union of FAs, example 31

Summing Up • Examples of Kleene’s theorem part III (method 3), NFA, examples, avoiding loop using NFA, example, converting FA to NFA, examples, applying an NFA on an example of maze 32