Push Down Automata What is a stack A

Push. Down Automata

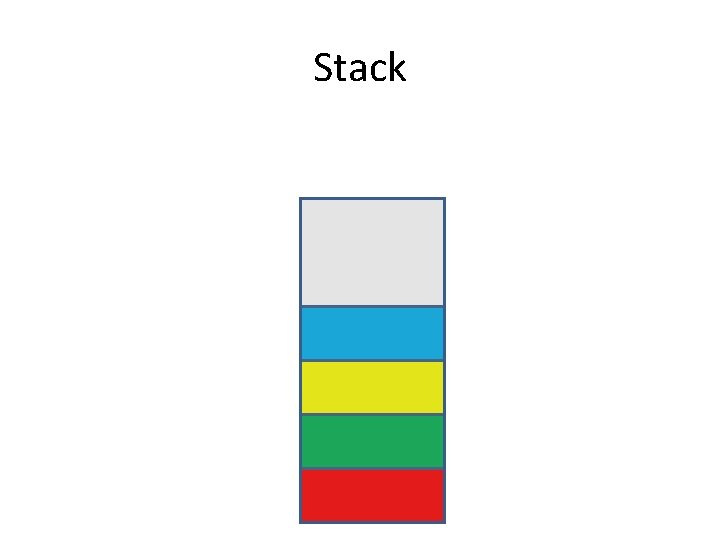
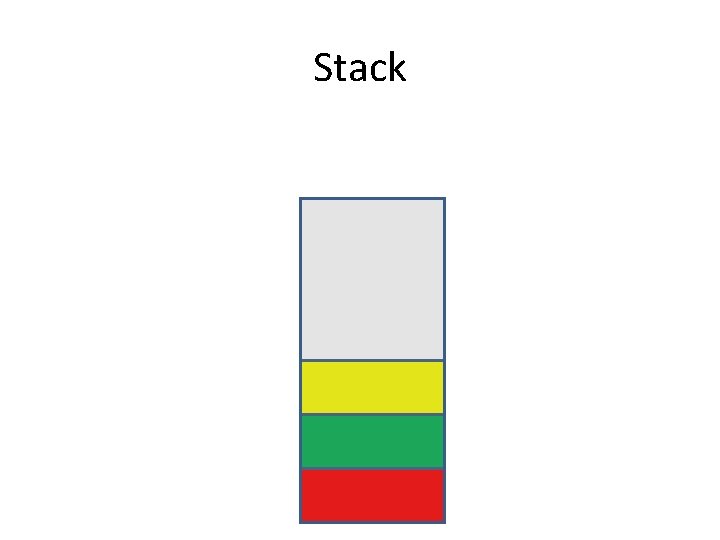
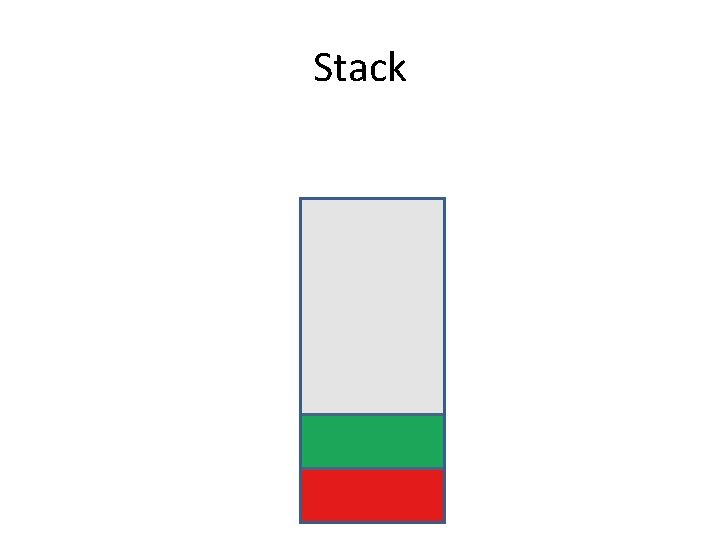
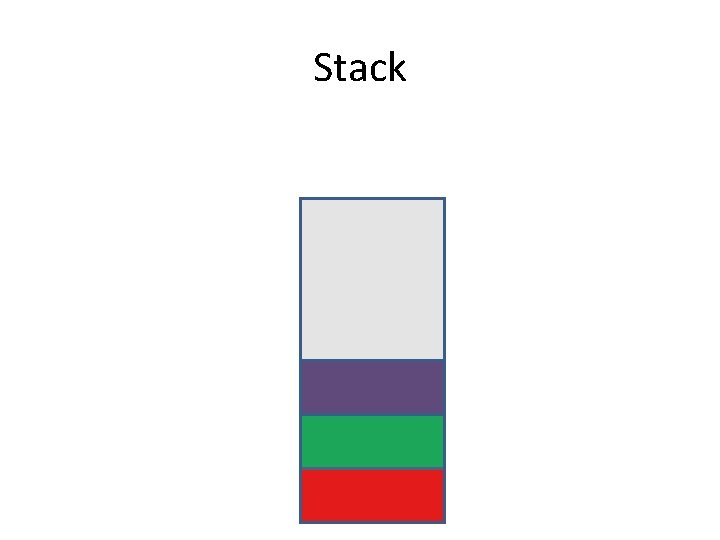
What is a stack? • A stack is a Last In First Out data structure where I only have access to the last element inserted in the stack. • In order to access other elements I have to remove those that are on top one by one.

Stack

Stack

Stack

Stack

Stack

Stack

Stack

Stack

What is a PDA? • A PDA is an enhanced finite automaton that also contains an infinite stack. • The transitions in a PDA are of the form a, x ⟶ y meaning that if you see an a in the input string and the stack contains the symbol x on top then you remove the x and add a y. • The stack gives us extra power to recognize non-regular languages.

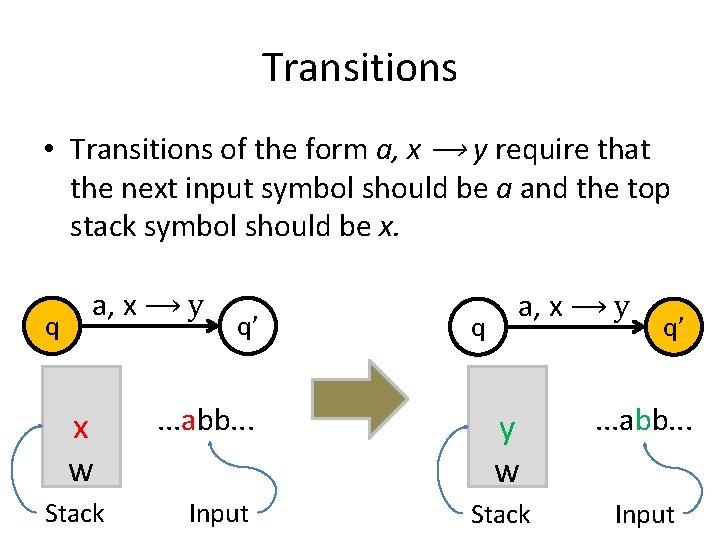
Transitions • Transitions of the form a, x ⟶ y require that the next input symbol should be a and the top stack symbol should be x. q a, x ⟶ y x w Stack q’ . . . abb. . . Input q a, x ⟶ y q’ y w . . . abb. . . Stack Input

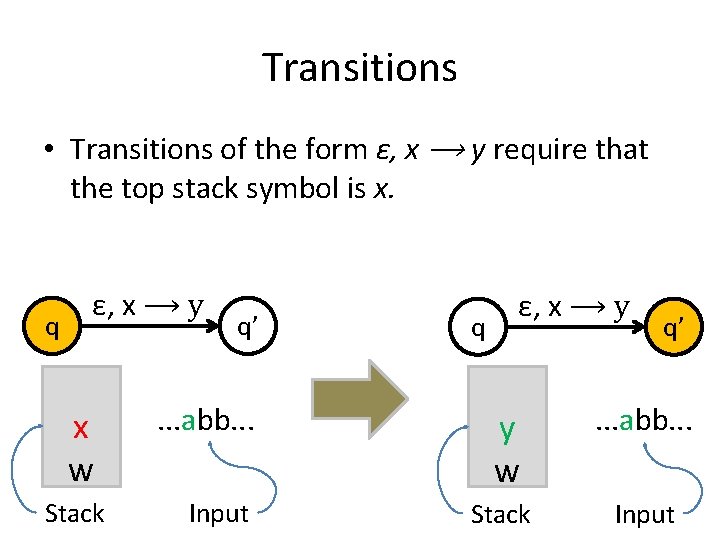
Transitions • Transitions of the form ε, x ⟶ y require that the top stack symbol is x. q ε, x ⟶ y x w Stack q’ . . . abb. . . Input q ε, x ⟶ y q’ y w . . . abb. . . Stack Input

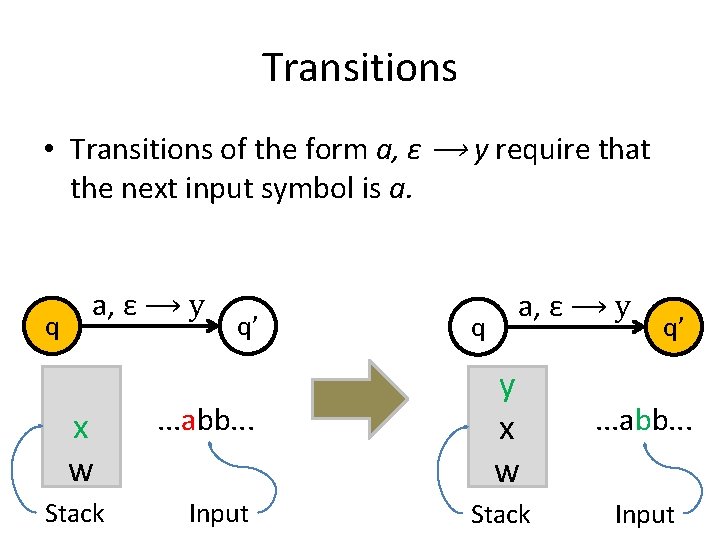
Transitions • Transitions of the form a, ε ⟶ y require that the next input symbol is a. q a, ε ⟶ y x w Stack q’ . . . abb. . . Input q a, ε ⟶ y q’ y x w . . . abb. . . Stack Input

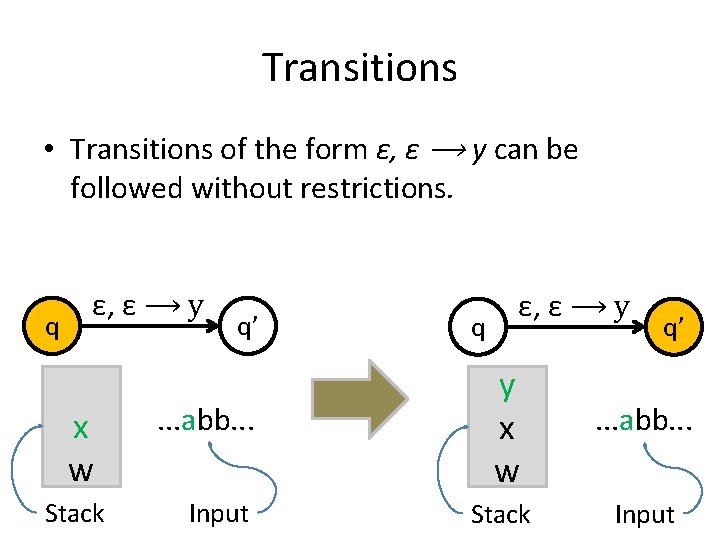
Transitions • Transitions of the form ε, ε ⟶ y can be followed without restrictions. q ε, ε ⟶ y x w Stack q’ . . . abb. . . Input q ε, ε ⟶ y q’ y x w . . . abb. . . Stack Input

PDA Accept – Reject Status • The PDA accepts when there exists a computation path such that: – The computation path ends in an accept state – All the input is consumed – (no requirement for the stack) • The PDA rejects when all the paths: – Either end in a non-accepting state – Or are incomplete (meaning that at some point there is no possible transition under the current input and stack symbols)

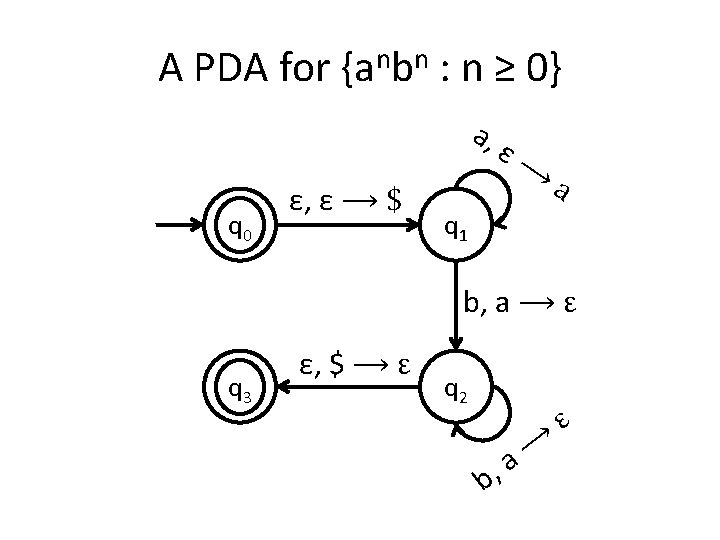
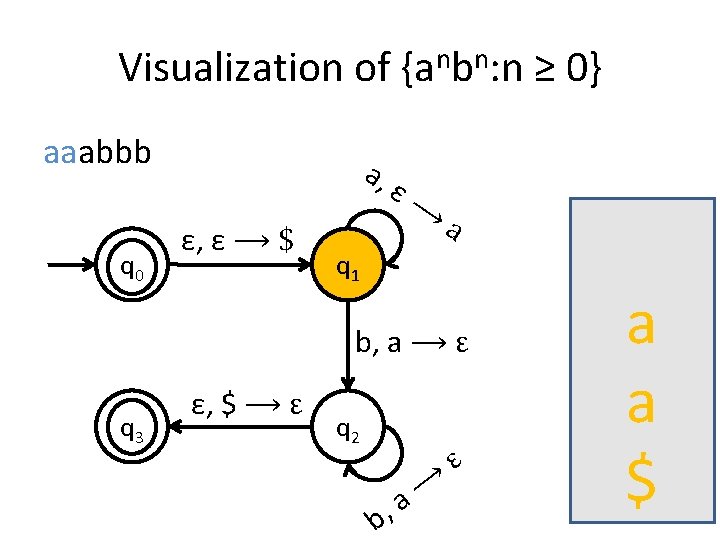
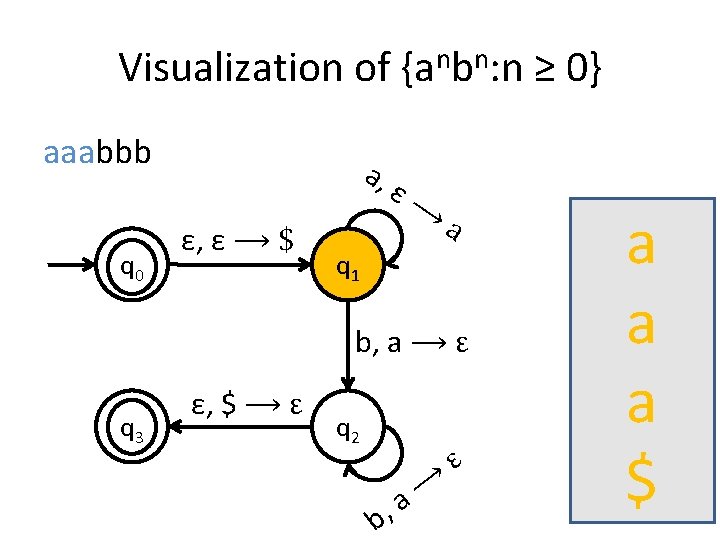
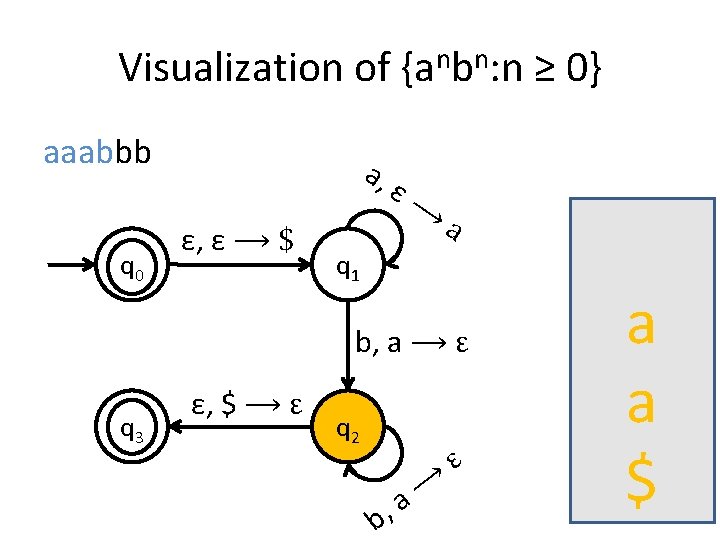
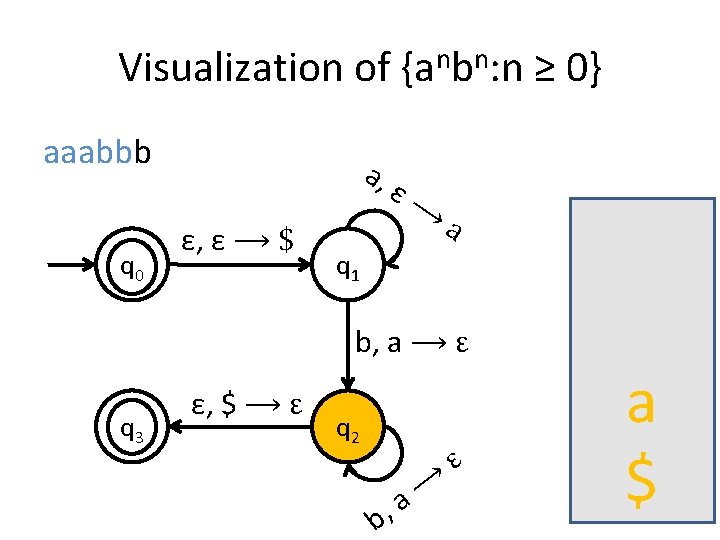
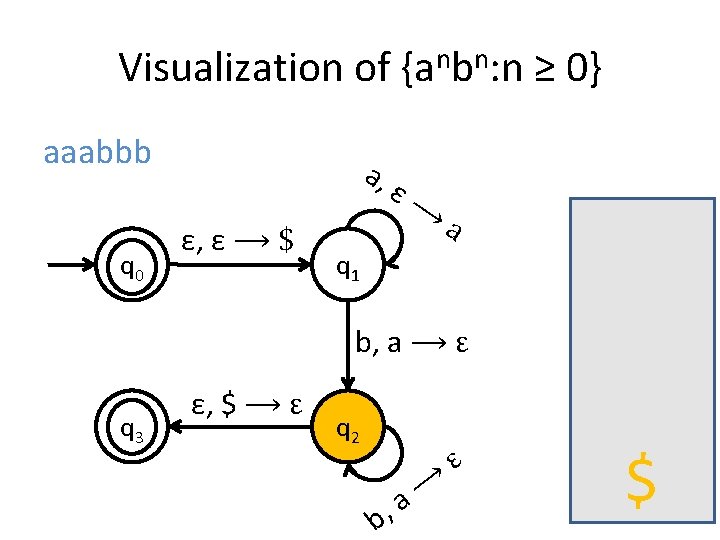
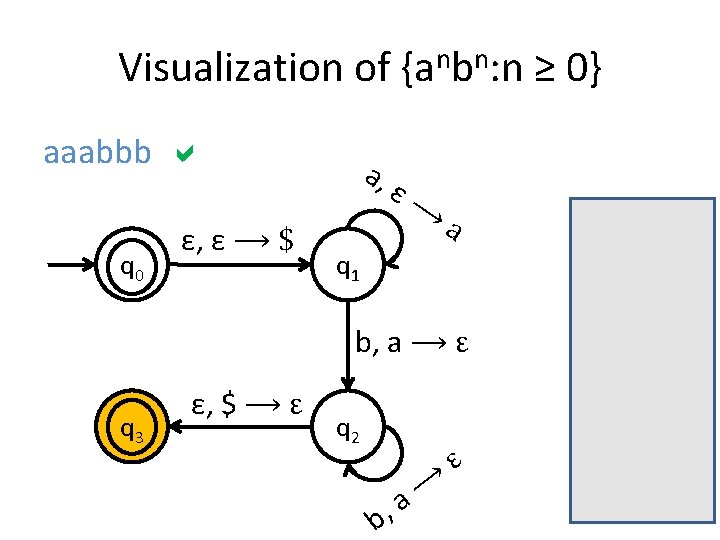
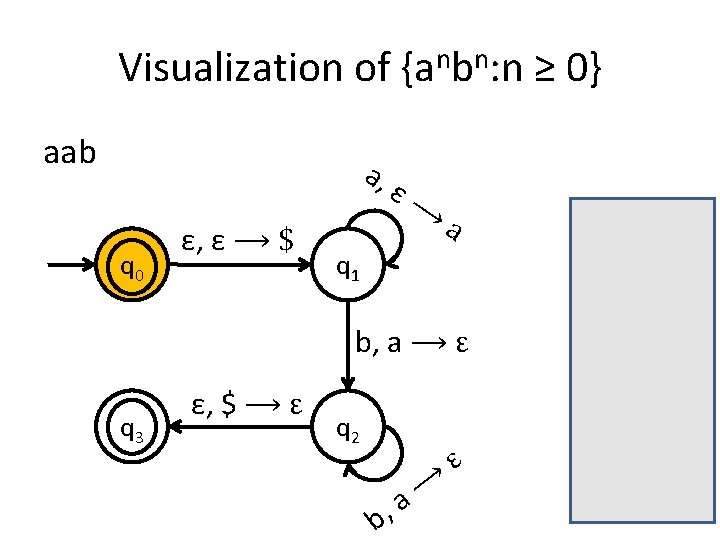
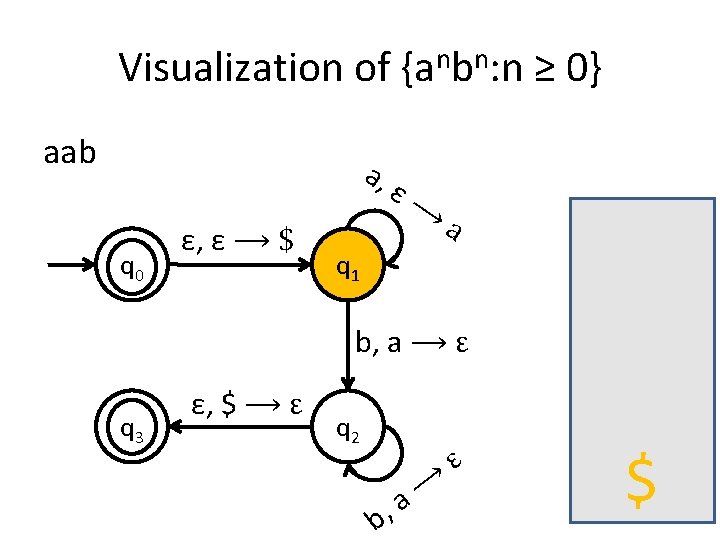
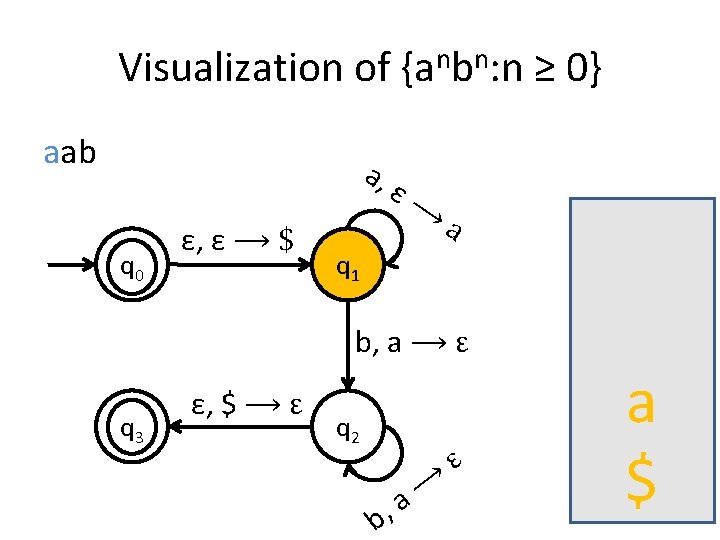
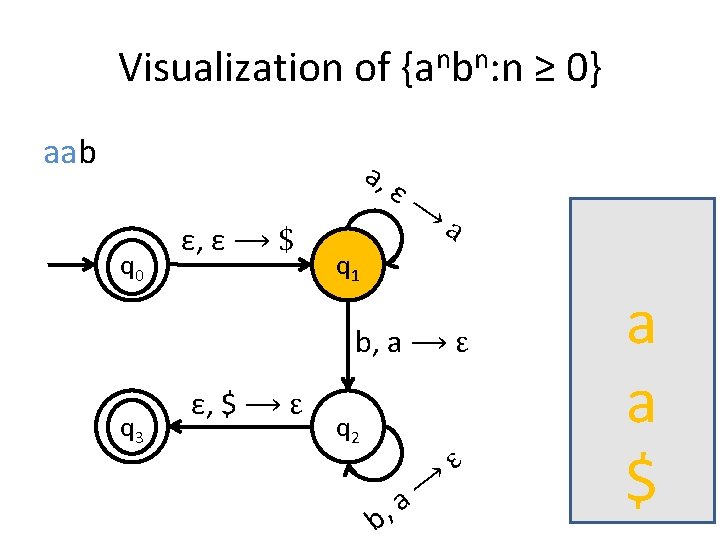
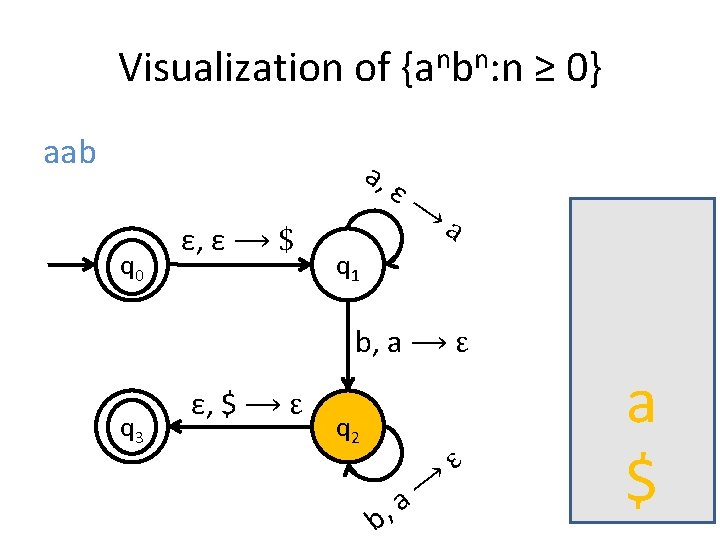
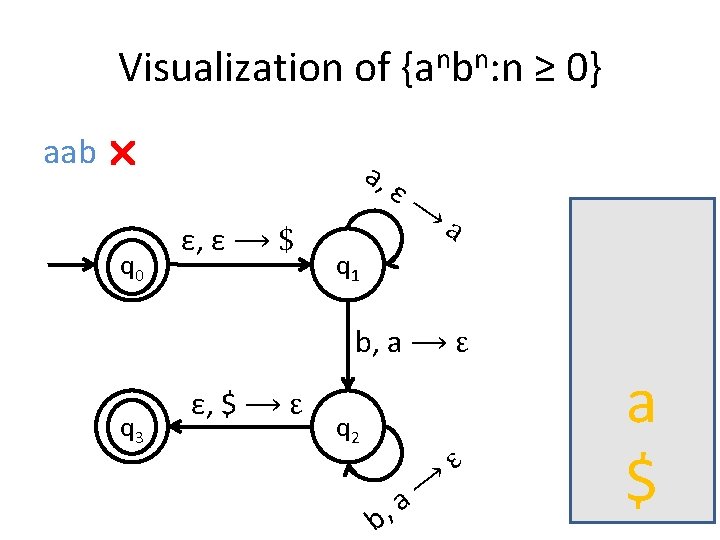
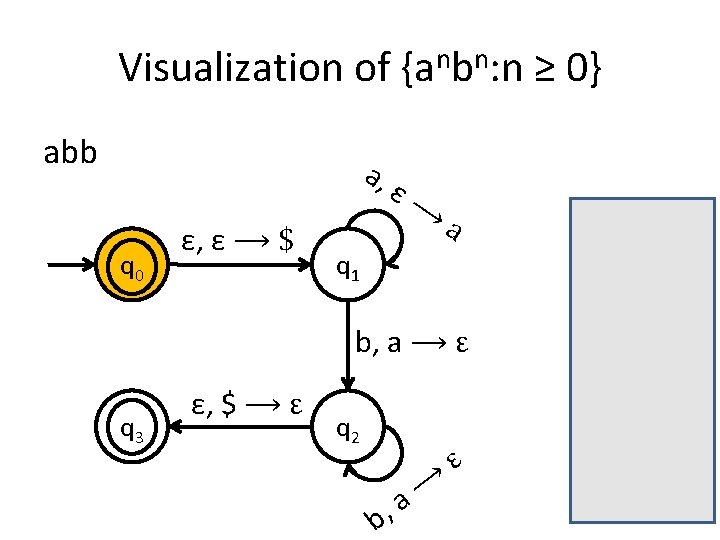
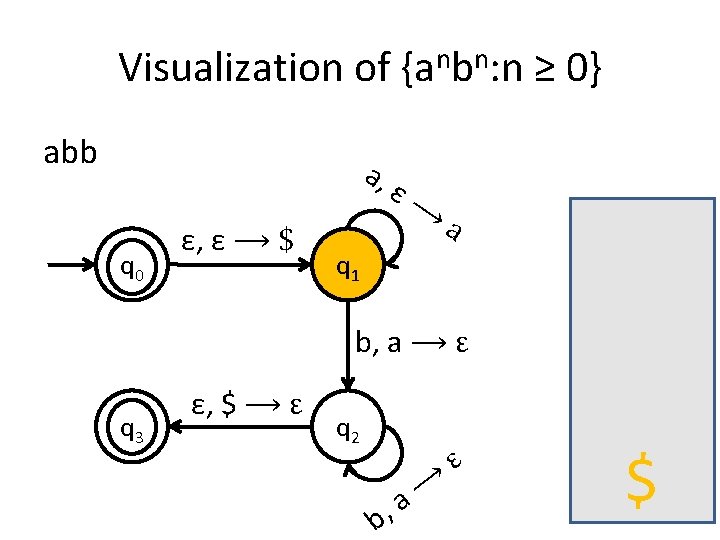
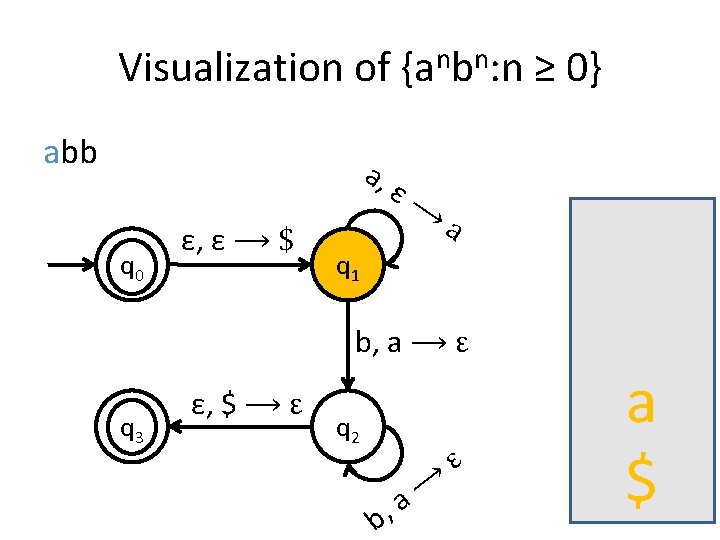
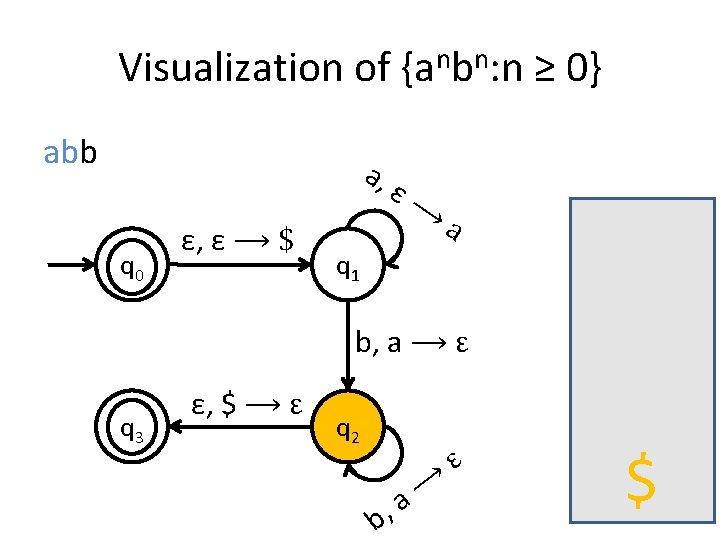
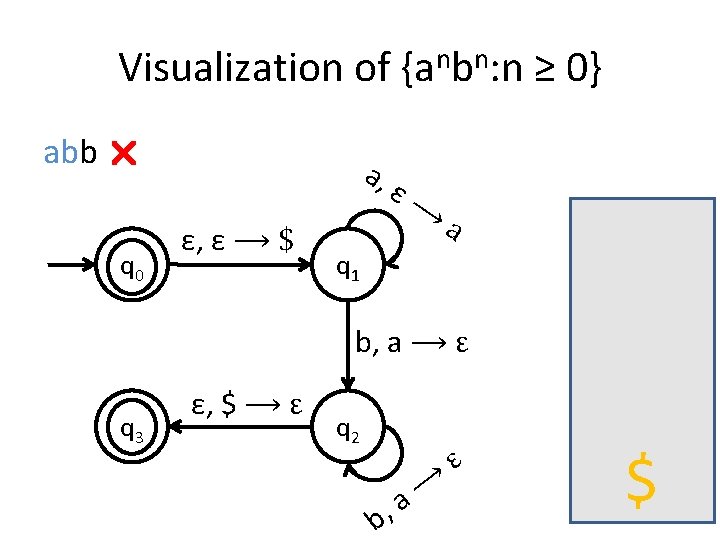
A PDA for {anbn : n ≥ 0} • We usually use the stack for counting. • For this language for example, you first insert all the as in the stack until you start seeing bs. • When you see the first b start removing as from the stack. • When you have consumed the whole string you check the stack: if it’s empty then this means that the number of as equals the number of bs.

Is the stack empty? How can you check if the stack is empty? • What we usually do is to place a special symbol (for example a $) at the bottom of the stack. • Whenever we find the $ again we know that we reached the end of the stack. • In order to accept a string there is no need for the stack to be empty.

Stack push and pop in PDA • a, ε �t when you see an a in the input push t on the stack • a, b �ε when you see an a in the input and b is on the top of the stack, pop b out.

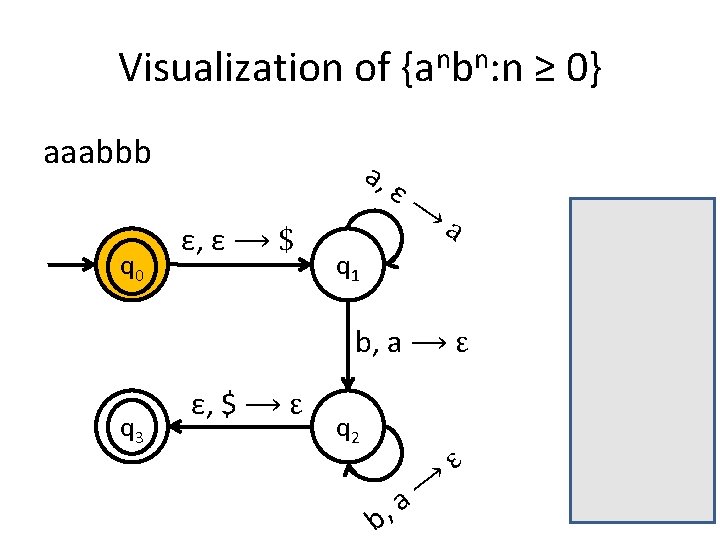
Visualization of {anbn: n ≥ 0} aaabbb q 0 a, ε, ε ⟶ $ ε⟶ a q 1 b, a ⟶ ε q 3 ε, $ ⟶ ε q 2 b, ⟶ a ε

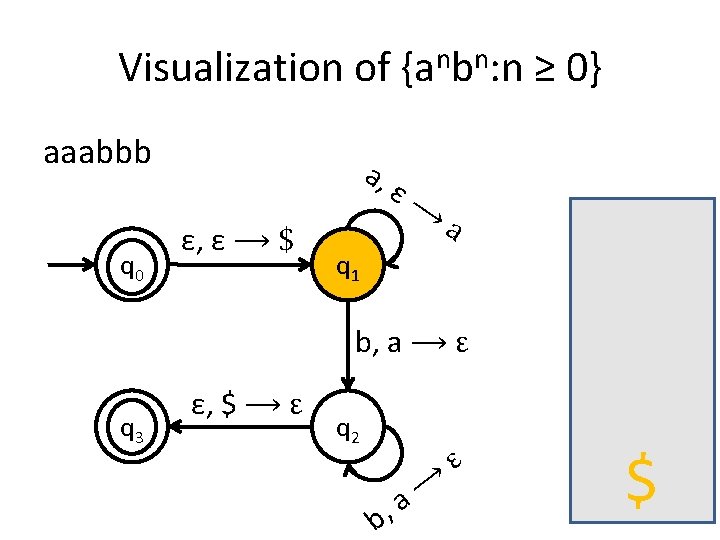
Visualization of {anbn: n ≥ 0} aaabbb q 0 a, ε, ε ⟶ $ ε⟶ a q 1 b, a ⟶ ε q 3 ε, $ ⟶ ε q 2 b, ⟶ a ε $

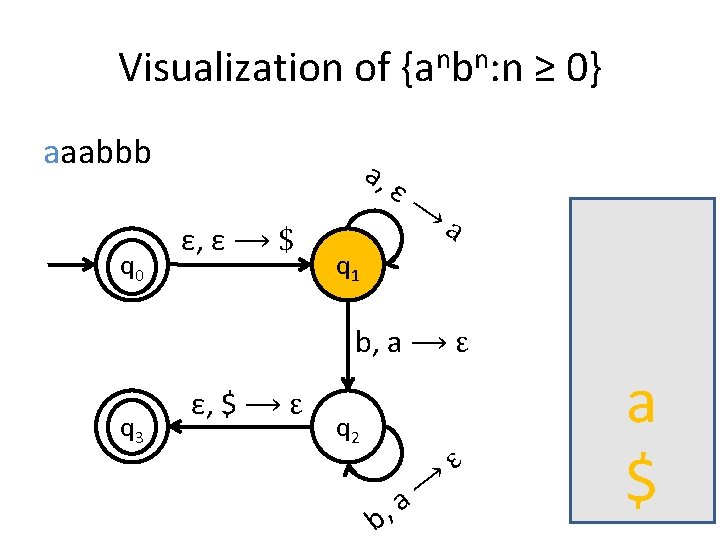
Visualization of {anbn: n ≥ 0} aaabbb q 0 a, ε, ε ⟶ $ ε⟶ a q 1 b, a ⟶ ε q 3 ε, $ ⟶ ε q 2 b, ⟶ a ε a $

Visualization of {anbn: n ≥ 0} aaabbb q 0 a, ε, ε ⟶ $ ε⟶ a q 1 b, a ⟶ ε q 3 ε, $ ⟶ ε q 2 b, ⟶ a ε a a $

Visualization of {anbn: n ≥ 0} aaabbb q 0 a, ε, ε ⟶ $ ε⟶ a q 1 b, a ⟶ ε q 3 ε, $ ⟶ ε q 2 b, ⟶ a ε a a a $

Visualization of {anbn: n ≥ 0} aaabbb q 0 a, ε, ε ⟶ $ ε⟶ a q 1 b, a ⟶ ε q 3 ε, $ ⟶ ε q 2 b, ⟶ a ε a a $

Visualization of {anbn: n ≥ 0} aaabbb q 0 a, ε, ε ⟶ $ ε⟶ a q 1 b, a ⟶ ε q 3 ε, $ ⟶ ε q 2 b, ⟶ a ε a $

Visualization of {anbn: n ≥ 0} aaabbb q 0 a, ε, ε ⟶ $ ε⟶ a q 1 b, a ⟶ ε q 3 ε, $ ⟶ ε q 2 b, ⟶ a ε $

Visualization of {anbn: n ≥ 0} aaabbb q 0 ε, ε ⟶ $ a, ε⟶ a q 1 b, a ⟶ ε q 3 ε, $ ⟶ ε q 2 b, ⟶ a ε

Visualization of {anbn: n ≥ 0} aab a, q 0 ε, ε ⟶ $ ε⟶ a q 1 b, a ⟶ ε q 3 ε, $ ⟶ ε q 2 b, ⟶ a ε

Visualization of {anbn: n ≥ 0} aab a, q 0 ε, ε ⟶ $ ε⟶ a q 1 b, a ⟶ ε q 3 ε, $ ⟶ ε q 2 b, ⟶ a ε $

Visualization of {anbn: n ≥ 0} aab a, q 0 ε, ε ⟶ $ ε⟶ a q 1 b, a ⟶ ε q 3 ε, $ ⟶ ε q 2 b, ⟶ a ε a $

Visualization of {anbn: n ≥ 0} aab a, q 0 ε, ε ⟶ $ ε⟶ a q 1 b, a ⟶ ε q 3 ε, $ ⟶ ε q 2 b, ⟶ a ε a a $

Visualization of {anbn: n ≥ 0} aab a, q 0 ε, ε ⟶ $ ε⟶ a q 1 b, a ⟶ ε q 3 ε, $ ⟶ ε q 2 b, ⟶ a ε a $

Visualization of {anbn: n ≥ 0} aab q 0 a, ε, ε ⟶ $ ε⟶ a q 1 b, a ⟶ ε q 3 ε, $ ⟶ ε q 2 b, ⟶ a ε a $

Visualization of {anbn: n ≥ 0} abb a, q 0 ε, ε ⟶ $ ε⟶ a q 1 b, a ⟶ ε q 3 ε, $ ⟶ ε q 2 b, ⟶ a ε

Visualization of {anbn: n ≥ 0} abb a, q 0 ε, ε ⟶ $ ε⟶ a q 1 b, a ⟶ ε q 3 ε, $ ⟶ ε q 2 b, ⟶ a ε $

Visualization of {anbn: n ≥ 0} abb a, q 0 ε, ε ⟶ $ ε⟶ a q 1 b, a ⟶ ε q 3 ε, $ ⟶ ε q 2 b, ⟶ a ε a $

Visualization of {anbn: n ≥ 0} abb a, q 0 ε, ε ⟶ $ ε⟶ a q 1 b, a ⟶ ε q 3 ε, $ ⟶ ε q 2 b, ⟶ a ε $

Visualization of {anbn: n ≥ 0} abb q 0 a, ε, ε ⟶ $ ε⟶ a q 1 b, a ⟶ ε q 3 ε, $ ⟶ ε q 2 b, ⟶ a ε $

PDA formally • A PDA is a sextuple (Q, Σ, Γ, δ, q 0, F), where: – Q is the set of states – Σ is the input alphabet – Γ is the alphabet for the stack – δ is the transition function – q 0 is the start state – F is the set of accepting states About Γ: The stack alphabet can contain any symbol you want. It can be completely disjoint from Σ.

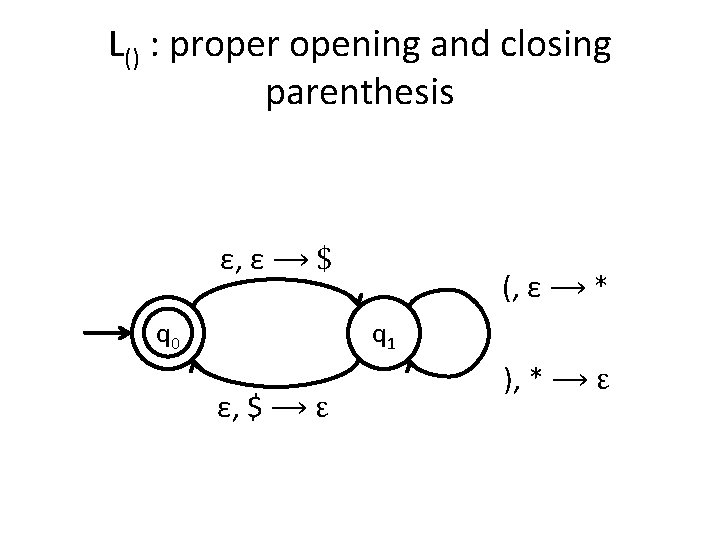
L() : proper opening and closing parenthesis ε, ε ⟶ $ q 0 (, ε ⟶ * q 1 ε, $ ⟶ ε ), * ⟶ ε

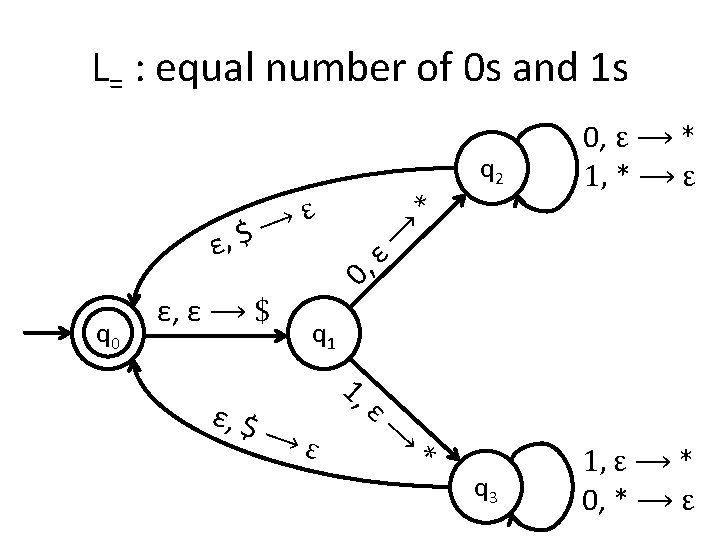
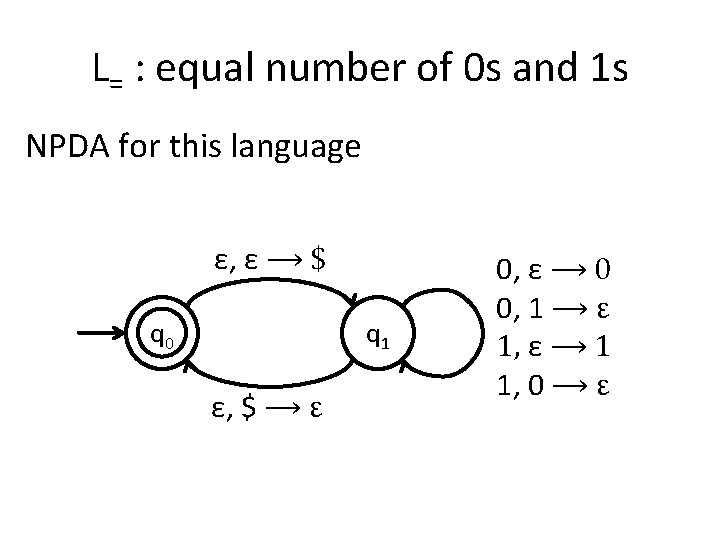
Try it yourself • Create a PDA for the language: L= = {w : w contains an equal number of 0 s and 1 s}

L= : equal number of 0 s and 1 s NPDA for this language ε, ε ⟶ $ q 0 q 1 ε, $ ⟶ ε 0, ε ⟶ 0 0, 1 ⟶ ε 1, ε ⟶ 1 1, 0 ⟶ ε

PDA and Regular Languages • Regular languages can be recognized by PDA: – For every regular language there is an NFAε recognizing it. – Simply add ε⟶ε in every transition for the stack (i. e just don’t use it at all). • The languages recognized by PDA is a superset of regular languages. – As we saw the language L = {anbn : n≥ 0} is recognized by some PDA. – L is not regular.

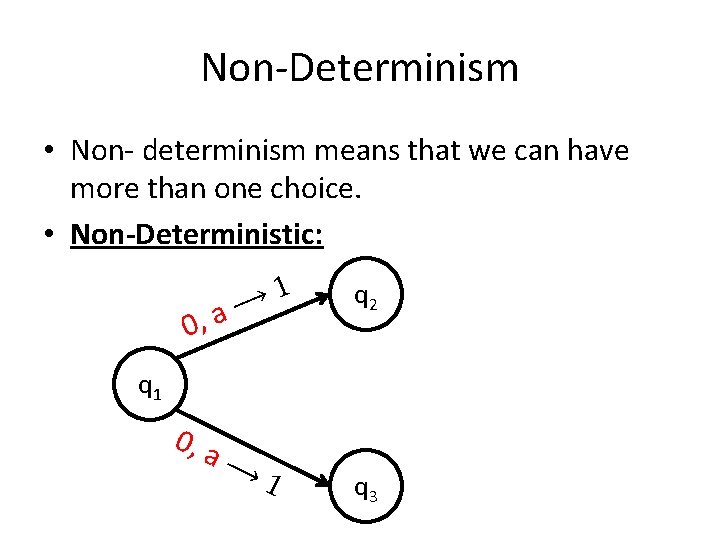
Non-Determinism • Non- determinism means that we can have more than one choice. • Non-Deterministic: ⟶ a , 0 1 q 2 q 1 0, a ⟶ 1 q 3

Non-Determinism • Non- determinism means that we can have more than one choice. • Non-Deterministic: ⟶ a , 0 0 q 2 q 1 0, a ⟶ 1 q 3

Non-Determinism • Non- determinism means that we can have more than one choice. • Non-Deterministic: 0, a ⟶ 0 0, a ⟶ 1 q 2

Non-Determinism • Non- determinism means that we can have more than one choice. • Non-Deterministic: ⟶ ε , 0 0 q 2 q 1 0, a ⟶ 1 q 3

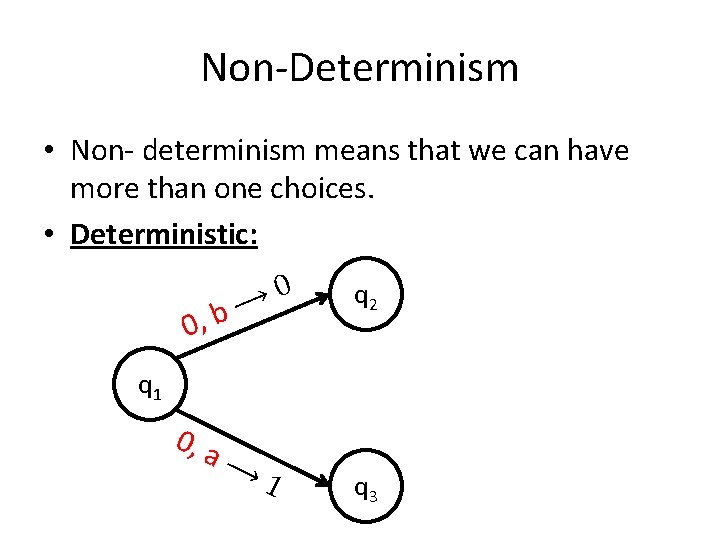
Non-Determinism • Non- determinism means that we can have more than one choices. • Non-Deterministic: ⟶ b , ε 0 q 2 q 1 0, b ⟶ 1 q 3

Non-Determinism • Non- determinism means that we can have more than one choices. • Deterministic: 0 ⟶ b , 0 q 2 q 1 0, a ⟶ 1 q 3

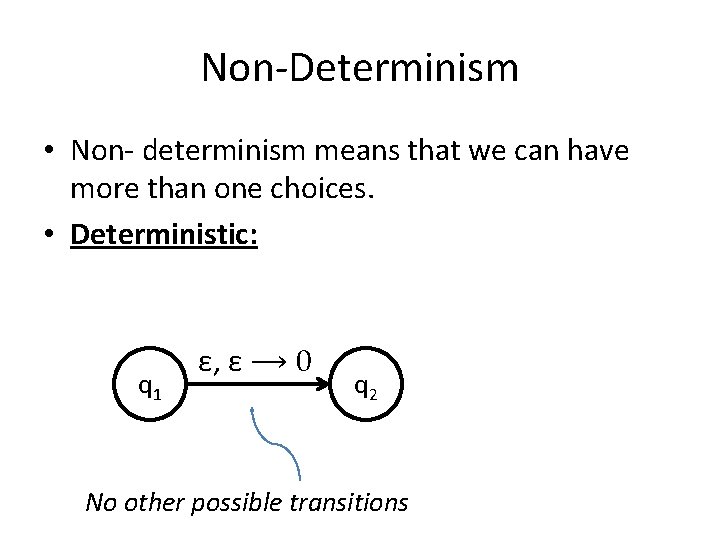
Non-Determinism • Non- determinism means that we can have more than one choices. • Deterministic: q 1 ε, ε ⟶ 0 q 2 No other possible transitions

Definition of DPDA (deterministic push down automata) δ : Q x Σε x Γε (Q x Γε) U {φ} A DPDA has exactly one legal move in every situation where its stack is non empty Given any state q, any letter a, any stack letter x Only one of the following is allowed to be non empty δ(q, a, x) δ(q, a, ε) δ(q, ε, x) δ(q, ε, ε)

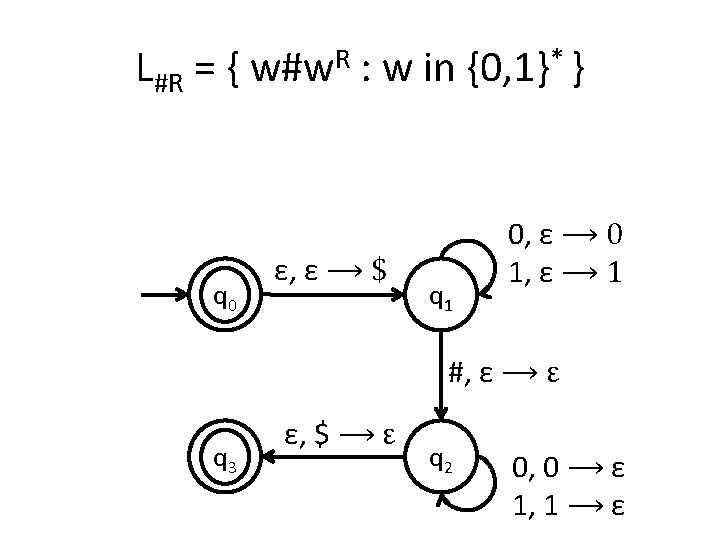
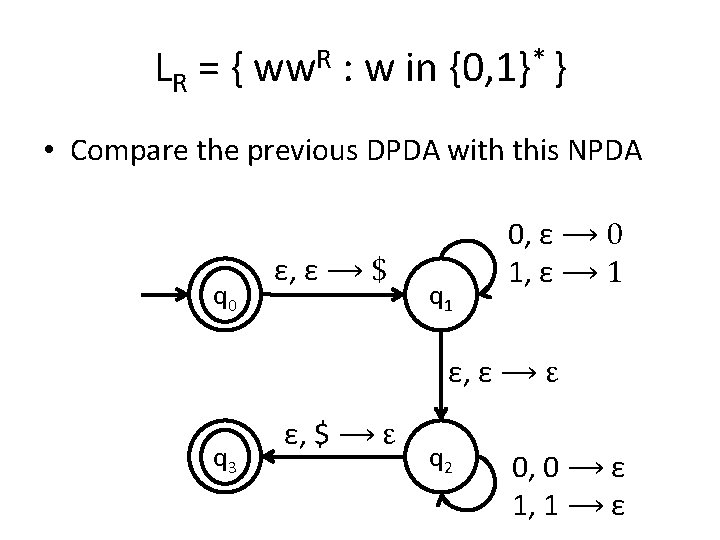
DPDA vs NPDA • Although non-deterministic and deterministic FA are equivalent this is not the case with PDA. Non -determinism helps us recognize more languages. • Intuition: LR = { ww. R : w in {0, 1}* } An NPDA for this language pushes the first half of the string in the stack and pops the second half. It has to guess where the middle of the string is.

LR = { ww. R : w in {0, 1}* } • Compare the previous DPDA with this NPDA q 0 ε, ε ⟶ $ q 1 0, ε ⟶ 0 1, ε ⟶ 1 ε, ε ⟶ ε q 3 ε, $ ⟶ ε q 2 0, 0 ⟶ ε 1, 1 ⟶ ε

NPDA and CF languages • It can be shown that non-deterministic PDA are equivalent with context free grammars. • NPDA accept exactly the set of CF languages. • In order to prove that a language is CF you can – Construct a CF grammar that generates it – Construct a NPDA that recognizes it.