Recap Nondeterministic Finite Automaton NFA A deterministic finite







- Slides: 8

Recap: Nondeterministic Finite Automaton (NFA) A deterministic finite automaton (NFA) is a 5 -tuple (Q, , , s, F) where: • Q is a finite set of elements called states • is a finite input alphabet • : (Q × ( {e})) (Q) • s Q called the start state • F Q called the favorable states Constant! a 1 a 2 …

Acceptance of a Word in an NFA A • Acceptance: w is accepted by A if at least one sequence of transformations yields the empty word and end up in an accepting state • The oracle explanation of NFAs: there is an oracle that always makes the right choice p a r e q Suppose that while processing a w from state r only by going to state p, a favorable state can be reached. Then, the oracle will choose p Oracle will find a path to an accepting state that process all characters only if there is one such path

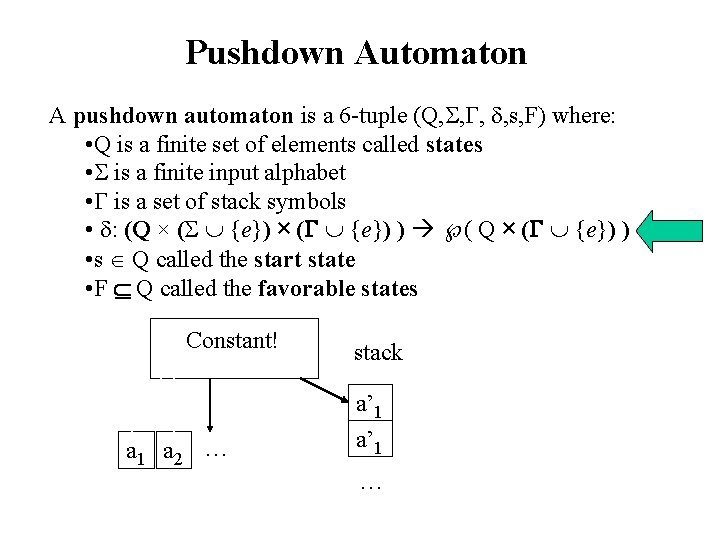
Pushdown Automaton A pushdown automaton is a 6 -tuple (Q, , , , s, F) where: • Q is a finite set of elements called states • is a finite input alphabet • is a set of stack symbols • : (Q × ( {e}) ) ( Q × ( {e}) ) • s Q called the start state • F Q called the favorable states Constant! a 1 a 2 … stack a’ 1 …

Computation in Pushdown Automata PA = (Q, , , , s, F) where: • : (Q × ( {e}) ) ( Q × ( {e}) ) Let (q’, )) ((q, , )), it is compute as follows: if: • the automaton is in an state q • the next character is • The word is on top of the stack Then: • pop from top of the stack • Jump to the state q’ • Push the word on top of the stack

String Accepted by Pushdown Automaton Given a pushdown automaton A, and a string w *, we say that w is accepted by A if there is a sequence of computations that: • begin from the starting state, the word w, and the empty stack • terminates in a favorable state and process all characters in w Ø Note: the stack does not have to be empty at the end The set of all words accepted by an automaton A form the language L(A) accepted or recognized by the automaton.

Example Pushdown automaton recognizing {anbn : n = 0, 1, 2, …}

Example Pushdown automaton recognizing L = {ww. R : w is in *}

Homework for Friday 12. • • • 2. 3 (n), (o) 2. 4 (c) 2. 6 (b) 2. 21 Construct a pushdown automaton for the language of exercise 2. 21