Basics of automata theory Nondeterministic Finite Automata NFA

Basics of automata theory Nondeterministic Finite Automata (NFA) Nondeterministic Finite Automata on infinite words (NFW) 1

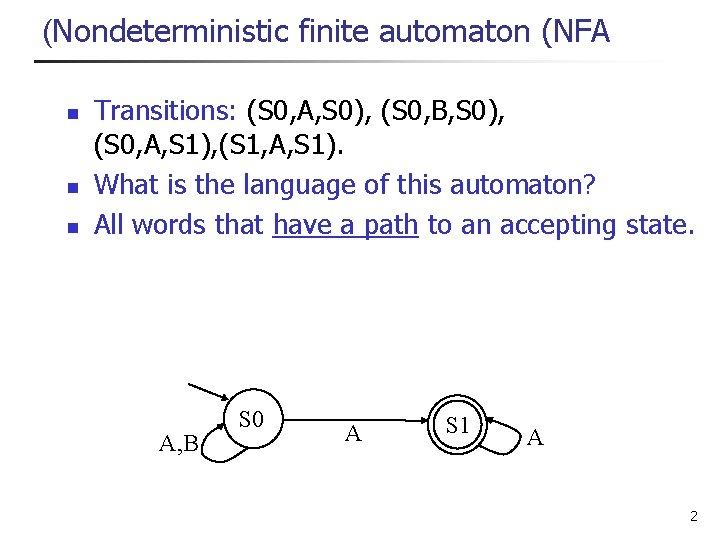
(Nondeterministic finite automaton (NFA n n n Transitions: (S 0, A, S 0), (S 0, B, S 0), (S 0, A, S 1), (S 1, A, S 1). What is the language of this automaton? All words that have a path to an accepting state. A, B S 0 A S 1 A 2

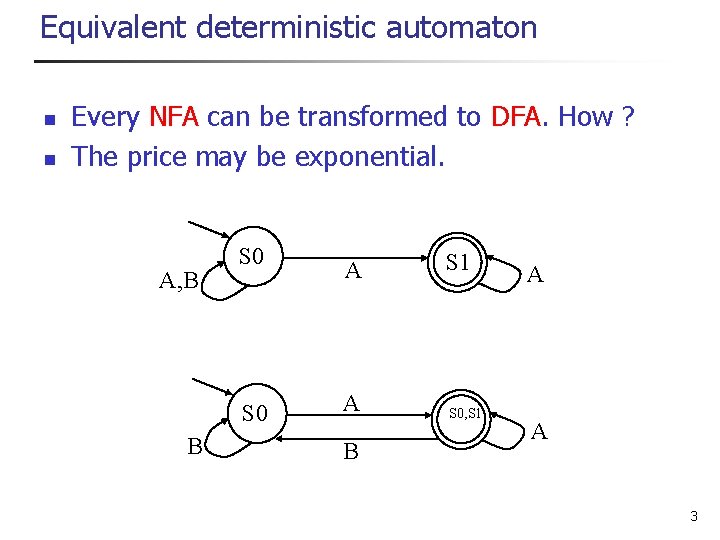
Equivalent deterministic automaton n n Every NFA can be transformed to DFA. How ? The price may be exponential. A, B S 0 B A A B S 1 S 0, S 1 A A 3

Determinization n n Let M = (S, Σ, , I, F) be an NFA. Define a DFA Md = (Sd, Σd, d, Id, Fd), where n n n Sd = P(S) // power-set of S Σd = Σ Id = I d(q, a) = { (r, a) | r 2 q} for all q 2 Sd, a 2 Σ Fd = {q | q 2 Sd ∧ q ∩ F ≠ ; } 4

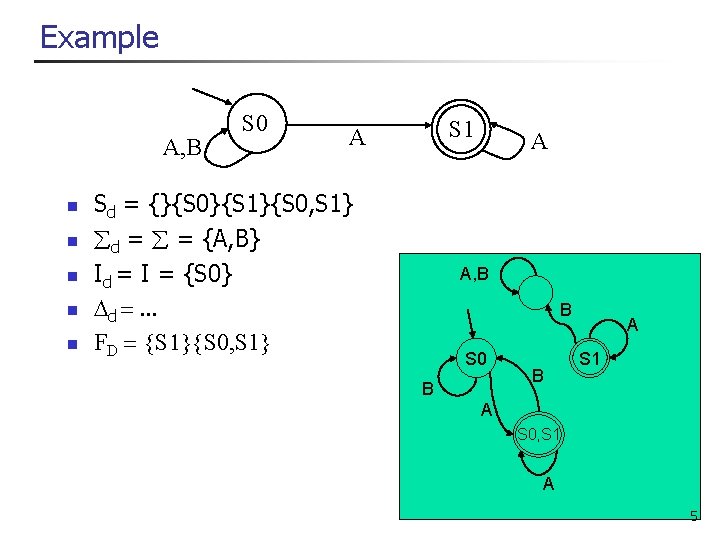
Example A, B n n n S 0 S 1 A Sd = {}{S 0}{S 1}{S 0, S 1} d = = {A, B} Id = I = {S 0} d =. . . FD = {S }{S 0, S 1} A A, B B S 0 B B A S 1 A S 0, S 1 A 5

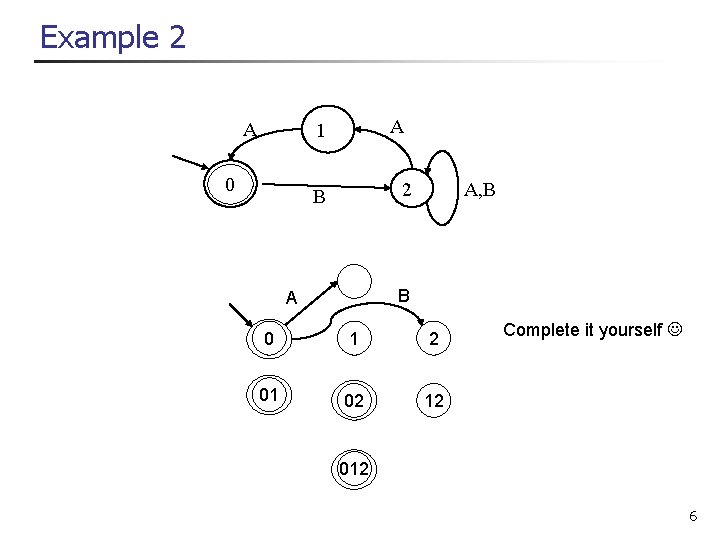
Example 2 A A 1 0 2 B A, B B A 0 1 2 01 02 12 Complete it yourself 012 6

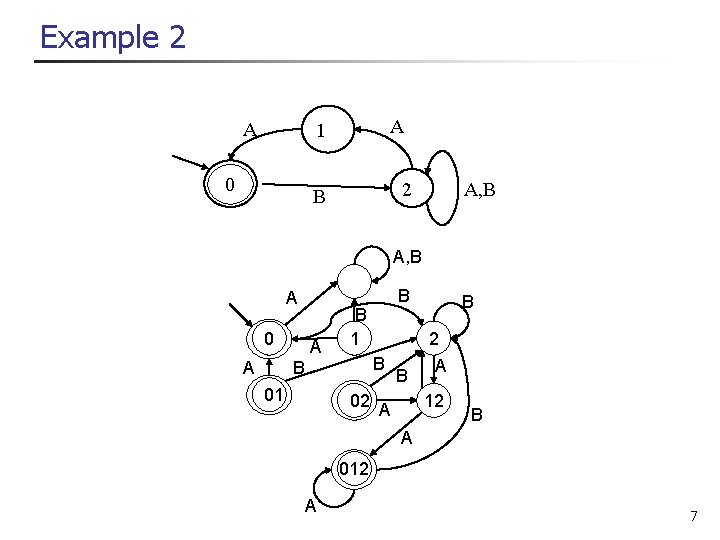
Example 2 A A 1 0 2 B A, B A 0 A A B 1 B 2 B B 01 B B 02 A A 12 B A 012 A 7

Few important questions (1) n n Given two automata A 1, A 2. . . How do we build an automaton A 3 such that L(A 3) = L(A 1) Å L(A 2) n A method to build A 3: compute the product A 1 £ A 2 n We already saw how to compute a product. . . 8

Product of two NFA-s (finite words) Reminder n A 1=h , S 1, , I 1, F 1 i and A 2= h , S 2, I 2, F 2 i n A 1 £ A 2 = n Each state is a pair (s, t): s 2 S 1 and t 2 S 2. n Initial states: pairs (s, t) such that s 2 I 1 and t 2 I 2. n Accepting states: pairs (s, t) such that s 2 F 1 and t 2 F 2 n ((s, t) a (s’, t’)) is a transition if (s, a, s’) 2 1, and (t, a, t’) 2 2. 9

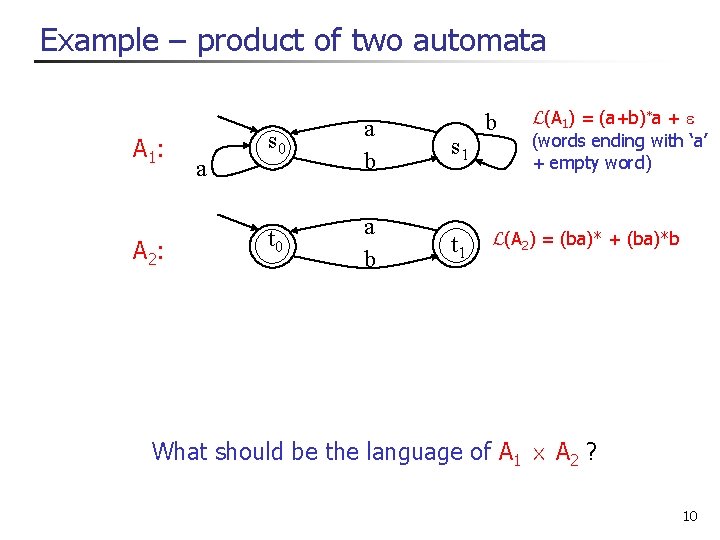
Example – product of two automata A 1: A 2: a s 0 a b s 1 t 0 a b t 1 b L(A 1) = (a+b)*a + (words ending with ‘a’ + empty word) L(A 2) = (ba)* + (ba)*b What should be the language of A 1 £ A 2 ? 10

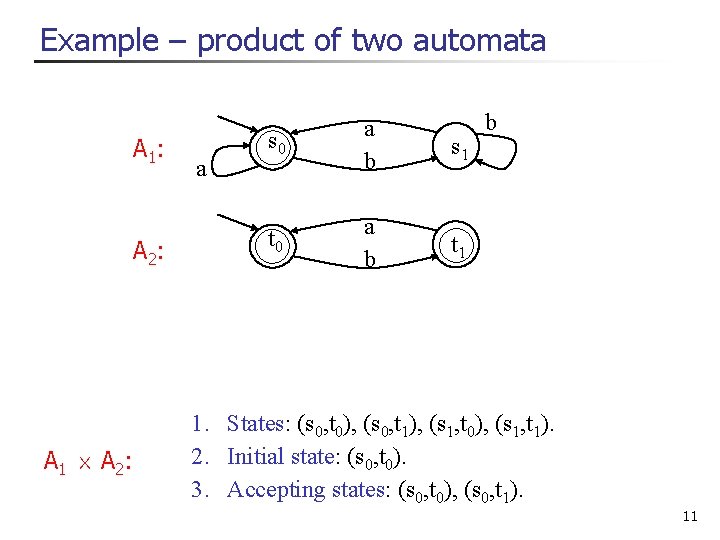
Example – product of two automata A 1: A 2: A 1 £ A 2: a s 0 a b s 1 t 0 a b t 1 b 1. States: (s 0, t 0), (s 0, t 1), (s 1, t 0), (s 1, t 1). 2. Initial state: (s 0, t 0). 3. Accepting states: (s 0, t 0), (s 0, t 1). 11

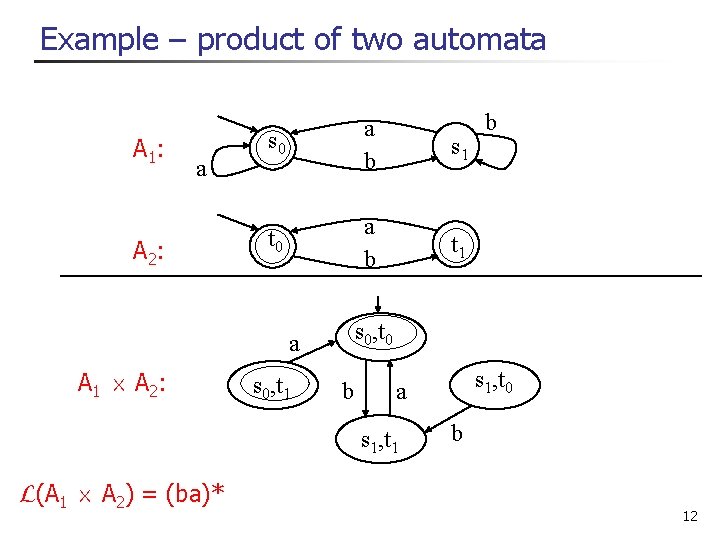
Example – product of two automata A 1: a A 2: s 0 a b s 1 t 0 a b t 1 s 0, t 0 a A 1 £ A 2: s 0, t 1 b s 1, t 0 a s 1, t 1 L(A 1 £ A 2) = (ba)* b b 12

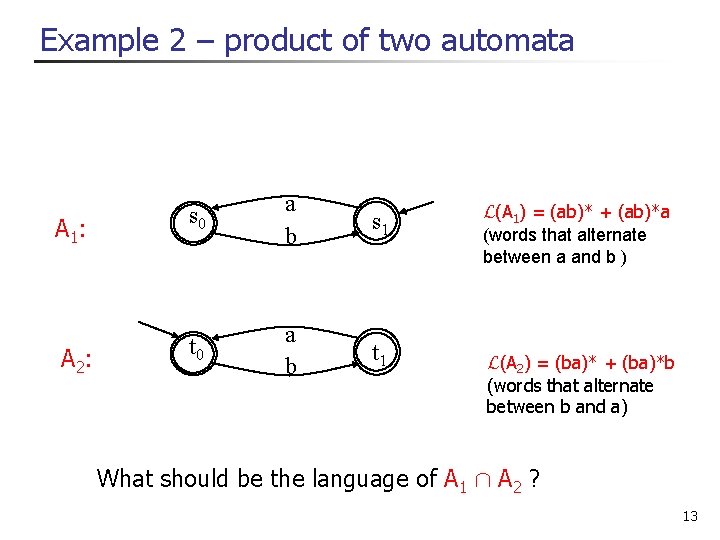
Example 2 – product of two automata A 1: s 0 a b s 1 A 2: t 0 a b t 1 L(A 1) = (ab)* + (ab)*a (words that alternate between a and b ) L(A 2) = (ba)* + (ba)*b (words that alternate between b and a) What should be the language of A 1 Å A 2 ? 13

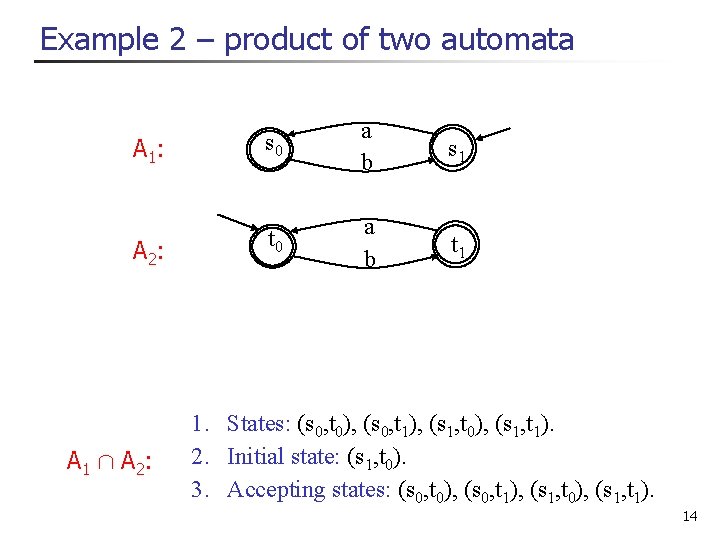
Example 2 – product of two automata A 1: s 0 a b s 1 A 2: t 0 a b t 1 A 1 Å A 2: 1. States: (s 0, t 0), (s 0, t 1), (s 1, t 0), (s 1, t 1). 2. Initial state: (s 1, t 0). 3. Accepting states: (s 0, t 0), (s 0, t 1), (s 1, t 0), (s 1, t 1). 14

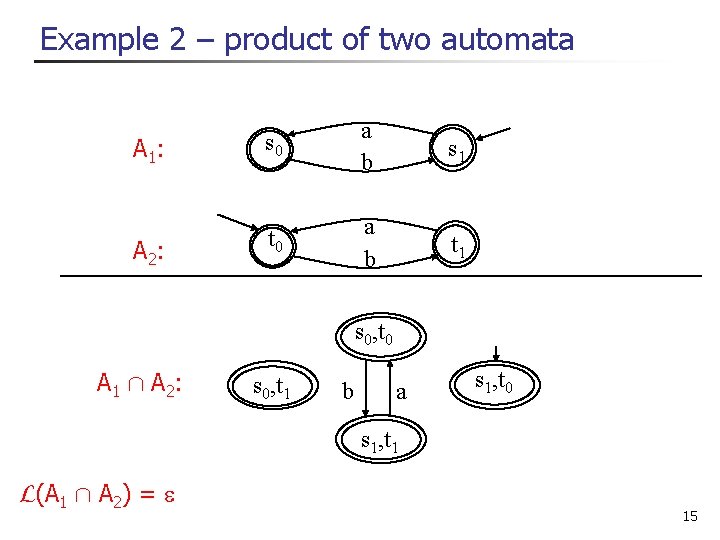
Example 2 – product of two automata A 1: s 0 a b s 1 A 2: t 0 a b t 1 s 0, t 0 A 1 Å A 2: s 0, t 1 b a s 1, t 0 s 1, t 1 L(A 1 Å A 2) = 15

(Few important questions (2 n Given a DFA A: n n n How do we construct A’ such that L(A’) = * - L(A) In other words, how do we build an automaton that accepts exactly those words that are rejected by A ? Answer: compute the complement automaton. n How ? Let F’ = S – F. (i. e. , substitute accepting and non-accepting states. ) 16

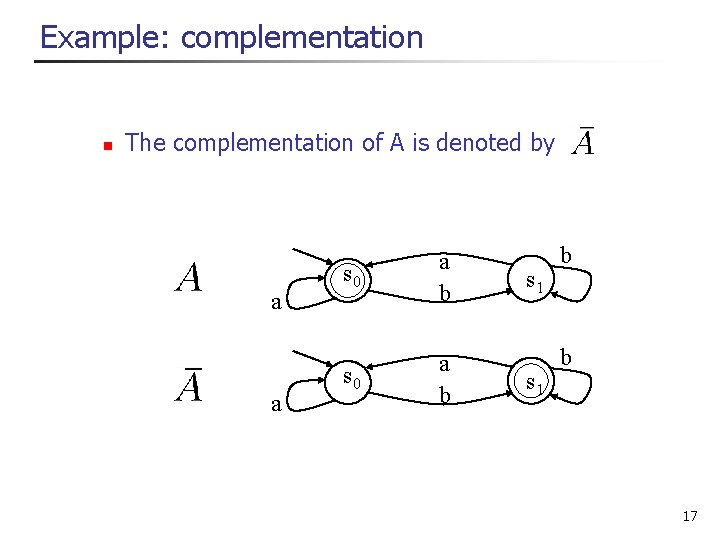
Example: complementation n The complementation of A is denoted by a a s 0 a b s 1 b b 17

(Few important questions (3 n Given an automaton A: n Universality: is L(A) = * ? n Emptiness: is L(A) = ; ? n Emptiness: is an accepting state reachable? n Universality: check whether 18

n And now. . n . . . Automata on infinite words n These are called !-automata 19

Automata over infinite words (DFW / NFW) n n Similar definition. Runs on infinite words over . Accepts when an accepting state occurs infinitely often in the computation. This is called a Buchi automaton a S 0 a b S 1 b 20

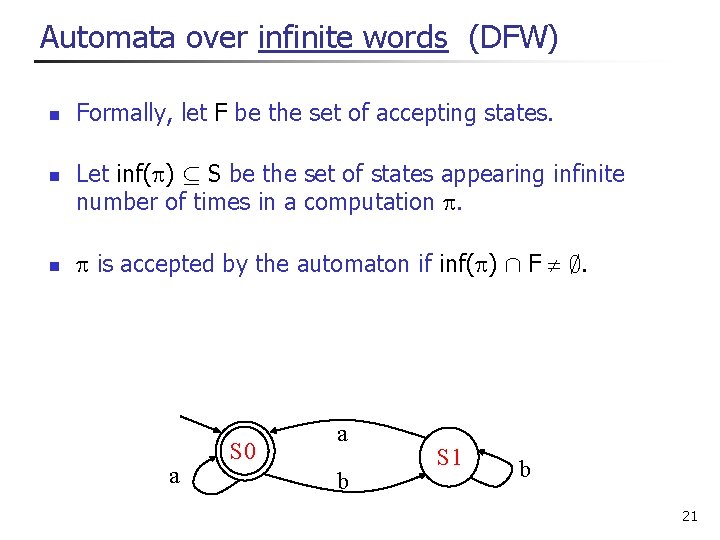
Automata over infinite words (DFW) n n n Formally, let F be the set of accepting states. Let inf( ) µ S be the set of states appearing infinite number of times in a computation . is accepted by the automaton if inf( ) Å F ; . a S 0 a b S 1 b 21

Automata over infinite words (DFW) n Consider the word a b a b… n n The computation is S 0 S 1 … This computation is accepting, since S 0 appears infinitely many times. a S 0 a b S 1 b 22

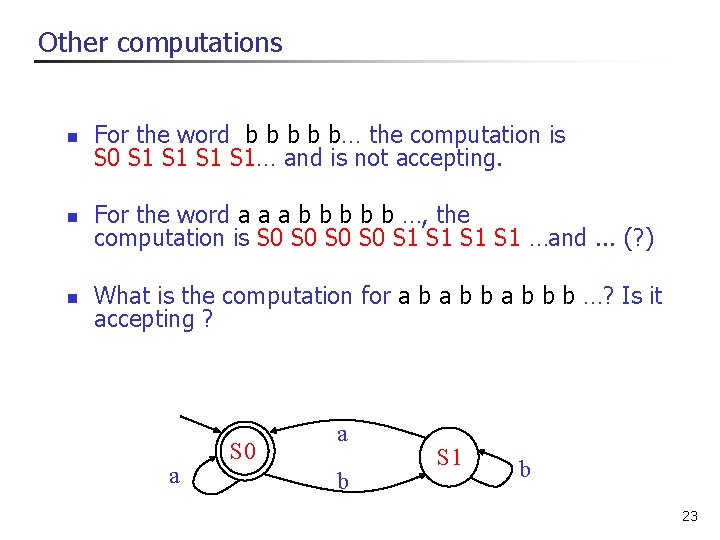
Other computations n For the word b b b… the computation is S 0 S 1 S 1… and is not accepting. n For the word a a a b b b …, the computation is S 0 S 0 S 1 S 1 …and. . . (? ) n What is the computation for a b b b …? Is it accepting ? a S 0 a b S 1 b 23

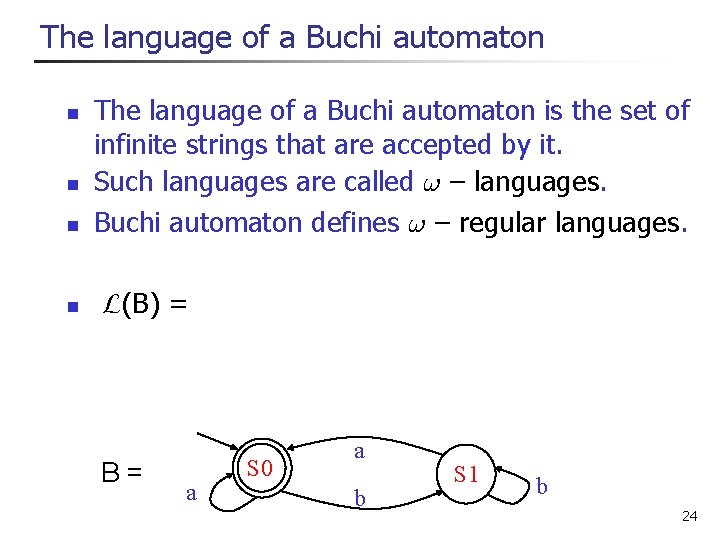
The language of a Buchi automaton n n The language of a Buchi automaton is the set of infinite strings that are accepted by it. Such languages are called ! – languages. Buchi automaton defines ! – regular languages. L(B) = (ab*)! B= a S 0 a b S 1 b 24

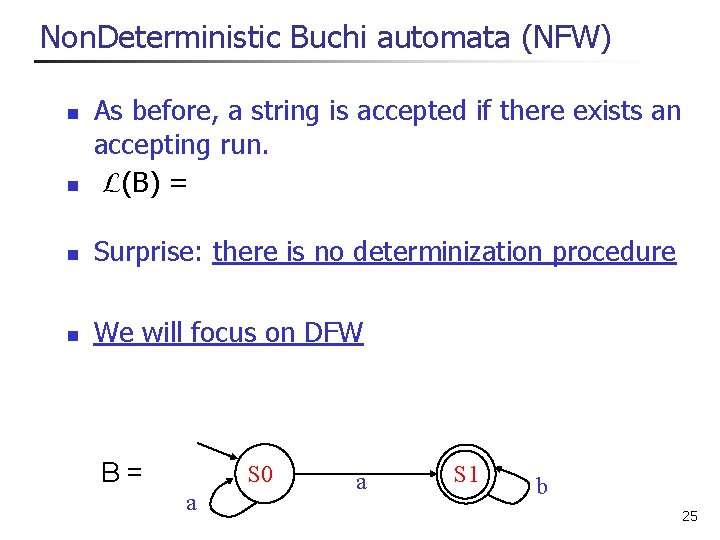
Non. Deterministic Buchi automata (NFW) n As before, a string is accepted if there exists an accepting run. L(B) = aa*b! n Surprise: there is no determinization procedure n We will focus on DFW n B= S 0 a a S 1 b 25

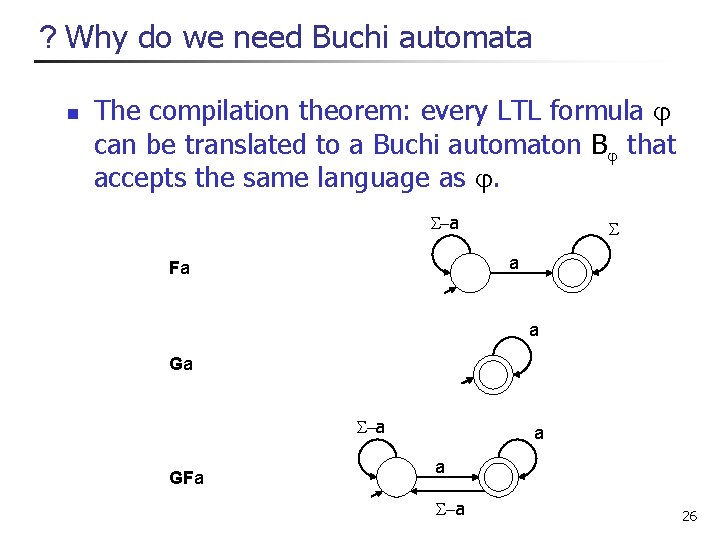
? Why do we need Buchi automata n The compilation theorem: every LTL formula can be translated to a Buchi automaton B that accepts the same language as . -a a Fa a Ga -a GFa a a -a 26

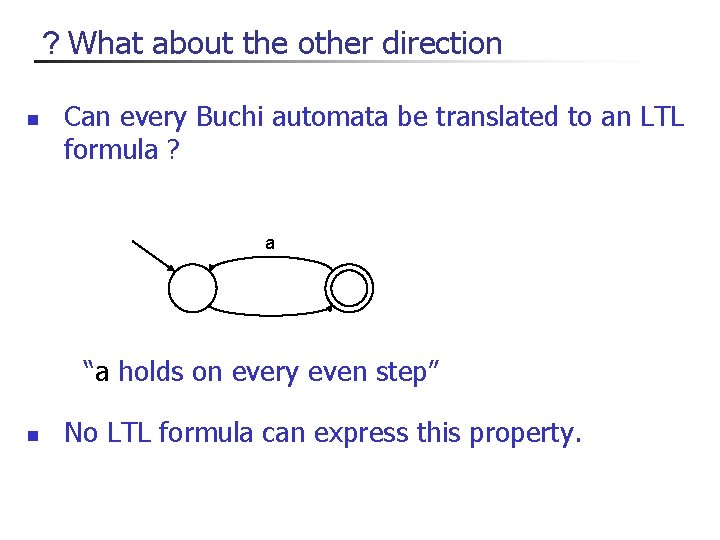
? What about the other direction n Can every Buchi automata be translated to an LTL formula ? a “a holds on every even step” n No LTL formula can express this property.

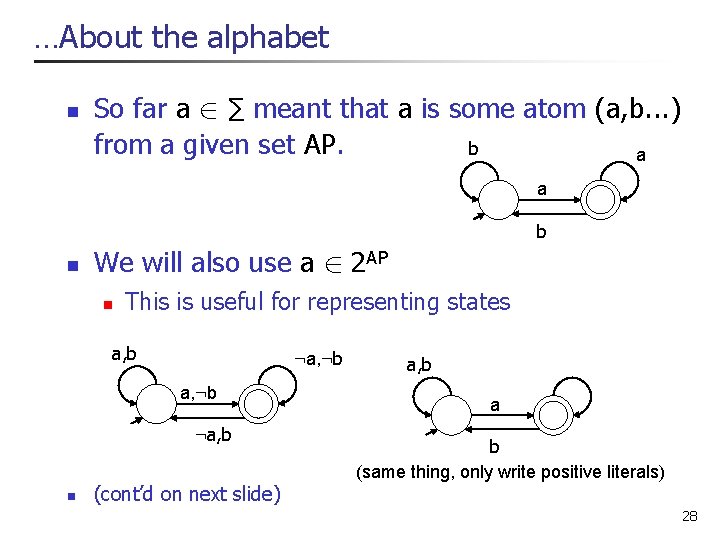
. . . About the alphabet n So far a 2 ∑ meant that a is some atom (a, b. . . ) from a given set AP. b a a b n We will also use a 2 2 AP n This is useful for representing states a, b : a, : b : a, b n (cont’d on next slide) a, b a b (same thing, only write positive literals) 28

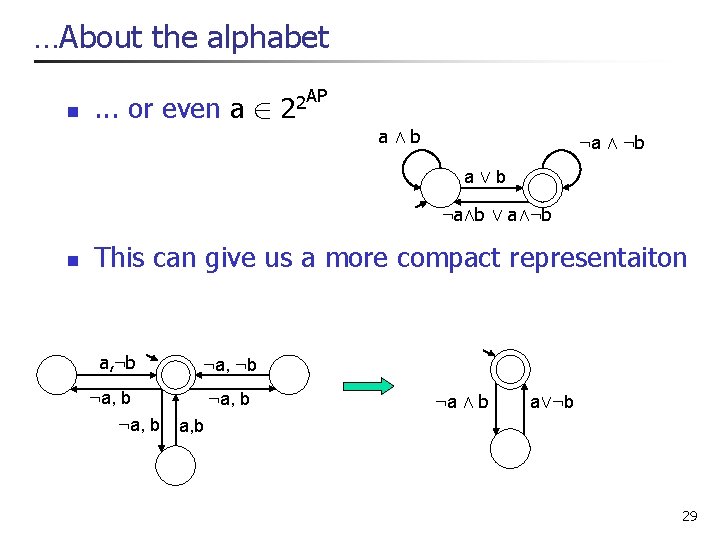
. . . About the alphabet n . . . or even a 2 AP 2 2 aÆb : a Æ : b aÇb : aÆb Ç aÆ: b n This can give us a more compact representaiton a, : b : a, b : a Æ b aÇ: b a, b 29

. . . About the alphabet n n A Buchi automaton can also be represented with labels on states. There is 1 -1 translation to a Buchi automaton with labels on transitions: n Move labels to outgoing edges. 30

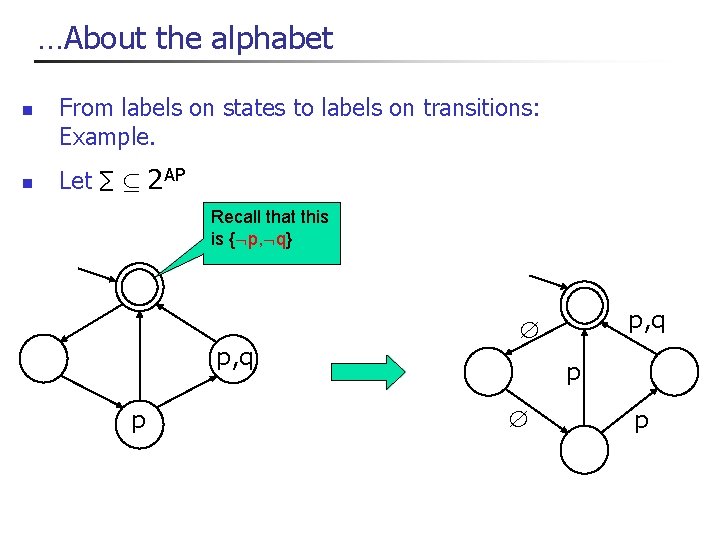
. . . About the alphabet n n From labels on states to labels on transitions: Example. Let ∑ µ 2 AP Recall that this is { p, q} p, q p p, q p p

. . . Again, important questions For Buchi automata B 1, B 2: n How to compute L(B 1) Å L(B 2) ? n How to complement ? n n Find B’ s. t. How to check for emptiness ? n Is L(B) = ; ? 32

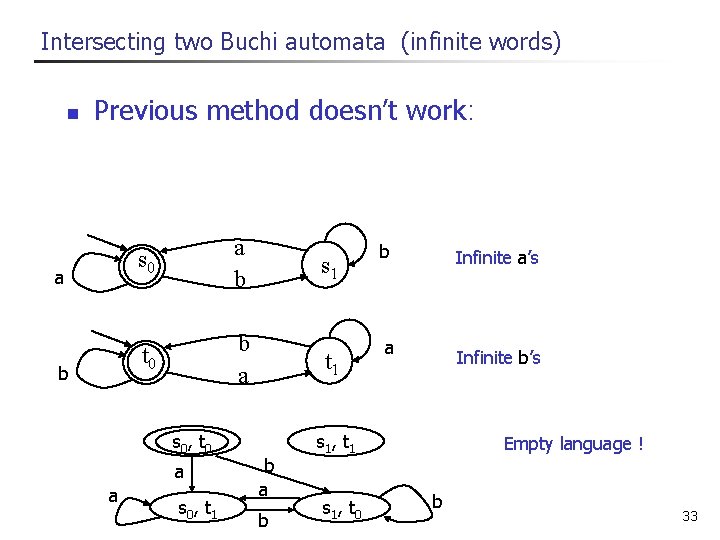
Intersecting two Buchi automata (infinite words) n Previous method doesn’t work: a b s 0 a b t 0 b a s 0 , t 0 a a s 0 , t 1 s 1 t 1 b a b b Infinite a’s a Infinite b’s s 1 , t 1 s 1 , t 0 Empty language ! b 33

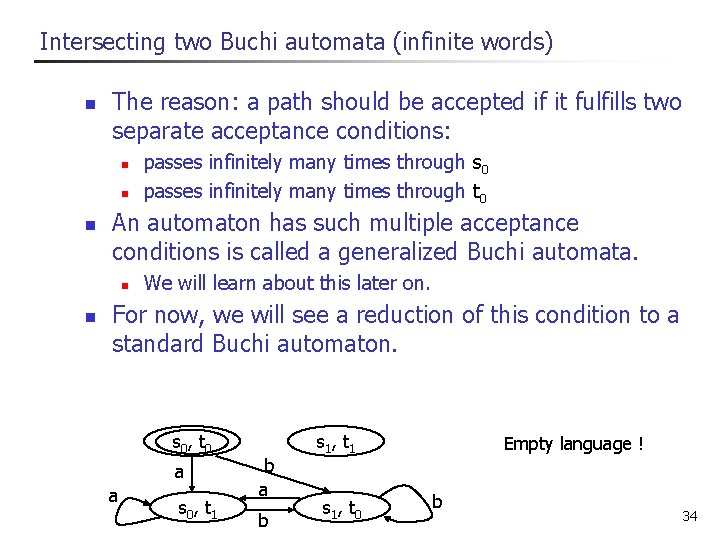
Intersecting two Buchi automata (infinite words) n The reason: a path should be accepted if it fulfills two separate acceptance conditions: n n n An automaton has such multiple acceptance conditions is called a generalized Buchi automata. n n passes infinitely many times through s 0 passes infinitely many times through t 0 We will learn about this later on. For now, we will see a reduction of this condition to a standard Buchi automaton. s 0 , t 0 a a s 0 , t 1 b a b s 1 , t 1 s 1 , t 0 Empty language ! b 34

Intersecting two Buchi automata (infinite words) n Strategy: n n n “Multiply” the product automaton by 3 (S = S 1 £ S 2 £ {0, 1, 2} ) Start from the ‘ 0’ copy. Transition to the ‘ 1’ copy when entering a state from F 1 Transition to the ‘ 2’ copy if in a ‘ 1’ state and entering a state from F 2, and in the next state back to a ‘ 0’ state. Make the ‘ 2’ copy an accepting set. 35

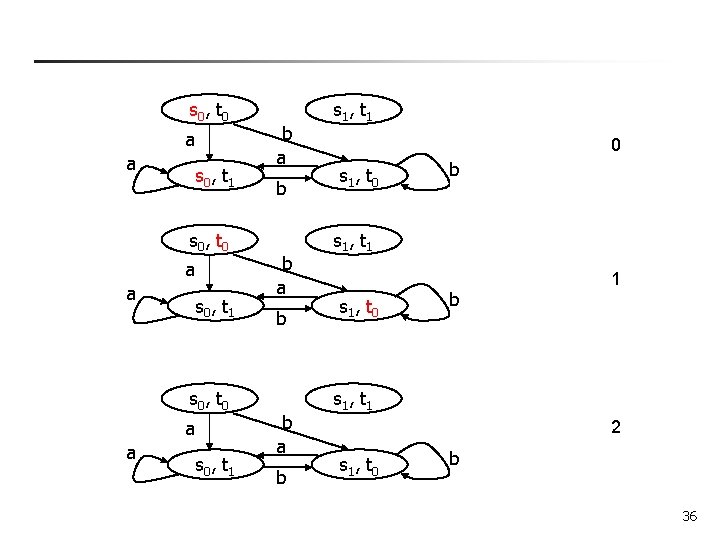
s 0 , t 0 a a s 0 , t 1 b a b s 1 , t 1 0 s 1 , t 0 b s 1 , t 1 s 1 , t 0 b 1 s 1 , t 1 2 s 1 , t 0 b 36

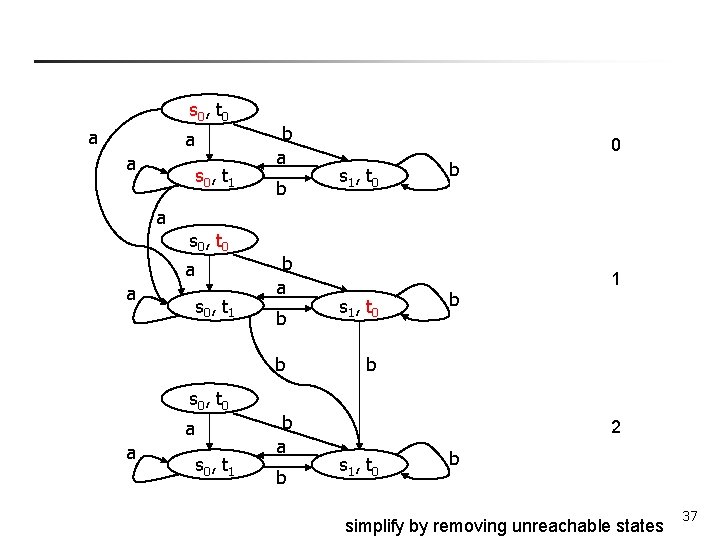
s 0 , t 0 a a a s 0 , t 1 b a b 0 s 1 , t 0 b a s 0 , t 0 a a s 0 , t 1 b a b b s 0 , t 0 a a s 0 , t 1 b a b s 1 , t 0 b 1 b 2 s 1 , t 0 b simplify by removing unreachable states 37

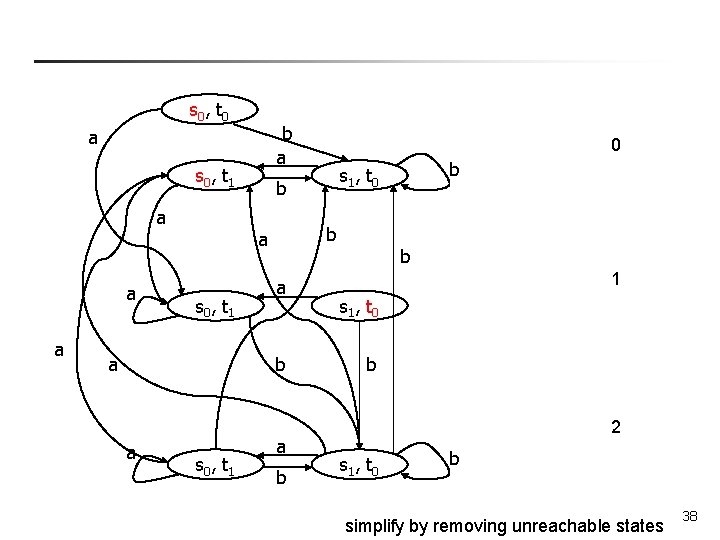
s 0 , t 0 b a a s 0 , t 1 a b a s 0 , t 1 b s 1 , t 0 b a a 0 a b 1 s 1 , t 0 b 2 s 1 , t 0 b simplify by removing unreachable states 38

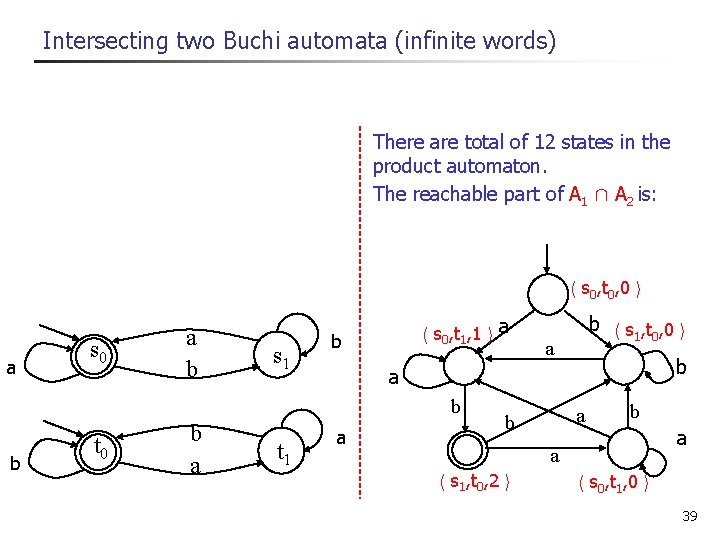
Intersecting two Buchi automata (infinite words) There are total of 12 states in the product automaton. The reachable part of A 1 Å A 2 is: h s 0, t 0, 0 i a s 0 a b s 1 h s 0, t 1, 1 i a b b b a t 1 a b t 0 b h s 1, t 0, 0 i a a b b a h s 1, t 0, 2 i a h s 0, t 1, 0 i 39