Lecture 6 Nondeterministic Finite Automata NFA NFA tape







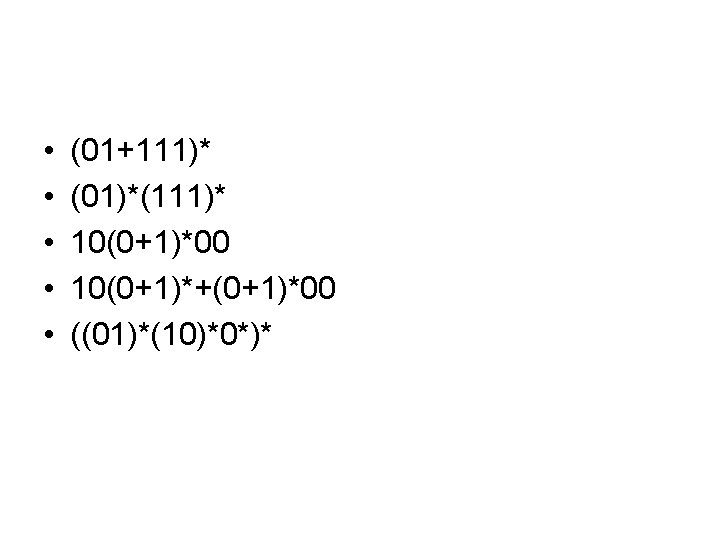
- Slides: 23

Lecture 6 Nondeterministic Finite Automata (NFA)

NFA tape head Finite Control

a l p h a b e t The tape is divided into finitely many cells. Each cell contains a symbol in an alphabet Σ.

a • The head scans at a cell on the tape and can read a symbol on the cell. In each move, the head move to the right cell or stop there (in a ε-move).

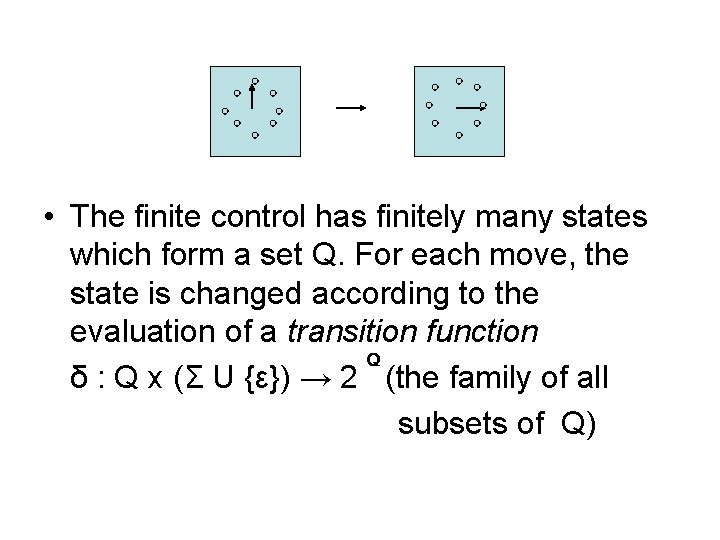
• The finite control has finitely many states which form a set Q. For each move, the state is changed according to the evaluation of a transition function Q δ : Q x (Σ U {ε}) → 2 (the family of all subsets of Q)

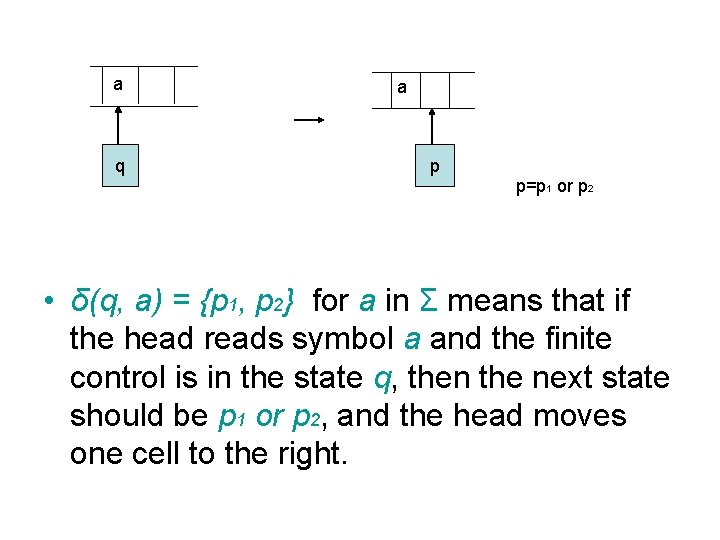
a q a p p=p 1 or p 2 • δ(q, a) = {p 1, p 2} for a in Σ means that if the head reads symbol a and the finite control is in the state q, then the next state should be p 1 or p 2, and the head moves one cell to the right.

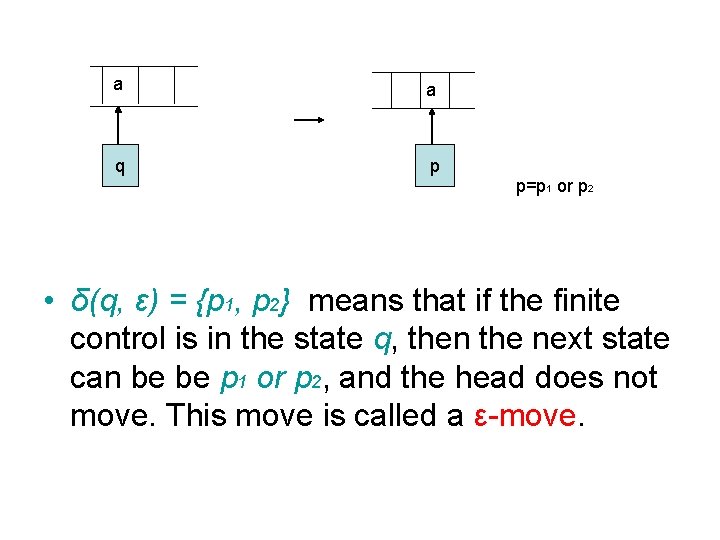
a a q p p=p 1 or p 2 • δ(q, ε) = {p 1, p 2} means that if the finite control is in the state q, then the next state can be be p 1 or p 2, and the head does not move. This move is called a ε-move.

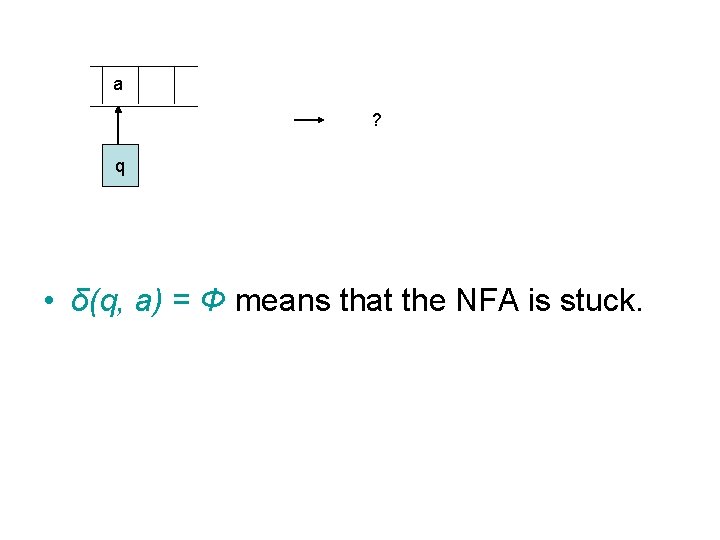
a ? q • δ(q, a) = Φ means that the NFA is stuck.

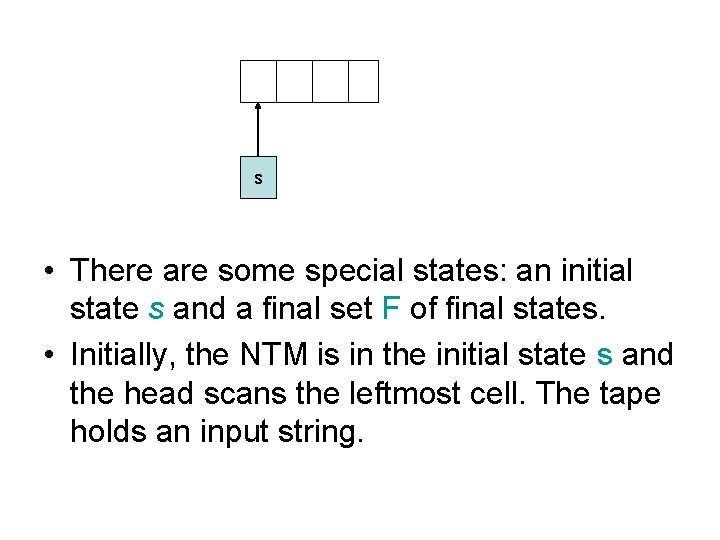
s • There are some special states: an initial state s and a final set F of final states. • Initially, the NTM is in the initial state s and the head scans the leftmost cell. The tape holds an input string.

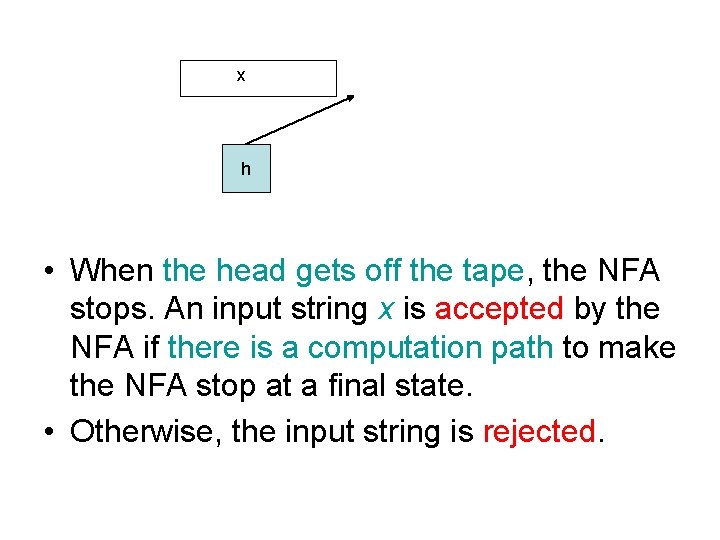
x h • When the head gets off the tape, the NFA stops. An input string x is accepted by the NFA if there is a computation path to make the NFA stop at a final state. • Otherwise, the input string is rejected.

• The NTM can be represented by M = (Q, Σ, δ, s, F) where Σ is the alphabet of input symbols. • The set of all strings accepted by a NFA M is denoted by L(M). We also say that the language L(M) is accepted by M.

• The transition diagram of a NFA is an alternative way to represent the DFA. • For M = (Q, Σ, δ, s, F), the transition diagram of M is a symbol-labeled digraph G=(V, E) satisfying the following: V = Q (s = E={q a , f= for f in F) p | p in δ(q, a)}.

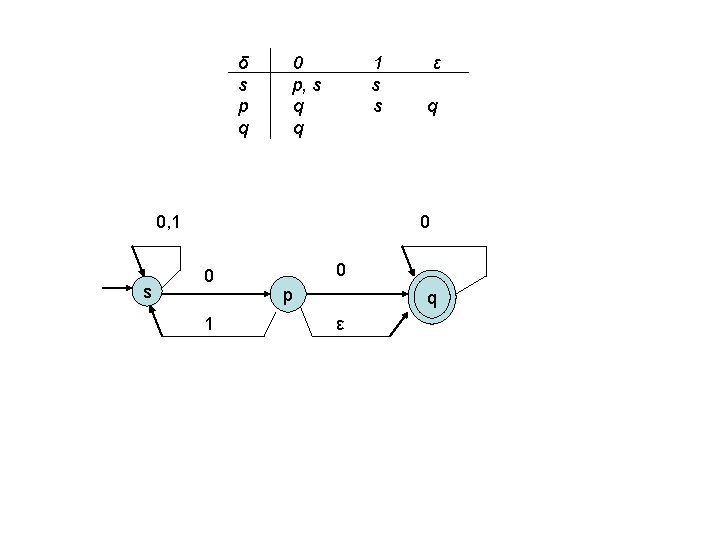
δ s p q 0 p, s q q 1 s s 0, 1 s ε q 0 0 1 0 p q ε

Theorem 1 • Every regular language can be accepted by an NFA.

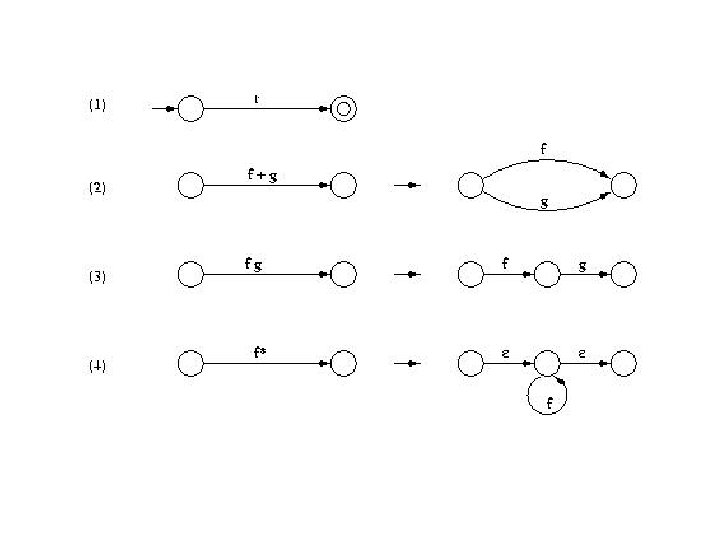
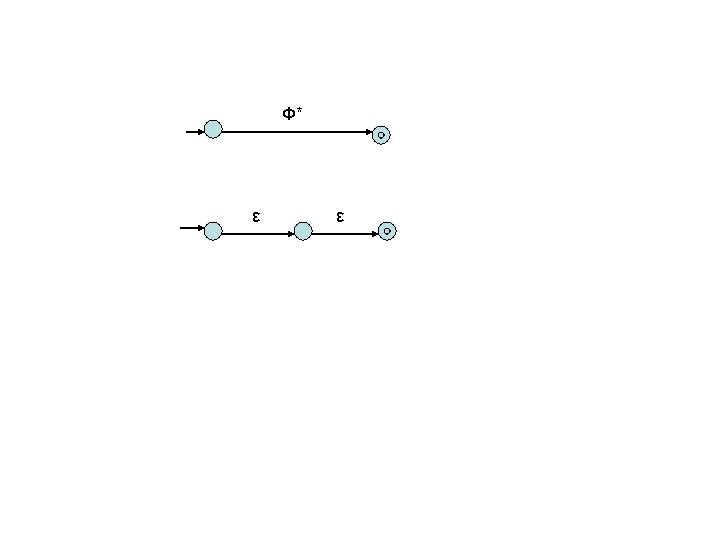
G(r) • For each regular expression r, we can construct a digraph G(r) with edges labeled by symbols and ε as follows. • If r=Φ, then • If r≠Φ, then



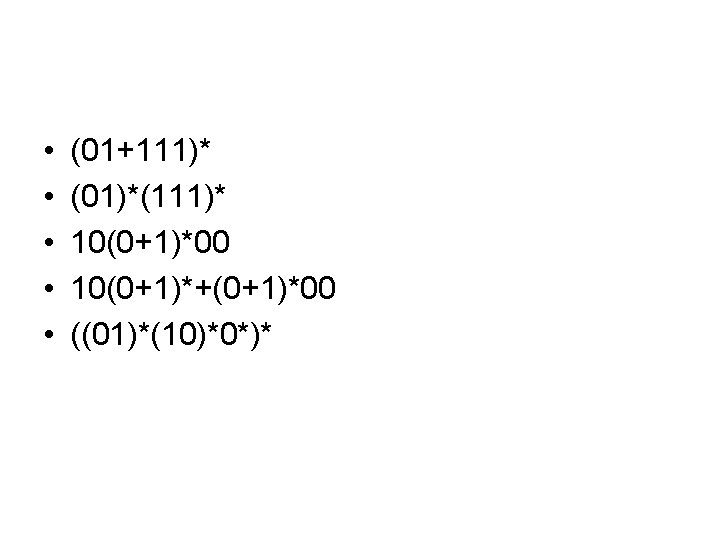
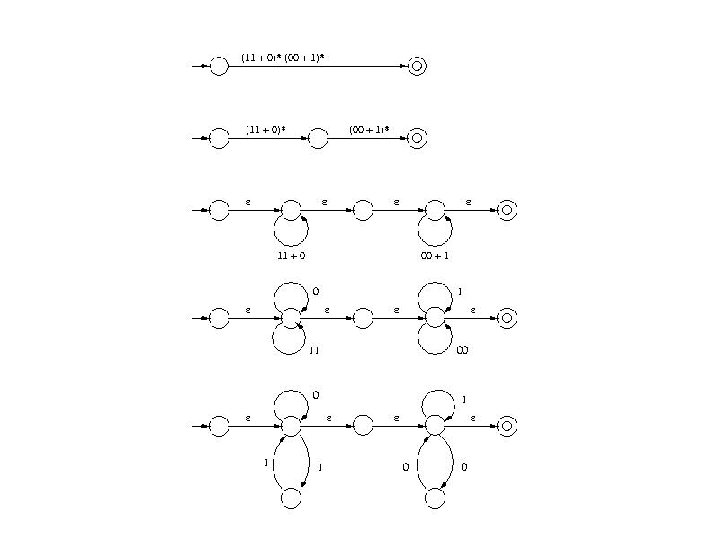
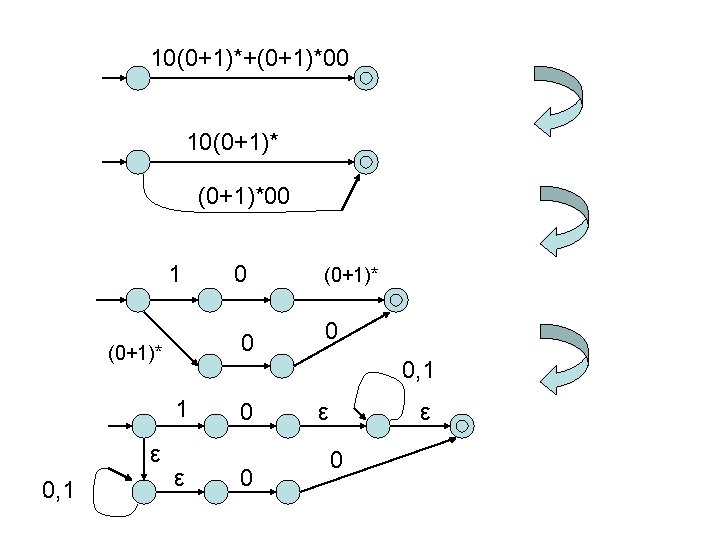
• • • (01+111)* (01)*(111)* 10(0+1)*00 10(0+1)*+(0+1)*00 ((01)*(10)*0*)*

10(0+1)*+(0+1)*00 10(0+1)*00 1 0 (0+1)* 0, 1 (0+1)* 0 0, 1 1 ε 0 0 ε ε 0

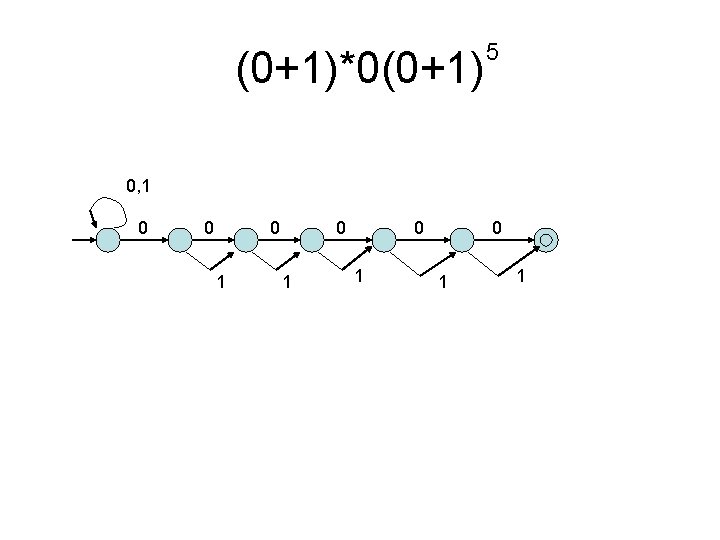
(0+1)*0(0+1) 5 0, 1 0 0 0 1 0 1 1

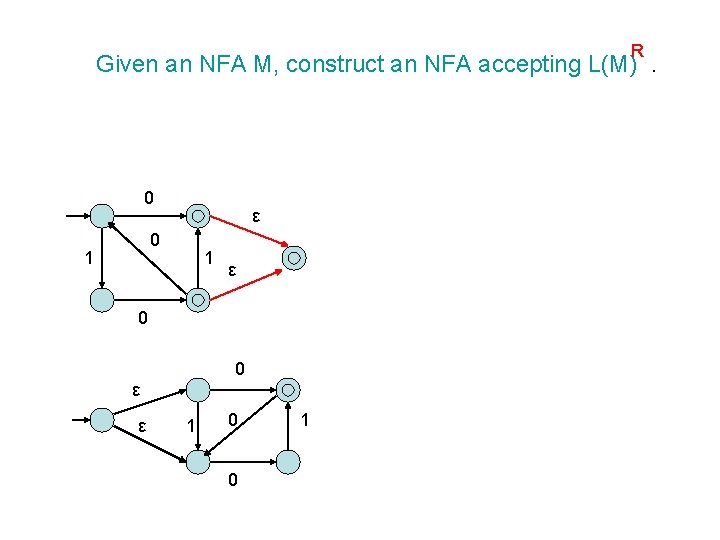
R Given an NFA M, construct an NFA accepting L(M). 0 ε 0 1 1 ε 0 0 ε ε 1 0 0 1

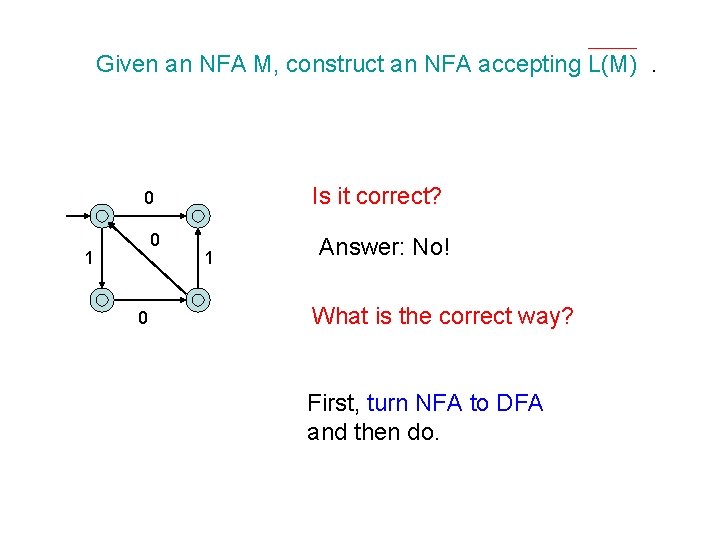
Given an NFA M, construct an NFA accepting L(M). Is it correct? 0 0 1 Answer: No! What is the correct way? First, turn NFA to DFA and then do.