NonDeterministic Finite Automata Prof Busch LSU 1 Nondeterministic

Non-Deterministic Finite Automata Prof. Busch - LSU 1

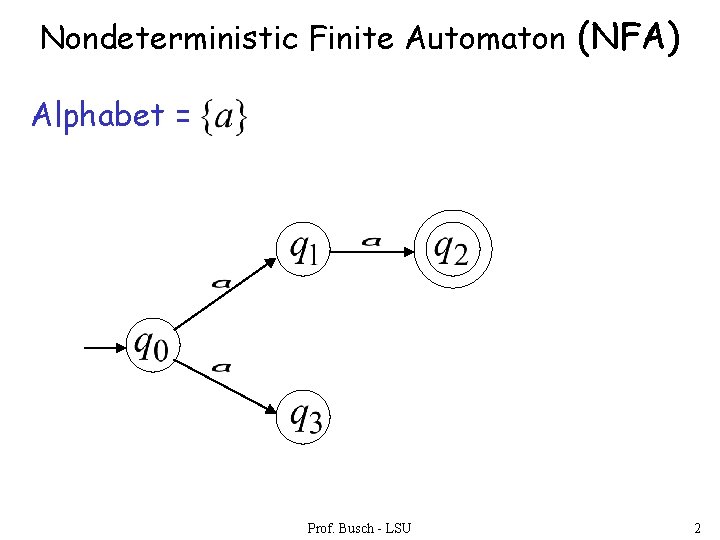
Nondeterministic Finite Automaton (NFA) Alphabet = Prof. Busch - LSU 2

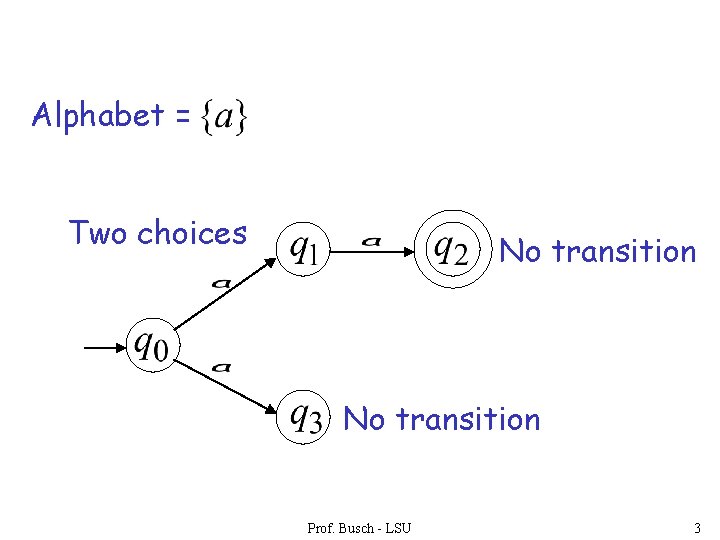
Alphabet = Two choices No transition Prof. Busch - LSU 3

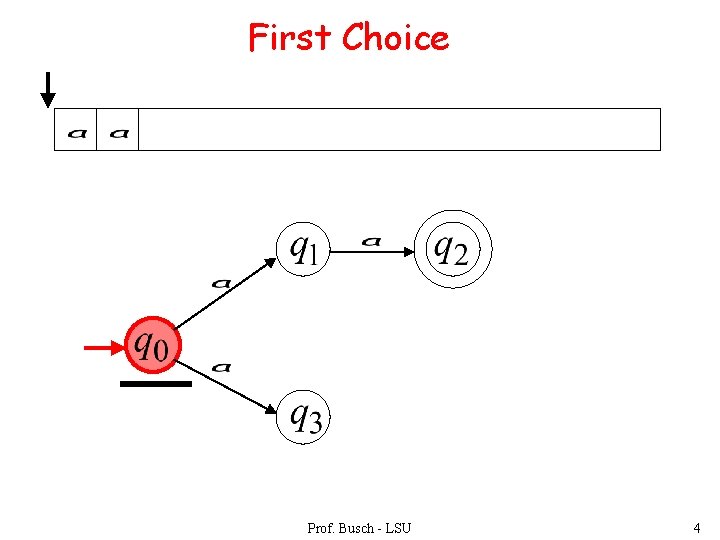
First Choice Prof. Busch - LSU 4

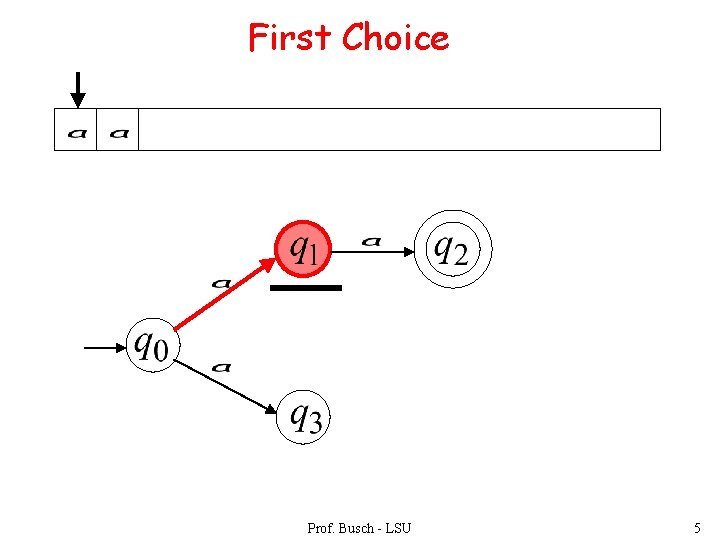
First Choice Prof. Busch - LSU 5

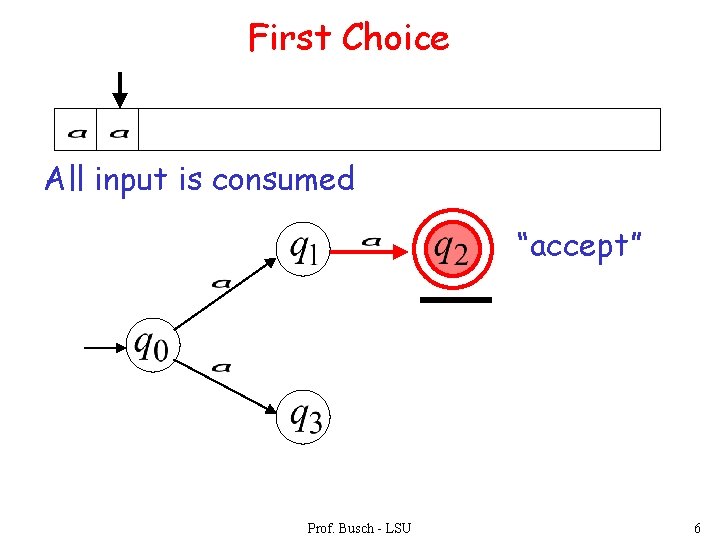
First Choice All input is consumed “accept” Prof. Busch - LSU 6

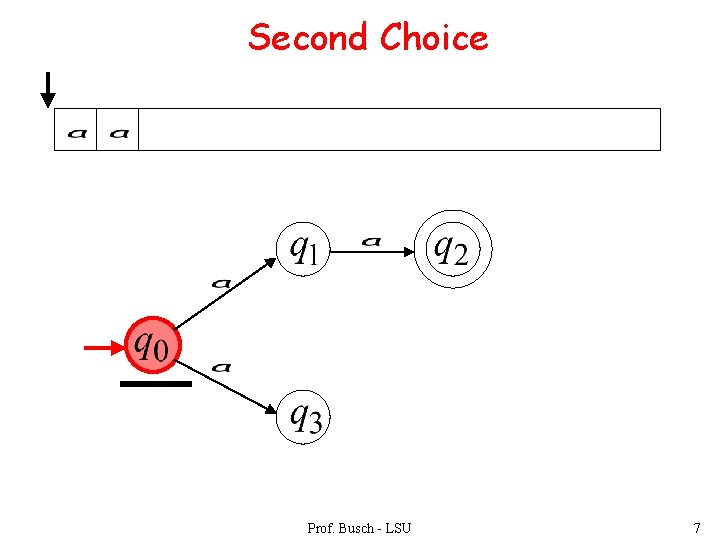
Second Choice Prof. Busch - LSU 7

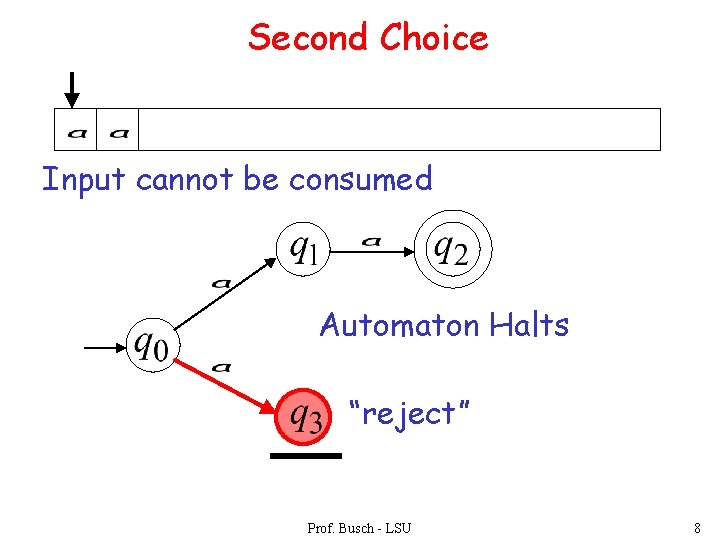
Second Choice Input cannot be consumed Automaton Halts “reject” Prof. Busch - LSU 8

An NFA accepts a string: if there is a computation of the NFA that accepts the string i. e. , all the input string is processed and the automaton is in an accepting state Prof. Busch - LSU 9

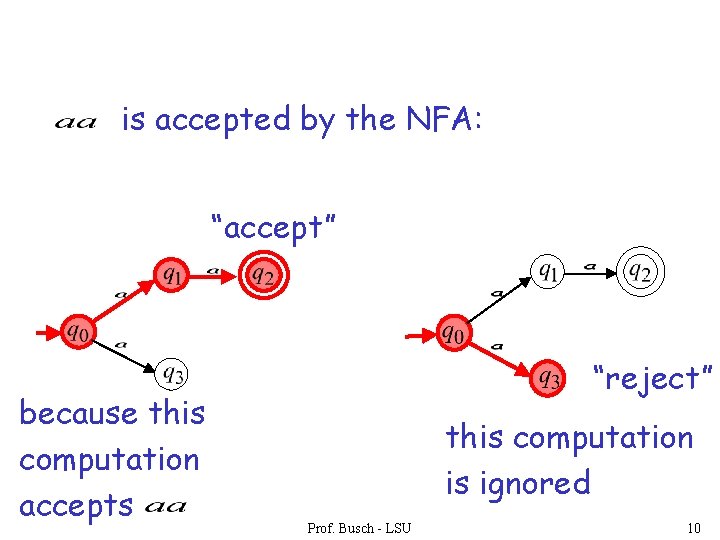
is accepted by the NFA: “accept” because this computation accepts “reject” this computation is ignored Prof. Busch - LSU 10

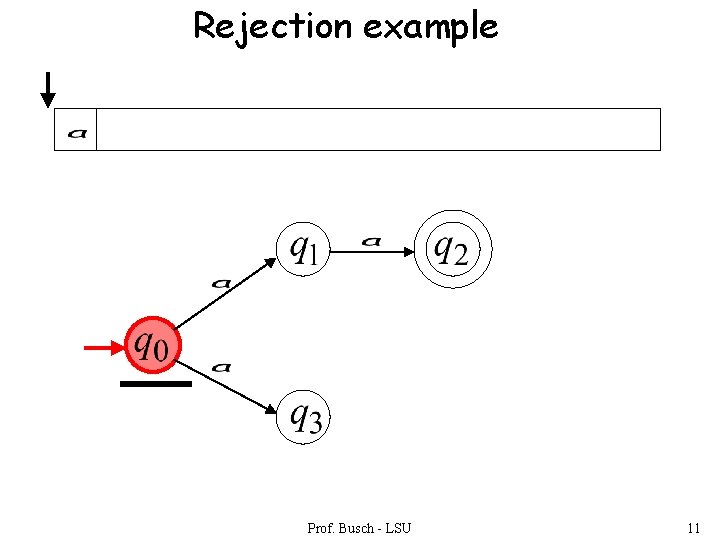
Rejection example Prof. Busch - LSU 11

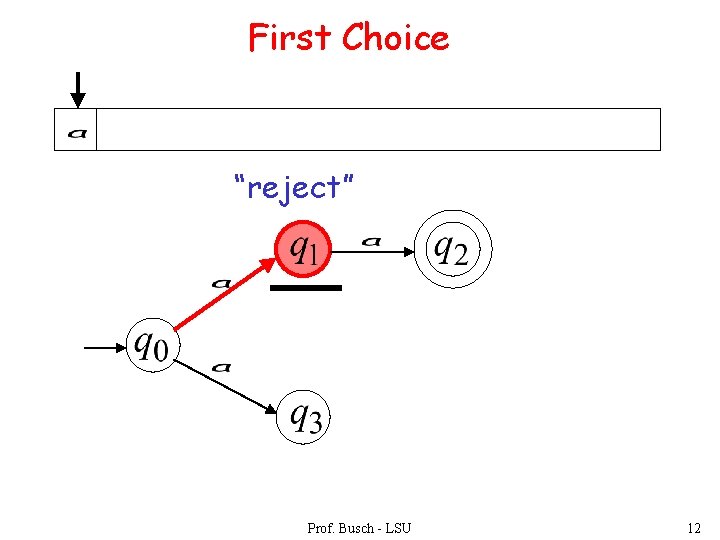
First Choice “reject” Prof. Busch - LSU 12

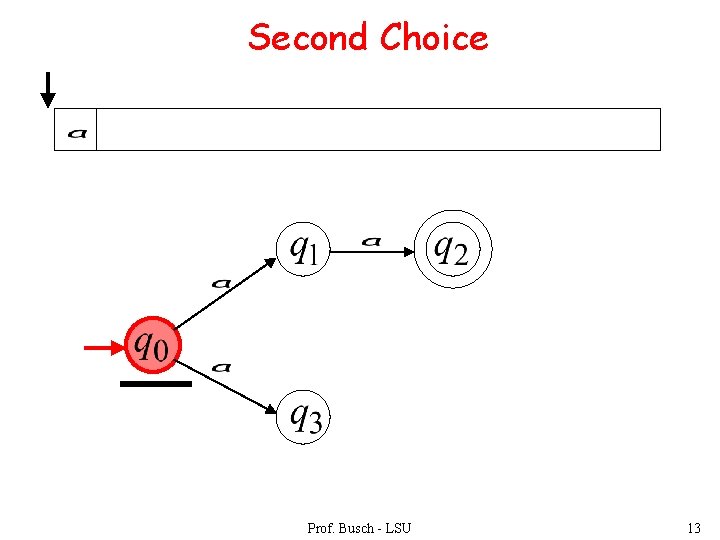
Second Choice Prof. Busch - LSU 13

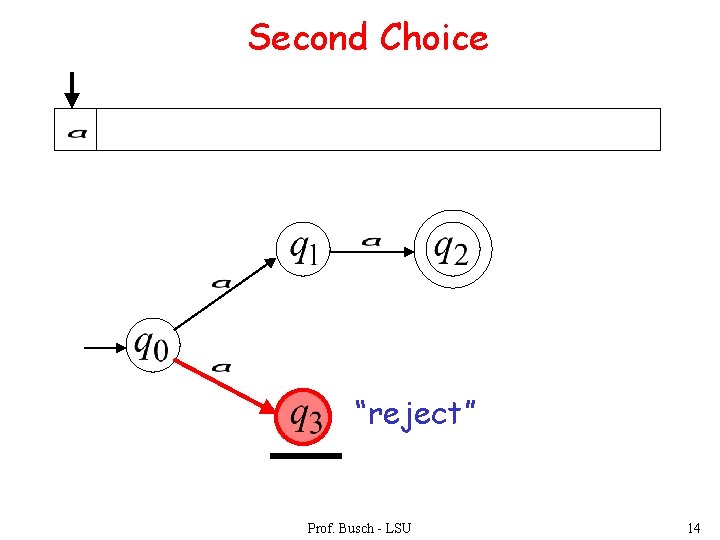
Second Choice “reject” Prof. Busch - LSU 14

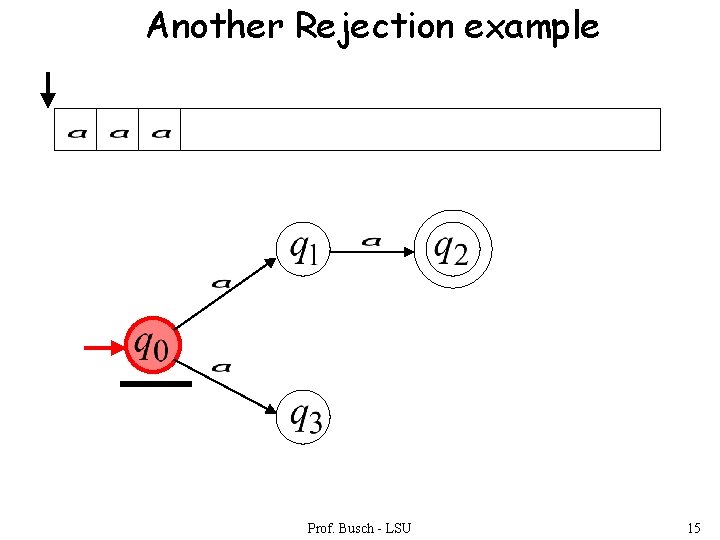
Another Rejection example Prof. Busch - LSU 15

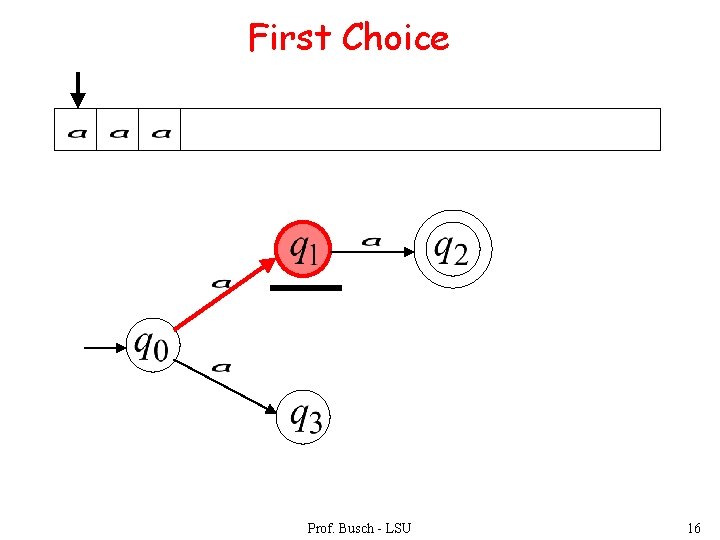
First Choice Prof. Busch - LSU 16

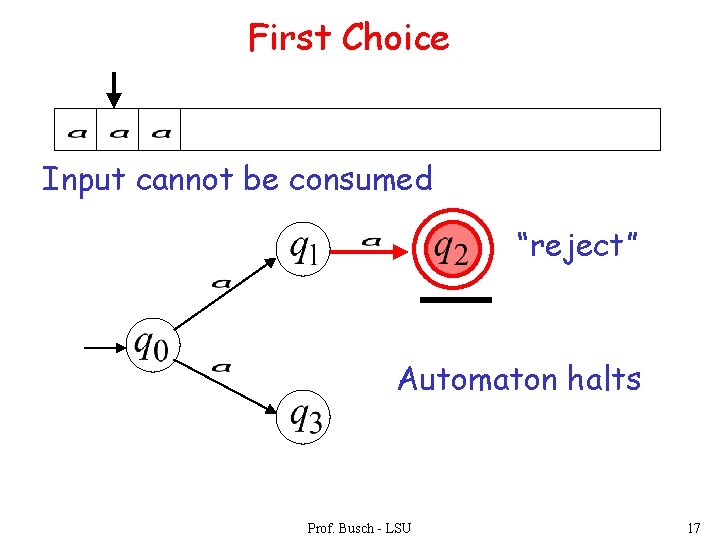
First Choice Input cannot be consumed “reject” Automaton halts Prof. Busch - LSU 17

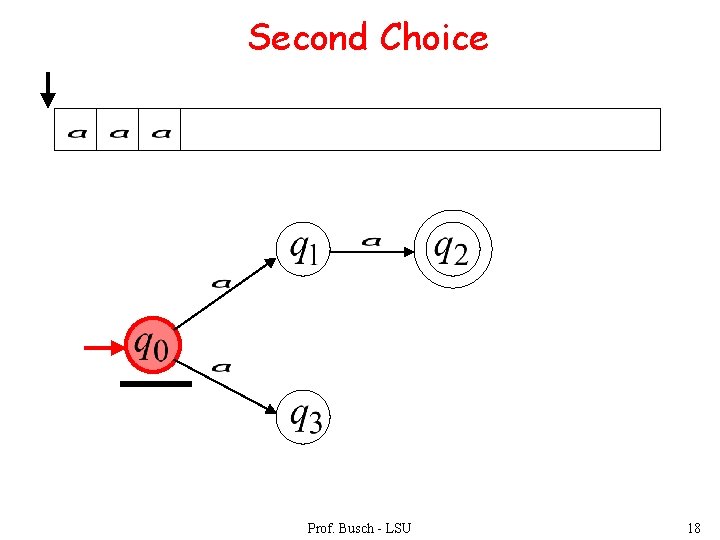
Second Choice Prof. Busch - LSU 18

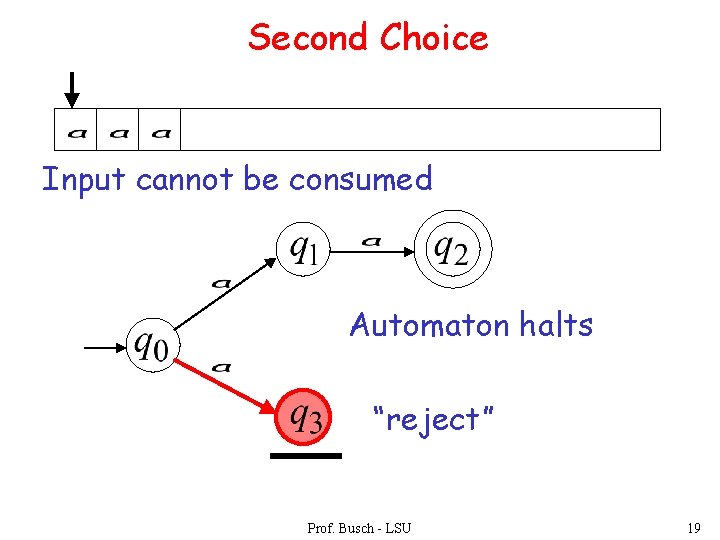
Second Choice Input cannot be consumed Automaton halts “reject” Prof. Busch - LSU 19

An NFA rejects a string: if there is no computation of the NFA that accepts the string. For each computation: • All the input is consumed and the automaton is in a non accepting state OR • The input cannot be consumed Prof. Busch - LSU 20

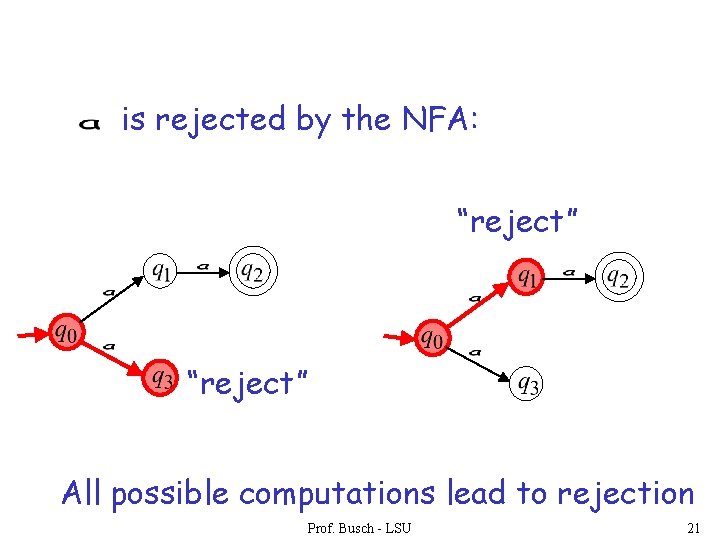
is rejected by the NFA: “reject” All possible computations lead to rejection Prof. Busch - LSU 21

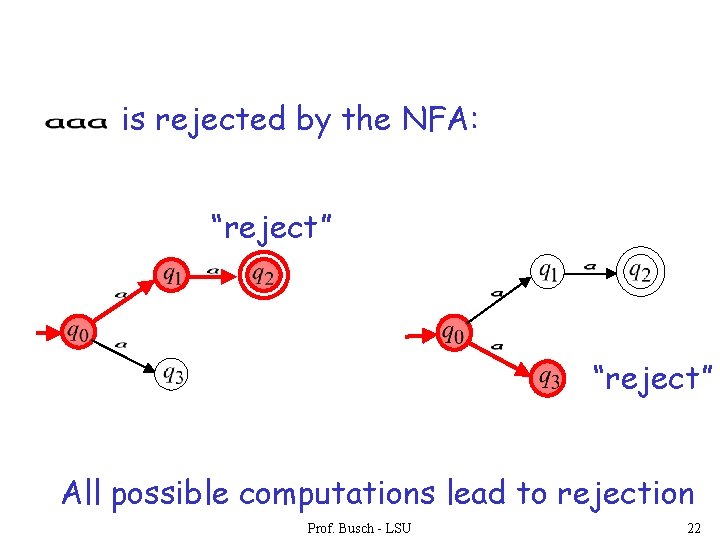
is rejected by the NFA: “reject” All possible computations lead to rejection Prof. Busch - LSU 22

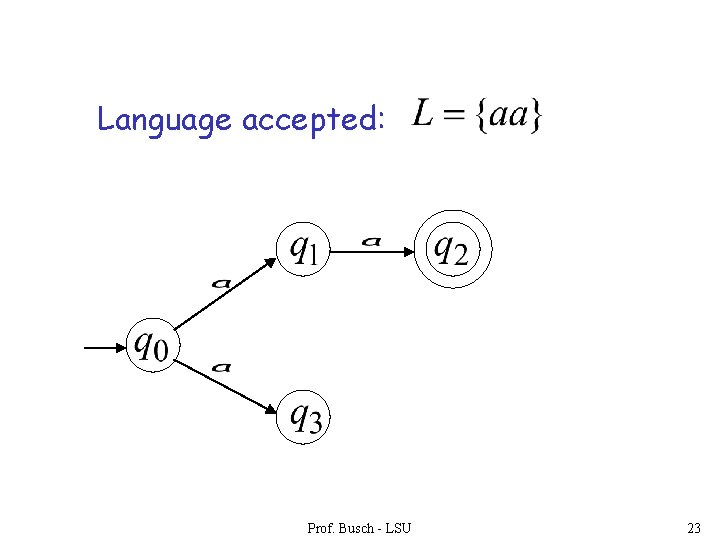
Language accepted: Prof. Busch - LSU 23

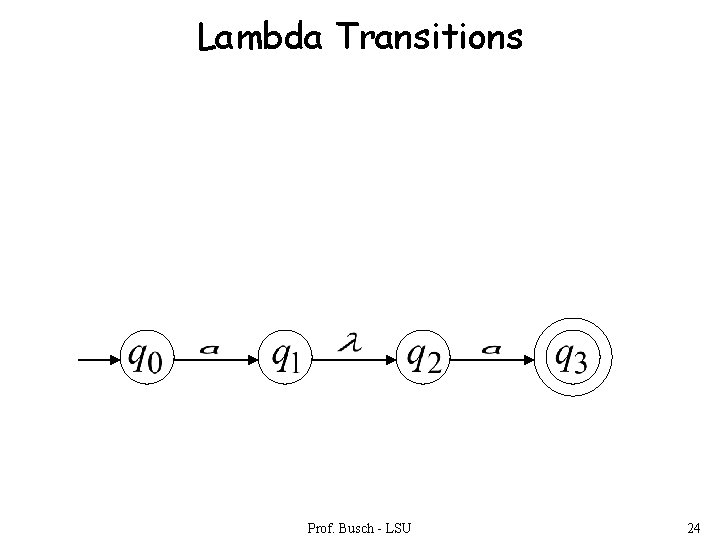
Lambda Transitions Prof. Busch - LSU 24

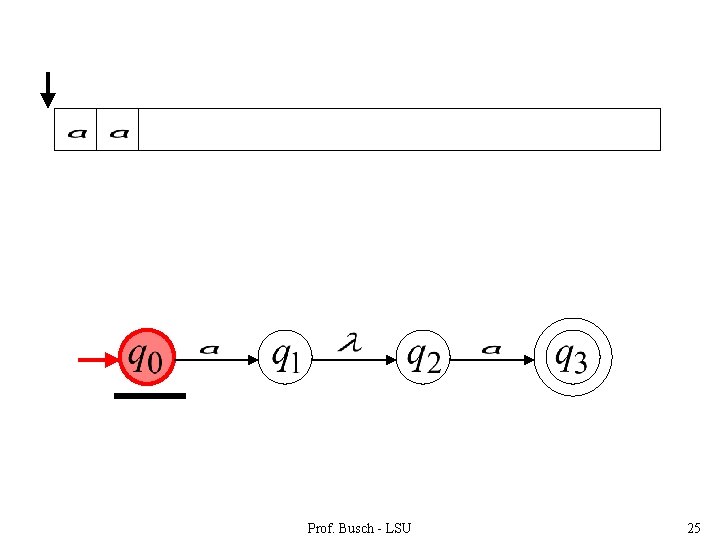
Prof. Busch - LSU 25

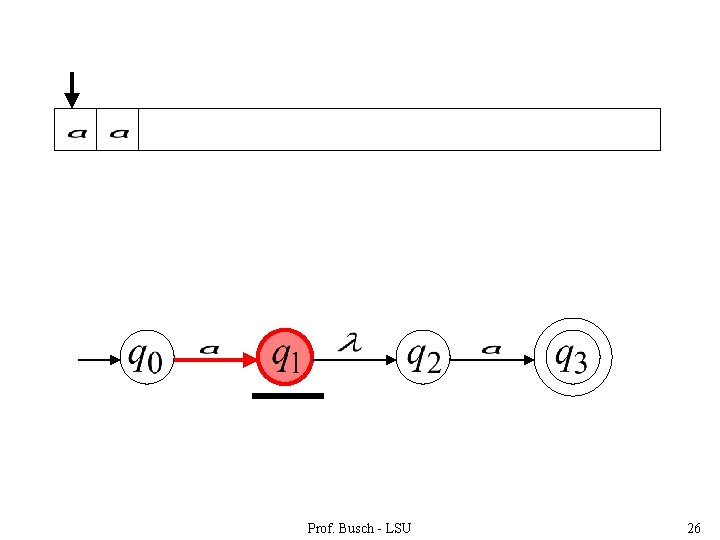
Prof. Busch - LSU 26

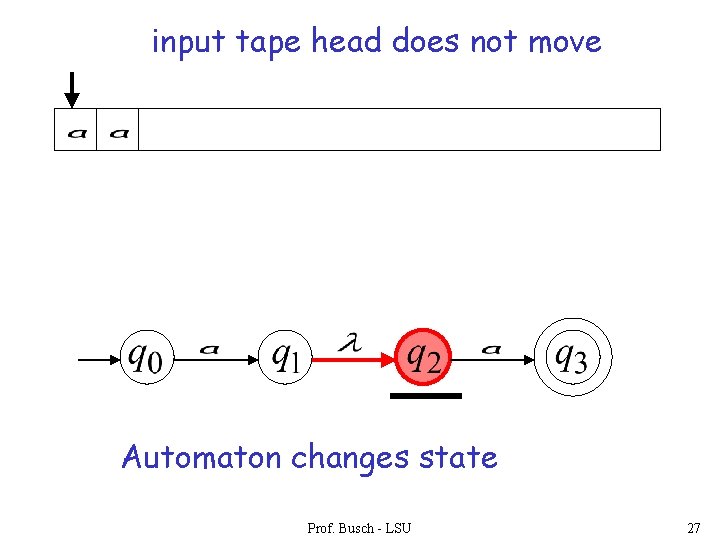
input tape head does not move Automaton changes state Prof. Busch - LSU 27

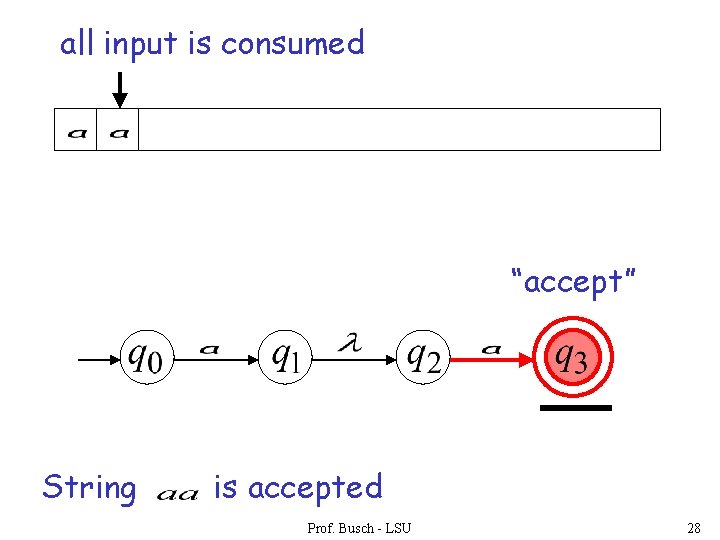
all input is consumed “accept” String is accepted Prof. Busch - LSU 28

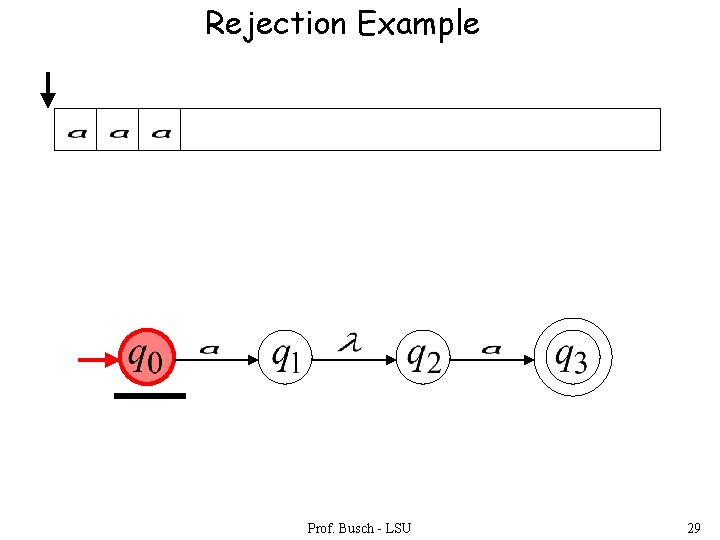
Rejection Example Prof. Busch - LSU 29

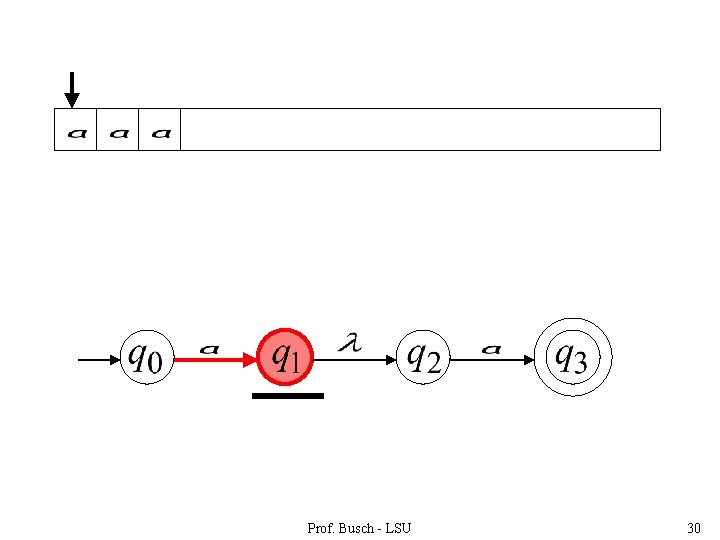
Prof. Busch - LSU 30

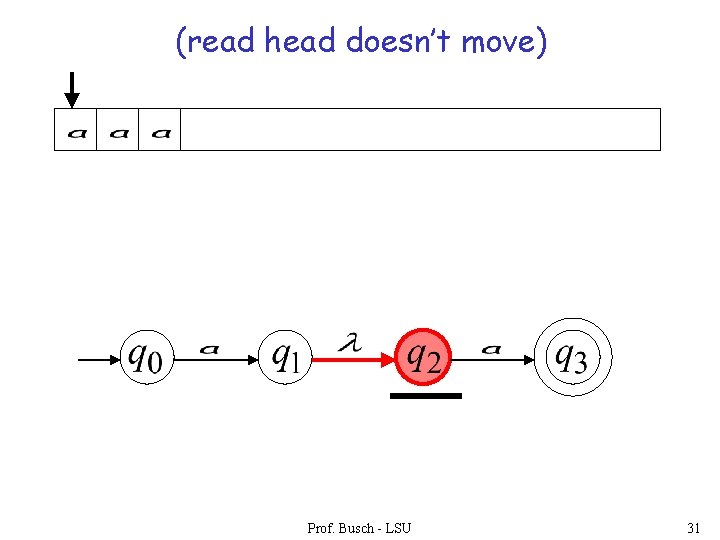
(read head doesn’t move) Prof. Busch - LSU 31

Input cannot be consumed Automaton halts “reject” String is rejected Prof. Busch - LSU 32

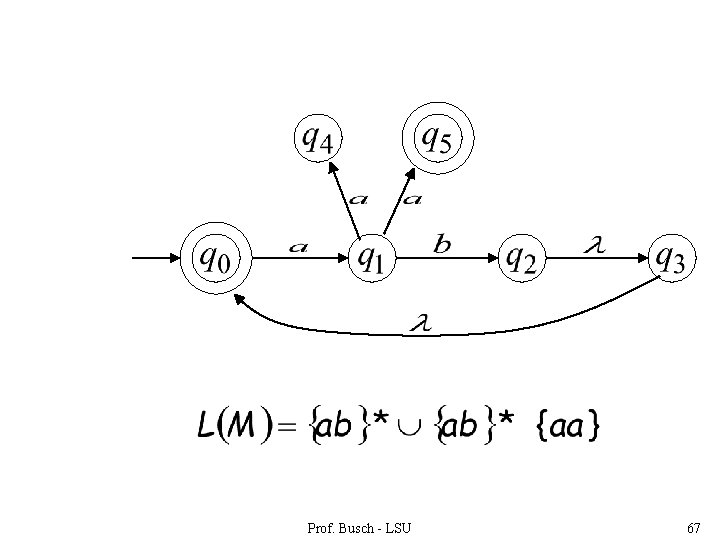
Language accepted: Prof. Busch - LSU 33

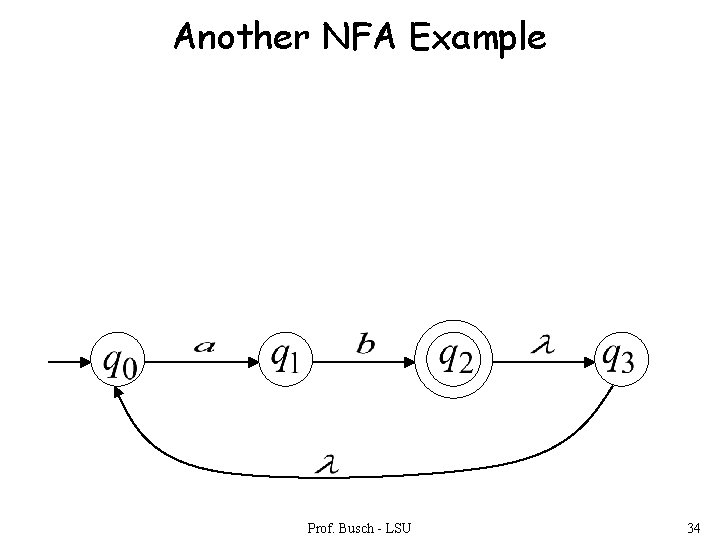
Another NFA Example Prof. Busch - LSU 34

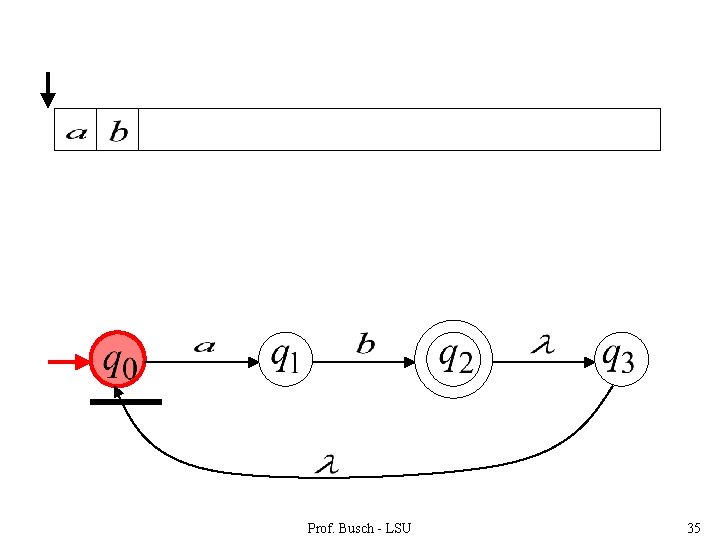
Prof. Busch - LSU 35

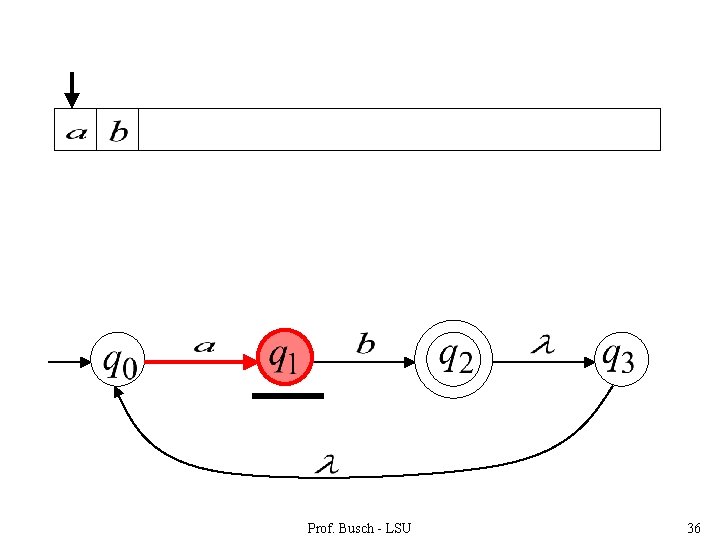
Prof. Busch - LSU 36

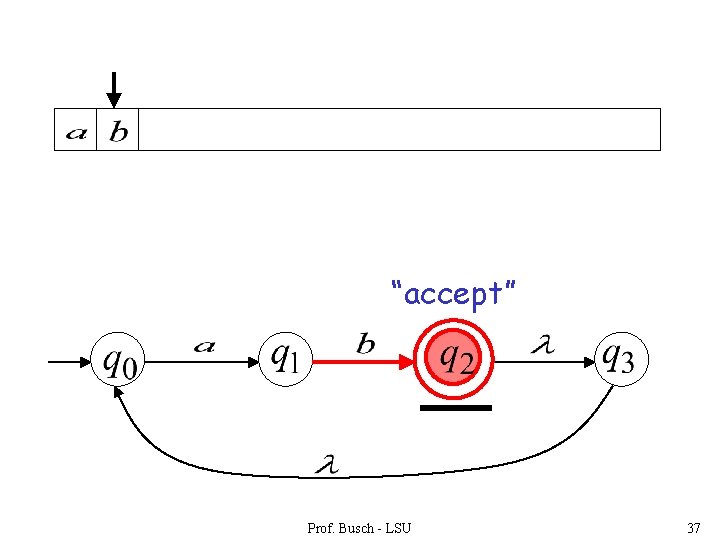
“accept” Prof. Busch - LSU 37

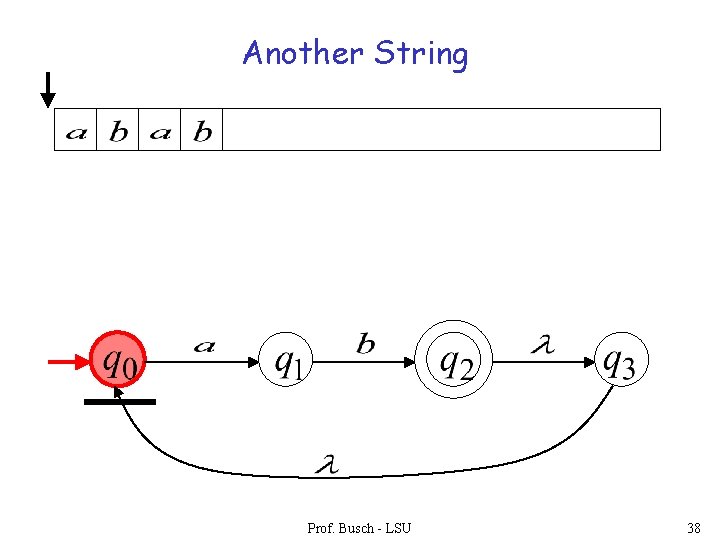
Another String Prof. Busch - LSU 38

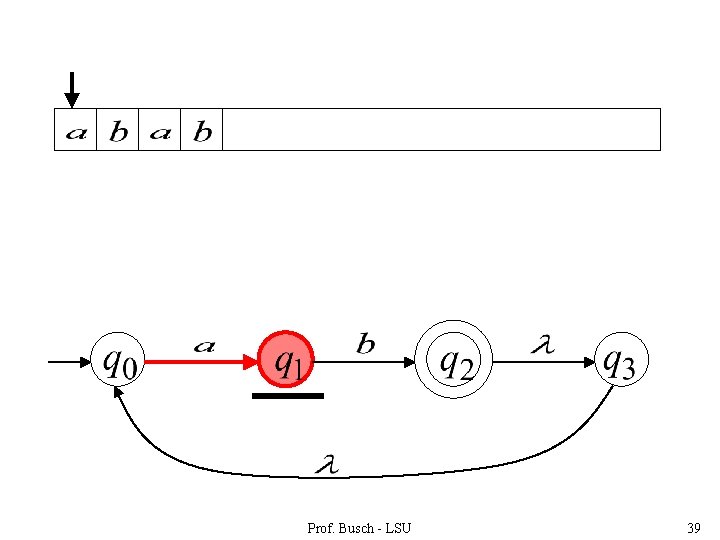
Prof. Busch - LSU 39

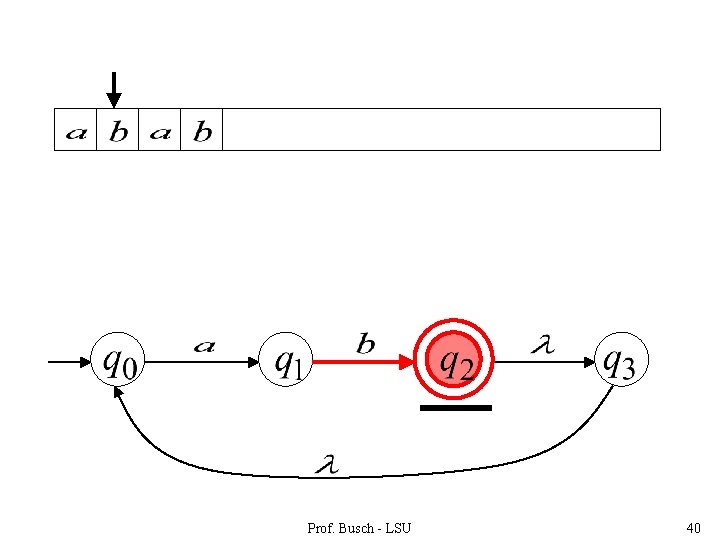
Prof. Busch - LSU 40

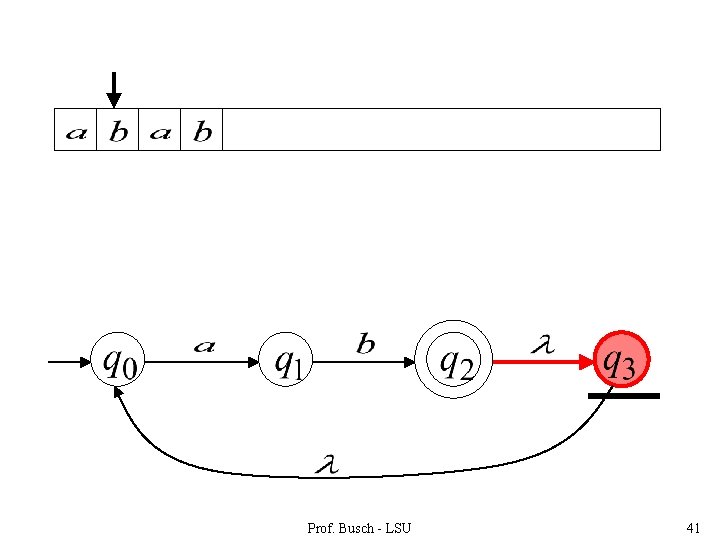
Prof. Busch - LSU 41

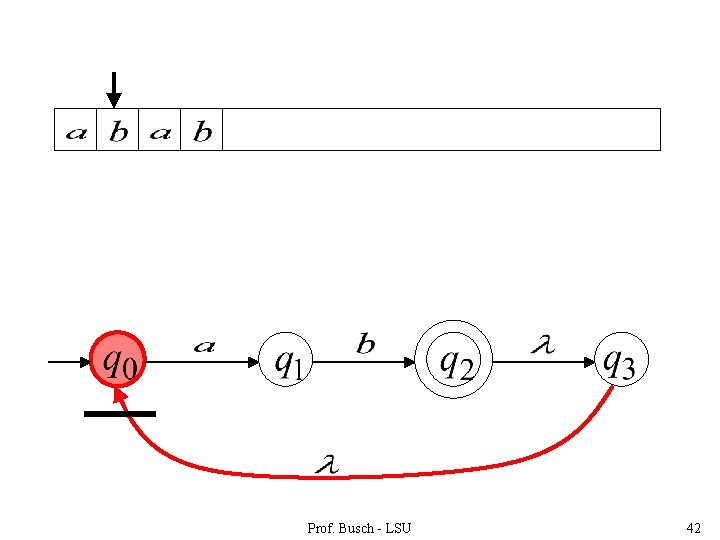
Prof. Busch - LSU 42

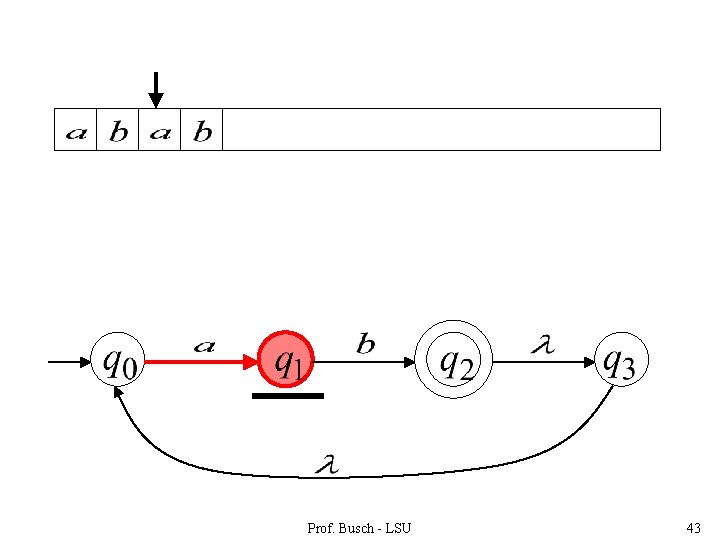
Prof. Busch - LSU 43

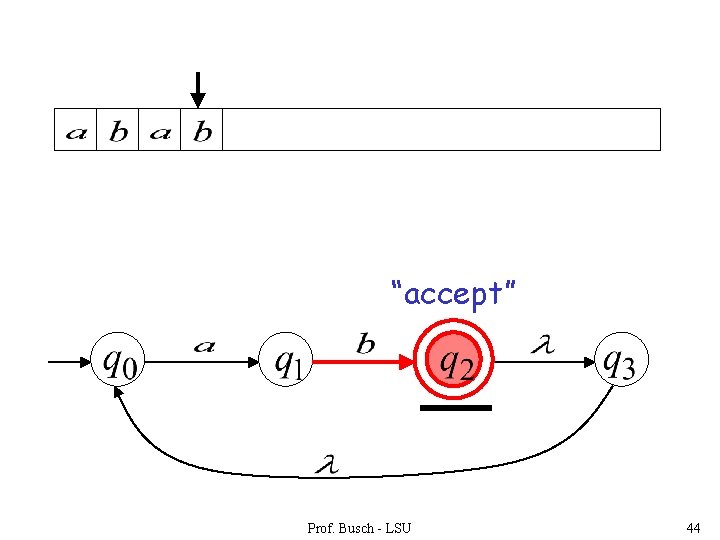
“accept” Prof. Busch - LSU 44

Language accepted Prof. Busch - LSU 45

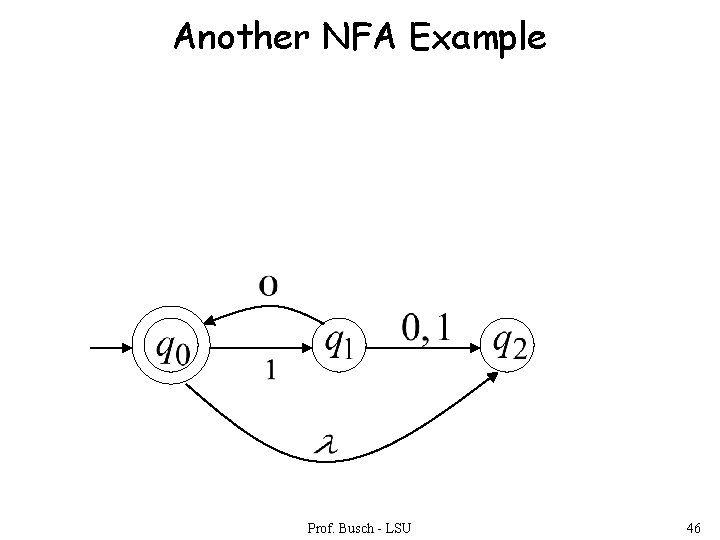
Another NFA Example Prof. Busch - LSU 46

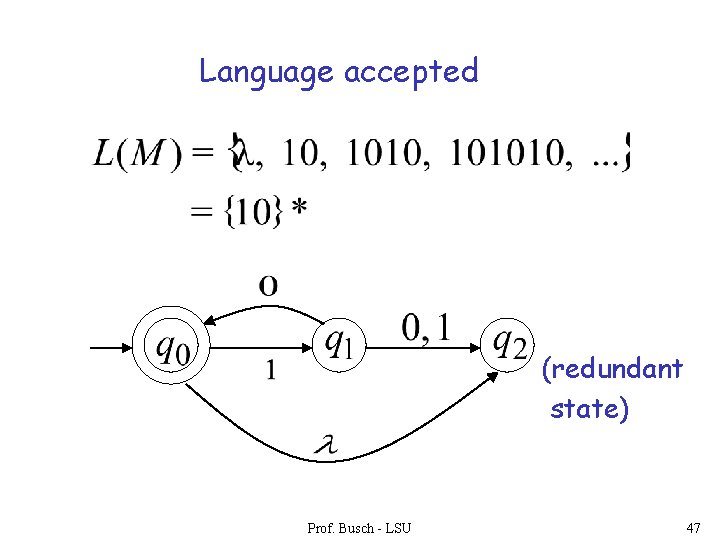
Language accepted (redundant state) Prof. Busch - LSU 47

Remarks: • The symbol never appears on the input tape • Simple automata: Prof. Busch - LSU 48

• NFAs are interesting because we can express languages easier than DFAs NFA DFA Prof. Busch - LSU 49

Formal Definition of NFAs Set of states, i. e. Input aplhabet, i. e. Transition function Initial state Accepting states Prof. Busch - LSU 50

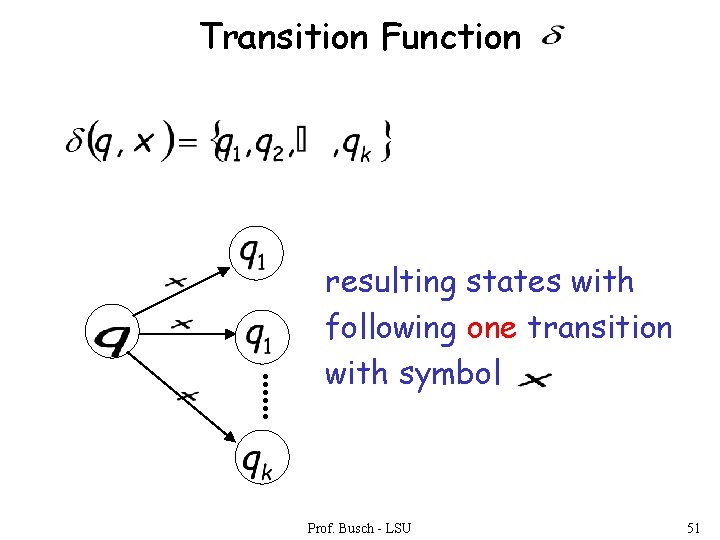
Transition Function resulting states with following one transition with symbol Prof. Busch - LSU 51

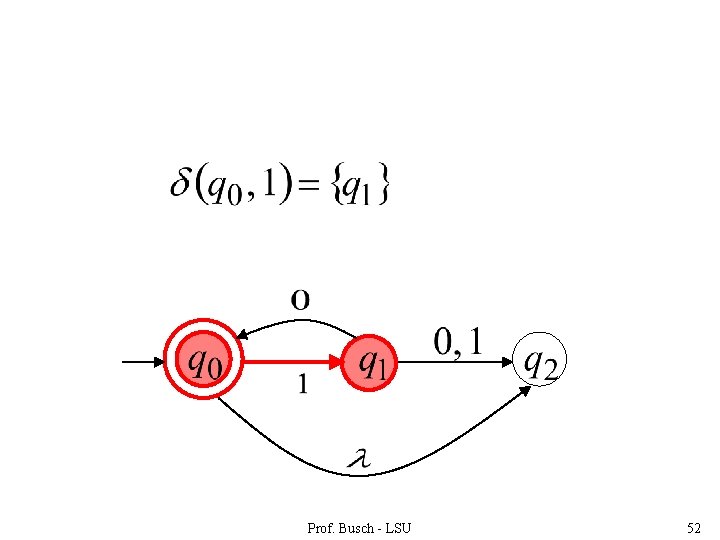
Prof. Busch - LSU 52

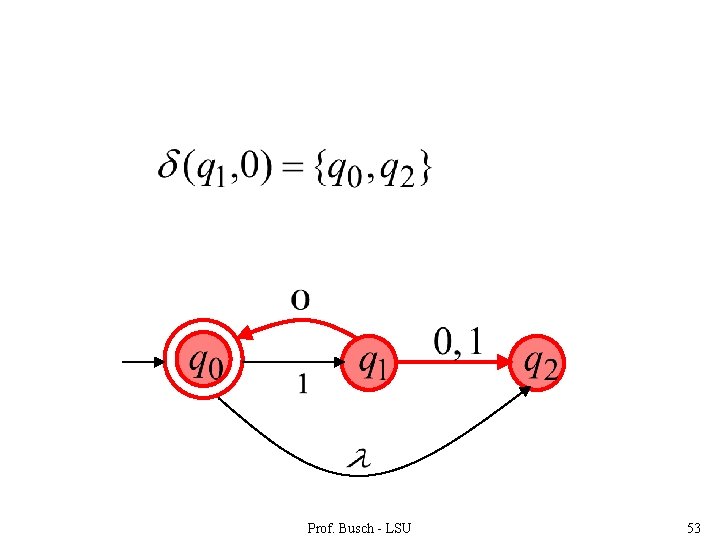
Prof. Busch - LSU 53

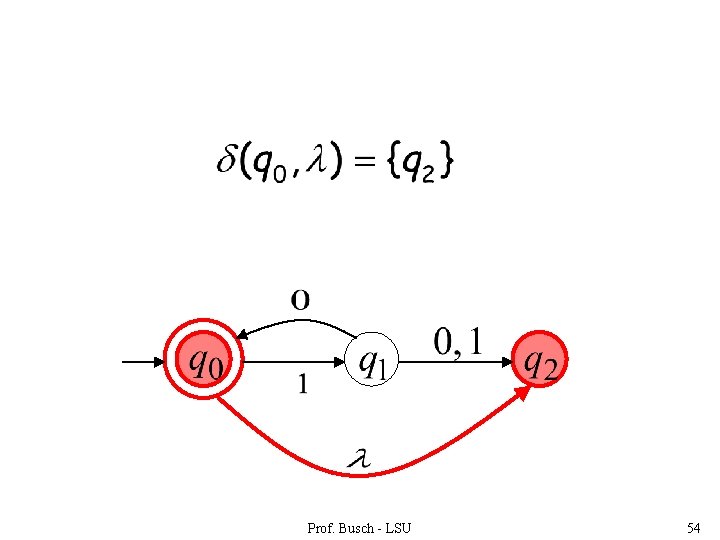
Prof. Busch - LSU 54

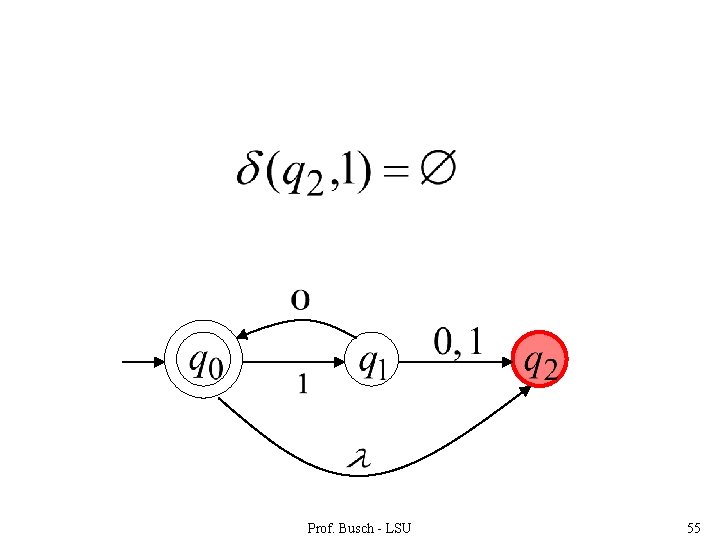
Prof. Busch - LSU 55

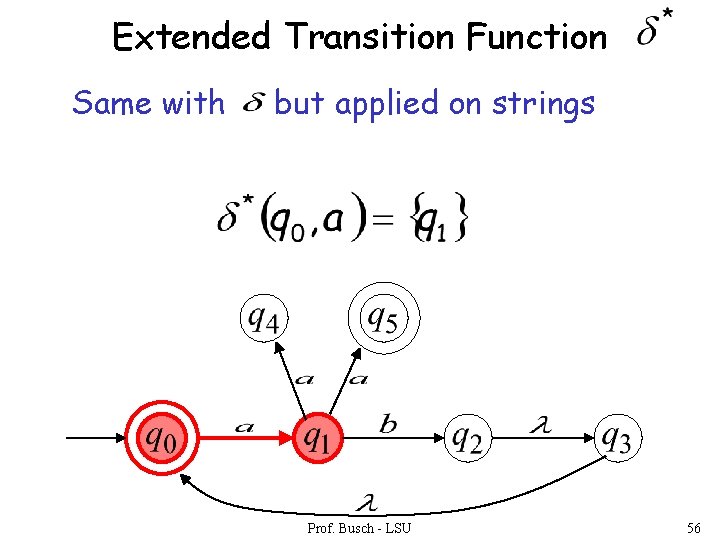
Extended Transition Function Same with but applied on strings Prof. Busch - LSU 56

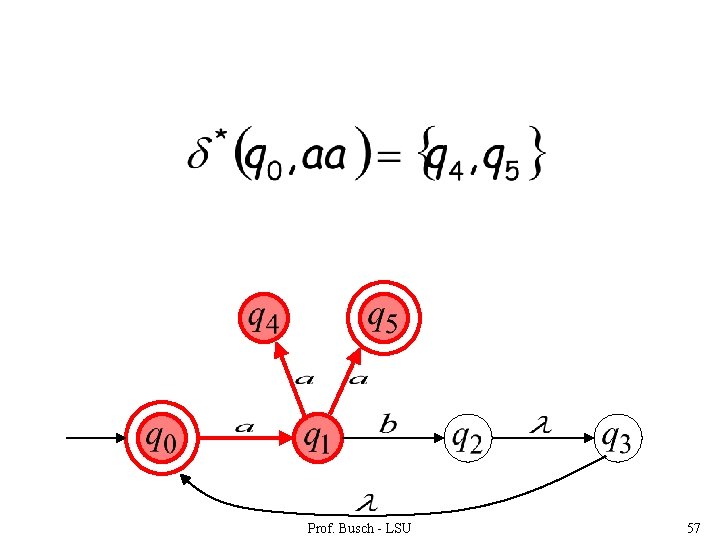
Prof. Busch - LSU 57

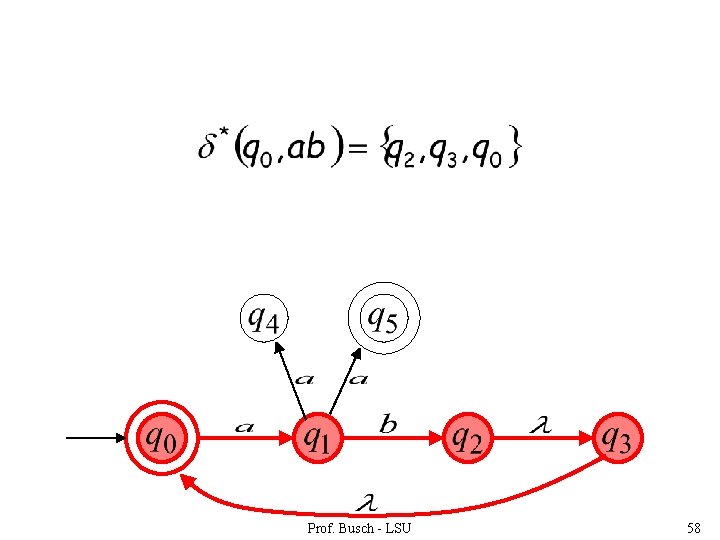
Prof. Busch - LSU 58

Special case: for any state Prof. Busch - LSU 59

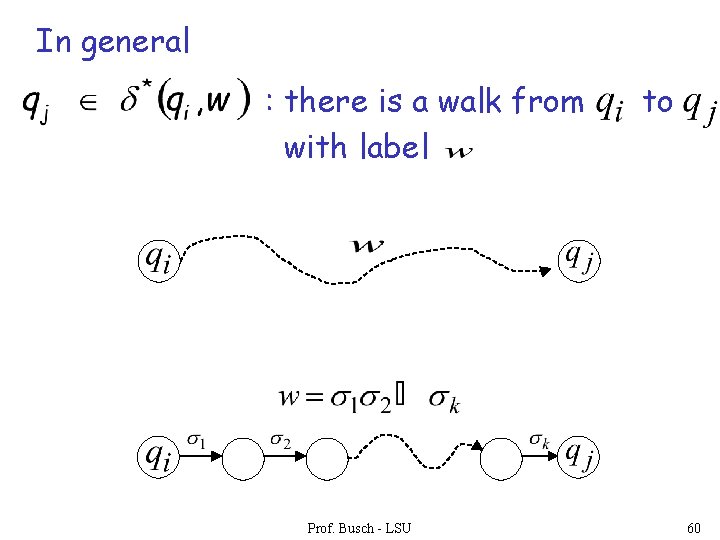
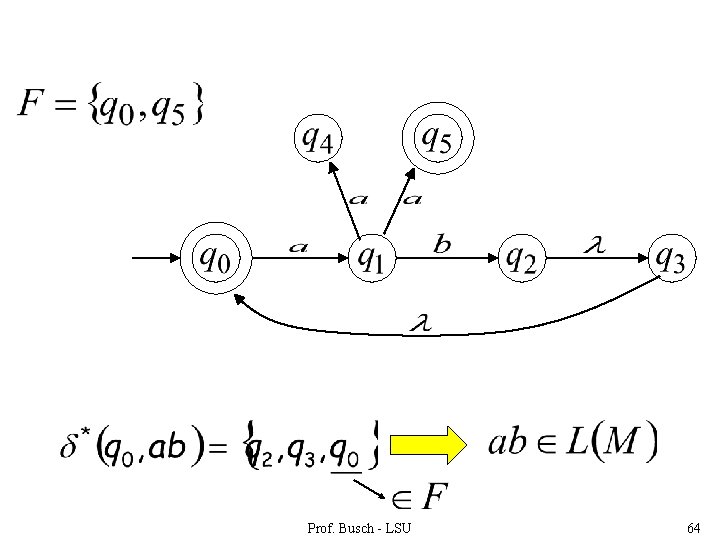
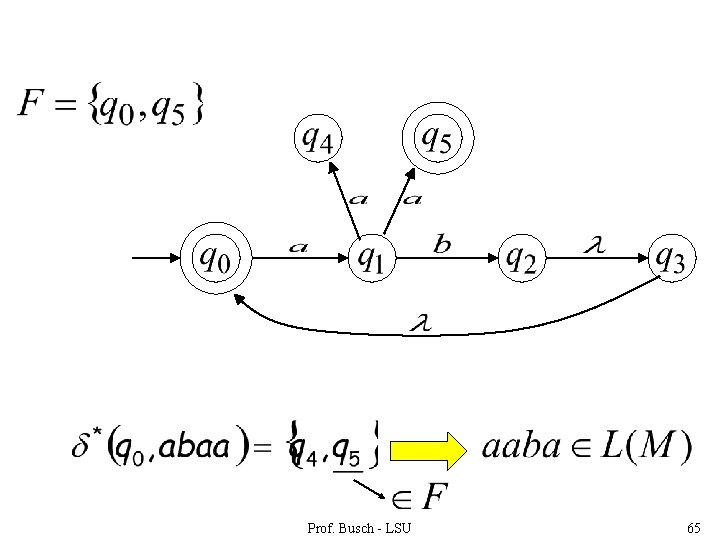
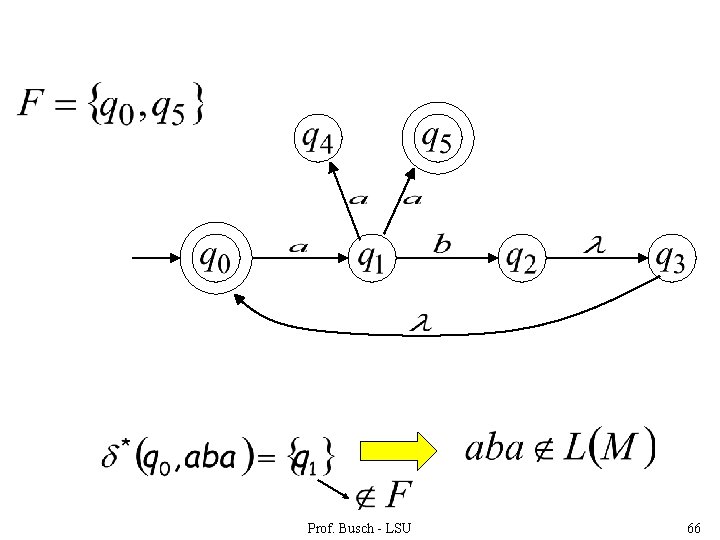
In general : there is a walk from with label Prof. Busch - LSU to 60

The Language of an NFA The language accepted by is: where (accepting state) and there is some Prof. Busch - LSU 61

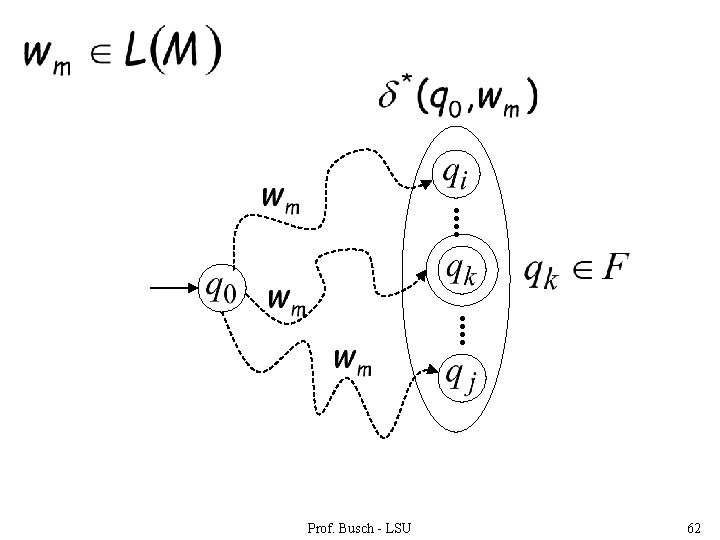
Prof. Busch - LSU 62

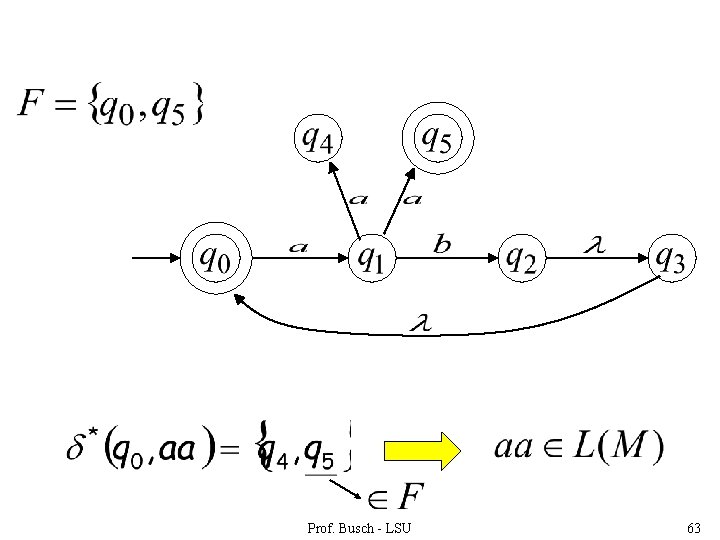
Prof. Busch - LSU 63

Prof. Busch - LSU 64

Prof. Busch - LSU 65

Prof. Busch - LSU 66

Prof. Busch - LSU 67

NFAs accept the Regular Languages Prof. Busch - LSU 68

Equivalence of Machines Definition: Machine is equivalent to machine if Prof. Busch - LSU 69

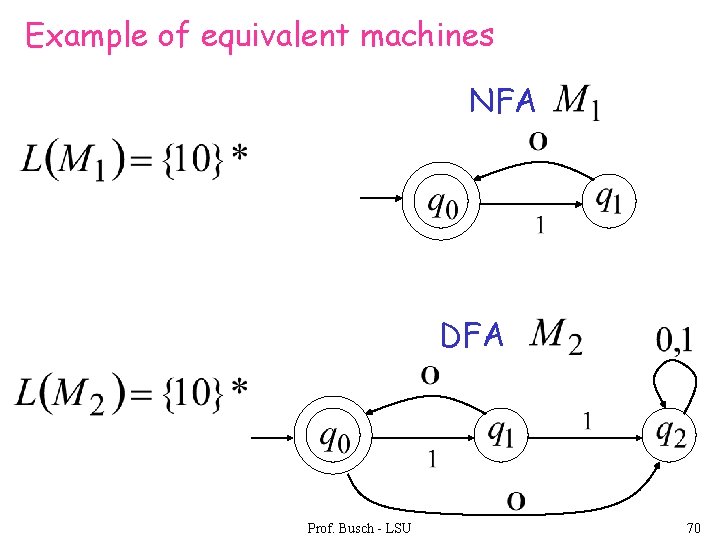
Example of equivalent machines NFA DFA Prof. Busch - LSU 70

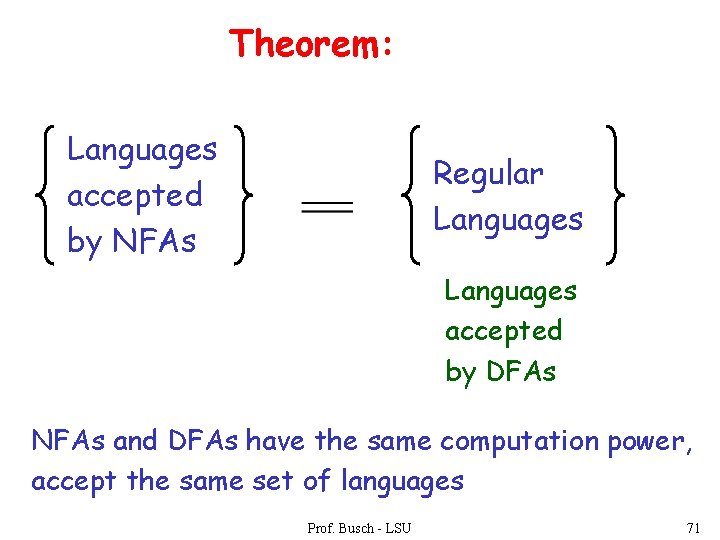
Theorem: Languages accepted by NFAs Regular Languages accepted by DFAs NFAs and DFAs have the same computation power, accept the same set of languages Prof. Busch - LSU 71

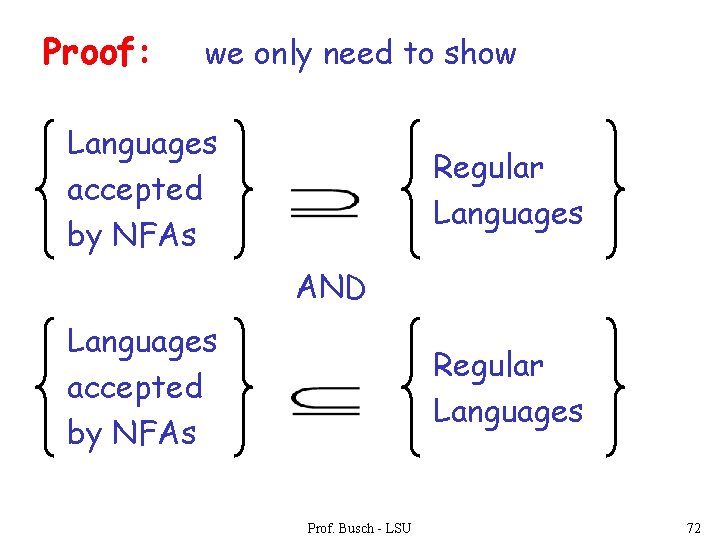
Proof: we only need to show Languages accepted by NFAs Regular Languages AND Languages accepted by NFAs Regular Languages Prof. Busch - LSU 72

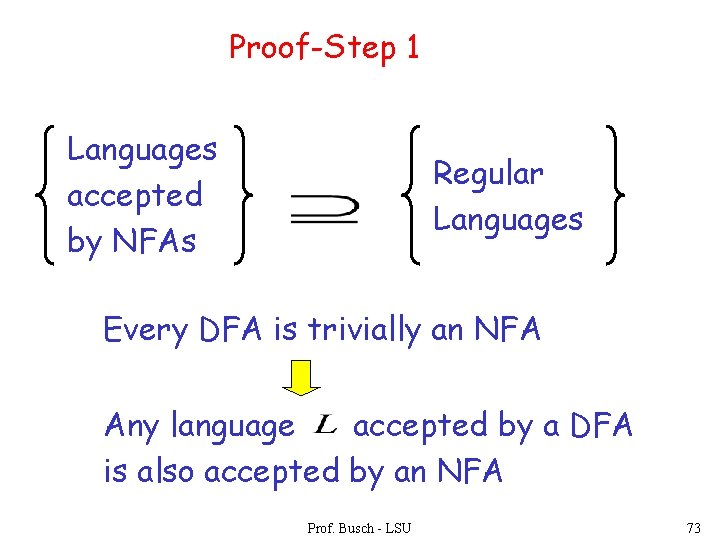
Proof-Step 1 Languages accepted by NFAs Regular Languages Every DFA is trivially an NFA Any language accepted by a DFA is also accepted by an NFA Prof. Busch - LSU 73

Proof-Step 2 Languages accepted by NFAs Regular Languages Any NFA can be converted to an equivalent DFA Any language accepted by an NFA is also accepted by a DFA Prof. Busch - LSU 74

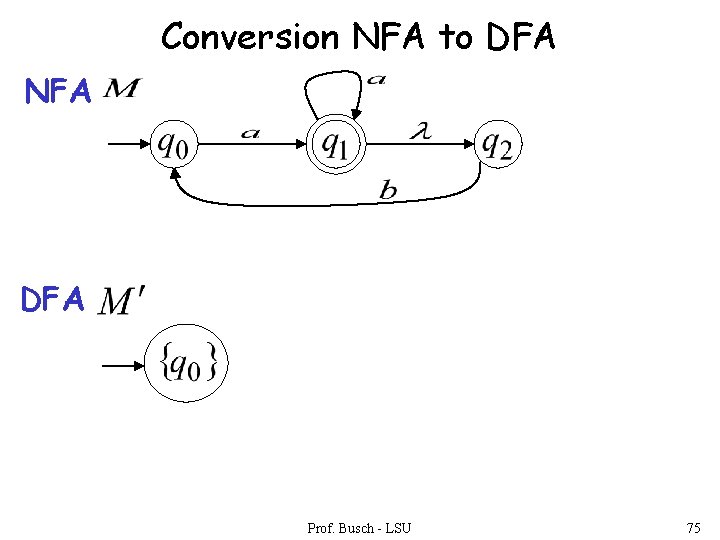
Conversion NFA to DFA NFA DFA Prof. Busch - LSU 75

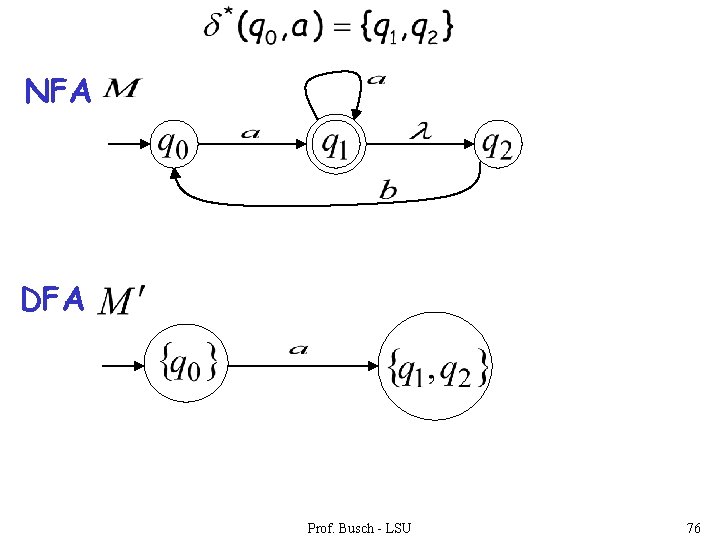
NFA DFA Prof. Busch - LSU 76

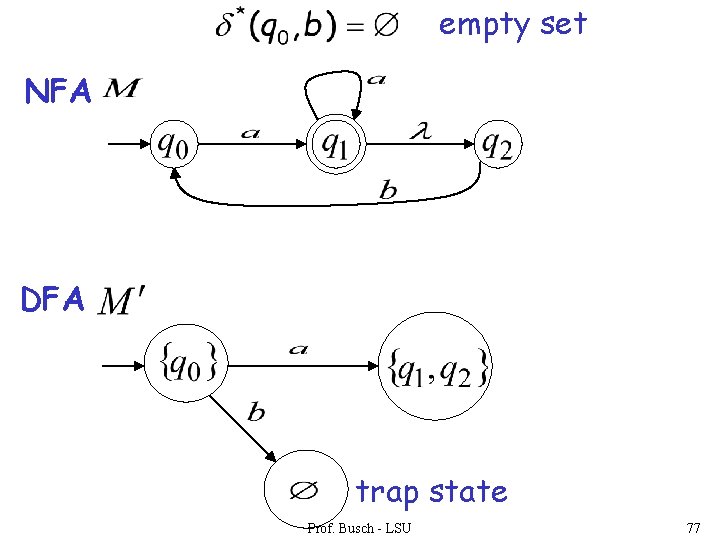
empty set NFA DFA trap state Prof. Busch - LSU 77

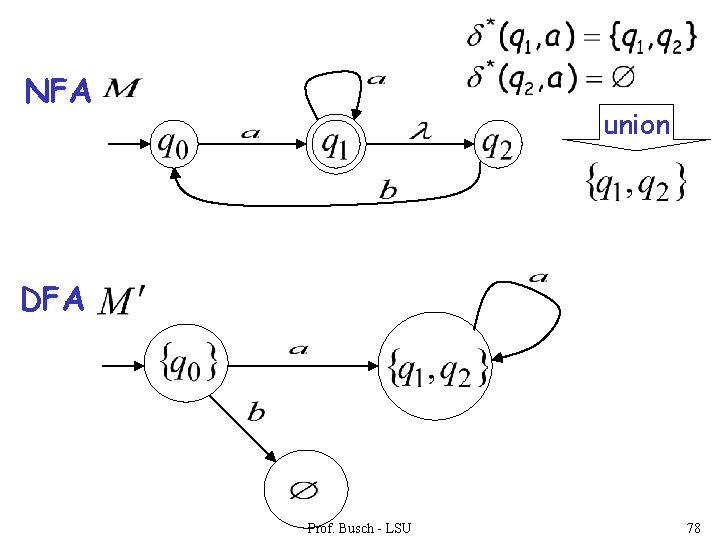
NFA union DFA Prof. Busch - LSU 78

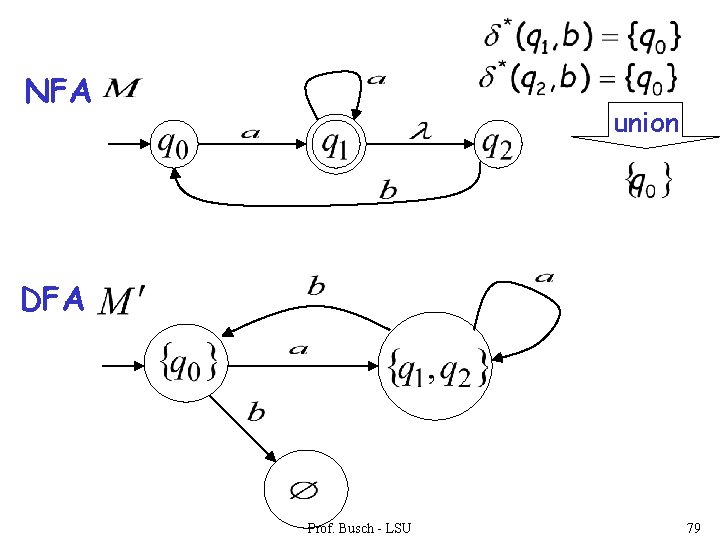
NFA union DFA Prof. Busch - LSU 79

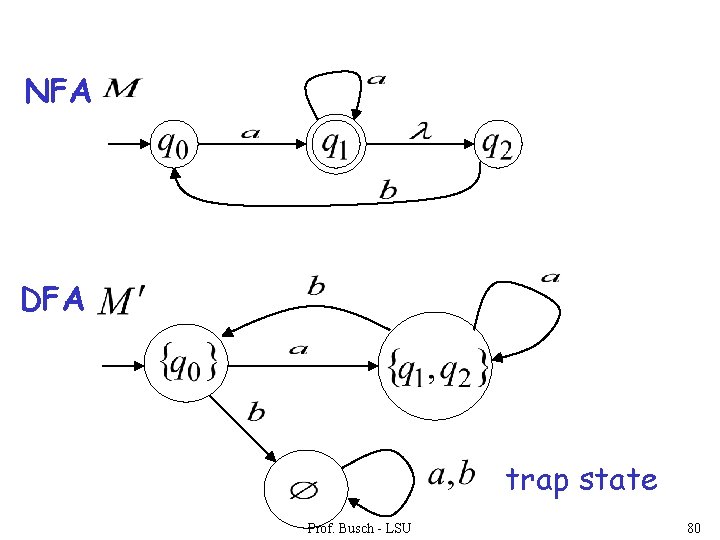
NFA DFA trap state Prof. Busch - LSU 80

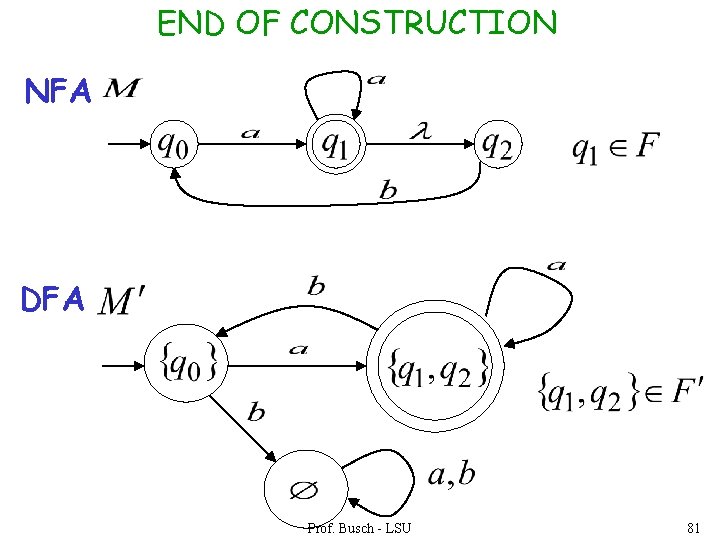
END OF CONSTRUCTION NFA DFA Prof. Busch - LSU 81

General Conversion Procedure Input: an NFA Output: an equivalent DFA with Prof. Busch - LSU 82

The NFA has states The DFA has states from the power set Prof. Busch - LSU 83

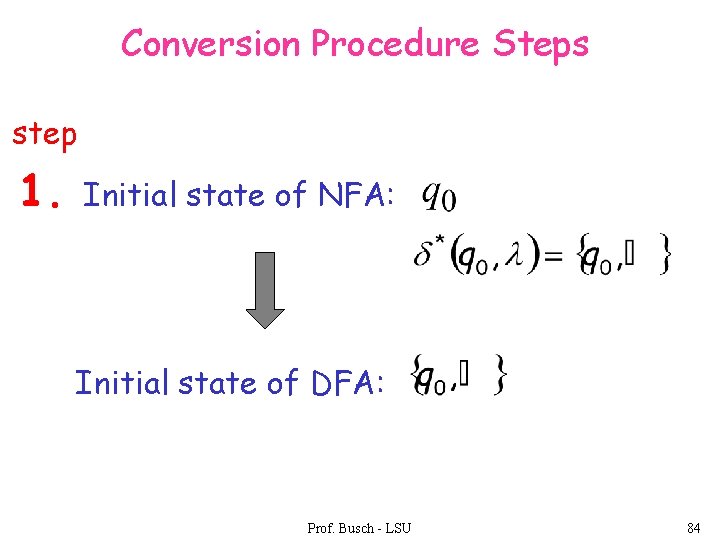
Conversion Procedure Steps step 1. Initial state of NFA: Initial state of DFA: Prof. Busch - LSU 84

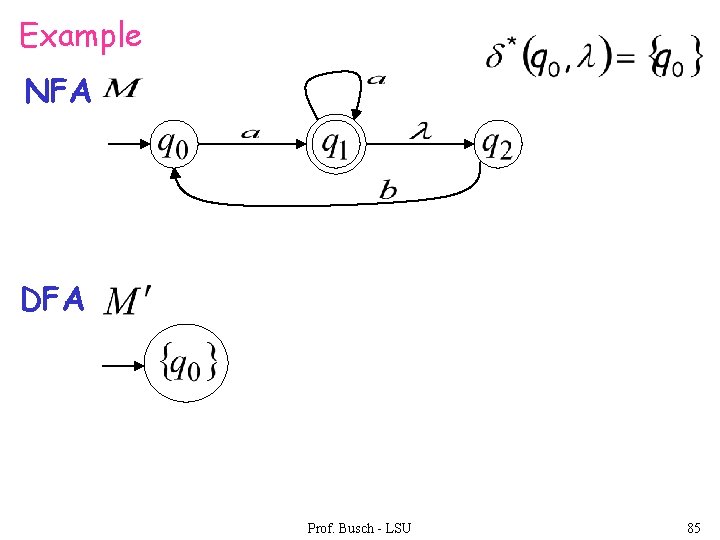
Example NFA DFA Prof. Busch - LSU 85

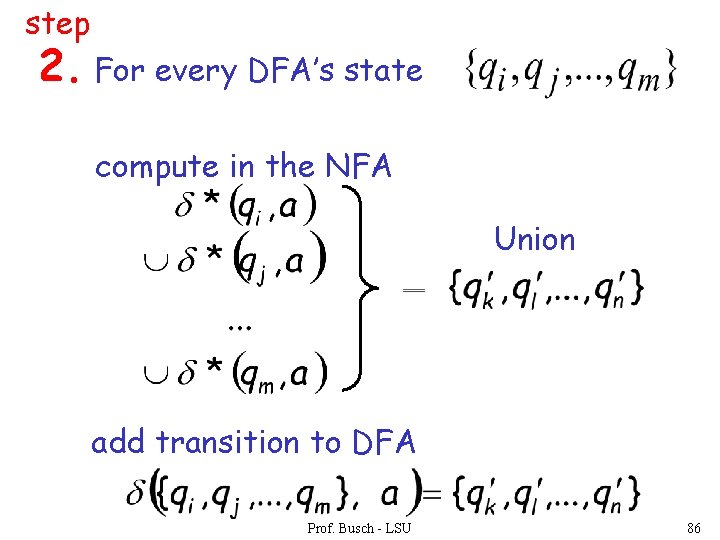
step 2. For every DFA’s state compute in the NFA Union add transition to DFA Prof. Busch - LSU 86

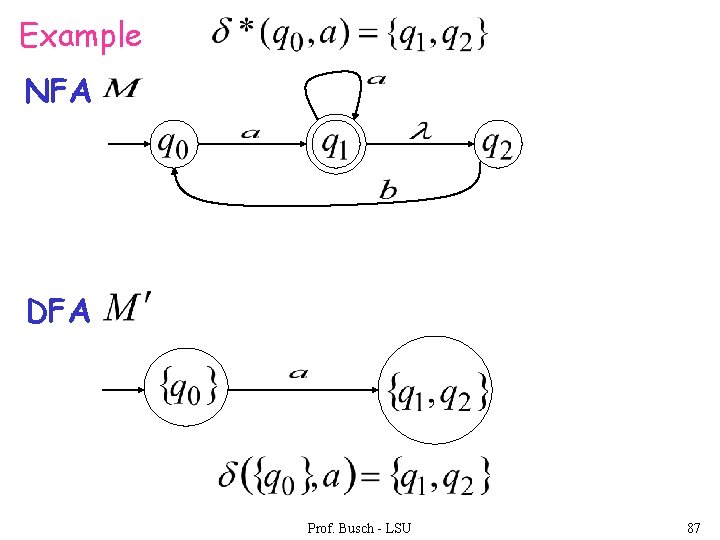
Example NFA DFA Prof. Busch - LSU 87

step 3. Repeat Step 2 for every state in DFA and symbols in alphabet until no more states can be added in the DFA Prof. Busch - LSU 88

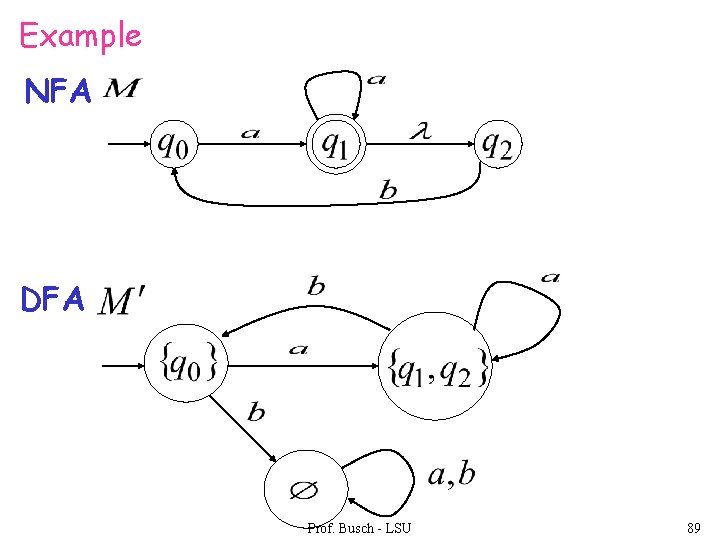
Example NFA DFA Prof. Busch - LSU 89

step 4. For any DFA state if some is accepting state in NFA Then, is accepting state in DFA Prof. Busch - LSU 90

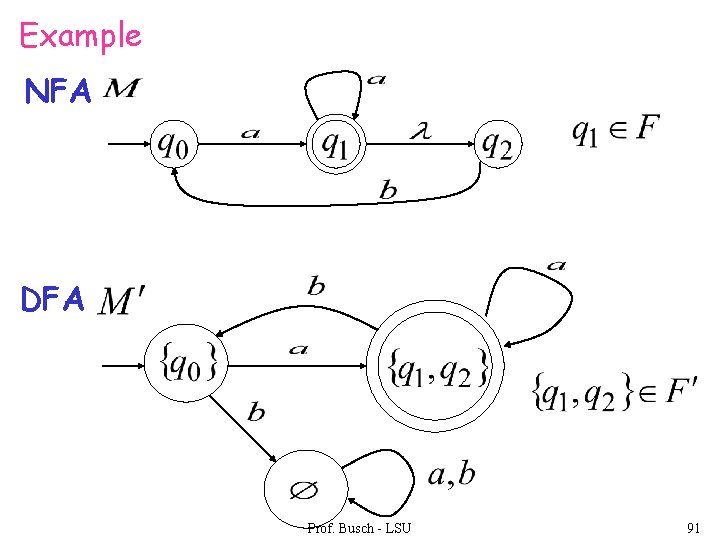
Example NFA DFA Prof. Busch - LSU 91

Lemma: If we convert NFA to DFA then the two automata are equivalent: Proof: We only need to show: AND Prof. Busch - LSU 92

First we show: We only need to prove: Prof. Busch - LSU 93

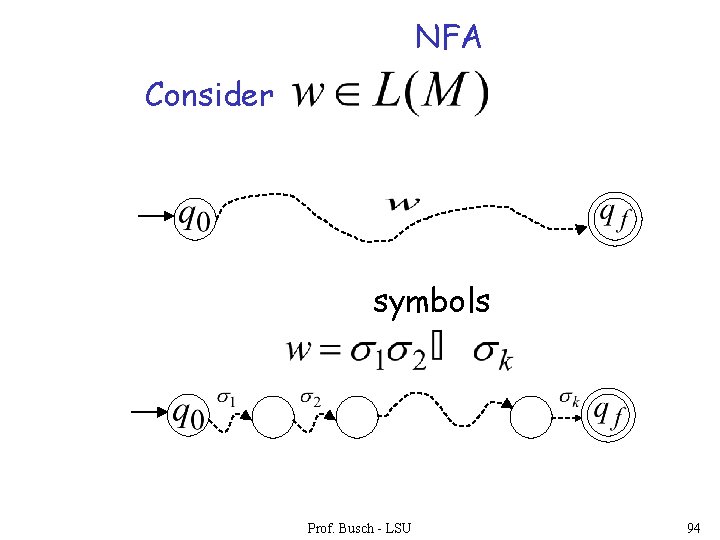
NFA Consider symbols Prof. Busch - LSU 94

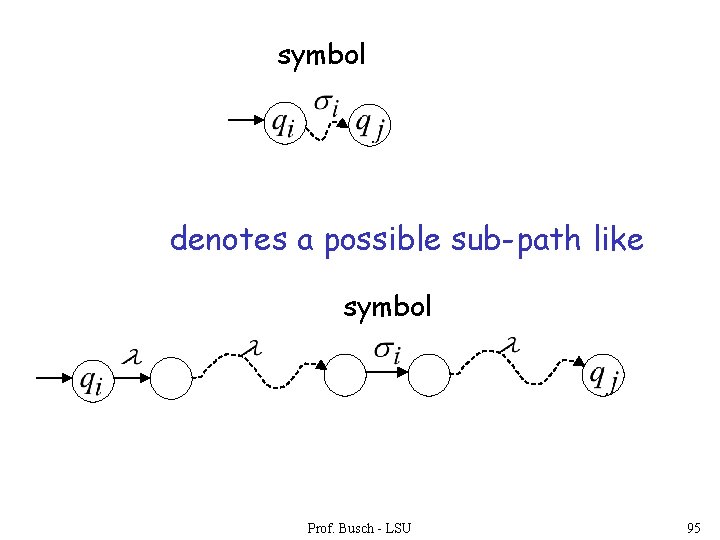
symbol denotes a possible sub-path like symbol Prof. Busch - LSU 95

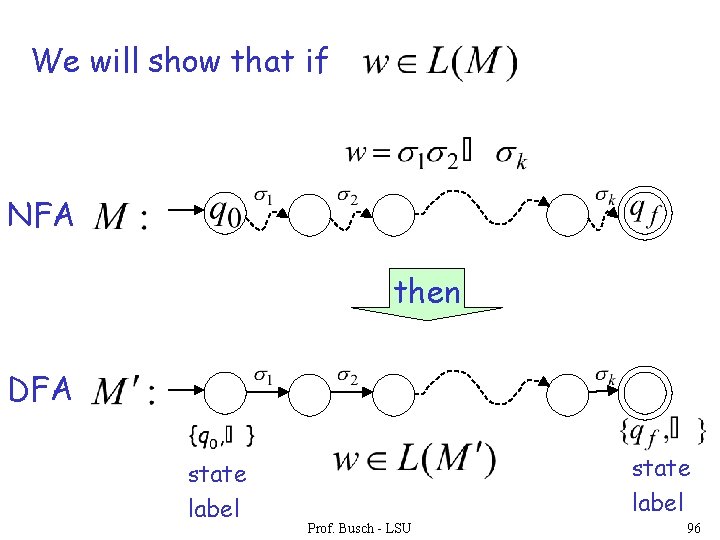
We will show that if NFA then DFA state label Prof. Busch - LSU 96

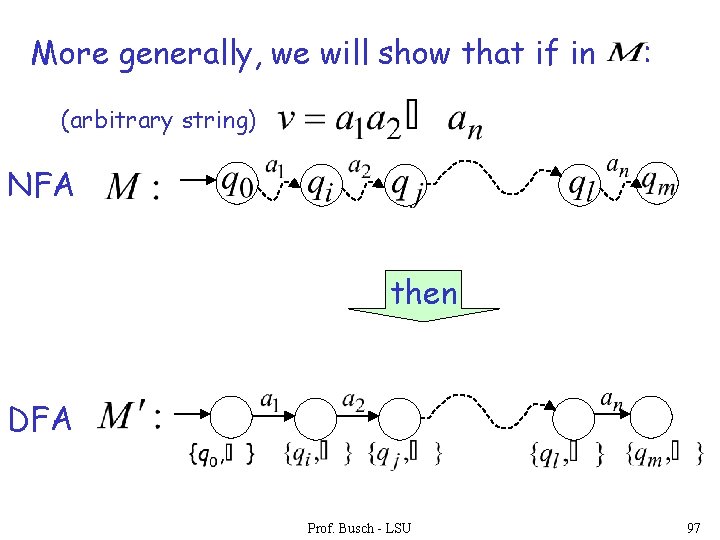
More generally, we will show that if in : (arbitrary string) NFA then DFA Prof. Busch - LSU 97

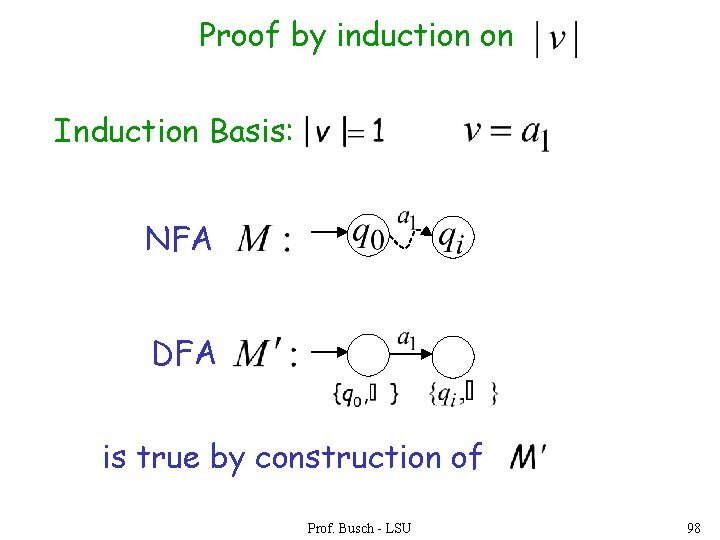
Proof by induction on Induction Basis: NFA DFA is true by construction of Prof. Busch - LSU 98

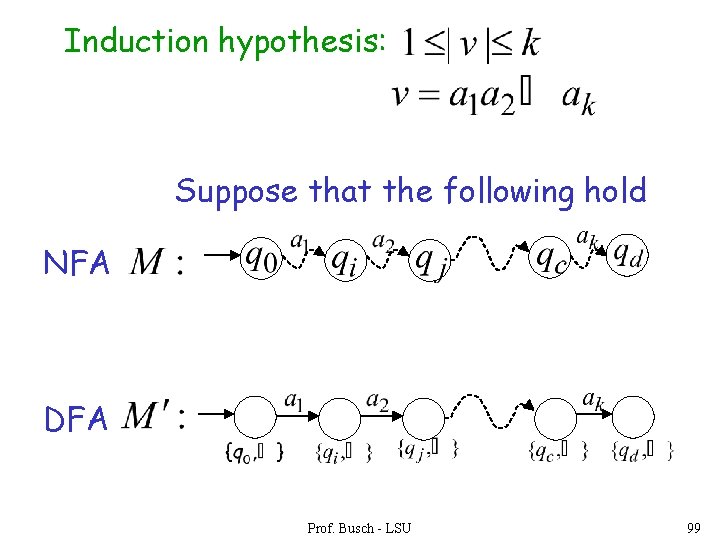
Induction hypothesis: Suppose that the following hold NFA DFA Prof. Busch - LSU 99

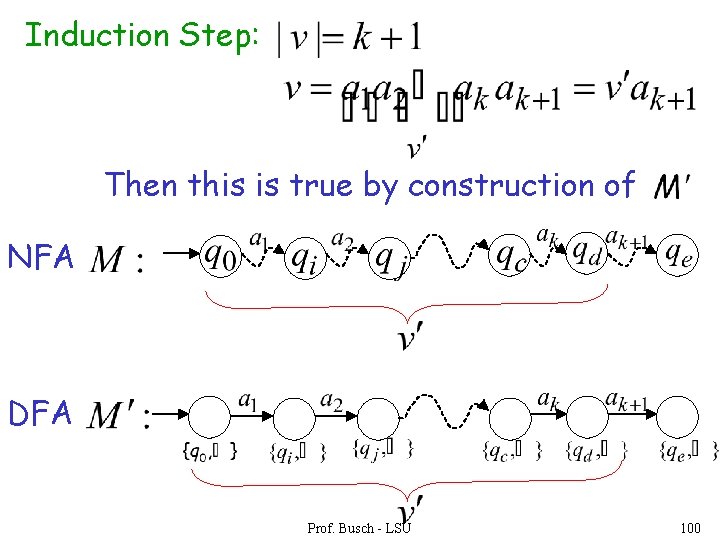
Induction Step: Then this is true by construction of NFA DFA Prof. Busch - LSU 100

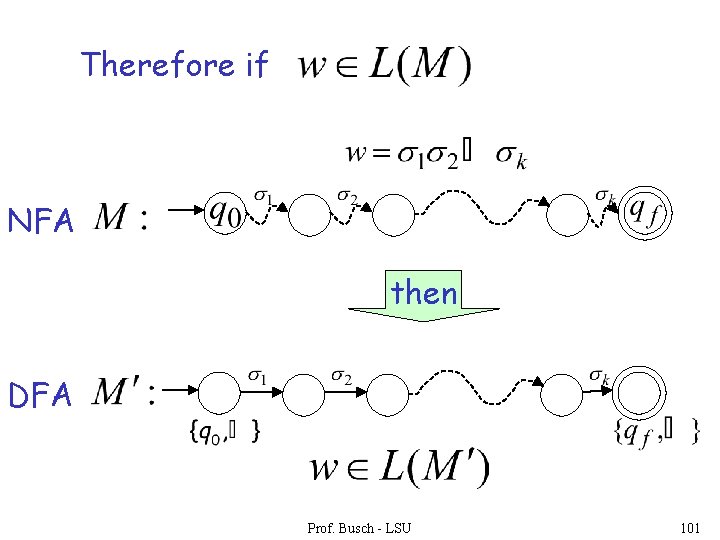
Therefore if NFA then DFA Prof. Busch - LSU 101

We have shown: With a similar proof we can show: Therefore: END OF LEMMA PROOF Prof. Busch - LSU 102