Advanced Automata Theory Neterministic Finite Automata nfa Lecture


















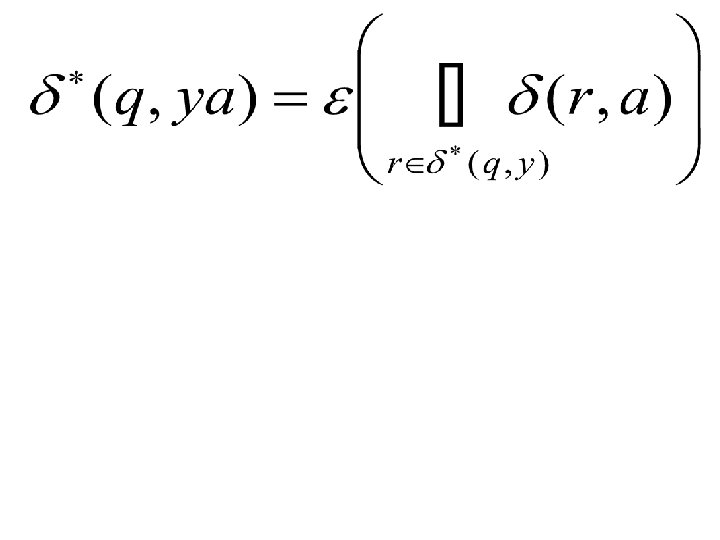


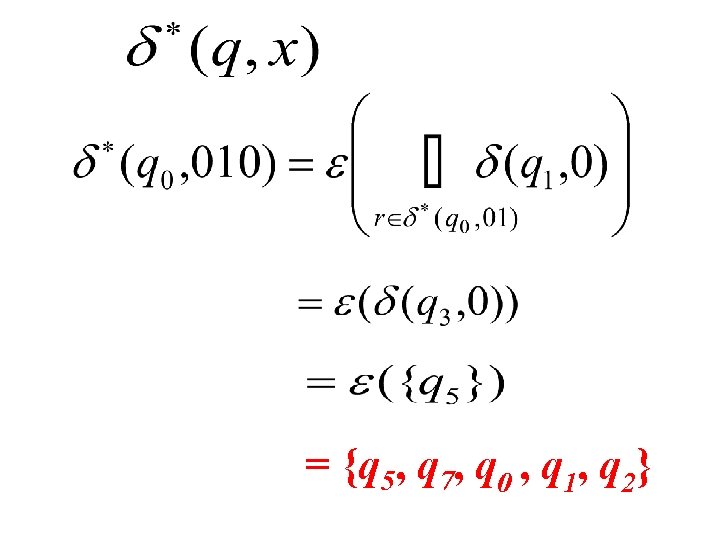





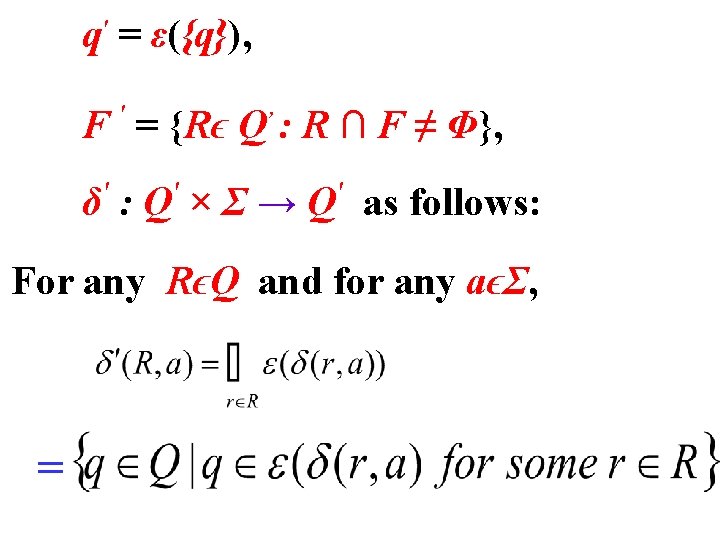






- Slides: 48

Advanced Automata Theory Neterministic Finite Automata (nfa) Lecture #9

Language & nfa

Let is be an nfa. The string accepted/recognized by M if The language accepted or recognized by M is the set L(M) of all strings accepted by M. For any language by M if L = L(M) is recognized

Examples

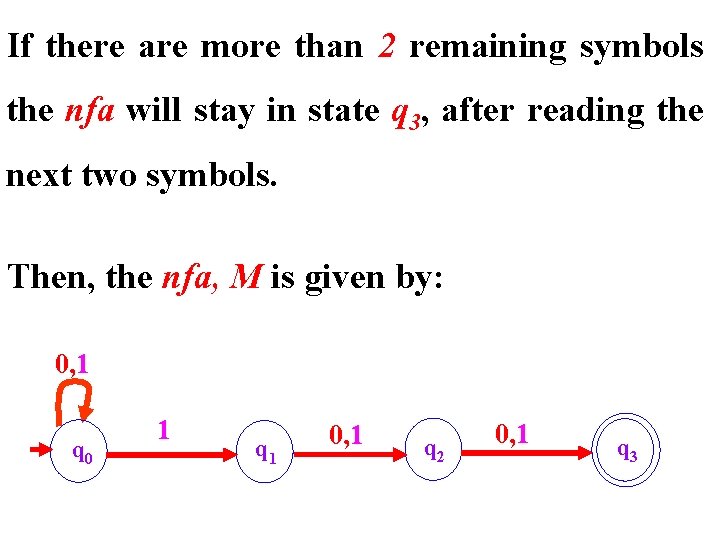
Example #1 Design an nfa for the following language L: The nfa does the following: If it is in the start state q 0 and reads the symbol 1, then it either stay in q 0 or guesses this symbol is the third symbol from the right in the input string

In the later case the nfa switches to state q 1, and then it verifies there are indeed two remaining symbols in the input string. This means the nfa switches to state q 2, and state q 3 (accept state) base on the next 2 input symbols (11) (from the input string).

If there are more than 2 remaining symbols the nfa will stay in state q 3, after reading the next two symbols. Then, the nfa, M is given by: 0, 1 q 0 1 q 1 0, 1 q 2 0, 1 q 3

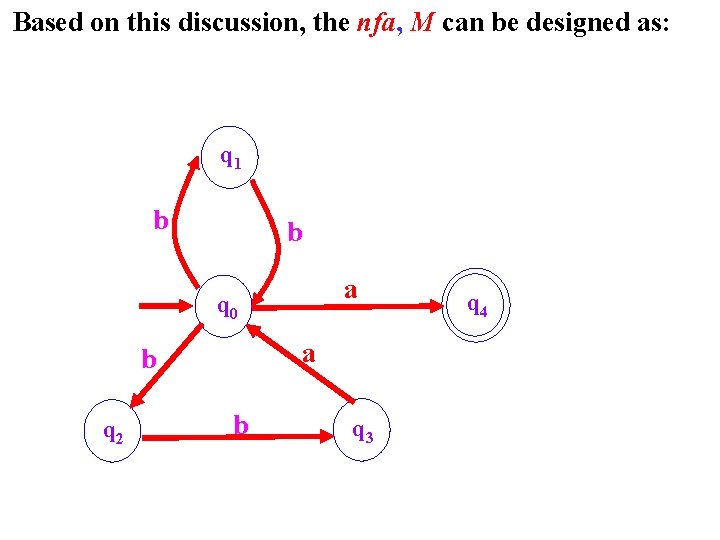
Example #2 Design an nfa for the following language L: The nfa does the following: If it is in the start state q 0 and reads the symbol a, it goes to state q 4 as final accepting state.

In state q 1, the machine read b it will go back to state q 0, after that if the machine encountered a then it will go to the final accepting state q 4, otherwise it will either goes to state q 1 or state q 2. At state q 2, if the machine encountered b it will go to state q 3. if the machine reads a at q 3 it will go to state q 0 and it there is one more symbol and it is an a, the machine will go to state q 4, so that string will be accepted.

Based on this discussion, the nfa, M can be designed as: q 1 b b a q 0 a b q 2 b q 3 q 4

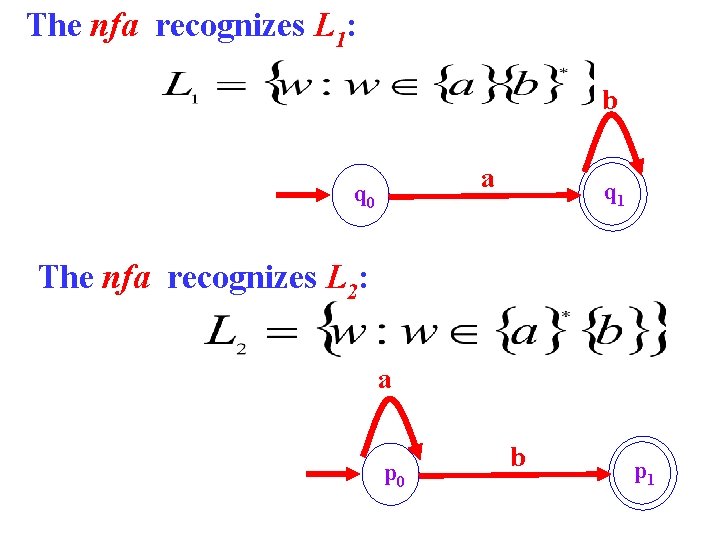
Example #3 Design nfas for the following languages L 1 and L 2, where Then, combine the two machines in one nfa that accepts L 1 and L 2.

The nfa recognizes L 1: b a q 0 q 1 The nfa recognizes L 2: a p 0 b p 1

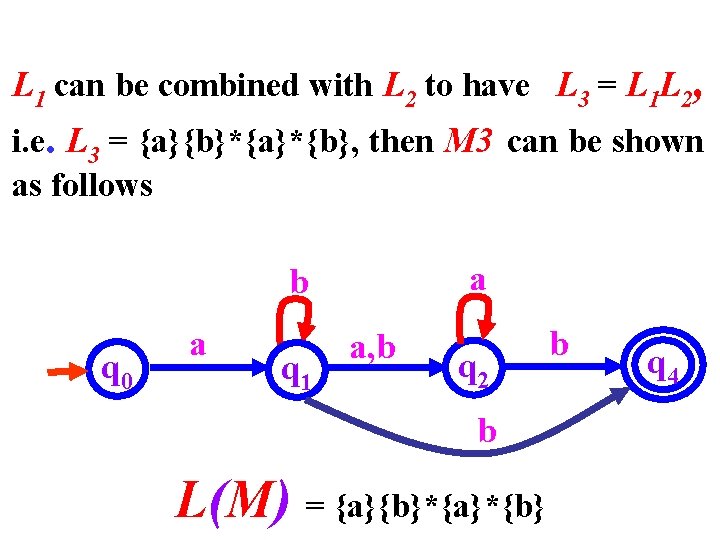
L 1 can be combined with L 2 to have L 3 = L 1 L 2, i. e. L 3 = {a}{b}*{a}*{b}, then M 3 can be shown as follows a b q 0 a q 1 a, b q 2 b L(M) = {a}{b}*{a}*{b} b q 4

nfa & Language

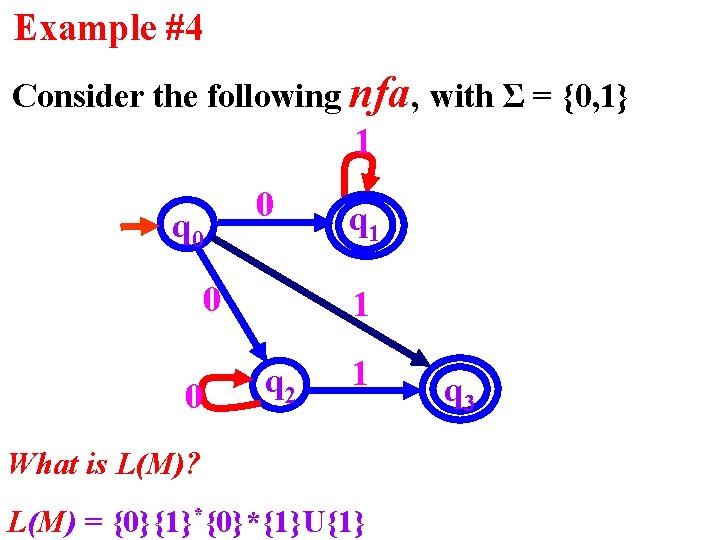
Example #4 Consider the following nfa, with Σ = {0, 1} 1 q 0 0 q 1 1 q 2 1 What is L(M)? L(M) = {0}{1}*{0}*{1}U{1} q 3

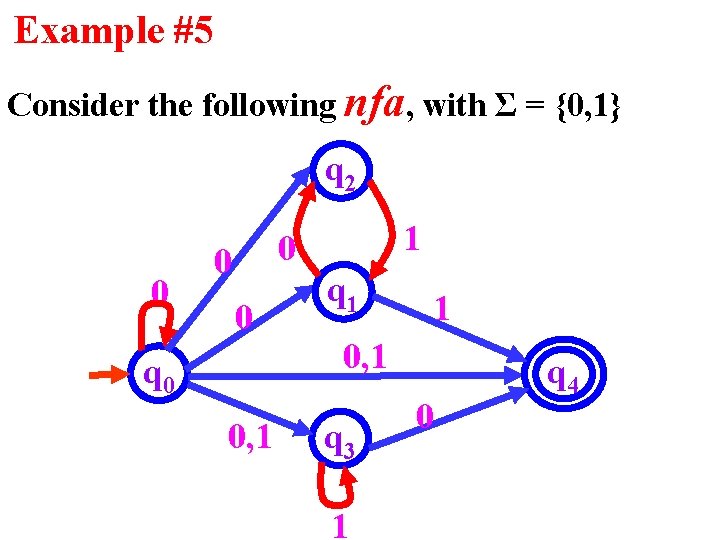
Example #5 Consider the following nfa, with Σ = {0, 1} q 2 0 1 0 0 0 q 0 0, 1 q 1 1 0, 1 q 3 1 0 q 4

What is the language that can be accepted/recognized by the nfa. ∩ L(M) = * * {0} {01} {1} * {1} {0}

Nondeterministic Finite Automata with transitions nfa-ε

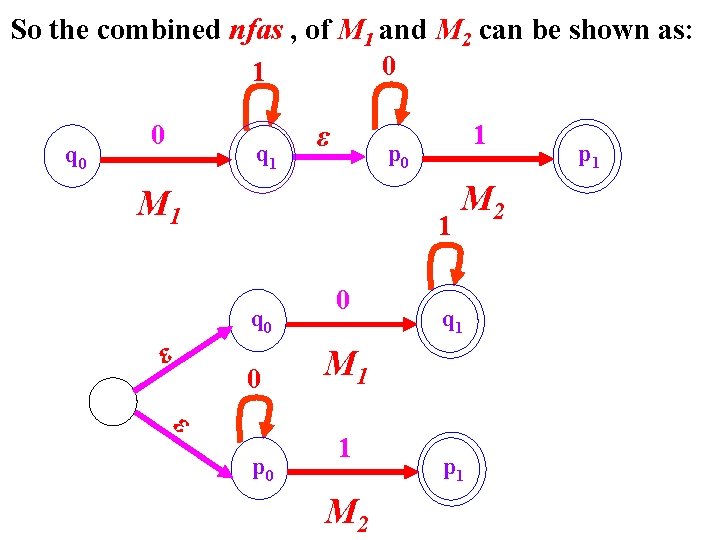
nfa. Let us consider the following two simple nfas , M 1 and M 2 that accepting the two languages: , respectively over the alphabet 1 q 0 0 M 1 q 1 0 p 0 1 M 2 p 1

Can the tow machines be combined into one machine M that accepting Concatenation of two the languages Union of two the languages The answer is yes only, we may need to add a new transition that doesn’t affect the behavior of the two machines, then comes the definition Nondeterministic Finite Automata, with which known as nfa- . of the transition,

So the combined nfas , of M 1 and M 2 can be shown as: 0 1 q 0 0 q 1 ε p 0 M 1 1 q 0 ε 1 0 ε p 0 0 M 2 q 1 M 1 1 M 2 p 1

Definition: nfa A nondeterministic finite automata nfa 5 -tuples : , where finite sets, and Same as for the nfa an extension of , is a are need to be defined for precise definition of accepting a string by nfa-

ε-closure of a set of states Let, and let S be subset of Q. the ε- closure of S is the set ε(S) defined as follows 1. Every elements of S is an element of ε(S); 2. 3. For any , every element of No other element of Q are in ε(S) is in

Algorithm to calculate ε(S) 1. Start with T = S. 2. Make a sequence of passes, in each pass considering and adding to T all elements of , that are not all ready in T. 3. Stop after any pass in which T does not change.

The definition of ε-closure help in defining recursively. Recursive definition of Let, be an nfa-ε. The function 1. For every 2. For every can be defined as:
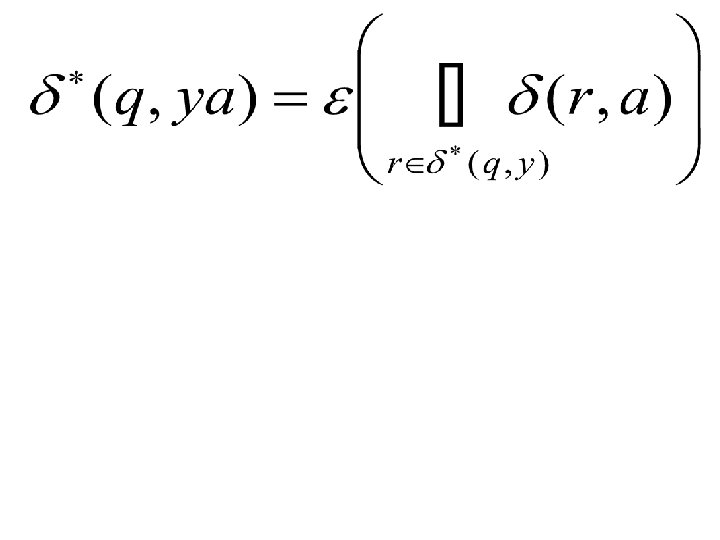

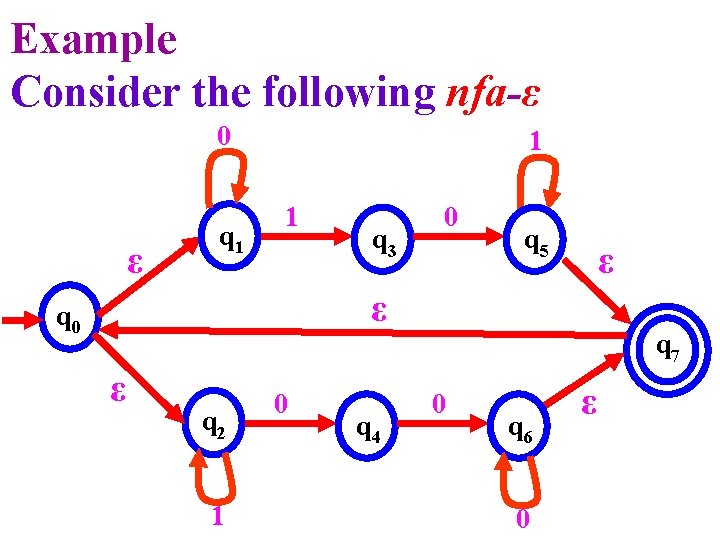
Example example Consider the following nfa-ε 0 ε q 1 1 1 q 3 0 q 5 ε ε q 0 ε q 2 1 0 q 4 q 7 0 q 6 0 ε

1. What is ε(S) if S = {q 5}? 2. What is if For the ε-closure, ε(S): After one iteration T = {q 5, q 7} After two iterations T = {q 5, q 7, q 0} After three iterations T = {q 5, q 7, q 0 , q 1, q 2}

In the next iteration there is no more change. Therefore, ε(S) = {q 5, q 7, q 0 , q 1, q 2}
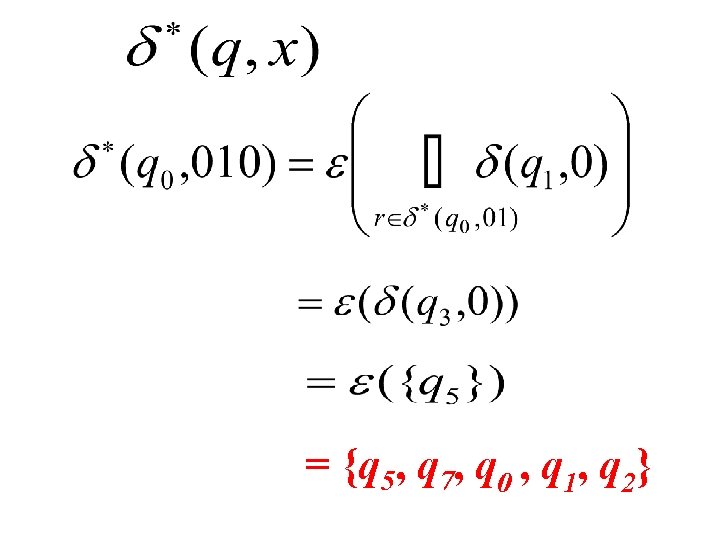
For = {q 5, q 7, q 0 , q 1, q 2}

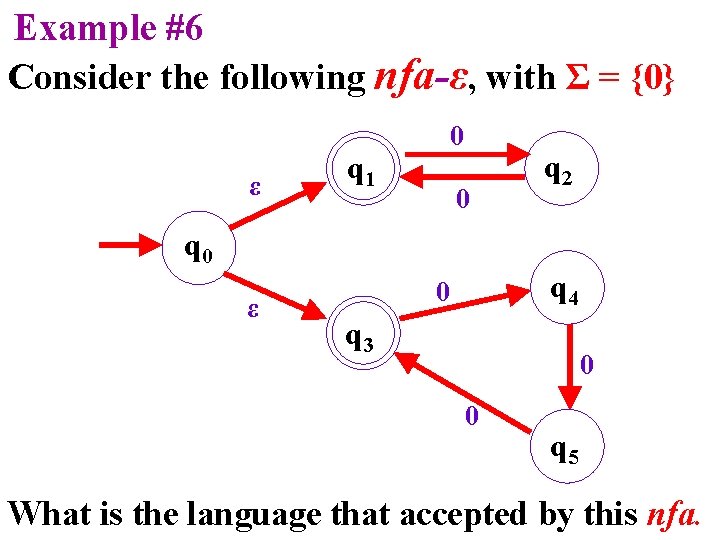
Example #6 Consider the following nfa-ε, with Σ = {0} ε q 1 0 0 q 2 q 0 ε q 4 0 q 3 0 0 q 5 What is the language that accepted by this nfa.

The language that accepted by this nfa: L(M) = k {0 | k is multiple of 2 or 3}

dfa vs. nfa • In a dfa, at every state , for every symbol , there is a unique –transition i. e. there is a unique such that . • This is not necessarily so in an nfa. At any state, an nfa may have multiple a- transitions, or none.

dfa vs. nfa • In a dfa, transition arrows are labeled by symbols from Σ; in an nfa, they are labeled by symbols from i. e. an nfa may have ε-transitions. • Non-determinism may be thought of as a kind of parallel computation where in several processes can be running concurrently.

Equivalence of dfa and nfa Every nfa has an equivalent dfa Let M = (Q, Σ, δ, q, F) be a nfa. There exist a dfa N, such that: L (M ) = L (N )

Conversion of a nfa to dfa The conversion can be carried out as follows: Let N = (Q, Σ, δ, q, F) be a nfa, an equivalent dfa, M can be defined as: M = (Q', Σ, δ', q', F'), where each component of M can be defined as: Q' = P(Q),
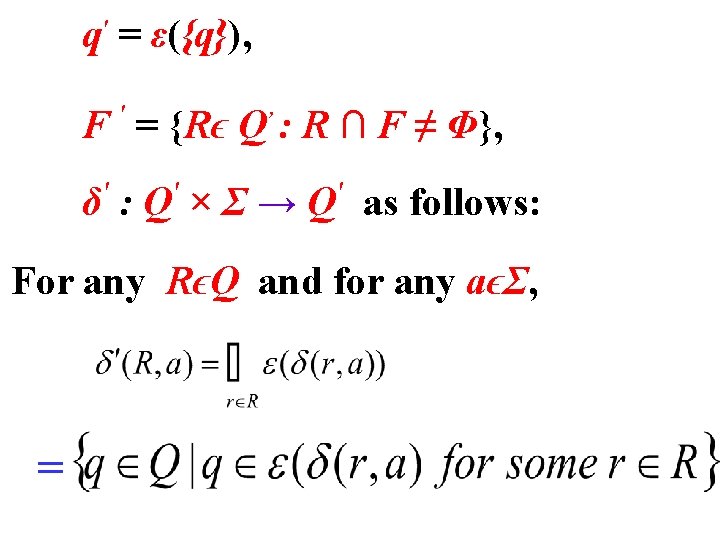

′ δ (R, a) is the set of all states that can be reached (in the nfa) by first following a transition labeled a from a state in R and then following 0 or more ε transitions

It can be concluded that, if A is a language, then A is regular iff there exist a ndf that accepts/recognizes A. , The equivalency can be shown through the state diagram of both M and N. Therefore L(M) = L(N).

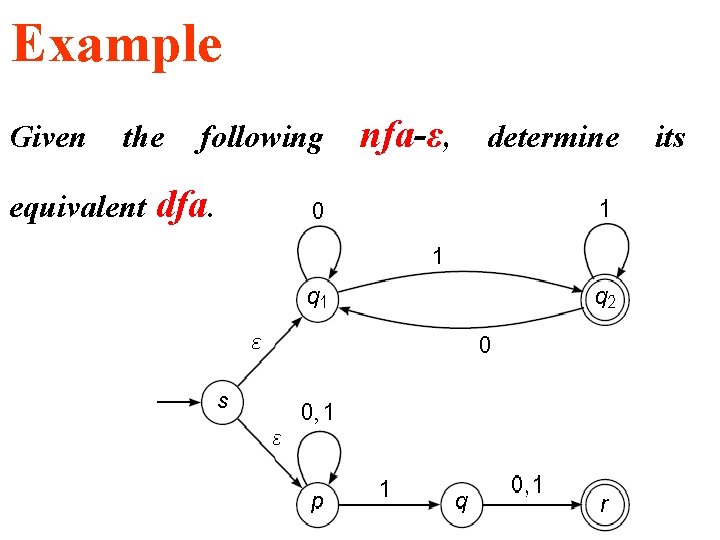
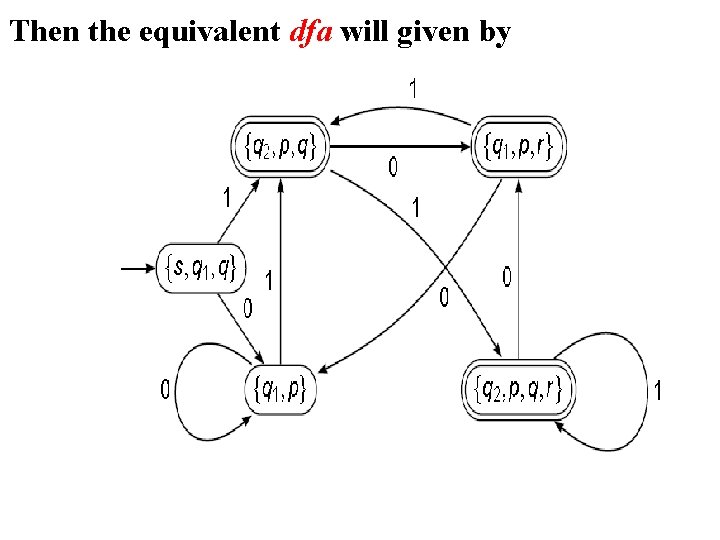
Example Given the equivalent following dfa. nfa-ε, determine its


Then the equivalent dfa will given by

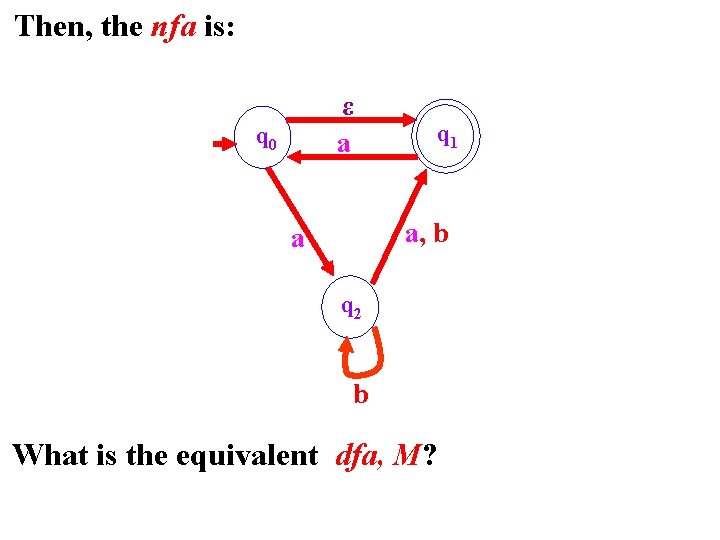
Example Consider the following nfa, N = (Q, Σ, δ, q, F), whose δ is given by: The state diagram for N can be shown as

Then, the nfa is: ε a q 0 q 1 a, b a q 2 b What is the equivalent dfa, M?

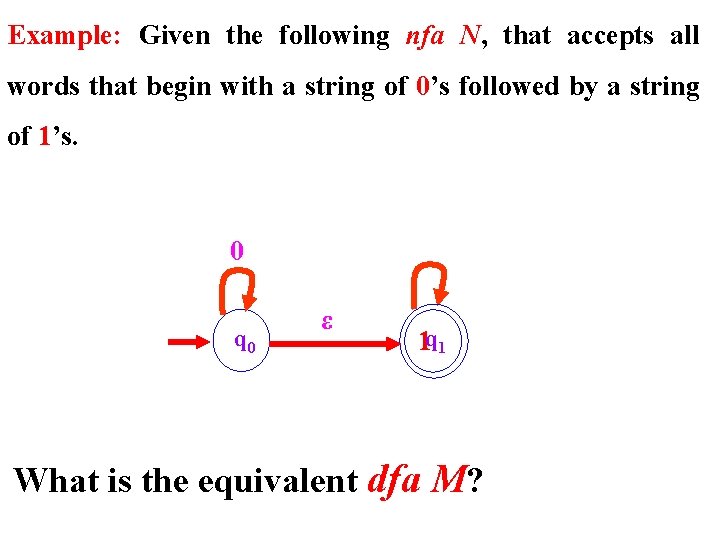
Example: Given the following nfa N, that accepts all words that begin with a string of 0’s followed by a string of 1’s. 0 q 0 ε 1 q 1 What is the equivalent dfa M?

Consider the following nfas N, with Σ = {0, 1} q 2 0 1 0 0 0 q 0 0, 1 q 1 1 0, 1 q 3 1 0 What are the equivalent dfa Ms? q 4

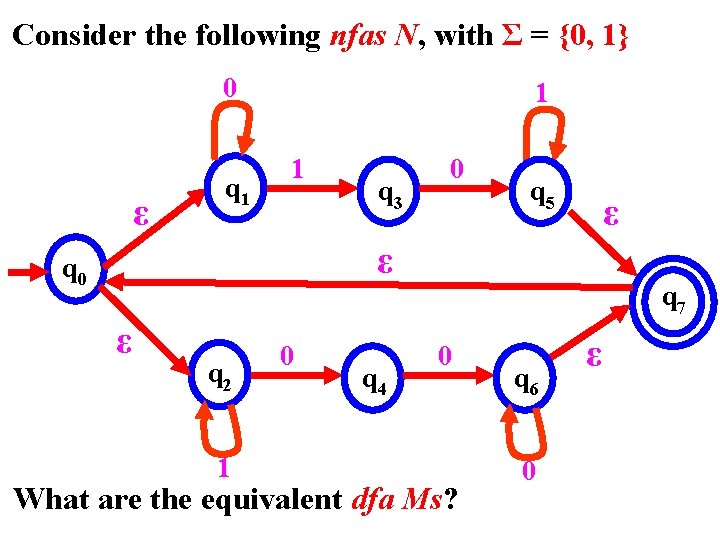
Consider the following nfas N, with Σ = {0, 1} 0 ε q 1 1 1 q 3 0 q 5 ε ε q 0 ε q 2 1 0 q 4 q 7 0 What are the equivalent dfa Ms? q 6 0 ε

Note: as general, nfas are more compact, they require fewer states to recognize a language compare to dfas.