Nondeterministic Finite Automata NFA Definition of an NFA

Nondeterministic Finite Automata (NFA) Definition of an NFA Testing string acceptance by NFA Construction of an equivalent DFA 1

Fundamental differences between NFA and DFA All FAs are a finite collection of states For DFAs, a unique state is occupied at any one time. For NFAs more one state can be occupied at one time. For DFA, d. D(q, a) is the unique state that become occupied when q is occupied and input a is processed For NFA, d. N(q, a) is a set of states that become occupied when q is occupied and input a is processed. Since the NFA may be in more than one state when input a is processed, we must get the union of d. N(qk, a) for all qk that are occupied when input a is processed. 2

Meaning of d. N(q, a)=nil d. N(q, a) defines a set of states that may be empty and denoted by nil. d. N(q, a)=nil means “terminate thread” that led to the current set of states, which includes q, occupied in the NFA when input a is processed. Any one of the occupied states for which d. N(q, a)=nil is sufficient to terminate thread. When a thread is terminated, occupied states with d. N(q, a) not equal to nil will create a new thread when input a is processed. This definition of d. N(q, a)=nil allows the rules of union of sets to be used when following the occupied states of an NFA as an input string is processed 3

Formal definition of NFA={Q, S, d, q 0, F} • Q = finite set of states • Σ = input alphabet • d = transition function is a set of states • Arguments are a state in Q and symbol in S • Returns subset of Q (could be empty) • q 0 = unique start state in Q • F ⊆ Q set of final states. 4

Extended Transition Function of NFA In δN(q, a), q is a state and a is a symbol but δN(q, a) is a set of states. Recursive definition delta hat Basis: d˄ (q, e) = {q}, d˄ (q, a) = δ(q, a) Induction: d˄ (q, xa) = the union of all states to which states in d˄ (q, x) go when input a is processed. 5

Language of an NFA 6

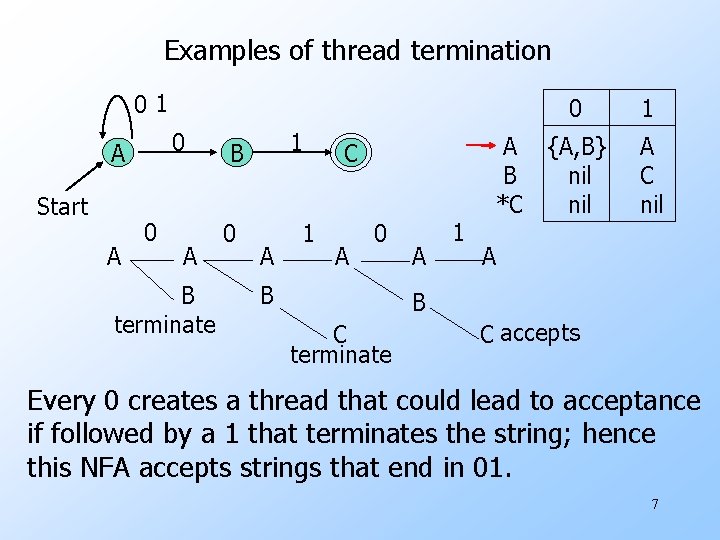
Examples of thread termination 01 0 A Start A 0 A B terminate 1 B 0 A 1 C A 0 B A 1 A B *C 0 1 {A, B} nil A C nil A B C terminate C accepts Every 0 creates a thread that could lead to acceptance if followed by a 1 that terminates the string; hence this NFA accepts strings that end in 01. 7

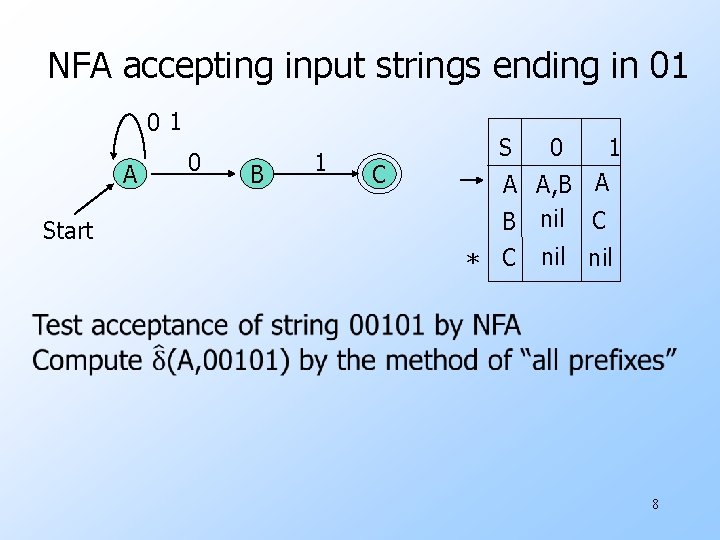
NFA accepting input strings ending in 01 01 A Start 0 B 1 C S 0 1 A A, B A B nil C * C nil 8

Test acceptance of string 00101 by NFA by the method of all prefixes S 0 1 A A, B A B nil C * C nil The normal use of nil in union of sets takes care of thread termination. 9

Test acceptance of string 00101 by NFA by the method of all prefixes S 0 1 A A, B A B nil C * C nil Note correspondence of nil with thread terminations in diagram below. 1 0 0 0 1 A A A B B B C C accepts 10

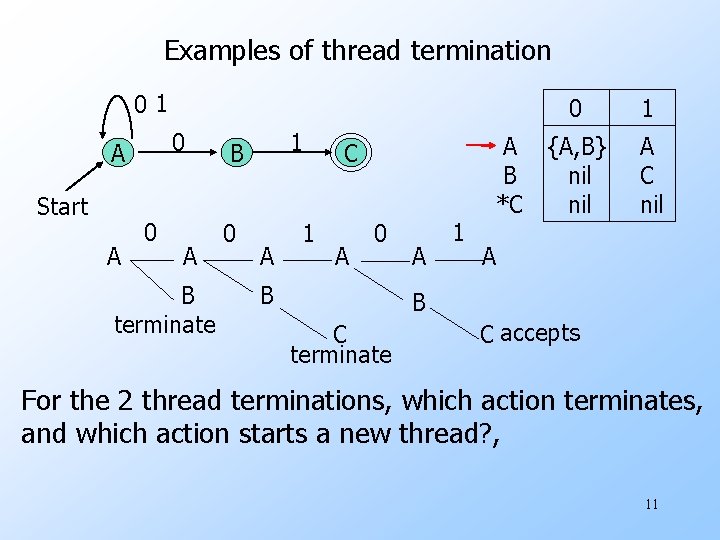
Examples of thread termination 01 0 A Start A 0 A B terminate 1 B 0 A 1 C A 0 B A 1 A B *C 0 1 {A, B} nil A C nil A B C terminate C accepts For the 2 thread terminations, which action terminates, and which action starts a new thread? , 11

Fundamental differences between NFA and DFA All FAs are a finite collection of states DFA is always in a unique state as input string is processed NFA can be in a set of states as input string is processed. For DFA, d. D(q, a) is the unique state that become occupied when q is occupied and input a is processed For NFA, d. N(q, a) is a set of states that become occupied when q is occupied and input a is processed. Since the NFA may be in more than one state when input a is processed, we must get the union of d. N(qk, a) for all qk that are occupied when input a is processed. 12

Test acceptance of string 001011 by NFA with transition function table using the method of all prefixes S 0 1 A A, B A B nil C * C nil ˄ d(A, e)={A} ˄d(A, 0)={A, B} ˄ d(A, 00)=d(A, 0) d(B, 0)={A, B} nil={A, B} ˄d(A, 001)=d(A, 1) d(B, 1)={A} {C}={A, C} ˄d(A, 0010)=d(A, 0) d(C, 0)={A, B} nil={A, B} ˄ d(A, 00101)=d(A, 1) d(B, 1) )={A} {C}={A, C} ˄ d(A, 001011)=d(A, 1) d(C, 1) )={A} nil={A} ˄ ˄ String rejected because set does not contain C 13

S 0 1 Test acceptance of string 011 by the A A, B A method of all prefixes. B nil C * C nil ˄ d(A, e)={A} ˄ d(A, 0)={A, B} ˄ d(A, 01)=d(A, 1) Ud(B, 1) = AUC = {A, C} ˄ d(A, 011)= d(A, 1)Ud(C, 1) = Aunil = A Rejected 14

15

From NFA to equivalent DFA • For any NFA there is an equivalent DFA that defines the same language. • Proof is by subset construction. We build the states and transition function of the equivalent DFA out of subsets of the states of the NFA. • If |QN|=n, then there are 2 n possible subsets of QN • Many of these subsets cannot be reached from the start state of the DFA, which is the same as the unique start state of the NFA. • Lazy subset construction just involves the reachable subsets of QN 16

Formal definition of equivalent DFA Given an NFA with states QN, alphabet Σ, transition function δN, start state q 0, and final states FN, construct equivalent DFA with the following rules: • States are among the subsets of QN • Same alphabet Σ as NFA • Same start state {q 0} • Final states = all subsets with a member in FN 17

Lazy subset construction of DFAeq • The “start” state of NFA is unique. Make it the singleton “start” subset of DFA. • Since DFA and NFA have the same “start” state, the 1 st rows of their respective transition tables must also be the same. • Add the subsets in the 1 st row of the DFA transition table to the states of the DFA and find where they go under transitions. • Every time δD({q 1, …, qk}, a) is a new subset, add it as a row in the d. D transition table. • δD({q 1, …, qk}, a) is the union over all i=1, …, k of δN(qi, a), where δN(qi, a) is the set of states that NFA goes to if it is in state qi and processes input character a. 18

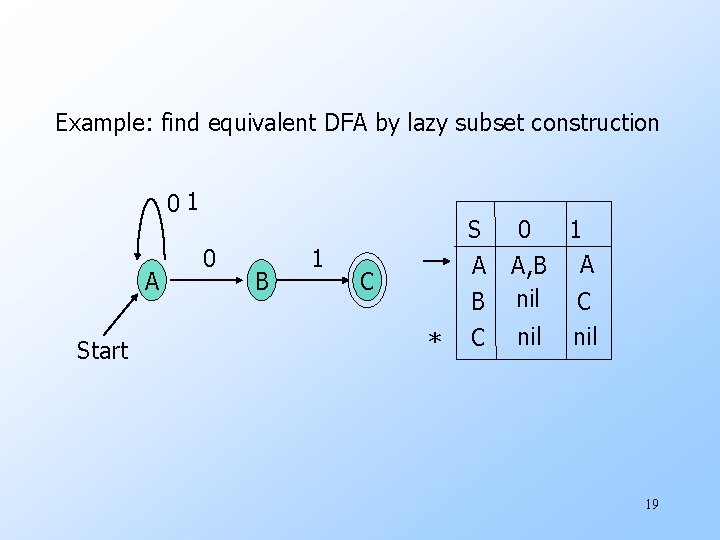
Example: find equivalent DFA by lazy subset construction 01 A Start 0 B 1 S C * A B C 0 1 A, B A nil C nil 19

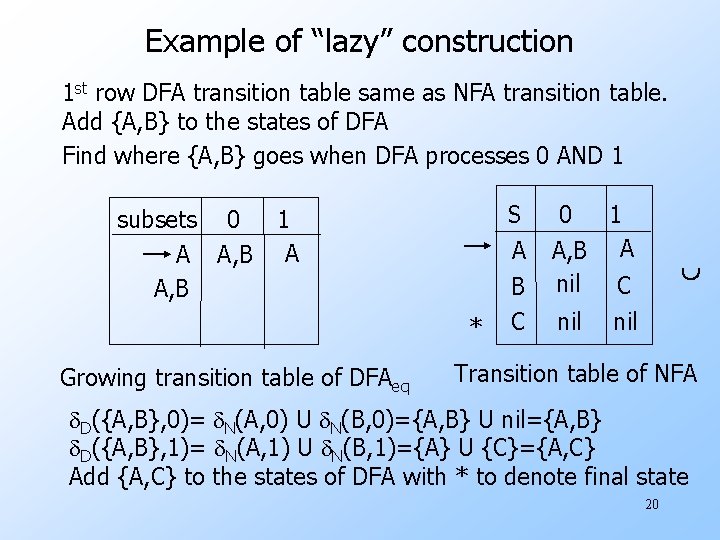
Example of “lazy” construction 1 st row DFA transition table same as NFA transition table. Add {A, B} to the states of DFA Find where {A, B} goes when DFA processes 0 AND 1 S subsets 0 1 A A, B * Growing transition table of DFAeq A B C 0 1 A, B A nil C nil Transition table of NFA d. D({A, B}, 0)= d. N(A, 0) U d. N(B, 0)={A, B} U nil={A, B} d. D({A, B}, 1)= d. N(A, 1) U d. N(B, 1)={A} U {C}={A, C} Add {A, C} to the states of DFA with * to denote final state 20

Example of “lazy” construction subsets 0 1 A A, B A, C * A, C Growing transition table of DFAeq S * A B C 0 1 A, B A nil C nil Transition table of NFA Find out where {A, C} goes under 0 and 1 d. D({A, C}, 0)= d. N(A, 0) U d. N(C, 0)={A, B} U nil={A, B} d. D({A, C}, 1)= d. N(A, 1) U d. N(C, 1)={A} U nil={A} No new subsets. We can complete DFA transition table 21

Example of “lazy” construction subsets 0 1 A A, B A, C * A, C A, B A We can rename the states of DFAeq q 0 =A q 1 ={A, B} q 2 ={A, C} Transition table of DFAeq States q 0 q 1 * q 2 0 q 1 q 1 1 q 0 q 2 q 0 Transition table of DFAeq with new state names. Graph and test acceptance of 101 by the definition of delta-hat 22

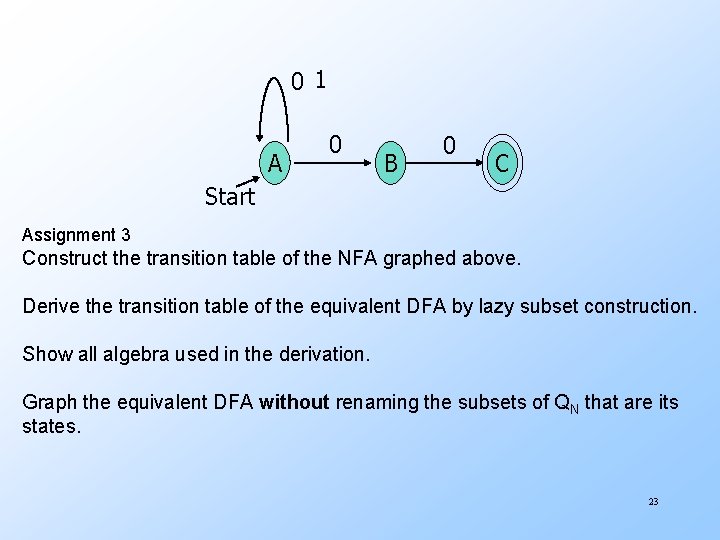
0 1 A 0 B 0 C Start Assignment 3 Construct the transition table of the NFA graphed above. Derive the transition table of the equivalent DFA by lazy subset construction. Show all algebra used in the derivation. Graph the equivalent DFA without renaming the subsets of QN that are its states. 23