Neural Network Verification Part 5 Complete Methods Neural

Neural Network Verification Part 5: Complete Methods

Neural Network Post. Verification Neural network f Scalar output z = f(x) E. g. in binary classification, z = s(y*; x) – s(y; x) for y ≠ y* Property: f(x) > 0 for all x ∈ X Complete methods try to disprove the property

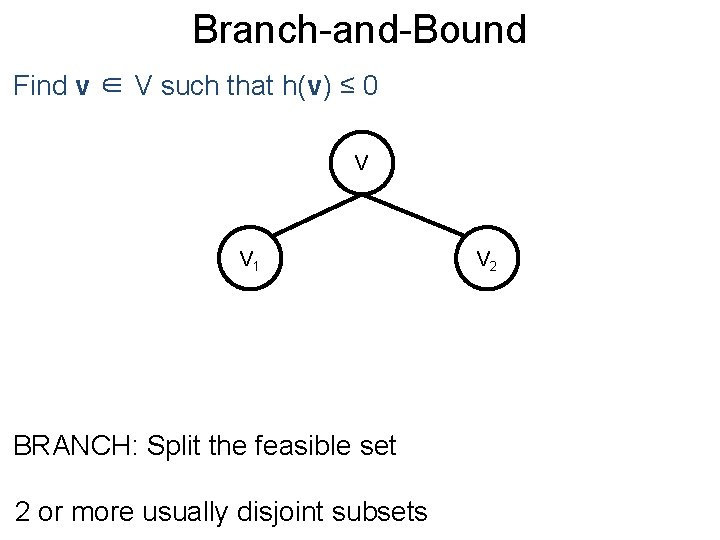
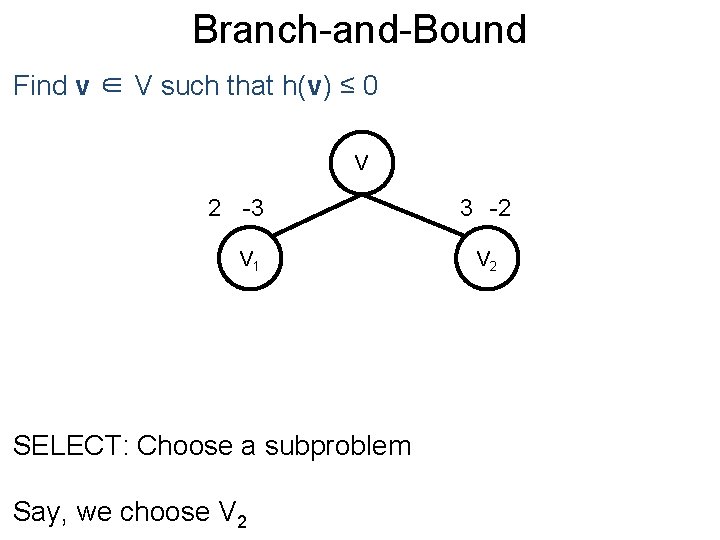
Branch-and-Bound Post Find v ∈ V such that h(v) ≤ 0 V V 1 BRANCH: Split the feasible set 2 or more usually disjoint subsets V 2

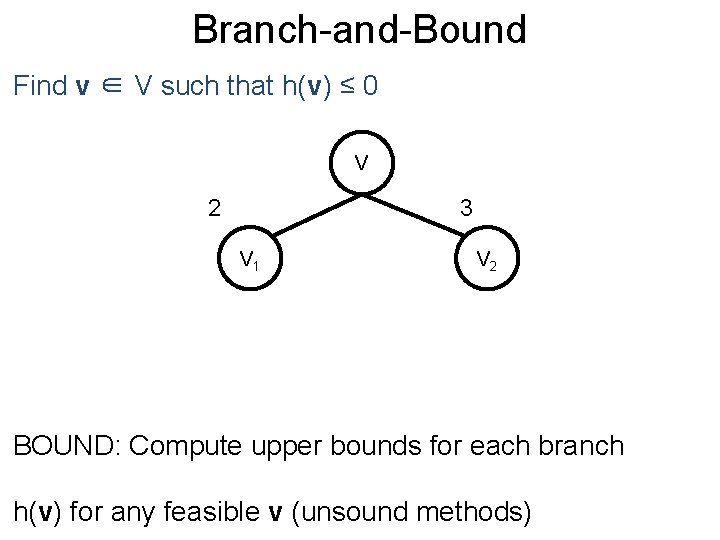
Branch-and-Bound Post Find v ∈ V such that h(v) ≤ 0 V 2 3 V 1 V 2 BOUND: Compute upper bounds for each branch h(v) for any feasible v (unsound methods)

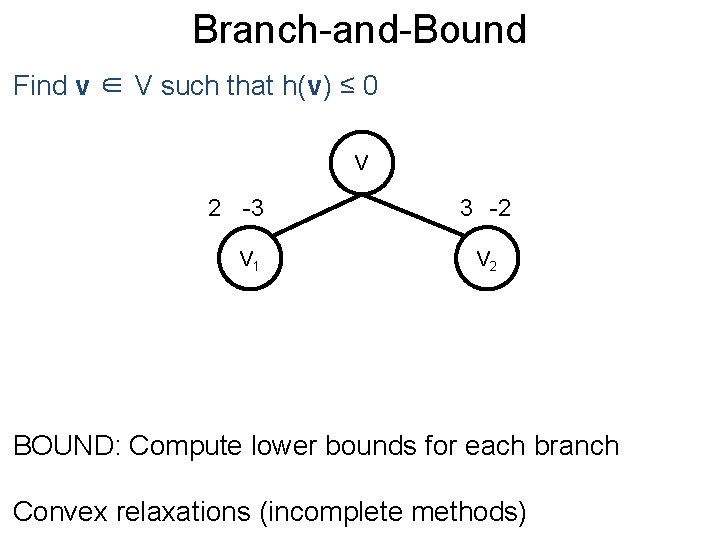
Branch-and-Bound Post Find v ∈ V such that h(v) ≤ 0 V 2 -3 V 1 3 -2 V 2 BOUND: Compute lower bounds for each branch Convex relaxations (incomplete methods)

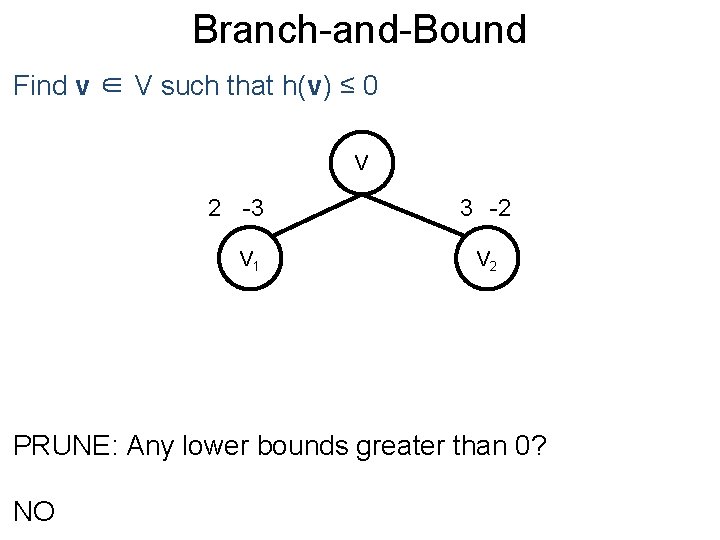
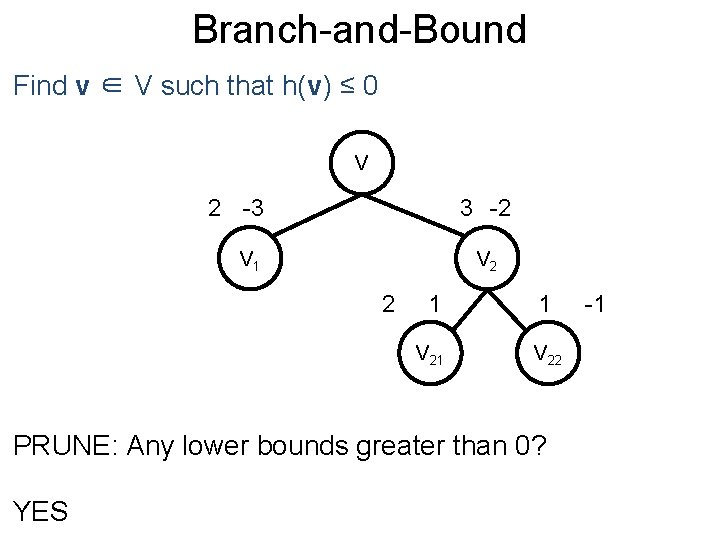
Branch-and-Bound Post Find v ∈ V such that h(v) ≤ 0 V 2 -3 V 1 3 -2 V 2 PRUNE: Any lower bounds greater than 0? NO

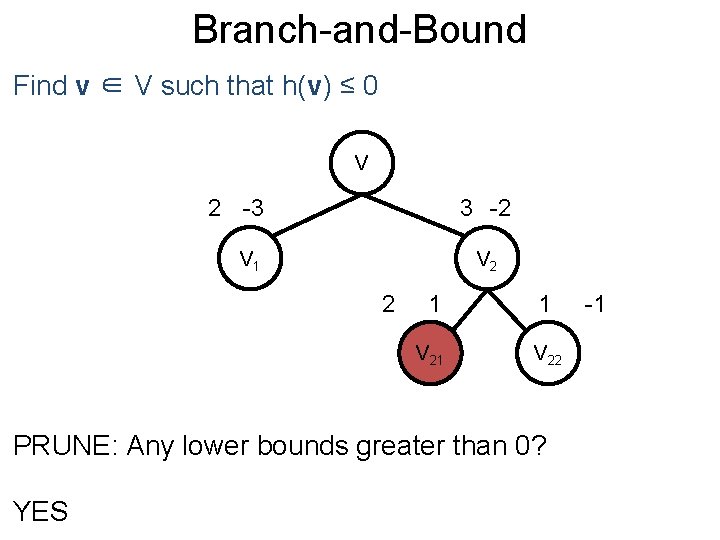
Branch-and-Bound Post Find v ∈ V such that h(v) ≤ 0 V 2 -3 V 1 SELECT: Choose a subproblem Say, we choose V 2 3 -2 V 2

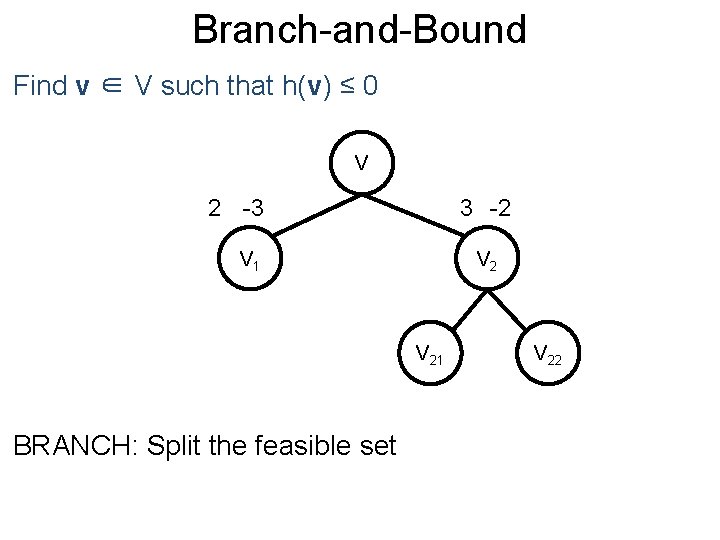
Branch-and-Bound Post Find v ∈ V such that h(v) ≤ 0 V 2 -3 3 -2 V 1 V 21 BRANCH: Split the feasible set V 22

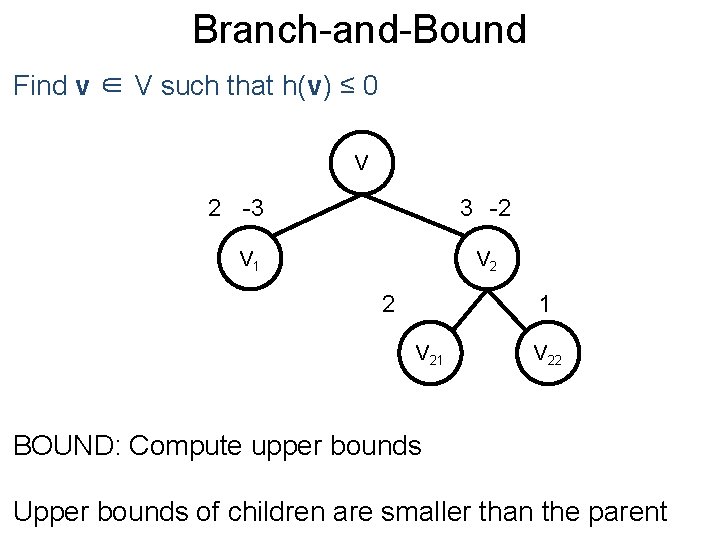
Branch-and-Bound Post Find v ∈ V such that h(v) ≤ 0 V 2 -3 3 -2 V 1 V 2 2 1 V 22 BOUND: Compute upper bounds Upper bounds of children are smaller than the parent

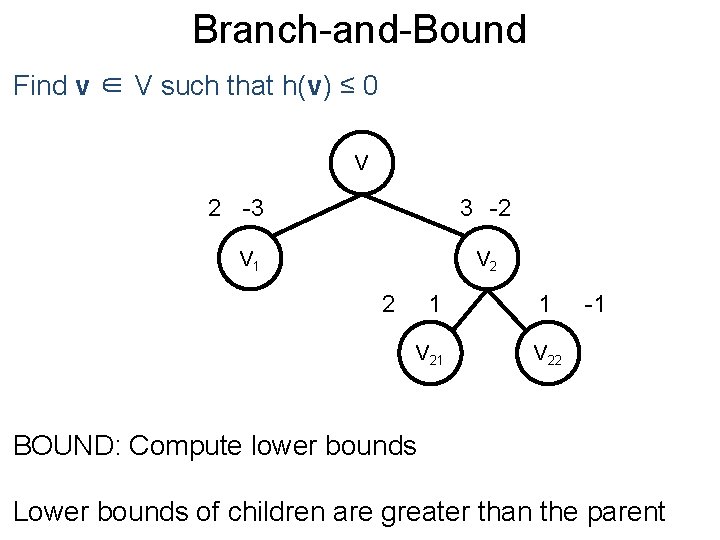
Branch-and-Bound Post Find v ∈ V such that h(v) ≤ 0 V 2 -3 3 -2 V 1 V 2 2 1 1 V 22 -1 BOUND: Compute lower bounds Lower bounds of children are greater than the parent

Branch-and-Bound Post Find v ∈ V such that h(v) ≤ 0 V 2 -3 3 -2 V 1 V 2 2 1 1 V 22 PRUNE: Any lower bounds greater than 0? YES -1

Branch-and-Bound Post Find v ∈ V such that h(v) ≤ 0 V 2 -3 3 -2 V 1 V 2 2 1 1 V 22 PRUNE: Any lower bounds greater than 0? YES -1

Branch-and-Bound Post Find v ∈ V such that h(v) ≤ 0 V 2 -3 3 -2 V 1 V 2 2 SELECT: Choose a subproblem Say, we choose V 1 1 1 V 22 -1

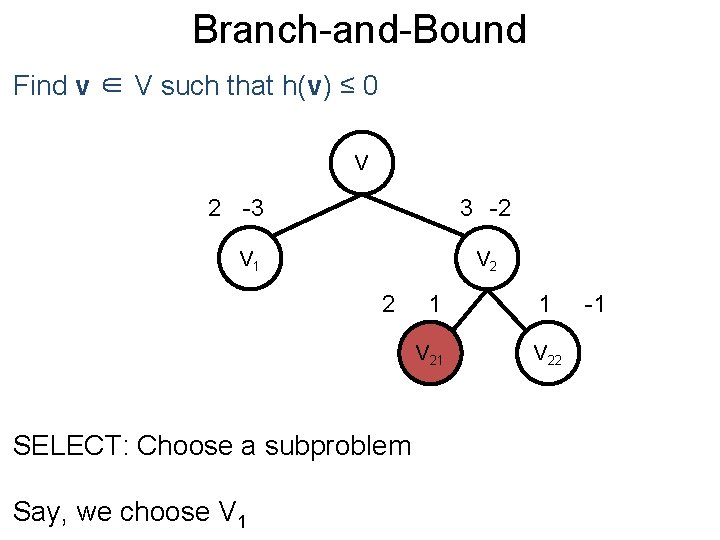
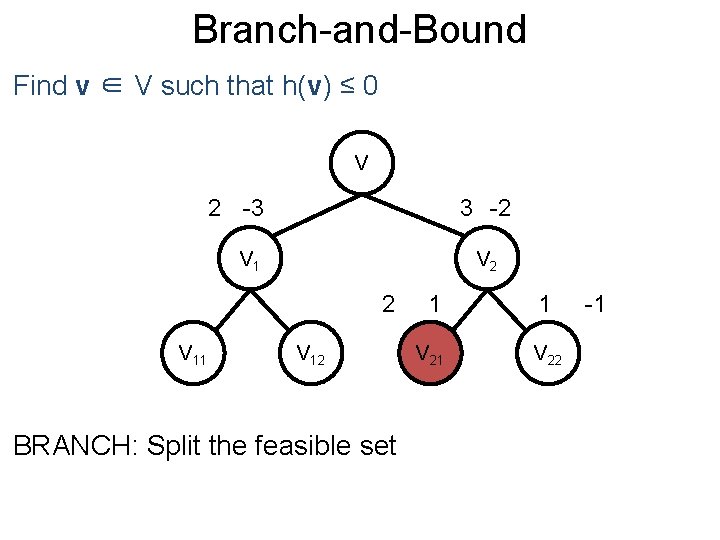
Branch-and-Bound Post Find v ∈ V such that h(v) ≤ 0 V 2 -3 3 -2 V 1 V 2 2 V 11 V 12 BRANCH: Split the feasible set 1 1 V 22 -1

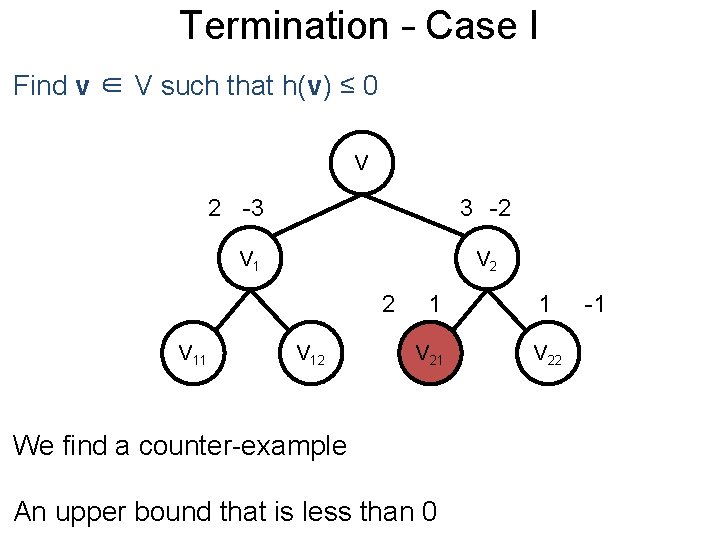
Termination Post– Case I Find v ∈ V such that h(v) ≤ 0 V 2 -3 3 -2 V 1 V 2 2 V 11 V 12 1 1 V 22 We find a counter-example An upper bound that is less than 0 -1

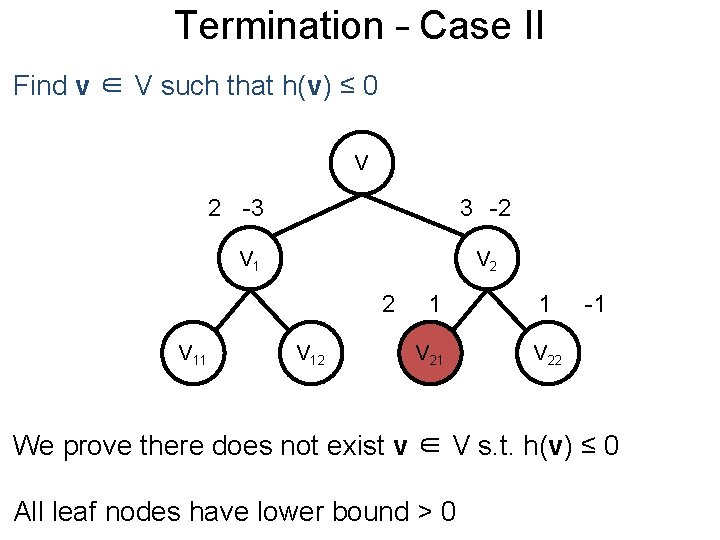
Termination Post– Case II Find v ∈ V such that h(v) ≤ 0 V 2 -3 3 -2 V 1 V 2 2 V 11 V 12 1 1 V 22 -1 We prove there does not exist v ∈ V s. t. h(v) ≤ 0 All leaf nodes have lower bound > 0

Unified. Post Framework All proposed complete methods are branch-and-bound Choice of branching Choice of bounding Choice of selecting (critical for false properties)

Outline • Reluplex • Planet • Input Domain Branch-and-Bound • Result Katz, Barrett, Dill, Julian and Kochendefer, 2017

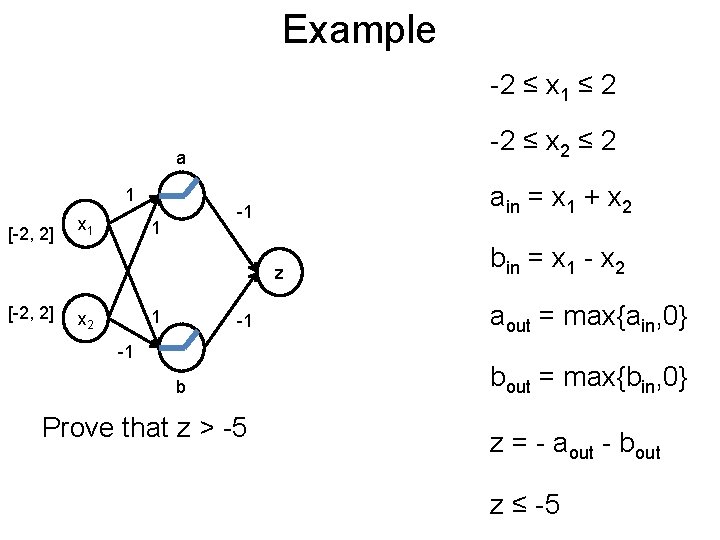
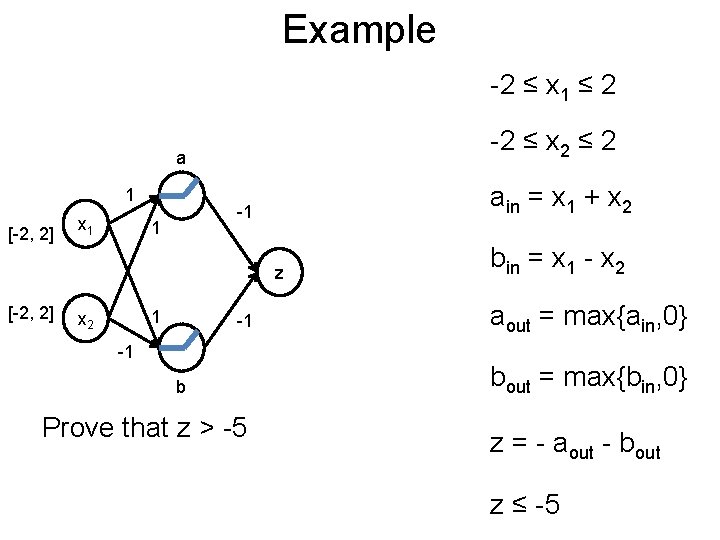
Example Post -2 ≤ x 1 ≤ 2 -2 ≤ x 2 ≤ 2 a 1 [-2, 2] x 1 ain = x 1 + x 2 -1 1 z [-2, 2] 1 x 2 -1 -1 b Prove that z > -5 bin = x 1 - x 2 aout = max{ain, 0} bout = max{bin, 0} z = - aout - bout z ≤ -5

Bounding Post x 1 x 2 ain aout bin bout z -2 ≤ x 1 ≤ 2 0 0 0 0 -2 ≤ x 2 ≤ 2 ain = x 1 + x 2 bin = x 1 - x 2 aout = max{ain, 0} bout = max{bin, 0} z = - aout - bout Infeasible z ≤ -5

Bounding Post x 1 x 2 ain aout bin bout z -2 ≤ x 1 ≤ 2 0 0 0 0 -2 ≤ x 2 ≤ 2 ain = x 1 + x 2 bin = x 1 - x 2 aout = max{ain, 0} bout = max{bin, 0} z = - aout - bout Relax all non-linearities z ≤ -5

Relaxation Post ain ∈ [l, u] aout = max{ain, 0} aout l Replace with convex superset u ain

Bounding Post x 1 x 2 ain aout bin bout z -2 ≤ x 1 ≤ 2 0 0 0 0 -2 ≤ x 2 ≤ 2 ain = x 1 + x 2 bin = x 1 - x 2 aout ≥ ain, aout ≥ 0, aout ≤ 4 bout ≥ bin, bout ≥ 0, bout ≤ 4 z = - aout - bout Relax all non-linearities z ≤ -5

Bounding Post x 1 x 2 ain aout bin bout z -2 ≤ x 1 ≤ 2 0 0 0 1 0 4 -5 -2 ≤ x 2 ≤ 2 ain = x 1 + x 2 bin = x 1 - x 2 aout ≥ ain, aout ≥ 0, aout ≤ 4 bout ≥ bin, bout ≥ 0, bout ≤ 4 z = - aout - bout z ≤ -5

Bounding Post x 1 x 2 ain aout bin bout z -2 ≤ x 1 ≤ 2 0 0 0 1 0 4 -5 -2 ≤ x 2 ≤ 2 ain = x 1 + x 2 bin = x 1 - x 2 aout = max{ain, 0} bout = max{bin, 0} z = - aout - bout Infeasible z ≤ -5

Bounding Post x 1 x 2 ain aout bin bout z -2 ≤ x 1 ≤ 2 0 0 0 1 0 4 -5 -2 ≤ x 2 ≤ 2 ain = x 1 + x 2 bin = x 1 - x 2 aout = max{ain, 0} bout = max{bin, 0} Fix a non-linearity (say b) Relax other non-linearities z = - aout - bout z ≤ -5

Bounding Post x 1 x 2 ain aout bin bout z -2 ≤ x 1 ≤ 2 0 0 0 1 0 4 -5 -2 ≤ x 2 ≤ 2 ain = x 1 + x 2 bin = x 1 - x 2 aout ≥ ain, aout ≥ 0, aout ≤ 4 bout = bin Fix a non-linearity (say b) Relax other non-linearities z = - aout - bout z ≤ -5

Bounding Post x 1 x 2 ain aout bin bout z -2 ≤ x 1 ≤ 2 2 -2 0 1 4 4 -5 -2 ≤ x 2 ≤ 2 ain = x 1 + x 2 bin = x 1 - x 2 aout ≥ ain, aout ≥ 0, aout ≤ 4 bout = bin z = - aout - bout z ≤ -5

Bounding Post x 1 x 2 ain aout bin bout z -2 ≤ x 1 ≤ 2 2 -2 0 1 4 4 -5 -2 ≤ x 2 ≤ 2 Repeat ain = x 1 + x 2 Try to fix some non-linearities bin = x 1 - x 2 Relax other non-linearities aout = max{ain, 0} bout = max{bin, 0} z = - aout - bout After some attempts, branch z ≤ -5

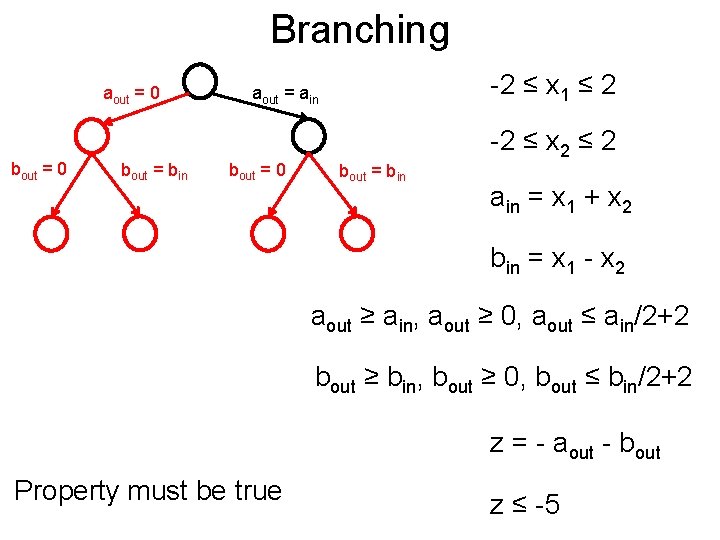
Branching Post -2 ≤ x 1 ≤ 2 -2 ≤ x 2 ≤ 2 ain = x 1 + x 2 Choose a non-linearity that is fixed many times bin = x 1 - x 2 aout = max{ain, 0} bout = max{bin, 0} z = - aout - bout z ≤ -5

Branching Post -2 ≤ x 1 ≤ 2 -2 ≤ x 2 ≤ 2 ain = x 1 + x 2 Choose a non-linearity that is fixed many times bin = x 1 - x 2 aout = max{ain, 0} Split into two bout = max{bin, 0} z = - aout - bout z ≤ -5

Branching Post -2 ≤ x 1 ≤ 2 -2 ≤ x 2 ≤ 2 ain = x 1 + x 2 bin = x 1 - x 2 aout = 0 aout = ain bout = max{bin, 0} z = - aout - bout z ≤ -5

Outline • Reluplex • Planet • Input Domain Branch-and-Bound • Result Ehlers, 2017

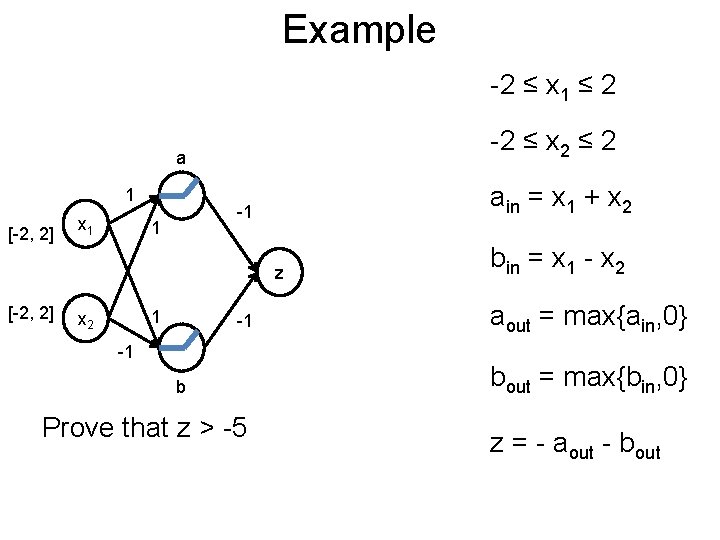
Example Post -2 ≤ x 1 ≤ 2 -2 ≤ x 2 ≤ 2 a 1 [-2, 2] x 1 ain = x 1 + x 2 -1 1 z [-2, 2] 1 x 2 -1 -1 b Prove that z > -5 bin = x 1 - x 2 aout = max{ain, 0} bout = max{bin, 0} z = - aout - bout z ≤ -5

Bounding Post -2 ≤ x 1 ≤ 2 -2 ≤ x 2 ≤ 2 ain = x 1 + x 2 bin = x 1 - x 2 aout = max{ain, 0} bout = max{bin, 0} z = - aout - bout Relax all non-linearities z ≤ -5

Relaxation Post ain ∈ [l, u] aout = max{ain, 0} aout l Replace with convex superset u ain

Bounding Post -2 ≤ x 1 ≤ 2 -2 ≤ x 2 ≤ 2 ain = x 1 + x 2 bin = x 1 - x 2 aout ≥ ain, aout ≥ 0, aout ≤ ain/2+2 bout ≥ bin, bout ≥ 0, bout ≤ bin/2+2 z = - aout - bout z ≤ -5

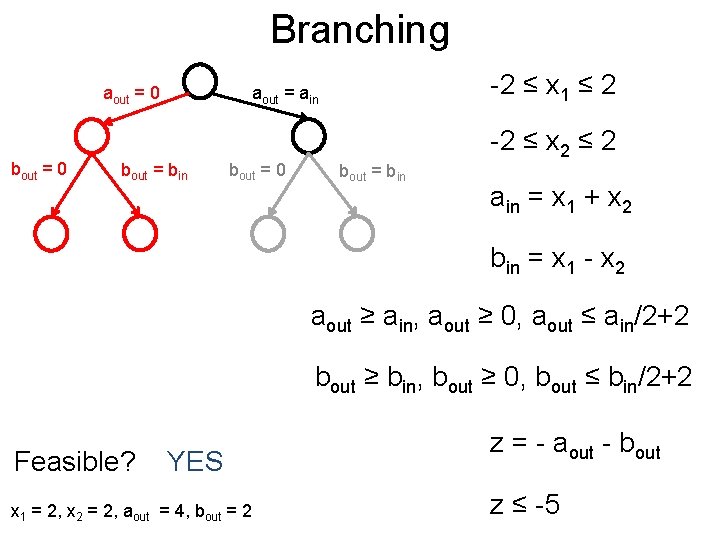
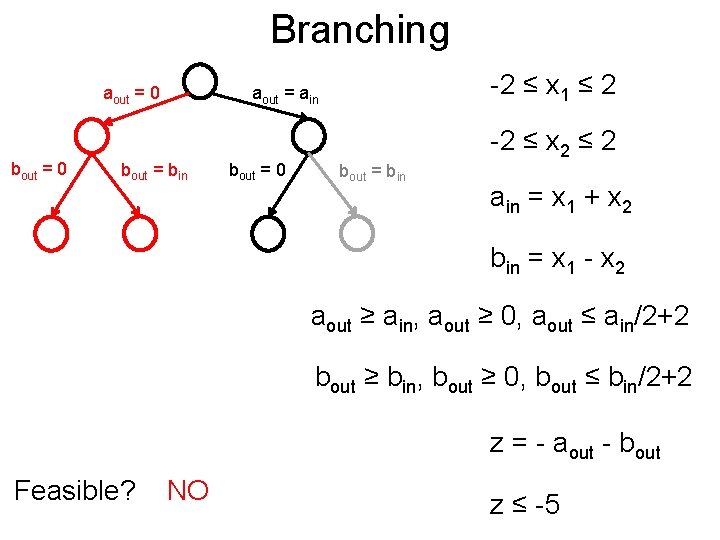
Branching Post aout = 0 bout = bin -2 ≤ x 1 ≤ 2 aout = ain bout = 0 bout = bin -2 ≤ x 2 ≤ 2 ain = x 1 + x 2 bin = x 1 - x 2 aout ≥ ain, aout ≥ 0, aout ≤ ain/2+2 bout ≥ bin, bout ≥ 0, bout ≤ bin/2+2 z = - aout - bout z ≤ -5

Branching Post aout = 0 bout = 0 -2 ≤ x 1 ≤ 2 aout = ain bout = bin bout = 0 bout = bin -2 ≤ x 2 ≤ 2 ain = x 1 + x 2 bin = x 1 - x 2 aout ≥ ain, aout ≥ 0, aout ≤ ain/2+2 bout ≥ bin, bout ≥ 0, bout ≤ bin/2+2 z = - aout - bout Feasible? NO z ≤ -5

Branching Post aout = 0 bout = bin -2 ≤ x 1 ≤ 2 aout = ain bout = 0 bout = bin -2 ≤ x 2 ≤ 2 ain = x 1 + x 2 bin = x 1 - x 2 aout ≥ ain, aout ≥ 0, aout ≤ ain/2+2 bout ≥ bin, bout ≥ 0, bout ≤ bin/2+2 z = - aout - bout Prune away z ≤ -5

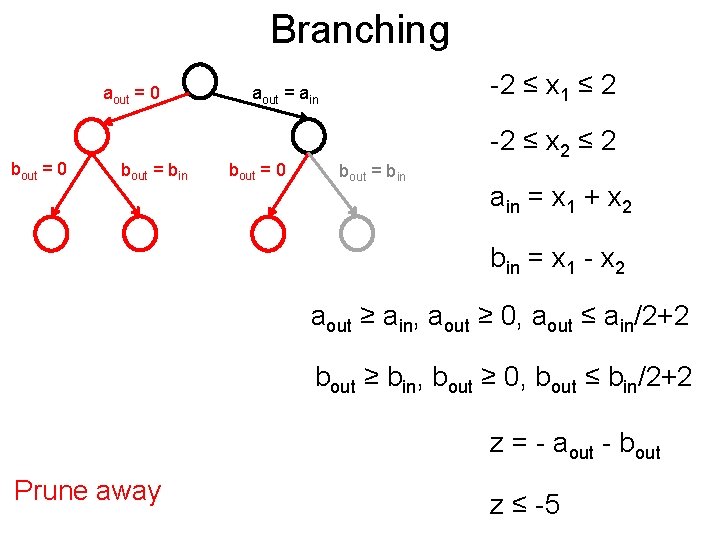
Branching Post aout = 0 bout = 0 -2 ≤ x 1 ≤ 2 aout = ain bout = bin bout = 0 bout = bin -2 ≤ x 2 ≤ 2 ain = x 1 + x 2 bin = x 1 - x 2 aout ≥ ain, aout ≥ 0, aout ≤ ain/2+2 bout ≥ bin, bout ≥ 0, bout ≤ bin/2+2 Feasible? YES x 1 = 2, x 2 = 2, aout = 4, bout = 2 z = - aout - bout z ≤ -5

Branching Post aout = 0 bout = 0 -2 ≤ x 1 ≤ 2 aout = ain bout = bin bout = 0 bout = bin -2 ≤ x 2 ≤ 2 ain = x 1 + x 2 bin = x 1 - x 2 aout ≥ ain, aout ≥ 0, aout ≤ ain/2+2 bout ≥ bin, bout ≥ 0, bout ≤ bin/2+2 z = - aout - bout Feasible? NO z ≤ -5

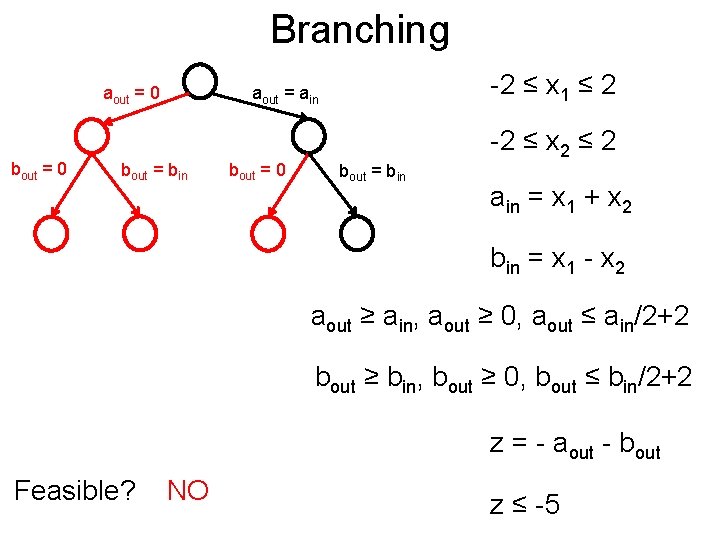
Branching Post aout = 0 bout = bin -2 ≤ x 1 ≤ 2 aout = ain bout = 0 bout = bin -2 ≤ x 2 ≤ 2 ain = x 1 + x 2 bin = x 1 - x 2 aout ≥ ain, aout ≥ 0, aout ≤ ain/2+2 bout ≥ bin, bout ≥ 0, bout ≤ bin/2+2 z = - aout - bout Prune away z ≤ -5

Branching Post aout = 0 bout = 0 -2 ≤ x 1 ≤ 2 aout = ain bout = bin bout = 0 bout = bin -2 ≤ x 2 ≤ 2 ain = x 1 + x 2 bin = x 1 - x 2 aout ≥ ain, aout ≥ 0, aout ≤ ain/2+2 bout ≥ bin, bout ≥ 0, bout ≤ bin/2+2 z = - aout - bout Feasible? NO z ≤ -5

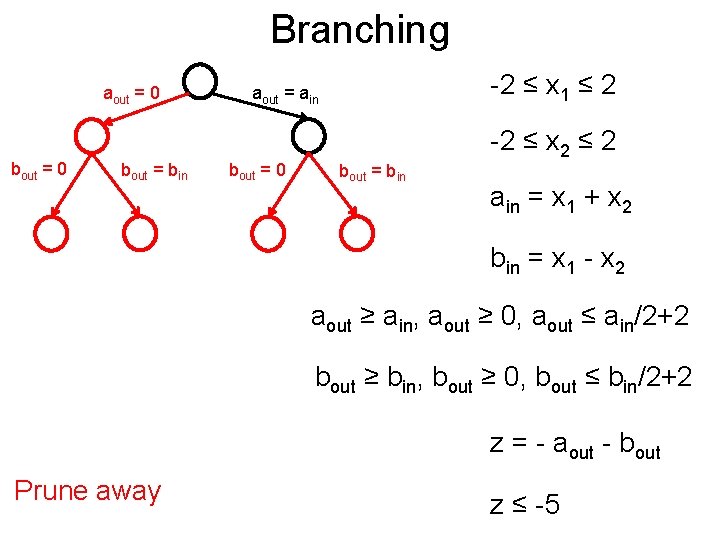
Branching Post aout = 0 bout = bin -2 ≤ x 1 ≤ 2 aout = ain bout = 0 bout = bin -2 ≤ x 2 ≤ 2 ain = x 1 + x 2 bin = x 1 - x 2 aout ≥ ain, aout ≥ 0, aout ≤ ain/2+2 bout ≥ bin, bout ≥ 0, bout ≤ bin/2+2 z = - aout - bout Prune away z ≤ -5

Branching Post aout = 0 bout = bin -2 ≤ x 1 ≤ 2 aout = ain bout = 0 bout = bin -2 ≤ x 2 ≤ 2 ain = x 1 + x 2 bin = x 1 - x 2 aout ≥ ain, aout ≥ 0, aout ≤ ain/2+2 bout ≥ bin, bout ≥ 0, bout ≤ bin/2+2 z = - aout - bout Property must be true z ≤ -5

Outline • Reluplex • Planet • Input Domain Branch-and-Bound • Result Bunel, Turkaslan, Torr, Kohli and Kumar, 2018

Example Post -2 ≤ x 1 ≤ 2 -2 ≤ x 2 ≤ 2 a 1 [-2, 2] x 1 ain = x 1 + x 2 -1 1 z [-2, 2] 1 x 2 -1 -1 b Prove that z > -5 bin = x 1 - x 2 aout = max{ain, 0} bout = max{bin, 0} z = - aout - bout

Bounding Post -2 ≤ x 1 ≤ 2 -2 ≤ x 2 ≤ 2 ain = x 1 + x 2 bin = x 1 - x 2 aout = max{ain, 0} bout = max{bin, 0} z = - aout - bout Relax all non-linearities

Relaxation Post ain ∈ [l, u] aout = max{ain, 0} aout l Replace with convex superset u ain

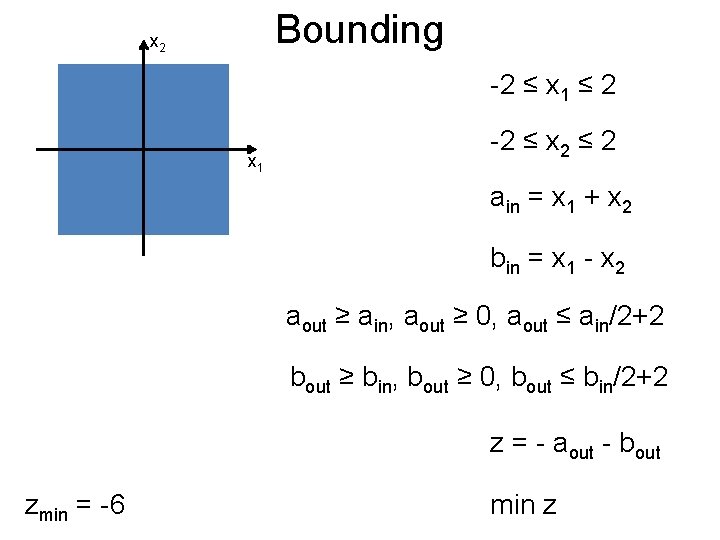
Bounding Post x 2 -2 ≤ x 1 ≤ 2 x 1 -2 ≤ x 2 ≤ 2 ain = x 1 + x 2 bin = x 1 - x 2 aout ≥ ain, aout ≥ 0, aout ≤ ain/2+2 bout ≥ bin, bout ≥ 0, bout ≤ bin/2+2 z = - aout - bout zmin = -6 min z

Bounding Post x 2 -2 ≤ x 1 ≤ 2 x 1 -2 ≤ x 2 ≤ 2 ain = x 1 + x 2 bin = x 1 - x 2 aout ≥ ain, aout ≥ 0, aout ≤ ain/2+2 bout ≥ bin, bout ≥ 0, bout ≤ bin/2+2 z = - aout - bout min z

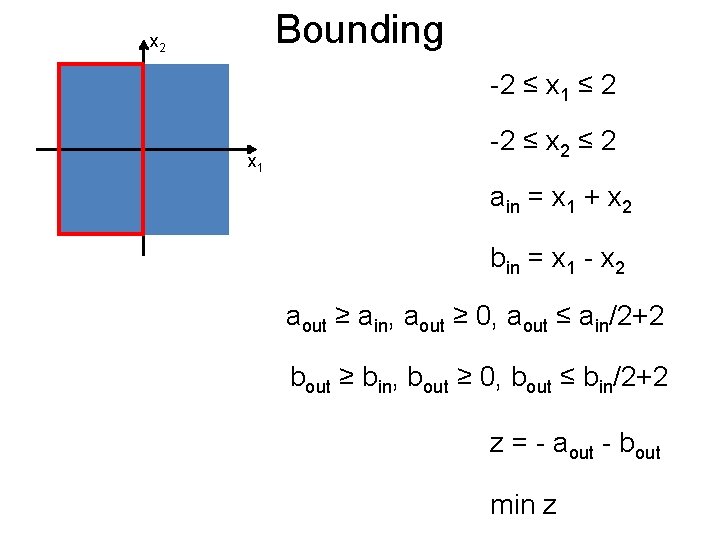
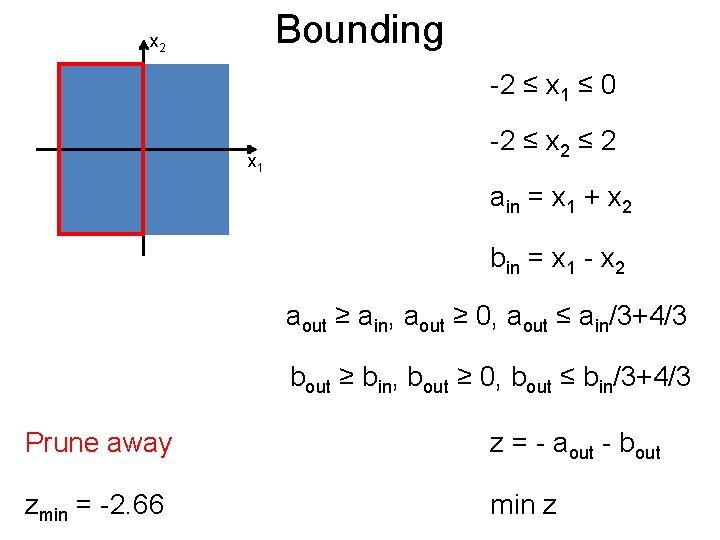
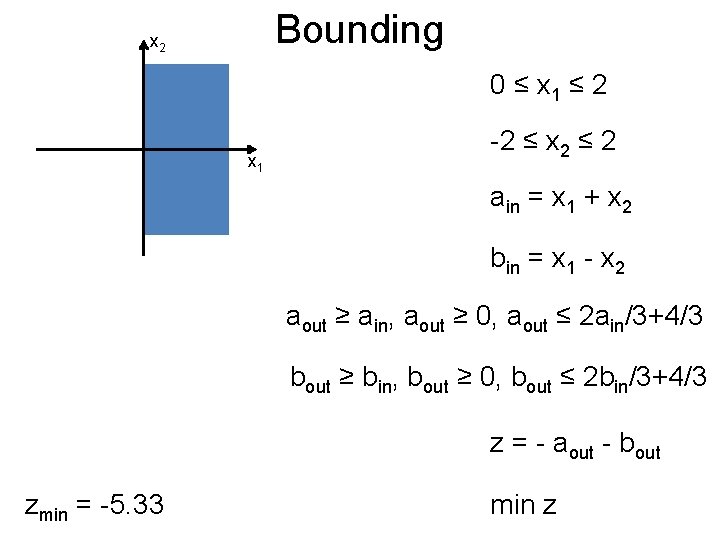
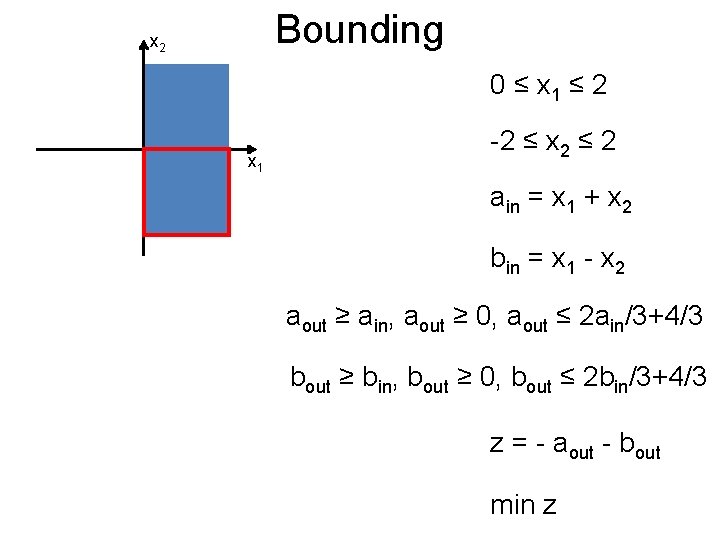
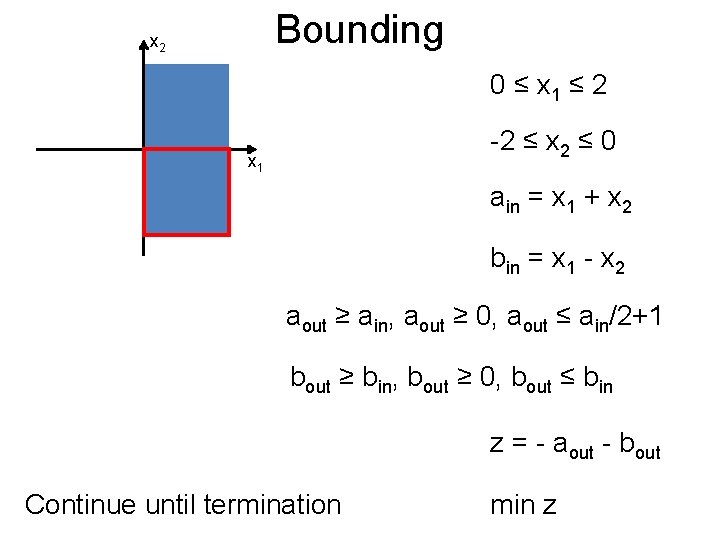
Bounding Post x 2 -2 ≤ x 1 ≤ 0 x 1 -2 ≤ x 2 ≤ 2 ain = x 1 + x 2 bin = x 1 - x 2 aout ≥ ain, aout ≥ 0, aout ≤ ain/3+4/3 bout ≥ bin, bout ≥ 0, bout ≤ bin/3+4/3 Prune away z = - aout - bout zmin = -2. 66 min z

Bounding Post x 2 0 ≤ x 1 ≤ 2 x 1 -2 ≤ x 2 ≤ 2 ain = x 1 + x 2 bin = x 1 - x 2 aout ≥ ain, aout ≥ 0, aout ≤ 2 ain/3+4/3 bout ≥ bin, bout ≥ 0, bout ≤ 2 bin/3+4/3 z = - aout - bout zmin = -5. 33 min z

Bounding Post x 2 0 ≤ x 1 ≤ 2 x 1 -2 ≤ x 2 ≤ 2 ain = x 1 + x 2 bin = x 1 - x 2 aout ≥ ain, aout ≥ 0, aout ≤ 2 ain/3+4/3 bout ≥ bin, bout ≥ 0, bout ≤ 2 bin/3+4/3 z = - aout - bout min z

Bounding Post x 2 0 ≤ x 1 ≤ 2 -2 ≤ x 2 ≤ 0 x 1 ain = x 1 + x 2 bin = x 1 - x 2 aout ≥ ain, aout ≥ 0, aout ≤ ain/2+1 bout ≥ bin, bout ≥ 0, bout ≤ bin z = - aout - bout Continue until termination min z

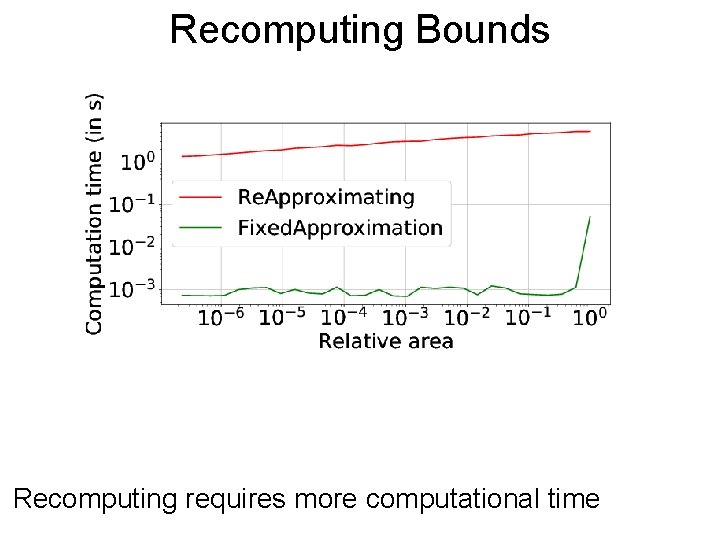
Recomputing Post Bounds Recomputing requires more computational time

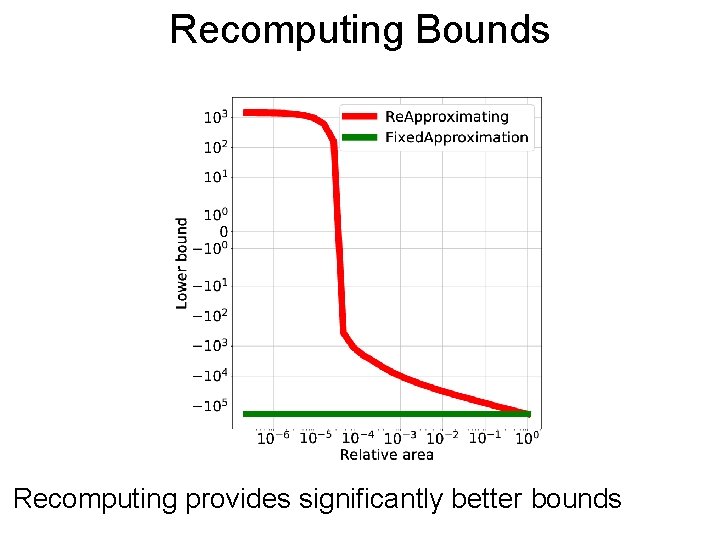
Recomputing Post Bounds Recomputing provides significantly better bounds

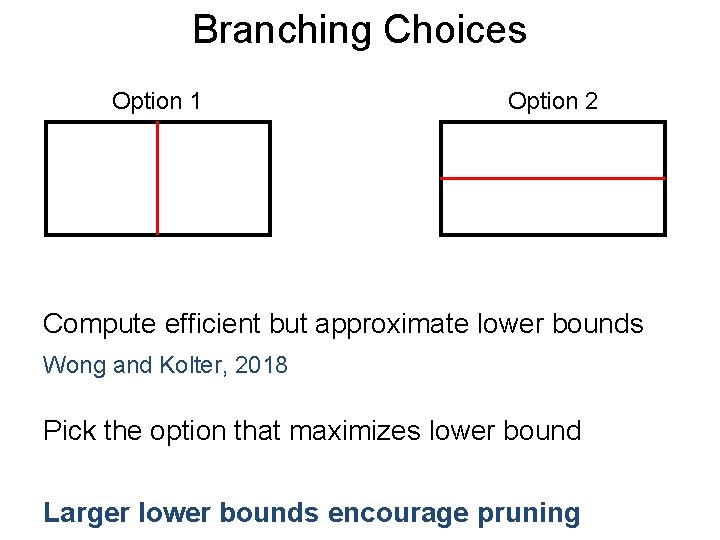
Branching Post. Choices Option 1 Option 2 Compute efficient but approximate lower bounds Wong and Kolter, 2018 Pick the option that maximizes lower bound Larger lower bounds encourage pruning

Outline • Reluplex • Planet • Input Domain Branch-and-Bound • Result

ACASPost Data Set Publicly available data set Katz et al. , 2017 188 properties to verify 5 inputs, 6 hidden layers of 50 units 5 outputs corresponding to aircraft maneuvers

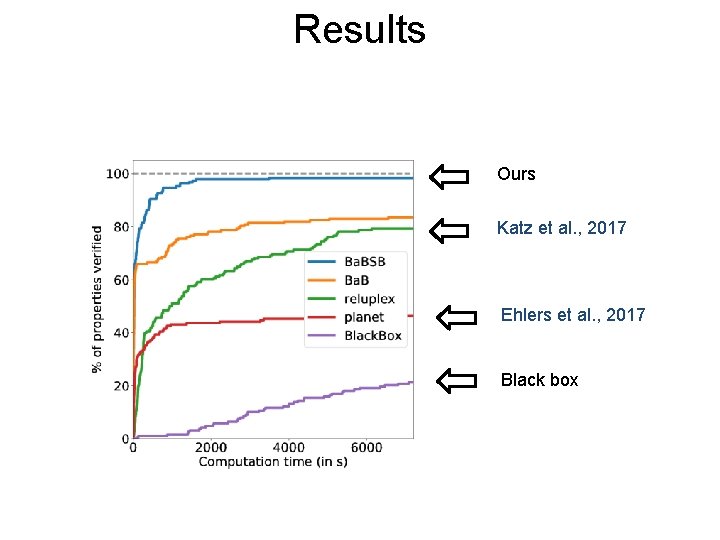
Results Post Black box solvers verify ~20% properties before timeout Cheng et al. , 2017; Tjeng et al. , 2017 Previous branch-and-bound verifies ~40% properties Ehlers 2017; Katz et al. , 2017 Improved algorithm verifies almost all properties Two orders of magnitude speed-up

Results Post Ours Katz et al. , 2017 Ehlers et al. , 2017 Black box

Questions?