Artificial Neural Networks n Artificial Neural Networks are













- Slides: 20

Artificial Neural Networks n Artificial Neural Networks are another technique for supervised machine learning Training Data Test Data k-Nearest Neighbor Decision Tree Logic statements Neural Network Clasification

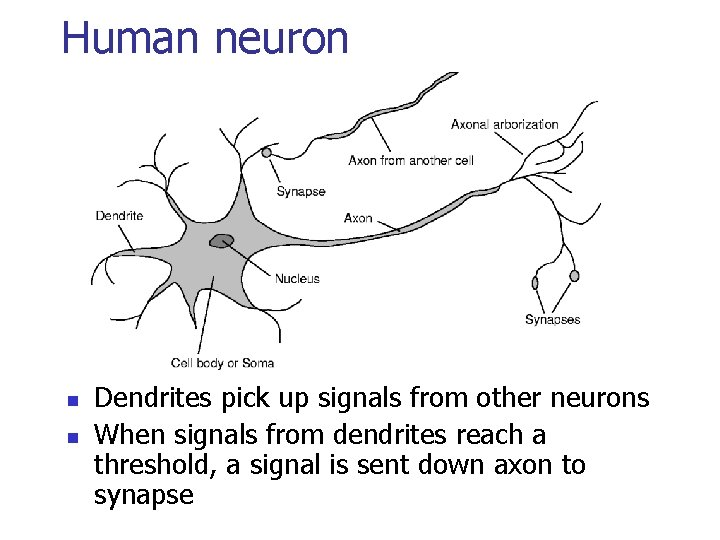
Human neuron n n Dendrites pick up signals from other neurons When signals from dendrites reach a threshold, a signal is sent down axon to synapse

Connection with AI n Most modern AI: n n Implementing neurons in a computer n n “Systems that act rationally” “Systems that think like humans” Why artificial neural networks then? n n “Universal” function fitter Potential for massive parallelism Some amount of fault-tolerance Trainable by inductive learning, like other supervised learning teachniques

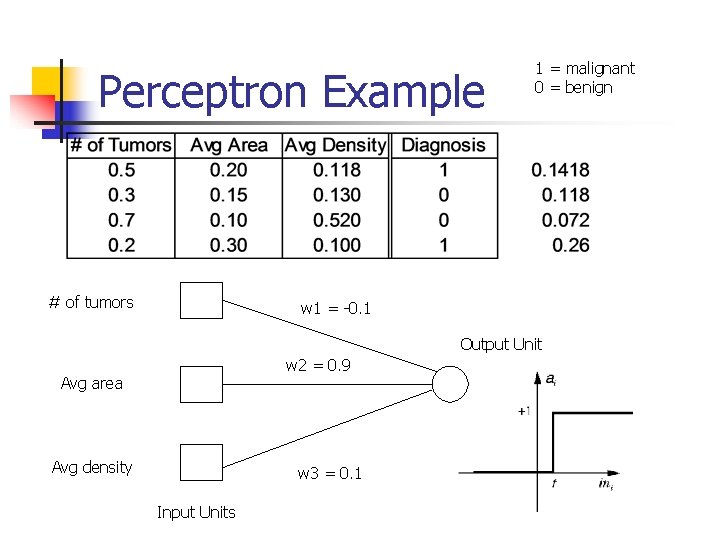
Perceptron Example # of tumors 1 = malignant 0 = benign w 1 = -0. 1 Output Unit w 2 = 0. 9 Avg area Avg density w 3 = 0. 1 Input Units

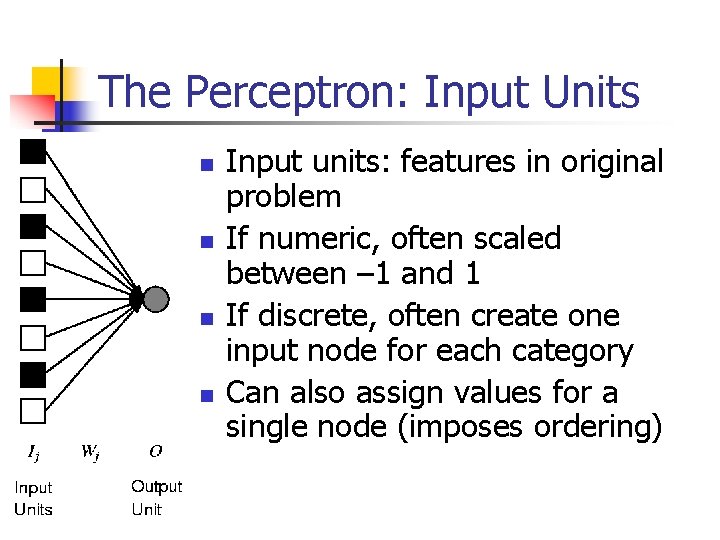
The Perceptron: Input Units n n Input units: features in original problem If numeric, often scaled between – 1 and 1 If discrete, often create one input node for each category Can also assign values for a single node (imposes ordering)

The Perceptron: Weights n n n Weights: Represent importance of each input unit Combined with input units to feed output units The output unit receives as input:

The Perceptron: Output Unit n n The output unit uses an activation function to decide what the correct output is Sample activation function:

Simplifying the threshold n Managing the threshold is cumbersome n Incorporate as a “virtual” weight

How do we compute weights? n Initialize all weights randomly n n Usually between [-0. 5, 0. 5] Put the first point through the network n n Actual Output: Define Error = Correct Output – Actual Output

1 = malignant 0 = benign Perceptron Example # of tumors w 1 = -0. 3 w 0 = 0 Output Unit w 2 = -0. 2 Avg area Avg density w 3 = 0. 4 Input Units Actual Output = 0 Correct Output = 1 Error = 1 – 0 = 1 If input is positive, want weight to be more positive If input is negative, want weight to be more negative

The Perceptron Learning Rule: How do we compute weights? n Put the first point through the network n n n Actual Output: Define Error = Correct Output – Actual Output Update all weights: a = learning rate Repeat with all points, then all points again, and again, until all correct or stopping criterion reached

Can appropriate weights always be found? n ONLY IF data is linearly separable

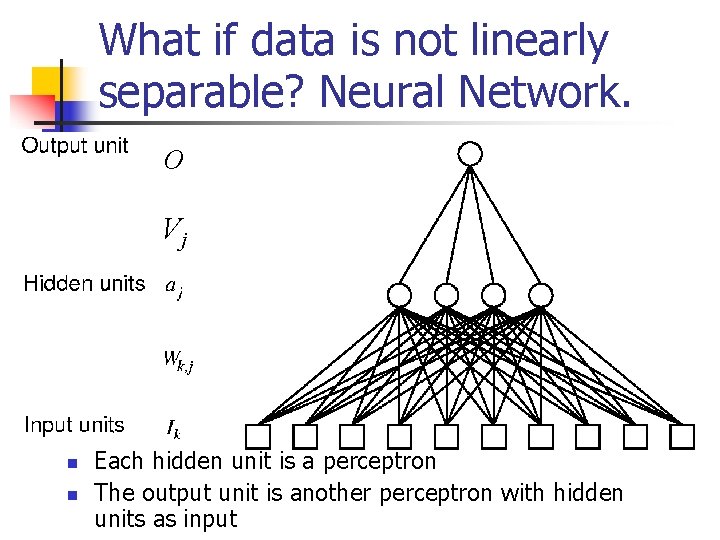
What if data is not linearly separable? Neural Network. O Vj n n Each hidden unit is a perceptron The output unit is another perceptron with hidden units as input

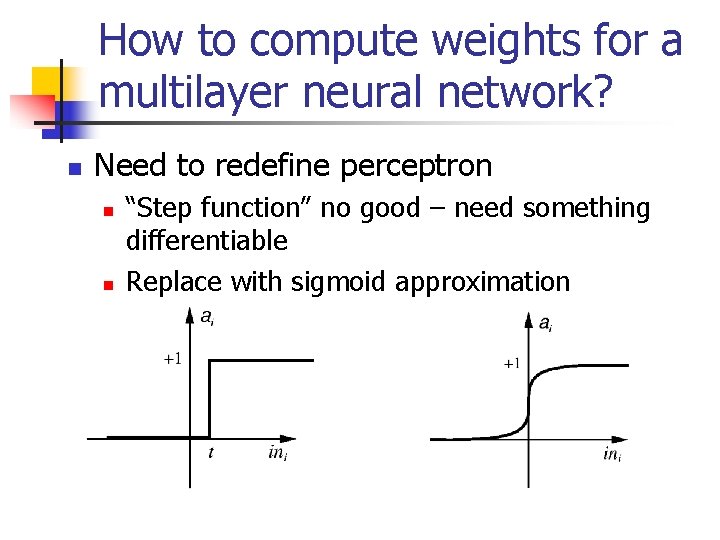
How to compute weights for a multilayer neural network? n Need to redefine perceptron n n “Step function” no good – need something differentiable Replace with sigmoid approximation

Sigmoid function n Good approximation to step function As b infinity, sigmoid step We’ll just take b = 1 for simplicity

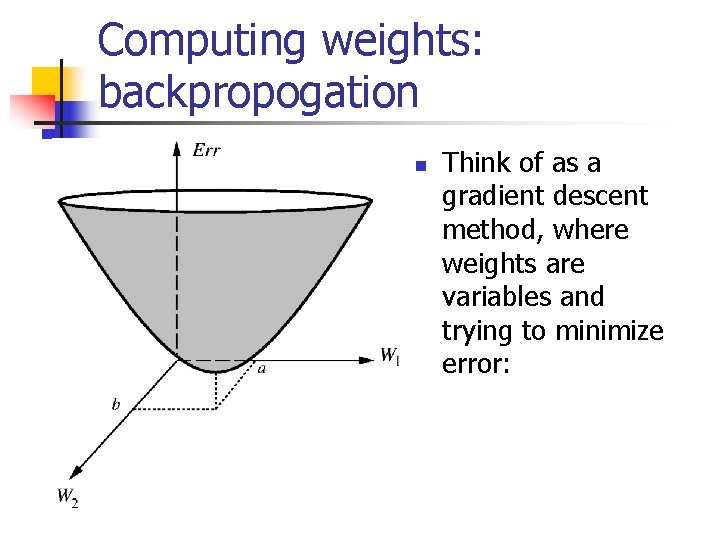
Computing weights: backpropogation n Think of as a gradient descent method, where weights are variables and trying to minimize error:

Minimize squared errors n For all training points, let n n Tp = correct output Op = actual output Want to minimize error Work with one point at a time, and move weights in direction to reduce error the most

Expand (drop the p for simplicity) n Direction of most rapid positive rate of change (gradient) is given by partial derivative Update rule for hidden layer

Simplify as n Input layer backprop is similar, but requires some more chain rule partial derivatives

Neural Networks and machine learning issues n n n Neural networks can represent any training set, if enough hidden units are used How long do they take to train? How much memory? Does backprop find the best set of weights? How to deal with overfitting? How to interpret results?
 Insidan region jh
Insidan region jh Conclusion of artificial neural network
Conclusion of artificial neural network Pengertian artificial neural network
Pengertian artificial neural network Artificial neural network in data mining
Artificial neural network in data mining Neural network terminology
Neural network terminology Fuzzy logic lecture
Fuzzy logic lecture Matlab neural network toolbox pdf
Matlab neural network toolbox pdf Audio super resolution using neural networks
Audio super resolution using neural networks Gated recurrent unit in deep learning
Gated recurrent unit in deep learning Deep forest towards an alternative to deep neural networks
Deep forest towards an alternative to deep neural networks Sparse convolutional neural networks
Sparse convolutional neural networks Mippers
Mippers Audio super resolution using neural networks
Audio super resolution using neural networks Introduction to convolutional neural networks
Introduction to convolutional neural networks Visualizing and understanding convolutional neural networks
Visualizing and understanding convolutional neural networks Neural networks for rf and microwave design
Neural networks for rf and microwave design Convolutional neural networks for visual recognition
Convolutional neural networks for visual recognition Predicting nba games using neural networks
Predicting nba games using neural networks Convolutional neural networks
Convolutional neural networks On the computational efficiency of training neural networks
On the computational efficiency of training neural networks Cnn ppt
Cnn ppt