Modlisation des Effets Cumulatifs des Expositions et des









![Variation over Time of Dose X(t) [Upper graph] & the resulting WCE(u) calculated using Variation over Time of Dose X(t) [Upper graph] & the resulting WCE(u) calculated using](https://slidetodoc.com/presentation_image_h/20e2d14a794b6ca3472d23857190d376/image-14.jpg)

![Flexible spline-based WCE Model [Sylvestre & Abrahamowicz (SIM 2009)] l In our Flexible WCE Flexible spline-based WCE Model [Sylvestre & Abrahamowicz (SIM 2009)] l In our Flexible WCE](https://slidetodoc.com/presentation_image_h/20e2d14a794b6ca3472d23857190d376/image-16.jpg)


![Simulations Results: True w(u-t) (white) vs 100 Constrained Estimates [a=180 days] From Sylvestre and Simulations Results: True w(u-t) (white) vs 100 Constrained Estimates [a=180 days] From Sylvestre and](https://slidetodoc.com/presentation_image_h/20e2d14a794b6ca3472d23857190d376/image-19.jpg)





![SIMULATIONS: Estimates of NON-Linear function [N=600; 300 events] at selected times in the past SIMULATIONS: Estimates of NON-Linear function [N=600; 300 events] at selected times in the past](https://slidetodoc.com/presentation_image_h/20e2d14a794b6ca3472d23857190d376/image-29.jpg)







![Identifiability problems l Because w(u-t) is multiplied by g[X(t)], the 2 functions “share the Identifiability problems l Because w(u-t) is multiplied by g[X(t)], the 2 functions “share the](https://slidetodoc.com/presentation_image_h/20e2d14a794b6ca3472d23857190d376/image-40.jpg)

![Flexible WCE Model [Sylvestre & Abrahamowicz (2009)] l WCE in (2) is then modeled Flexible WCE Model [Sylvestre & Abrahamowicz (2009)] l WCE in (2) is then modeled](https://slidetodoc.com/presentation_image_h/20e2d14a794b6ca3472d23857190d376/image-43.jpg)

![Simulations Results: True w(u-t) (white) vs 100 Un-constrained Estimates [a=180 days] From Sylvestre and Simulations Results: True w(u-t) (white) vs 100 Un-constrained Estimates [a=180 days] From Sylvestre and](https://slidetodoc.com/presentation_image_h/20e2d14a794b6ca3472d23857190d376/image-45.jpg)



![Estimates of w( ) [N=600; ~300 events] Estimates of w( ) [N=600; ~300 events]](https://slidetodoc.com/presentation_image_h/20e2d14a794b6ca3472d23857190d376/image-49.jpg)




![Cubic Regression Spline Basis Weight function in (2) [on slide 16] is estimated using Cubic Regression Spline Basis Weight function in (2) [on slide 16] is estimated using](https://slidetodoc.com/presentation_image_h/20e2d14a794b6ca3472d23857190d376/image-54.jpg)

- Slides: 57

Modélisation des Effets Cumulatifs des Expositions et des Facteurs Pronostiques Michal Abrahamowicz, Ph. D* James Mc. Gill Professor Department of Epidemiology & Biostatistics Mc. Gill University, Montreal, Quebec, CANADA & Marie-Pierre Sylvestre, Ph. D Professeur Adjoint, Universite de Montreal, Quebec, CANADA 1

Outline 1. 2. 3. 4. 5. 6. 7. 8. Objectives Challenges in modeling the effects of Time. Varying exposures/treatments/prognostic factors Flexible estimation of Cumulative Effects Evaluation via Simulations Pharmaco-epidemiologic Application Inclusion of Non-linear Effects Application: Impact of Past SBP on CVD risks Conclusions

Objectives l l To emphasize the Importance of accounting for Cumulative Effects of Past Exposures/Prognostic Factors To introduce New Flexible Methods for Modeling Cumulative Effects To Evaluate proposed methods in Simulations To Illustrate Real-Life Applications in Etiologic (Pharmaco-epidemiologic) and Prognostic Studies

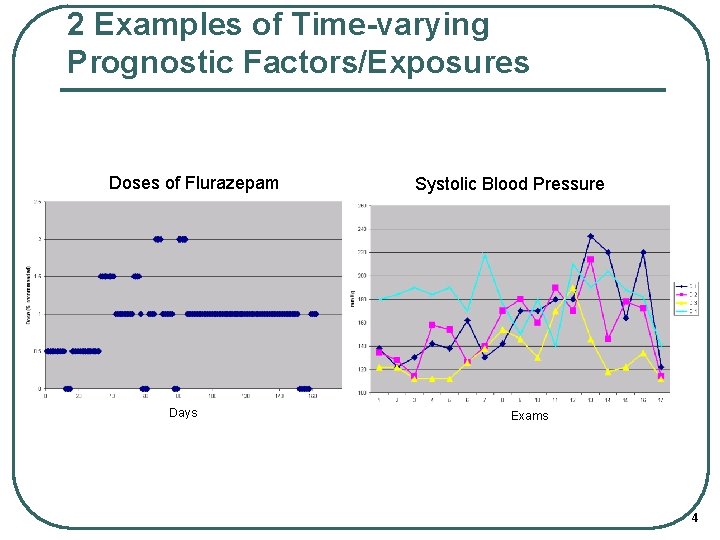
2 Examples of Time-varying Prognostic Factors/Exposures Doses of Flurazepam Days Systolic Blood Pressure Exams 4

Main Challenge in Modeling Effects of Time-Varying Exposures/Risk Factors l How to relate the Entire History of Past Values of the Exposure with Current Risk of the Outcome ?

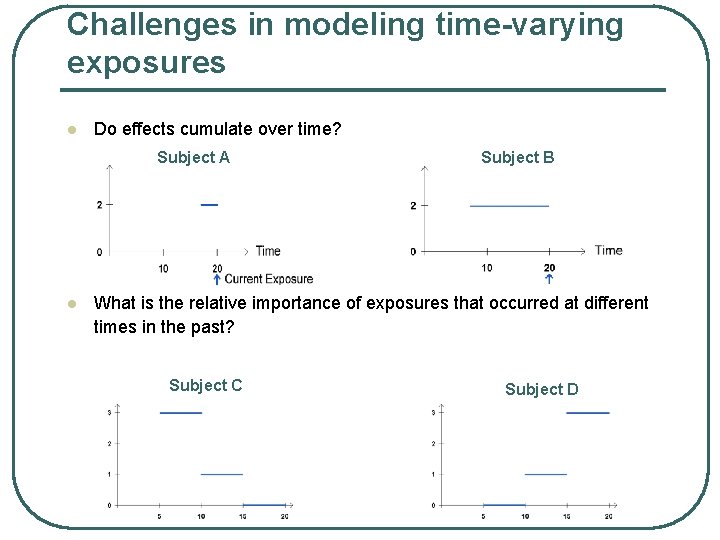
Challenges in modeling time-varying exposures l Do effects cumulate over time? Subject A l Subject B What is the relative importance of exposures that occurred at different times in the past? Subject C Subject D

Examples of Cumulative Effects l l l Adverse Effects of Psychotropic Medications: Short-term Cumulative Effects may occur until the drug is entirely eliminated from the Plasma (but Recent doses have the highest impact) Impact of Smoking on Lung Cancer Risk: an example of Long-Term Cumulative Effect (Impact of Past Smoking cumulates over Lifetime but there is a

Conventional Models for Time-Varying Prognostic Factors l Different models are used to relate the hazard at current time u with a time-varying exposure: i. ii. iii. iv. v. Current value (“dose”): X(u) Total Past Dose (=un-weighted cumulative dose) Total Duration of Past Exposure Any Exposure e. g. in the Last Month Mean Dose e. g. in the Last Month

(Some) Limitations of Conventional Models l All “conventional models” impose strong A Priori assumptions about the Relative Importance of Past Doses (X(t), t<u) for determining Current Risk at time u. e. g. : i. ii. the Current Dose model assumes that ONLY the Current Dose X(u) does matter In contrast, the Total Dose model assumes that ALL Past Doses have Equal Impact on the current risk,

Weighted Cumulative Exposure (WCE) model l All conventional models (i)-(iii) are special cases of a much more General Model, based on the Concept of: recency-Weighted Cumulative Exposure (WCE), where the Cumulative Effect is modeled as a Weighted Sum ** of all Past Doses,

Recency-weighted cumulative exposure (WCE) Abrahamowicz et al. (2006), Breslow et al. (1983), Hauptmann et al. (2000), Thomas (1988), Vacek (1997) (1) where: u= current time (when Risk is being assessed) WCE(u)= Weighted Cumulative Effect of the Past Exposures on Risk at time u X(t)= exposure intensity (dose) at time t(t≤u) u-t= time elapsed since exposure X(t) w(u-t)= Weight (Relative Importance) assigned to exposure X(t) as a function of Time-since-Exposure (u-t) 11

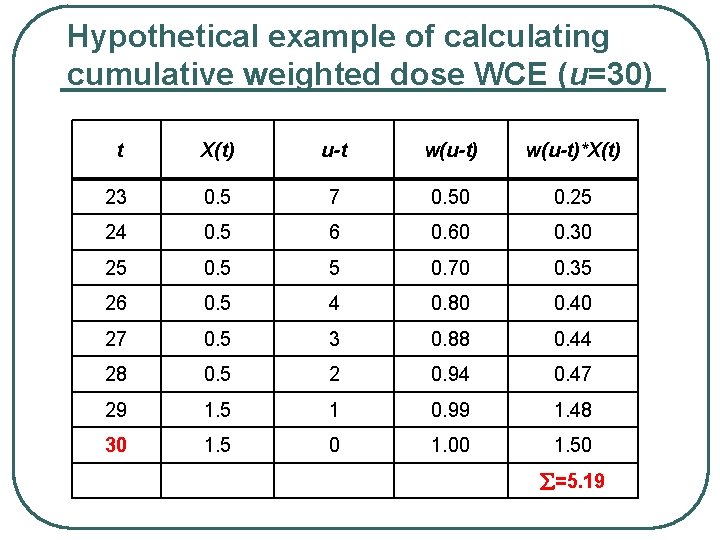
Hypothetical example of calculating cumulative weighted dose WCE (u=30) t X(t) u-t w(u-t)*X(t) 23 0. 5 7 0. 50 0. 25 24 0. 5 6 0. 60 0. 30 25 0. 5 5 0. 70 0. 35 26 0. 5 4 0. 80 0. 40 27 0. 5 3 0. 88 0. 44 28 0. 5 2 0. 94 0. 47 29 1. 5 1 0. 99 1. 48 30 1. 5 0 1. 00 1. 50 =5. 19

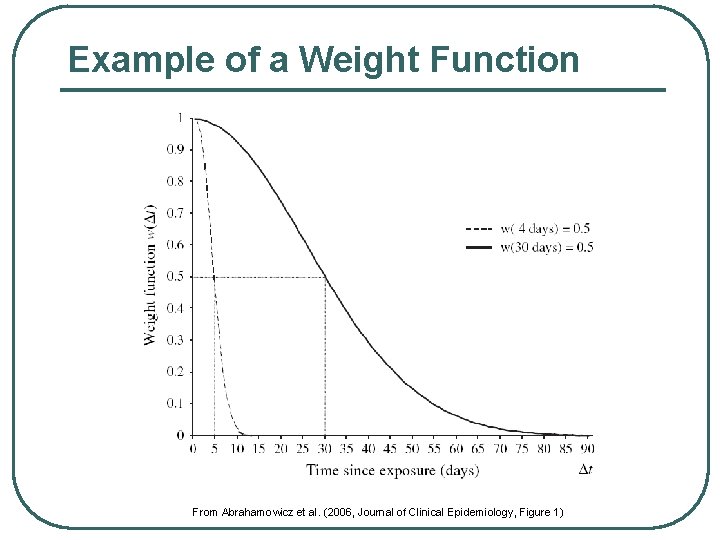
Example of a Weight Function From Abrahamowicz et al. (2006, Journal of Clinical Epidemiology, Figure 1)
![Variation over Time of Dose Xt Upper graph the resulting WCEu calculated using Variation over Time of Dose X(t) [Upper graph] & the resulting WCE(u) calculated using](https://slidetodoc.com/presentation_image_h/20e2d14a794b6ca3472d23857190d376/image-14.jpg)
Variation over Time of Dose X(t) [Upper graph] & the resulting WCE(u) calculated using w(u-t) on slide 12 [Lower graph]) From Abrahamowicz et al. (2006, Journal of Clinical Epidemiology, Figure 2)

Need for Flexible Modeling of the Weight Function l In most real-life prognostic studies, there is little A priori knowledge about the (i) Exact Shape, and (ii) the Exact Values of the Weight Function l Therefore, it would be Advantageous to Estimate the Weight Function Directly from the Empirical Data l To this end, we need Flexible Assumptions-free methods such as Splines
![Flexible splinebased WCE Model Sylvestre Abrahamowicz SIM 2009 l In our Flexible WCE Flexible spline-based WCE Model [Sylvestre & Abrahamowicz (SIM 2009)] l In our Flexible WCE](https://slidetodoc.com/presentation_image_h/20e2d14a794b6ca3472d23857190d376/image-16.jpg)
Flexible spline-based WCE Model [Sylvestre & Abrahamowicz (SIM 2009)] l In our Flexible WCE model, the Weight function is estimated by Cubic Splines: (2) where Bj, j=1, …, m, represent the m functions in the Cubic Spline basis, and j represent the estimable coefficients of the linear combination of the basis splines WCE in (2) is then modeled as a

Examples of Cubic Regression Splines (with 3 Interior Knots) The m functions Bj of the cubic spline basis B 1 B 2 B 3 B 4 Regression spline u-t = (0. 6, 0. 9, 0. 4, 0. 2) = (0. 5, 0. 1, 0. 2, 0. 4, 0. 2, 0. 5) Interior knots

Inference about the Estimated Weight Function ŵ( ) l Quasi-parametric LRT tests* of: i. ii. l H 0 = No Association between X(t) and risk: w(u-t)=0 for 0<t<u (df=k+4) H 0 = Equal Weighting of All past values: w(u-t)=V for 0<t<u (df=k+3) Bootstrap-based pointwise confidence bands around the estimated Weight function
![Simulations Results True wut white vs 100 Constrained Estimates a180 days From Sylvestre and Simulations Results: True w(u-t) (white) vs 100 Constrained Estimates [a=180 days] From Sylvestre and](https://slidetodoc.com/presentation_image_h/20e2d14a794b6ca3472d23857190d376/image-19.jpg)
Simulations Results: True w(u-t) (white) vs 100 Constrained Estimates [a=180 days] From Sylvestre and Abrahamowicz (2009, Statistics in Medicine, Figure 2)

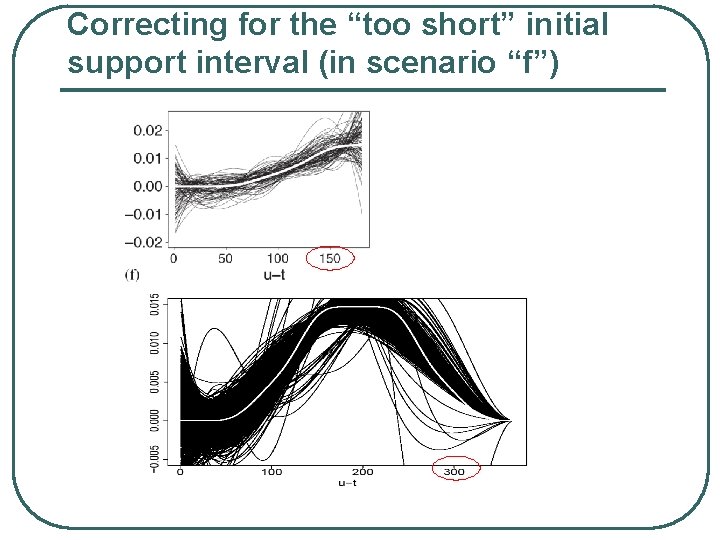
Simulation Results: Goodness of Fit of Alternative Models l In scenarios (a) – (d) [where the True weight function decayed to 0], the Constrained models had the best fit (lowest BIC) in > 90% of the simulated samples l In scenario (e) the (conventional) UN-weighted Total Cumulative Dose (corresponding to the “true” model) had the lowest BIC in in > 90% of the simulated samples (this Eliminated concerns about the Over-fit bias of the weighted estimates) l In scenario (f) the Un-constrained model fitted better than the constrained estimate and the former suggested that doses taken > 180 days ago are still relevant

Correcting for the “too short” initial support interval (in scenario “f”)

APPLICATION: Flurazepam (a Psychotropic drug) use vs Fall-related Injuries in Elderly l l l l Data from Dr. Robyn Tamblyn from Mc. Gill University Prospective study based on Administrative Health Data (Prescription Claims database) from the Canadian province of Quebec Cohort of N=4, 666 elderly New Users of Flurazepam (started use in 1990 -1994) T 0 = Jan. 1, 1990 (Delayed Entry at the time of the 1 st Flurazepam prescription) Event = Fall-related Injury [252 events] Available Data for Each Prescription: (i) Duration & (ii) Daily Standardized Dose 3 “time windows”: a = 60, 90 & 180 days

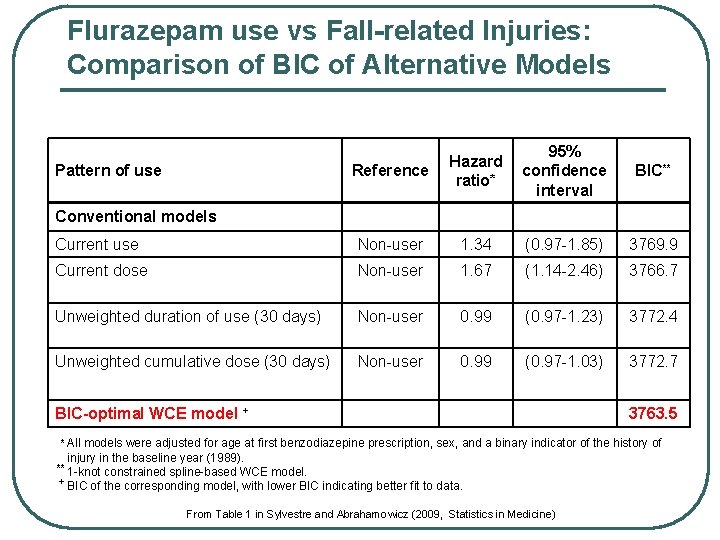
Flurazepam use vs Fall-related Injuries: Comparison of BIC of Alternative Models Reference Hazard ratio* 95% confidence interval BIC** Current use Non-user 1. 34 (0. 97 -1. 85) 3769. 9 Current dose Non-user 1. 67 (1. 14 -2. 46) 3766. 7 Unweighted duration of use (30 days) Non-user 0. 99 (0. 97 -1. 23) 3772. 4 Unweighted cumulative dose (30 days) Non-user 0. 99 (0. 97 -1. 03) 3772. 7 Pattern of use Conventional models BIC-optimal WCE model + 3763. 5 * All models were adjusted for age at first benzodiazepine prescription, sex, and a binary indicator of the history of injury in the baseline year (1989). ** 1 -knot constrained spline-based WCE model. + BIC of the corresponding model, with lower BIC indicating better fit to data. From Table 1 in Sylvestre and Abrahamowicz (2009, Statistics in Medicine)

Flurazepam vs Falls: Constrained WEIGHT function with a=60 (Cubic Spline; 1 knot) From Sylvestre and Abrahamowicz (2009, Statistics in Medicine, Figure 3)

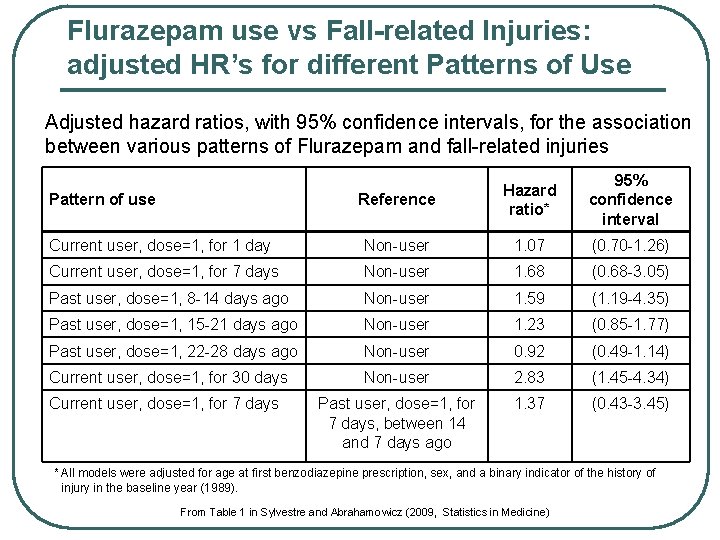
Flurazepam use vs Fall-related Injuries: adjusted HR’s for different Patterns of Use Adjusted hazard ratios, with 95% confidence intervals, for the association between various patterns of Flurazepam and fall-related injuries Reference Hazard ratio* 95% confidence interval Current user, dose=1, for 1 day Non-user 1. 07 (0. 70 -1. 26) Current user, dose=1, for 7 days Non-user 1. 68 (0. 68 -3. 05) Past user, dose=1, 8 -14 days ago Non-user 1. 59 (1. 19 -4. 35) Past user, dose=1, 15 -21 days ago Non-user 1. 23 (0. 85 -1. 77) Past user, dose=1, 22 -28 days ago Non-user 0. 92 (0. 49 -1. 14) Current user, dose=1, for 30 days Non-user 2. 83 (1. 45 -4. 34) Current user, dose=1, for 7 days Past user, dose=1, for 7 days, between 14 and 7 days ago 1. 37 (0. 43 -3. 45) Pattern of use * All models were adjusted for age at first benzodiazepine prescription, sex, and a binary indicator of the history of injury in the baseline year (1989). From Table 1 in Sylvestre and Abrahamowicz (2009, Statistics in Medicine)

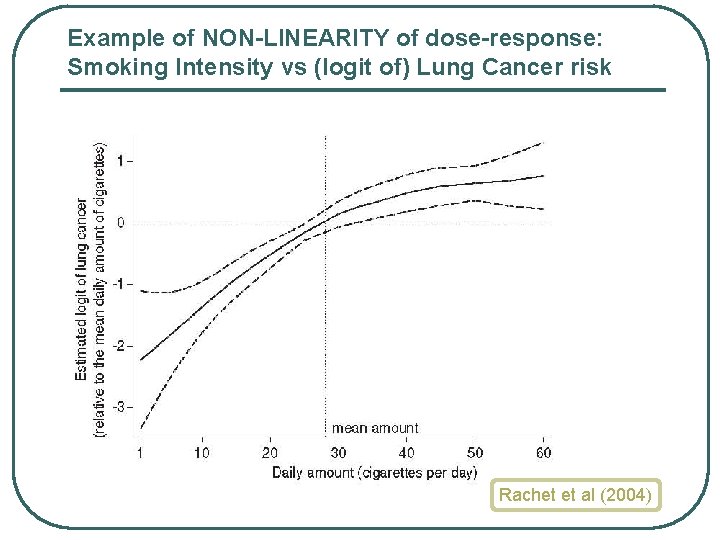
Another Challenge: unknown Dose. Response function for continuous X(t) l l “Classic” WCE model (1), assumes Linear relationship between “dose” X(t) and risk (e. g. , Logit or Log hazard) Yet, many continuous exposures have Non. Linear effects on risk! [e. g. Abrahamowicz et al, AJE 1997] Ø Need to Extend the WCE models to incorporate Flexible Modeling of the possibly Non-linear effects of Continuous Time-Varying Prognostic Factors

Example of NON-LINEARITY of dose-response: Smoking Intensity vs (logit of) Lung Cancer risk Rachet et al (2004)

EXTENSION of our flexible WCE model to Joint Estimation of w( ) and g( ) in Time-to-Event analyses (7) l Model w( ) and g( ) with Cubic regression splines 1 or 2 equidistant interior knots 2 interior knots at tertiles of overall distribution of X[t] 28
![SIMULATIONS Estimates of NONLinear function N600 300 events at selected times in the past SIMULATIONS: Estimates of NON-Linear function [N=600; 300 events] at selected times in the past](https://slidetodoc.com/presentation_image_h/20e2d14a794b6ca3472d23857190d376/image-29.jpg)
SIMULATIONS: Estimates of NON-Linear function [N=600; 300 events] at selected times in the past

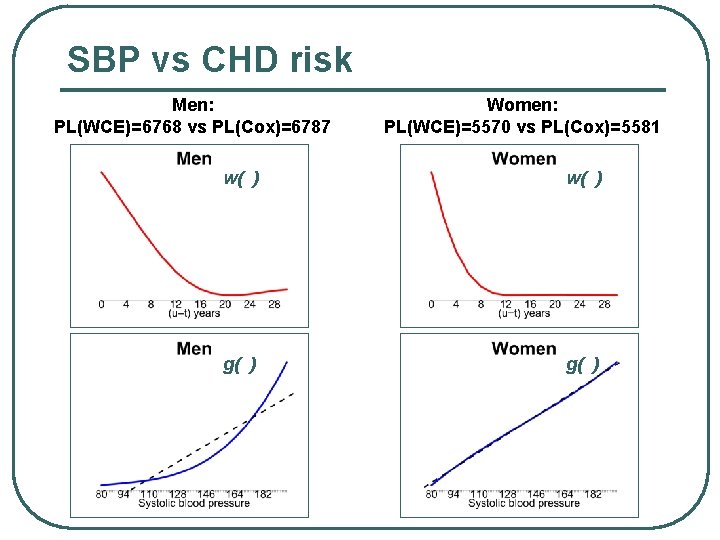
APPLICATION: assessing Relative importance of Past SBP values for CHD risk l l l l Data Source = Framingham Heart Study 30 years of Follow-up with 16 bi-annual exams (SBP and other risk factor measures) Time 0 = 1 st exam Event = 1 st Coronary Heart Disease (CHD) event (mortality/morbidity) 2603 women (762 CHD events) 2128 men (995 CHD events) Adjustment for: current age, serum

SBP vs CHD risk Men: PL(WCE)=6768 vs PL(Cox)=6787 Women: PL(WCE)=5570 vs PL(Cox)=5581 w( ) g( )

Some Limitations of Our Methods l l l Our methods require frequent measurements of the prognostic factor X(t) [≥ 15 observations during the follow-up] The method performs well in Large Databases (> 300 events) The current methods do not handle timevarying mediating/confounding variables (need to extend to Marginal Structural

Conclusions l Flexible Weighted Cumulative Exposure (WCE) model offers New Insights about : 1) Relative Importance of values of Exposures and Risk Factor observed at different times in the Past and their Cumulative Effects on the Current Risk 2) Non-Linear Exposure-Risk relations for continuous variables 33

Conclusions l The flexible WCE model fits data from many Longitudinal Studies better than conventional models and may be useful in All Studies with Repeated-over-Time Measures of Treatments, Exposures, Risk factors or Prognostic factors 34

References l Abrahamowicz M, Bartlett G, Tamblyn R, du Berger R. Modeling cumulative dose and exposure duration provided insights regarding the associations between benzodiazepines and injuries. Journal of Clinical Epidemiology. 2006; 59(4): 393 -403. l Abrahamowicz M, du Berger R, Grover SA. Flexible modeling of the effects of serum cholesterol on coronary heart disease mortality. American Journal of Epidemiology 1997; 145(8): 714 -729. l Abrahamowicz M, Mac. Kenzie T, Esdaile JM. Time-dependent hazard ratio: modeling and hypothesis testing with application in lupus nephritis. Journal of the American Statistical Association. 1996; 91(436): 1432 -39. l Breslow NE, Lubin JH, Marek P, Langholz B. Multiplicative models and cohort analysis. Journal of the American Statistical Society 1983; 78(381): 1– 12. l Hauptmann M, Wellmann J, Lubin JH, Rosenberg PS, Kreienbrock L. Analysis of exposure-time-response relationships using a spline weight function. Biometrics. 2000; 56(4): 1105 -8. l Mac. Kenzie T, Abrahamowicz M. Marginal and hazard ratio specific random data generation: applications to semiparametric bootstrapping. Statistics and Computing. 2002; 12(3): 245 -352. l Mahmud M, Abrahamowicz M, Leffondré K, Chaubey YP. Selecting the optimal transformation of a continuous covariate in Cox’s regression: Implications for hypothesis testing. Communication in Statistics 2006; 35(1): 27 -45. l Rachet B, Siemiatycki J, Abrahamowicz M, Leffondré K. A flexible modeling approach to estimating the component effects of smoking behavior on lung cancer. Journal of Clinical Epidemiology 2004; 57(10): 1076 -1085. l Sylvestre MP, Abrahamowicz M. Comparisons of algorithms to generate event times conditional on time-dependent covariates. Statistics in Medicine. 2008; 27(14): 2618 -34. l Sylvestre MP, Abrahamowicz M. Flexible modeling of the cumulative effects of time-dependent exposures on the hazard. Statistics in Medicine. 2009; 28(27): 3437 -53. l Thomas DC. Models for exposure-time-response relationships with applications to cancer epidemiology. Annual Reviews of Public Health 1988; 9: 451 -82. l Vacek PM. Assessing the effect of intensity when exposure varies over time. Statistics in Medicine. 1997; 16(5): 505 -13.

MERCI ! Michal. Abrahamowicz@mcgill. ca

Additional material 37

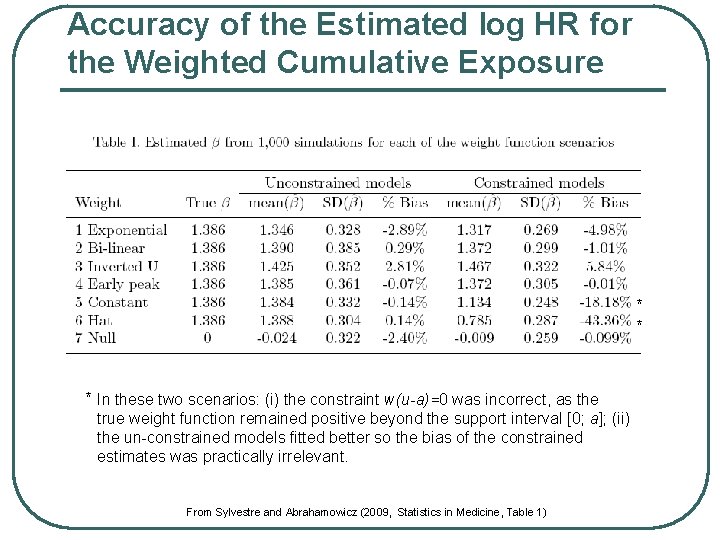
Accuracy of the Estimated log HR for the Weighted Cumulative Exposure * * * In these two scenarios: (i) the constraint w(u-a)=0 was incorrect, as the true weight function remained positive beyond the support interval [0; a]; (ii) the un-constrained models fitted better so the bias of the constrained estimates was practically irrelevant. From Sylvestre and Abrahamowicz (2009, Statistics in Medicine, Table 1)

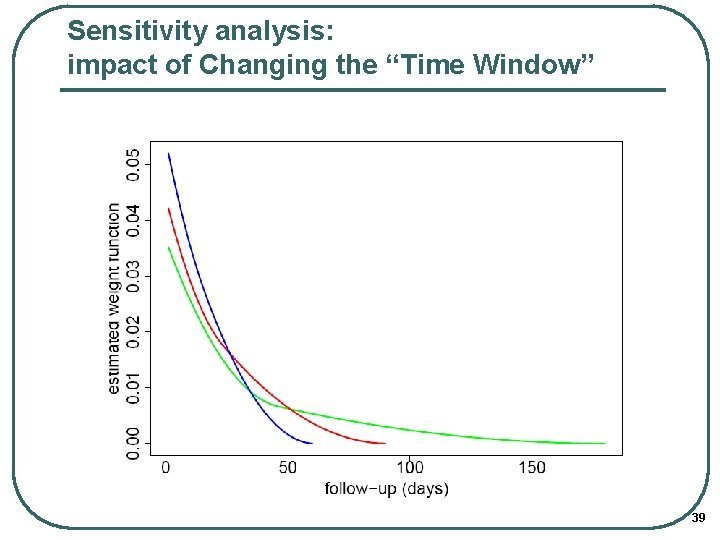
Sensitivity analysis: impact of Changing the “Time Window” 39
![Identifiability problems l Because wut is multiplied by gXt the 2 functions share the Identifiability problems l Because w(u-t) is multiplied by g[X(t)], the 2 functions “share the](https://slidetodoc.com/presentation_image_h/20e2d14a794b6ca3472d23857190d376/image-40.jpg)
Identifiability problems l Because w(u-t) is multiplied by g[X(t)], the 2 functions “share the scale” for r ≠ 0: which implies: i. Identifiability problems [Abrahamowicz & Mac. Kenzie (2007)] ii. Non-linearity of model (7) in its parameters 40

2 -step iterative Alternating Conditional Estimation (ACE) (maximum Partial Likelihood (PL)) l We propose an ACE algorithm that iterates through 2 alternating steps: Estimate w( ) given previous estimate of ĝ( ) 2) Estimate g( ) given previous estimate of ŵ( ) 1) l l l We continue Iterations (through steps 1 & 2) until “Convergence” (ΔPL<0. 01) At step 1) of the 1 st iteration g( ) = αX(t) [Linear] At step 1) of each iteration ŵ( ) is standardized: 41

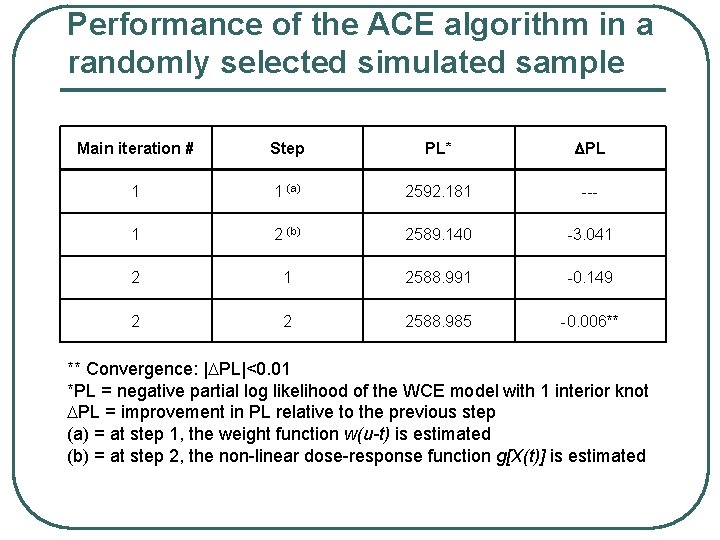
Performance of the ACE algorithm in a randomly selected simulated sample Main iteration # Step PL* PL 1 1 (a) 2592. 181 --- 1 2 (b) 2589. 140 -3. 041 2 1 2588. 991 -0. 149 2 2 2588. 985 -0. 006** ** Convergence: | PL|<0. 01 *PL = negative partial log likelihood of the WCE model with 1 interior knot PL = improvement in PL relative to the previous step (a) = at step 1, the weight function w(u-t) is estimated (b) = at step 2, the non-linear dose-response function g[X(t)] is estimated
![Flexible WCE Model Sylvestre Abrahamowicz 2009 l WCE in 2 is then modeled Flexible WCE Model [Sylvestre & Abrahamowicz (2009)] l WCE in (2) is then modeled](https://slidetodoc.com/presentation_image_h/20e2d14a794b6ca3472d23857190d376/image-43.jpg)
Flexible WCE Model [Sylvestre & Abrahamowicz (2009)] l WCE in (2) is then modeled as a Time-Dependent Covariate in Cox’s model: (3) where: h 0(u) is the baseline hazard, X(u)={X(t), 0≤t≤u} represents the time-vector of the past exposures, Zs(u), s=1, …, q, are the values of the fixed-in-time or time-dependent covariates relevant for time u

Use of Artificial Time-Dependent covariates permits implementation with standard software l To estimate w( ), at step 1 of ACE, construct artificial timedependent covariates: l and fit the following Cox’s model: 44
![Simulations Results True wut white vs 100 Unconstrained Estimates a180 days From Sylvestre and Simulations Results: True w(u-t) (white) vs 100 Un-constrained Estimates [a=180 days] From Sylvestre and](https://slidetodoc.com/presentation_image_h/20e2d14a794b6ca3472d23857190d376/image-45.jpg)
Simulations Results: True w(u-t) (white) vs 100 Un-constrained Estimates [a=180 days] From Sylvestre and Abrahamowicz (2009, Statistics in Medicine, Figure 1)

Simulations Design l l l l Hypothetical Pharmaco-epi study of the Adverse Effects of a drug Cohort of N=500 new drug users t 0 = time of 1 st prescription Follow-up duration up to 1 year Random right censoring (about 50%) 6 simulated scenarios, each with a different ‘true’ weight function Time-varying Patterns of Drug Use/Dose X(t): Øsubjects repeatedly stop and re-start drug use Øboth Inter- & Intra-subject Variation in the length of consecutive Periods of use/non-use & in the Dose Ødose constant within each period of use but varied from one period to another

Use of Artificial Time-Dependent covariates permits implementation with standard software l To estimate g( ), at step 2 of ACE, calculate: l and fit the following Cox’s model: 47

Simulations l i. The Design and Methods of Simulations were Similar to slides 24 -25, Except: ii. “dose” X(t) was generated from a Continuous Distribution U(0, 3); X(t) was assumed to have different Non-linear relationships with the logarithm of the hazard.
![Estimates of w N600 300 events Estimates of w( ) [N=600; ~300 events]](https://slidetodoc.com/presentation_image_h/20e2d14a794b6ca3472d23857190d376/image-49.jpg)
Estimates of w( ) [N=600; ~300 events]

Generation of Event Times Conditional on the WCE via novel ‘Permutational Algorithm’ A. B. C. Generate Individual exposure vectors xs[t], s=1, …, N Generate Observed Event/Censoring Times: 1) 2) • Marginal distribution of Event times Ti ~ U[1, 365] days, i=1, …, N Marginal distribution of Censoring times Ci ~ U[1, 365] days Observed times ti* = min(Ti, Ci) MATCH Exposure Vectors (step A) with Observed Times (step B) via Permutational algorithm [Mac. Kenzie and Abrahamowicz (2002); Sylvestre and Abrahamowicz (2008)] 1) If ti* = event, assign ti* to one of the xs[t] at risk by sampling xs[t] with probability proportional to hazard at ti*: 2) If ti* = censored time, assign ti* to one of the xs[t] at risk by simple random sampling 50

Constrained WCE Model l l In many applications, it may be A Priori evident that the Weight Function w(u-t) should asymptotically decay to 0 at the either end of the support interval [0; a] This can be easily achieved by Constraining the WCE model: Ø 1=0 & 2=0 ensures, respectively, that w(0)=0 & w’(0)=0 so that Current Value X(u) has No Impact on Current Risk at u (e. g. , Current Smoking is Irrelevant for Current Cancer Risk) Ø (k+4)=0 & (k+3)=0 ensures that w(a)=0 & w’(a)=0 so that the Value of X(u-a) has No Impact on the Current Risk (e. g. , Drug Use a days/weeks ago is Irrelevant for Current Risk of Adverse 51

Model Selection l l We fit models with k=1, 2 or 3 ‘interior knots’ (Uniformly Distributed within [0; a] support interval) (in addition, 4 ‘exterior knots’ are placed at both u=0 and u=a) The resulting Cubic Spline has, respectively, 5, 6 or 7 functional segments, i. e. model (6) [slide 21] requires estimating k+4 = 5 -7 coefficients j In some applications, the users may also want to consider Sensitivity Analyses with respect to a (= the Upper Limit of the Support Interval [0; a]) * BIC is used to select the Best-fitting of the Alternative Spline Models (with Different k and/or a) 52

ESTIMATION of the Flexible WCE Model through Artificial Time-varying Covariates From (1), (2) & (3), the effect of WCE is modeled as: where BOTH β & j need to be estimated. To Avoid Identifiability Problems, we define: (4) & construct Artificial Time-varying Covariates: (5) for j=1, …, m 53
![Cubic Regression Spline Basis Weight function in 2 on slide 16 is estimated using Cubic Regression Spline Basis Weight function in (2) [on slide 16] is estimated using](https://slidetodoc.com/presentation_image_h/20e2d14a794b6ca3472d23857190d376/image-54.jpg)
Cubic Regression Spline Basis Weight function in (2) [on slide 16] is estimated using Cubic** Regression Splines with Fixed Knots (= points where consecutive Cubic Polynomials join each other) l Spline Basis is defined over a Limited Support Interval [0; a] where: a = (user-specified) maximum length of the ‘etiologically relevant exposure time window’ [past values of X(t) at t<u-a are a priori considered irrelevant for the risk at time u and, thus, are assigned the weight=0] l ** Cubic splines ensure that w(u-t) and its 1 st & 2 nd Derivatives are Continuous 54

ESTIMATION of the Flexible WCE Model through Artificial Time-varying Covariates Given (4) & (5), the Cox’s model in (3) becomes: (6) Once Dj(u), j=1, …m, are calculated for each u = un-censored event time, the model in (6) can be implemented using standard software for Cox’s model with

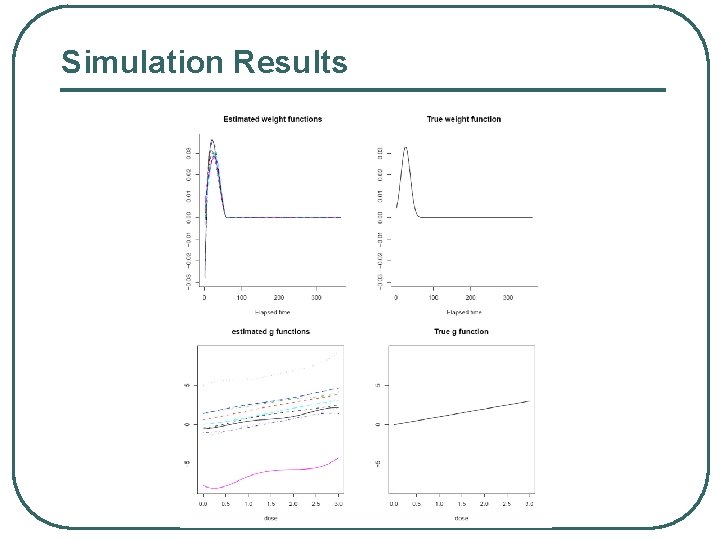
Simulation Results

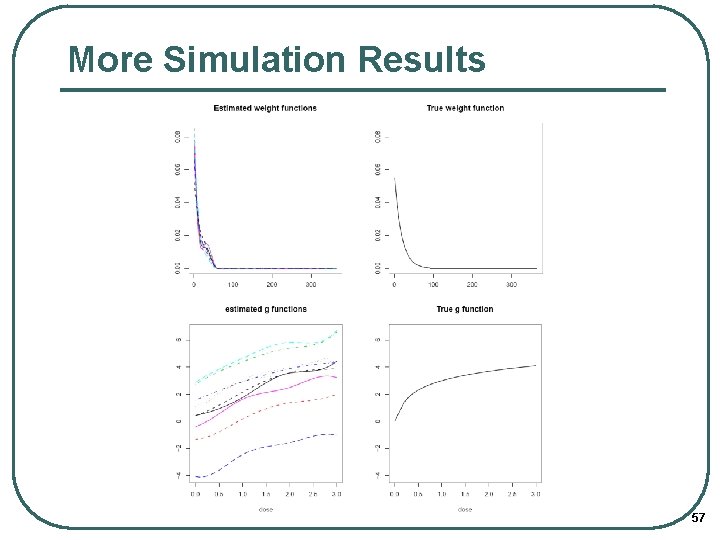
More Simulation Results 57
 Quelle methode pour arrêter les fuites urinaires la nuit
Quelle methode pour arrêter les fuites urinaires la nuit Hepaclem et constipation
Hepaclem et constipation Les effets de commerce
Les effets de commerce Hyperhédonie définition
Hyperhédonie définition Clomipramine toc
Clomipramine toc Les effets de la louange en actes 16 25-26
Les effets de la louange en actes 16 25-26 Atripla effets secondaires
Atripla effets secondaires Contrat didactique et contrat pédagogique
Contrat didactique et contrat pédagogique Ezetimbre
Ezetimbre Resyl plus effets secondaires
Resyl plus effets secondaires Effet mésomère attracteur
Effet mésomère attracteur Synerboost effets secondaires
Synerboost effets secondaires Cholangiohépatite chat
Cholangiohépatite chat Abilify effets positifs
Abilify effets positifs échéance commune
échéance commune Beano effets secondaires
Beano effets secondaires Effet inductif donneur et attracteur
Effet inductif donneur et attracteur Des des des
Des des des Robin des bois des alpes
Robin des bois des alpes 6 modes verbaux
6 modes verbaux Volume correspondant à une division
Volume correspondant à une division Des in network security
Des in network security Affiche plan marshall
Affiche plan marshall Cartographie des risques gestion des stocks
Cartographie des risques gestion des stocks La diffusion des idées des lumières
La diffusion des idées des lumières Budget des ventes
Budget des ventes Diversification des espaces et des acteurs de la production
Diversification des espaces et des acteurs de la production Je t'offrirai des fleurs et des nappes en couleurs
Je t'offrirai des fleurs et des nappes en couleurs Il existe des personnes qui sont des lumières pour tous
Il existe des personnes qui sont des lumières pour tous Volume d'un corps
Volume d'un corps Esise gresa
Esise gresa Das stufenalter des menschen
Das stufenalter des menschen Kaufhaus des bundes
Kaufhaus des bundes Représentation des 230 groupes d'espace
Représentation des 230 groupes d'espace Des cryptography
Des cryptography Affaire des placards
Affaire des placards Cahier des charges logistique
Cahier des charges logistique Marche generale des operation
Marche generale des operation Gestion des déchets au laboratoire de microbiologie
Gestion des déchets au laboratoire de microbiologie Série d'activité des métaux
Série d'activité des métaux Je veux des images
Je veux des images Impacide
Impacide Katanga syndrome
Katanga syndrome éthique des vertus
éthique des vertus Faculté des sciences exactes constantine
Faculté des sciences exactes constantine Bembel des todes
Bembel des todes La gestion internationale des ressources humaines
La gestion internationale des ressources humaines Des lauselühend
Des lauselühend Qui est virginia henderson
Qui est virginia henderson équation des télégraphistes
équation des télégraphistes Reconnaissance visuelle des objets
Reconnaissance visuelle des objets Réseau des émetteurs français
Réseau des émetteurs français La musique est la langue des émotions
La musique est la langue des émotions Tripolarisation des échanges
Tripolarisation des échanges Peirce semiotisches dreieck
Peirce semiotisches dreieck Identification des dangers
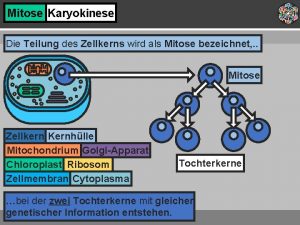
Identification des dangers Teilung des zellkerns
Teilung des zellkerns Fonctions des engrenages
Fonctions des engrenages