Modello dati ALBERO Albero insieme di punti chiamati

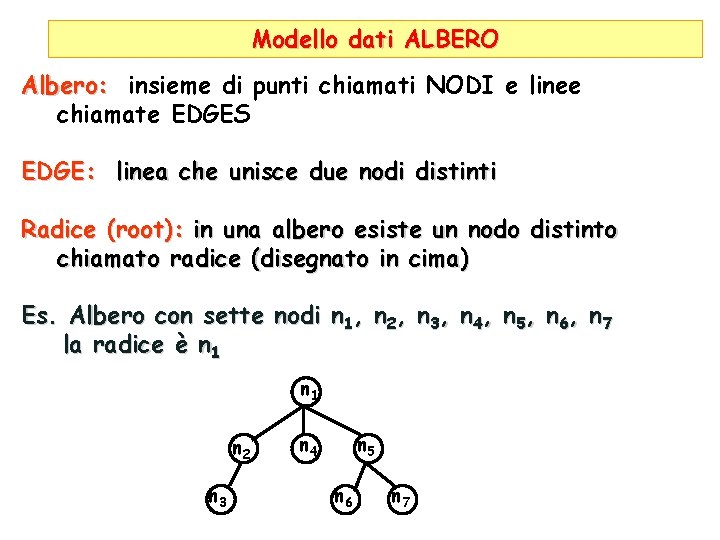
Modello dati ALBERO Albero: insieme di punti chiamati NODI e linee chiamate EDGES EDGE: linea che unisce due nodi distinti Radice (root): in una albero esiste un nodo distinto chiamato radice (disegnato in cima) Es. Albero con sette nodi n 1, n 2, n 3, n 4, n 5, n 6, n 7 la radice è n 1 n 2 n 3 n 4 n 5 n 6 n 7

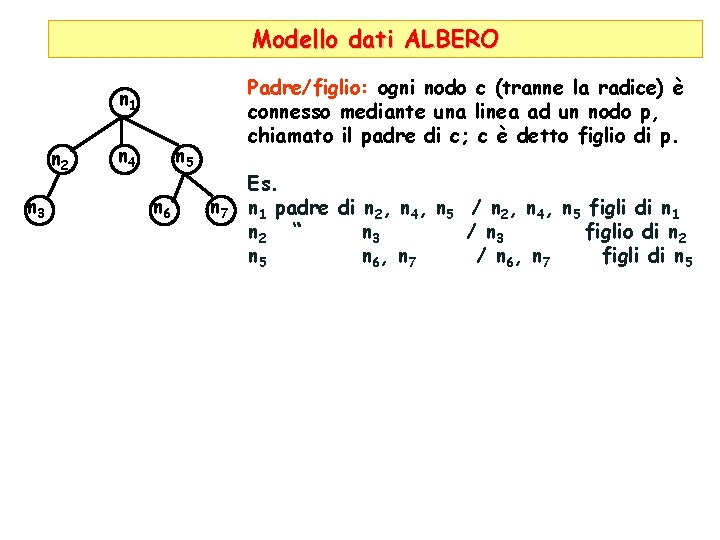
Modello dati ALBERO Padre/figlio: ogni nodo c (tranne la radice) è connesso mediante una linea ad un nodo p, chiamato il padre di c; c è detto figlio di p. n 1 n 2 n 3 n 4 n 5 n 6 n 7 Es. n 1 padre di n 2, n 4, n 5 / n 2, n 4, n 5 figli di n 1 n 2 “ n 3 / n 3 figlio di n 2 n 5 n 6, n 7 / n 6, n 7 figli di n 5

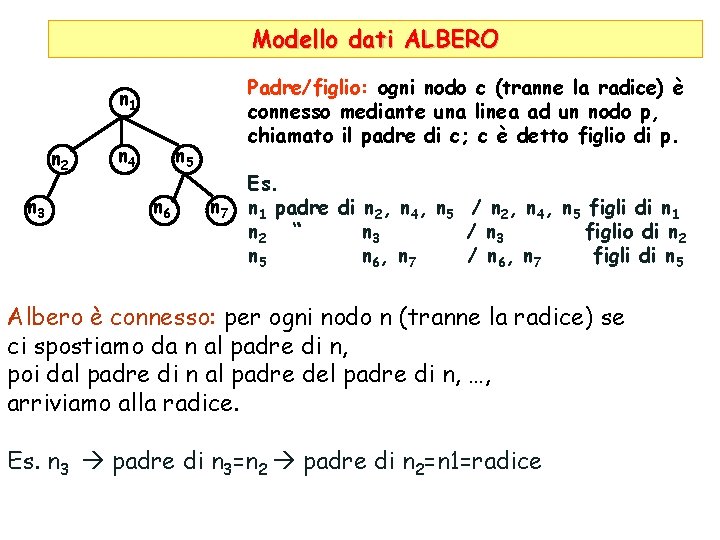
Modello dati ALBERO Padre/figlio: ogni nodo c (tranne la radice) è connesso mediante una linea ad un nodo p, chiamato il padre di c; c è detto figlio di p. n 1 n 2 n 3 n 4 n 5 n 6 n 7 Es. n 1 padre di n 2, n 4, n 5 / n 2, n 4, n 5 figli di n 1 n 2 “ n 3 / n 3 figlio di n 2 n 5 n 6, n 7 / n 6, n 7 figli di n 5 Albero è connesso: per ogni nodo n (tranne la radice) se ci spostiamo da n al padre di n, poi dal padre di n al padre del padre di n, …, arriviamo alla radice. Es. n 3 padre di n 3=n 2 padre di n 2=n 1=radice

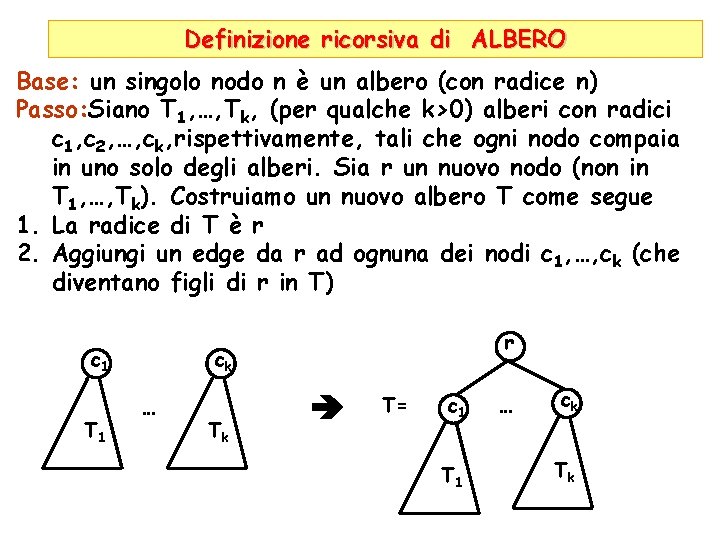
Definizione ricorsiva di ALBERO Base: un singolo nodo n è un albero (con radice n) Passo: Siano T 1, …, Tk, (per qualche k>0) alberi con radici c 1, c 2, …, ck, rispettivamente, tali che ogni nodo compaia in uno solo degli alberi. Sia r un nuovo nodo (non in T 1, …, Tk). Costruiamo un nuovo albero T come segue 1. La radice di T è r 2. Aggiungi un edge da r ad ognuna dei nodi c 1, …, ck (che diventano figli di r in T) c 1 T 1 r ck … Tk T= c 1 T 1 … ck Tk

Definizione ricorsiva di ALBERO Base: un singolo nodo n è un albero (con radice n) Passo: Siano T 1, …, Tk, (per qualche k>0) alberi con radici c 1, c 2, …, ck, rispettivamente, tali che ogni nodo compaia in un solo albero. Sia r un nuovo nodo. Costruiamo il nuovo albero T 1. La radice di T è r 2. Aggiungi un edge da r ad ognuna dei nodi c 1, …, ck (figli di r in T) Es. n 3 n 2 albero n 3 è albero

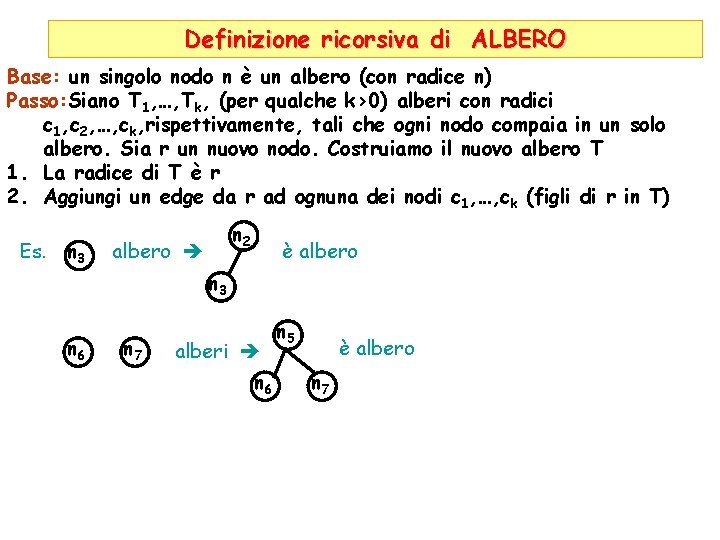
Definizione ricorsiva di ALBERO Base: un singolo nodo n è un albero (con radice n) Passo: Siano T 1, …, Tk, (per qualche k>0) alberi con radici c 1, c 2, …, ck, rispettivamente, tali che ogni nodo compaia in un solo albero. Sia r un nuovo nodo. Costruiamo il nuovo albero T 1. La radice di T è r 2. Aggiungi un edge da r ad ognuna dei nodi c 1, …, ck (figli di r in T) Es. n 3 n 2 albero è albero n 3 n 6 n 7 alberi n 6 n 5 è albero n 7

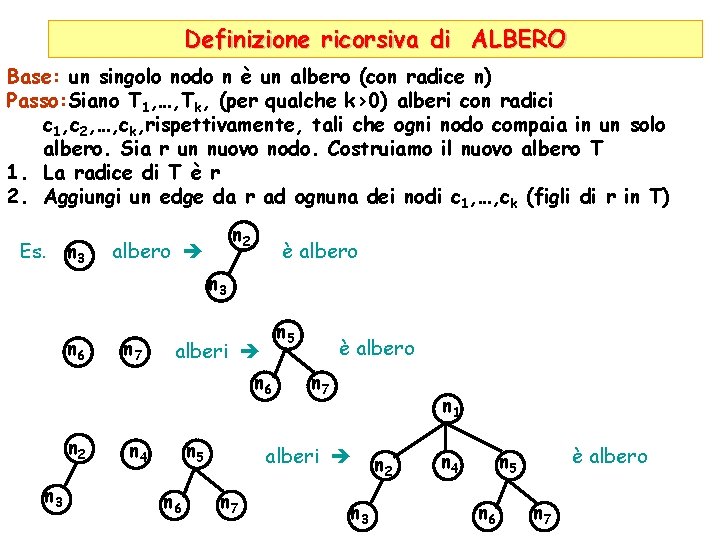
Definizione ricorsiva di ALBERO Base: un singolo nodo n è un albero (con radice n) Passo: Siano T 1, …, Tk, (per qualche k>0) alberi con radici c 1, c 2, …, ck, rispettivamente, tali che ogni nodo compaia in un solo albero. Sia r un nuovo nodo. Costruiamo il nuovo albero T 1. La radice di T è r 2. Aggiungi un edge da r ad ognuna dei nodi c 1, …, ck (figli di r in T) Es. n 3 n 2 albero è albero n 3 n 6 n 7 n 5 alberi n 6 n 2 n 3 n 4 n 5 n 6 è albero n 7 n 1 alberi n 7 n 3 n 2 n 4 è albero n 5 n 6 n 7

Definizioni su ALBERI è Dato T con radice r m 1, …mk: è un cammino (di lunghezza k-1) in T se m 1 è padre di m 2, m 2 è padre di m 3, …, mk-1 padre di mk. un solo nodo è un cammino di lunghezza 0 (k=1). n 1 n 2 n 3 n 4 n 5 n 6 n 7

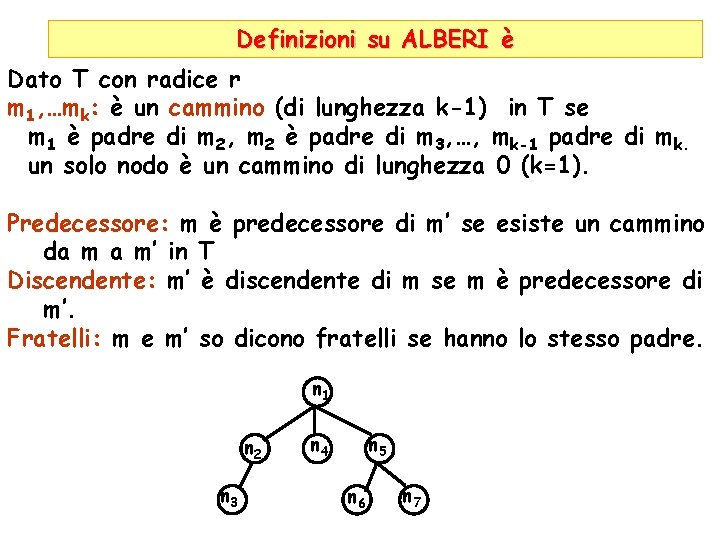
Definizioni su ALBERI è Dato T con radice r m 1, …mk: è un cammino (di lunghezza k-1) in T se m 1 è padre di m 2, m 2 è padre di m 3, …, mk-1 padre di mk. un solo nodo è un cammino di lunghezza 0 (k=1). Predecessore: m è predecessore di m’ se esiste un cammino da m a m’ in T Discendente: m’ è discendente di m se m è predecessore di m’. Fratelli: m e m’ so dicono fratelli se hanno lo stesso padre. n 1 n 2 n 3 n 4 n 5 n 6 n 7

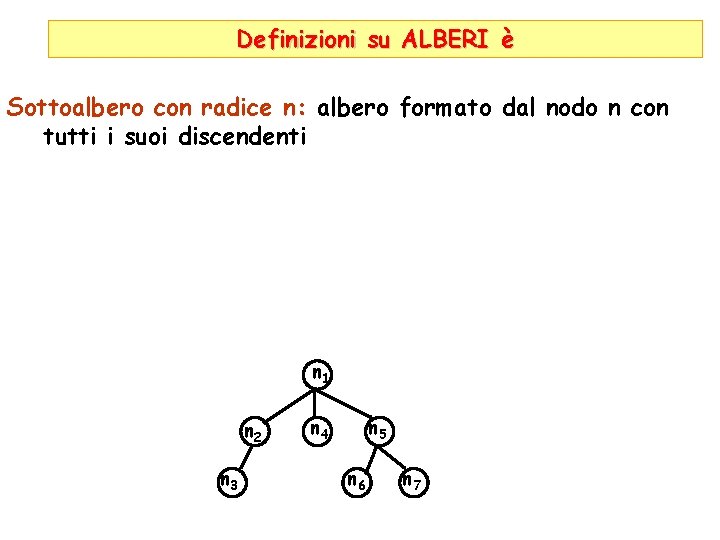
Definizioni su ALBERI è Sottoalbero con radice n: albero formato dal nodo n con tutti i suoi discendenti n 1 n 2 n 3 n 4 n 5 n 6 n 7

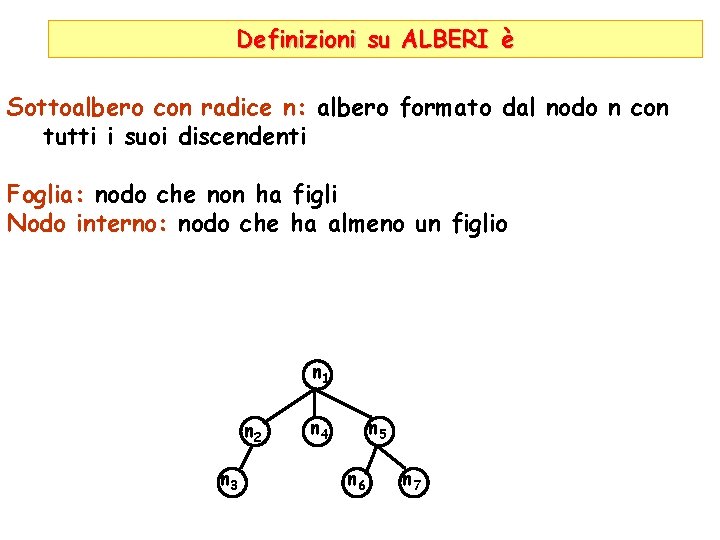
Definizioni su ALBERI è Sottoalbero con radice n: albero formato dal nodo n con tutti i suoi discendenti Foglia: nodo che non ha figli Nodo interno: nodo che ha almeno un figlio n 1 n 2 n 3 n 4 n 5 n 6 n 7

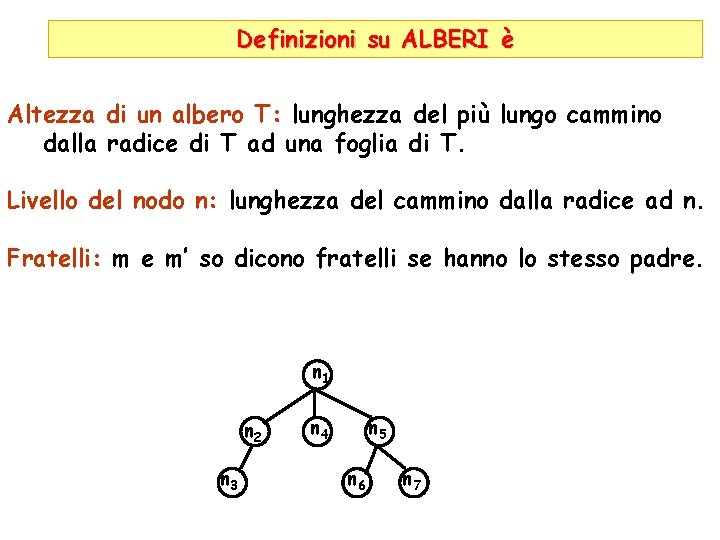
Definizioni su ALBERI è Altezza di un albero T: lunghezza del più lungo cammino dalla radice di T ad una foglia di T. Livello del nodo n: lunghezza del cammino dalla radice ad n. Fratelli: m e m’ so dicono fratelli se hanno lo stesso padre. n 1 n 2 n 3 n 4 n 5 n 6 n 7

Definizioni su ALBERI è Alberi ordinati: possiamo assegnare un ordine da sinistra a destra ai figli di un nodo, inoltre se m ed n sono fratelli ed m è a destra di n allora ogni discendente di m è a destra di ogni discendente di n Quindi per ogni coppia di nodi vale la relazione “essere a destra”. n 1 n 2 n 3 n 4 n 5 n 6 n 7

Struttura dati per ALBERI Dipende dalle operazioni che si devono effettuare Generalmente nodi = struct elemento puntatori Array di puntatori info p 0 … pb-1 Array di puntatori ai figli del nodo b= branching factor = max numero figli per nodo Se nodo ha < b figli allora alcuni puntatori sono NULL Typedef struct NODE *p. NODE struct NODE{ int info “array di b puntatori p. NODE’’}

Struttura dati per ALBERI TRIE: Serve per memorizzare stringhe di caratteri. 1. Ogni nodo ha associata una lettera 2. La stringa rappresentata dal nodo è la sequenza di lettere sul cammino dalla radice al nodo 3. Un simbolo (+/-) dice se la stringa rappresentata dal nodo fa parte di quelle da memorizzare. Es. Vogliamo memorizzare {he, hers, his, she} (array di 26 elementi)

Struttura dati per ALBERI TRIE: Serve per memorizzare stringhe di caratteri. 1. Ogni nodo ha associata una lettera 2. La stringa rappresentata dal nodo è la sequenza di lettere sul cammino dalla radice al nodo 3. Un simbolo (+/-) dice se la stringa rappresentata dal nodo fa parte di quelle da memorizzare. Es. Vogliamo memorizzare {he, hers, his, she} (array di 26 elementi) e -

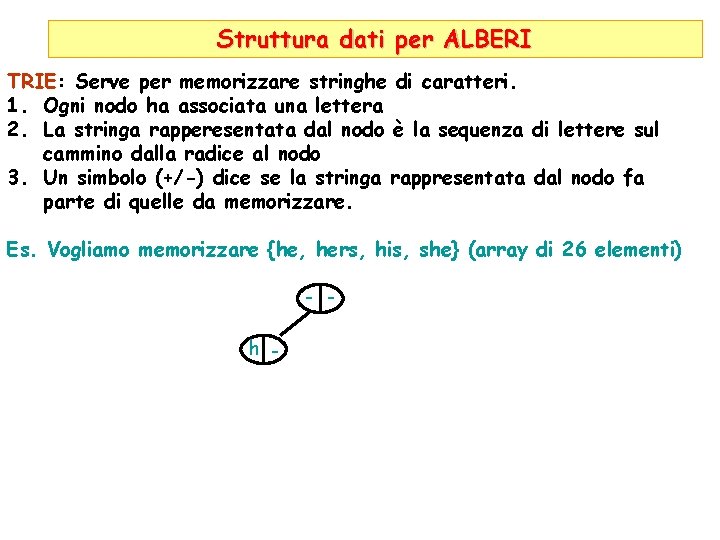
Struttura dati per ALBERI TRIE: Serve per memorizzare stringhe di caratteri. 1. Ogni nodo ha associata una lettera 2. La stringa rapperesentata dal nodo è la sequenza di lettere sul cammino dalla radice al nodo 3. Un simbolo (+/-) dice se la stringa rappresentata dal nodo fa parte di quelle da memorizzare. Es. Vogliamo memorizzare {he, hers, his, she} (array di 26 elementi) - h -

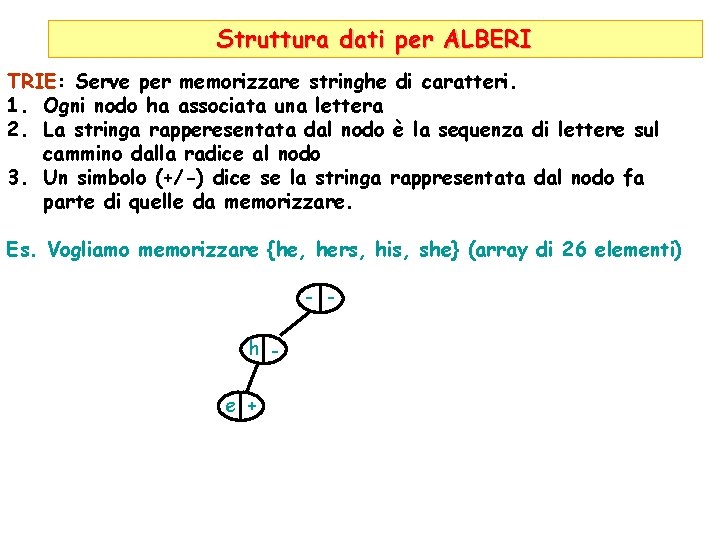
Struttura dati per ALBERI TRIE: Serve per memorizzare stringhe di caratteri. 1. Ogni nodo ha associata una lettera 2. La stringa rapperesentata dal nodo è la sequenza di lettere sul cammino dalla radice al nodo 3. Un simbolo (+/-) dice se la stringa rappresentata dal nodo fa parte di quelle da memorizzare. Es. Vogliamo memorizzare {he, hers, his, she} (array di 26 elementi) - h e +

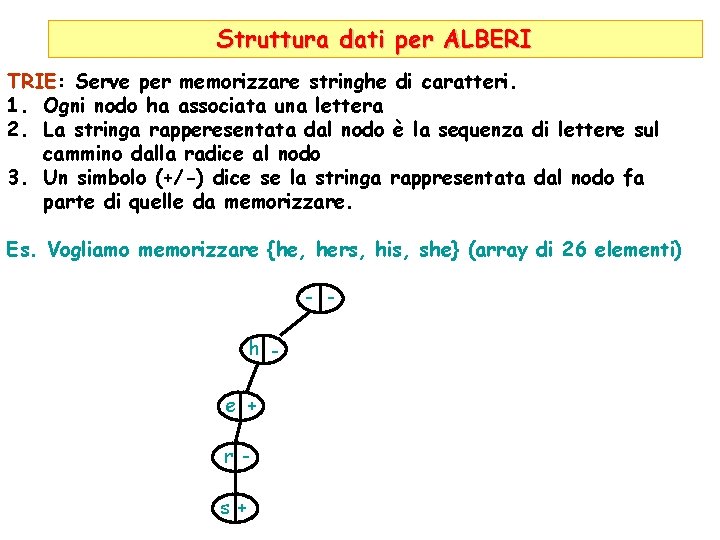
Struttura dati per ALBERI TRIE: Serve per memorizzare stringhe di caratteri. 1. Ogni nodo ha associata una lettera 2. La stringa rapperesentata dal nodo è la sequenza di lettere sul cammino dalla radice al nodo 3. Un simbolo (+/-) dice se la stringa rappresentata dal nodo fa parte di quelle da memorizzare. Es. Vogliamo memorizzare {he, hers, his, she} (array di 26 elementi) - h e + r s+

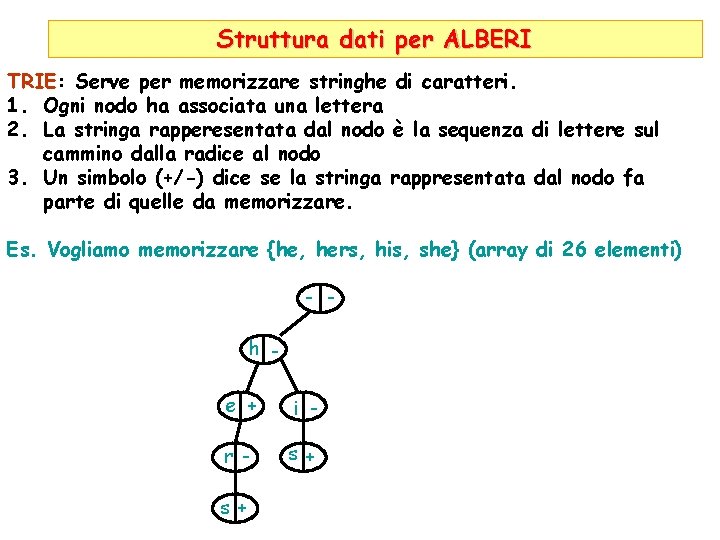
Struttura dati per ALBERI TRIE: Serve per memorizzare stringhe di caratteri. 1. Ogni nodo ha associata una lettera 2. La stringa rapperesentata dal nodo è la sequenza di lettere sul cammino dalla radice al nodo 3. Un simbolo (+/-) dice se la stringa rappresentata dal nodo fa parte di quelle da memorizzare. Es. Vogliamo memorizzare {he, hers, his, she} (array di 26 elementi) - h e + i - r - s+ s+

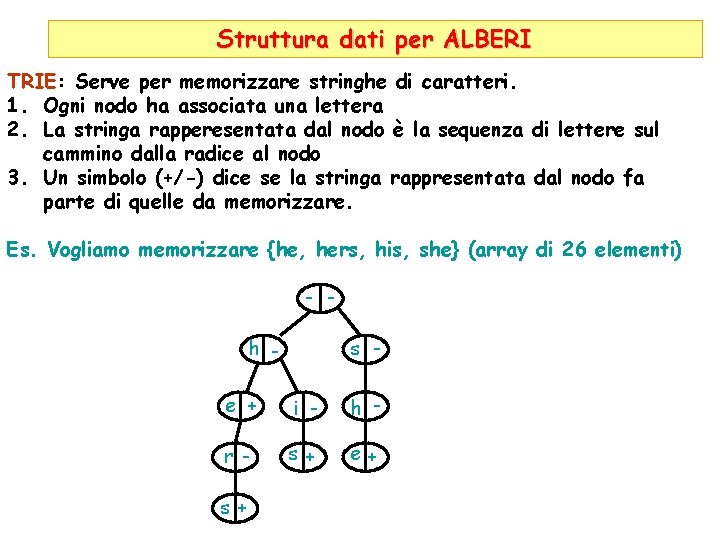
Struttura dati per ALBERI TRIE: Serve per memorizzare stringhe di caratteri. 1. Ogni nodo ha associata una lettera 2. La stringa rapperesentata dal nodo è la sequenza di lettere sul cammino dalla radice al nodo 3. Un simbolo (+/-) dice se la stringa rappresentata dal nodo fa parte di quelle da memorizzare. Es. Vogliamo memorizzare {he, hers, his, she} (array di 26 elementi) - h - s - e + i - h - r - s+ e+ s+

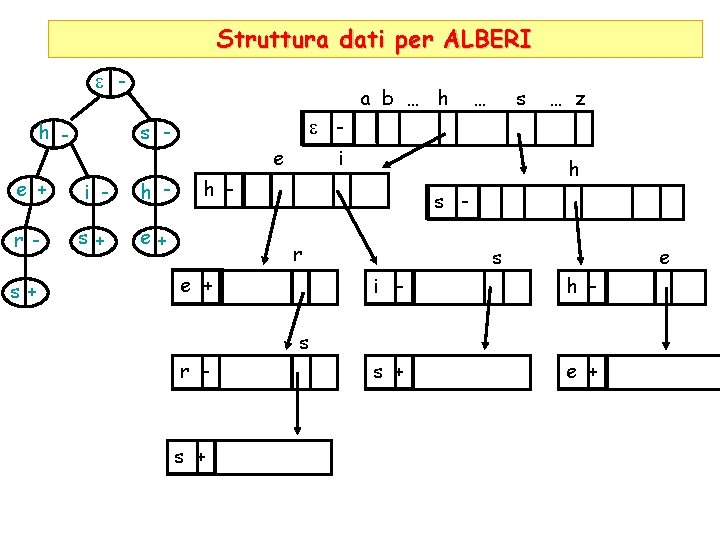
Struttura dati per ALBERI e h - a b … h i - h - r - s+ e+ s+ s … z e - s - e + … e i h h - s r e + s e i - h - s + e + s r - s +

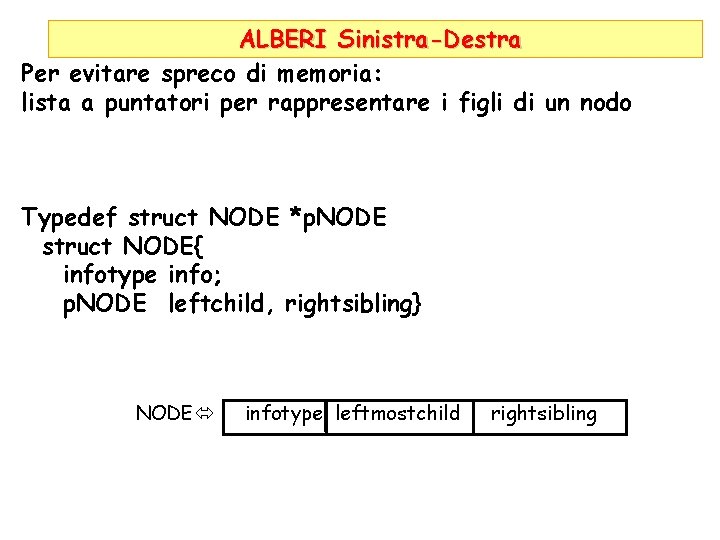
ALBERI Sinistra-Destra Per evitare spreco di memoria: lista a puntatori per rappresentare i figli di un nodo Typedef struct NODE *p. NODE struct NODE{ infotype info; p. NODE leftchild, rightsibling} NODE infotype leftmostchild rightsibling

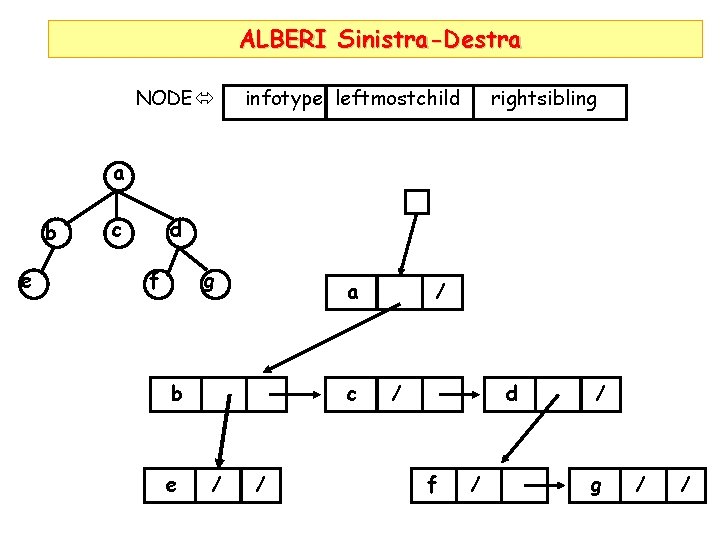
ALBERI Sinistra-Destra NODE infotype leftmostchild rightsibling a b e c d g f a b e c / / d f / / g / /

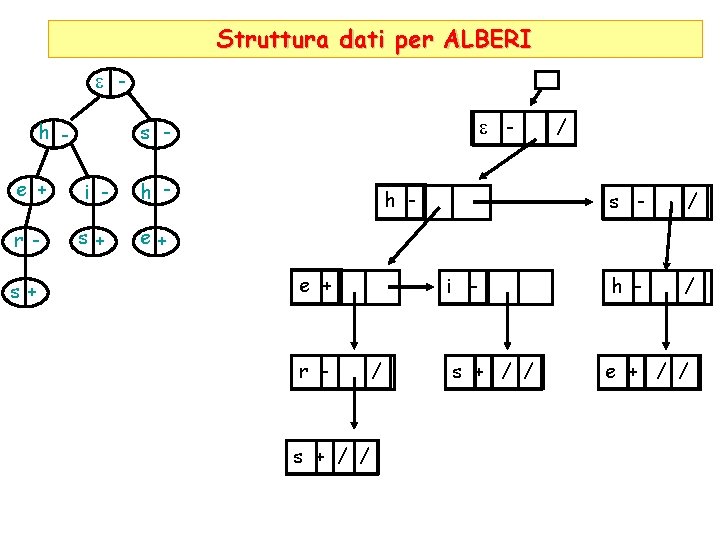
Struttura dati per ALBERI e h e + i - h - r - s+ e+ s+ e - s h - e + r - s + / / s - / i - h - / s + / / e + / /

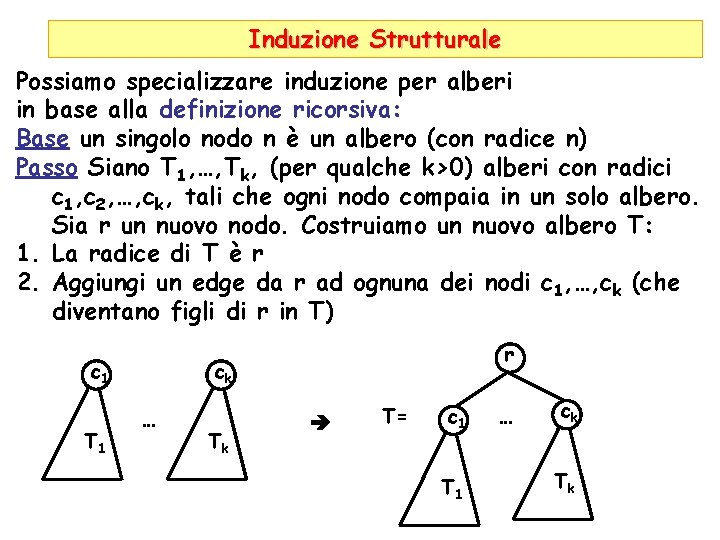
Induzione Strutturale Possiamo specializzare induzione per alberi in base alla definizione ricorsiva: Base un singolo nodo n è un albero (con radice n) Passo Siano T 1, …, Tk, (per qualche k>0) alberi con radici c 1, c 2, …, ck, tali che ogni nodo compaia in un solo albero. Sia r un nuovo nodo. Costruiamo un nuovo albero T: 1. La radice di T è r 2. Aggiungi un edge da r ad ognuna dei nodi c 1, …, ck (che diventano figli di r in T) c 1 T 1 r ck … Tk T= c 1 T 1 … ck Tk

Induzione Strutturale Vogliamo provare che l’affermazione S(T) è vera per ogni albero T Base: S(T) è vera per ogni albero con un singolo nodo r

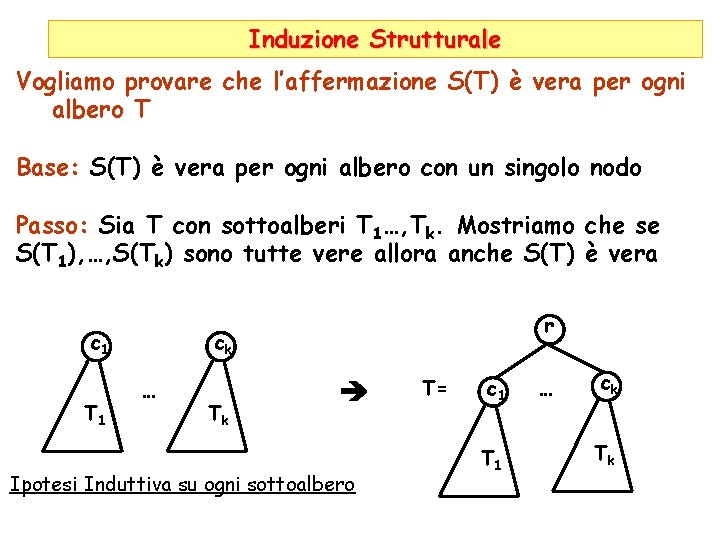
Induzione Strutturale Vogliamo provare che l’affermazione S(T) è vera per ogni albero T Base: S(T) è vera per ogni albero con un singolo nodo Passo: Sia T con sottoalberi T 1…, Tk. Mostriamo che se S(T 1), …, S(Tk) sono tutte vere allora anche S(T) è vera c 1 T 1 r ck … Tk Ipotesi Induttiva su ogni sottoalbero T= c 1 T 1 … ck Tk

Induzione Strutturale Es. Definiamo V(T)= numero di nodi di T deg(x)= numero di figli di x Vogliamo provare l’affermazione S(T):

Induzione Strutturale Es. Definiamo V(T)=numero di nodi di T e grado del nodo x =deg(x)= numero di figli di x Vogliamo provare l’affermazione S(T): BASE: Se T ha 1 nodo x, allora x non ha figli e deg(x)=0 V(T)=1=1+deg(x)

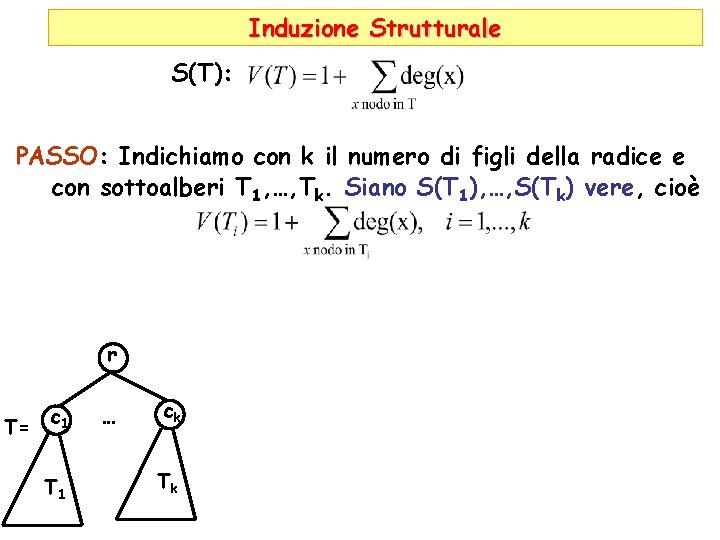
Induzione Strutturale S(T): PASSO: Indichiamo con k il numero di figli della radice e con sottoalberi T 1, …, Tk. Siano S(T 1), …, S(Tk) vere, cioè r T= c 1 T 1 … ck Tk

Induzione Strutturale S(T): PASSO: Indichiamo con k il numero di figli della radice e con sottoalberi T 1, …, Tk. Siano S(T 1), …, S(Tk) vere, cioè Proviamo S(T) r T= c 1 T 1 … ck Tk

Induzione Strutturale Induzione strutturale induzione completa specializzata per alberi S(T): proprieta P è vera S(n): proprietà P è vera per T ogni albero con n nodi Base. Albero con 1 nodo affermazione vera n=1 Passo. I. I. per ogni sottoalbero I. I. per ogni m<n proviamo per T proviamo per n

Induzione Strutturale Es. Consideriamo alberi con rappresentazione sinistra-destra Vogliamo provare l’affermazione S(T): il numero di puntatori NULL in T è V(T)+1 BASE: Se T ha 1 nodo x, allora x non ha figli ne fratelli V(T)=1, #NULL=2=V(T)+1

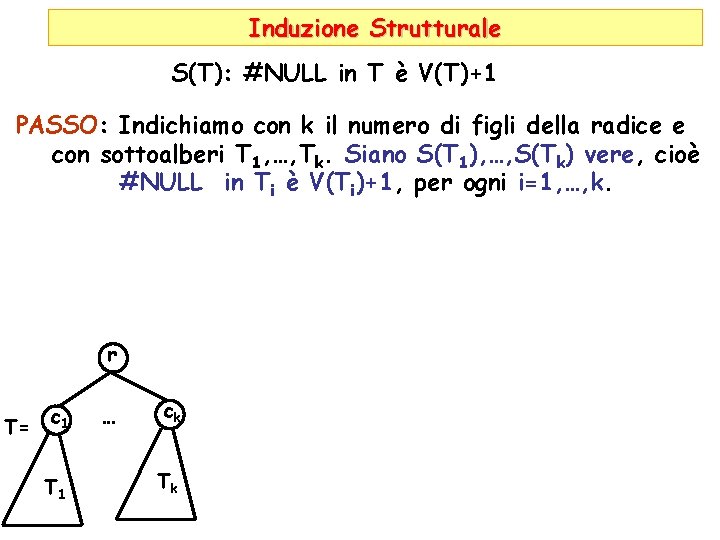
Induzione Strutturale S(T): #NULL in T è V(T)+1 PASSO: Indichiamo con k il numero di figli della radice e con sottoalberi T 1, …, Tk. Siano S(T 1), …, S(Tk) vere, cioè #NULL in Ti è V(Ti)+1, per ogni i=1, …, k. r T= c 1 T 1 … ck Tk

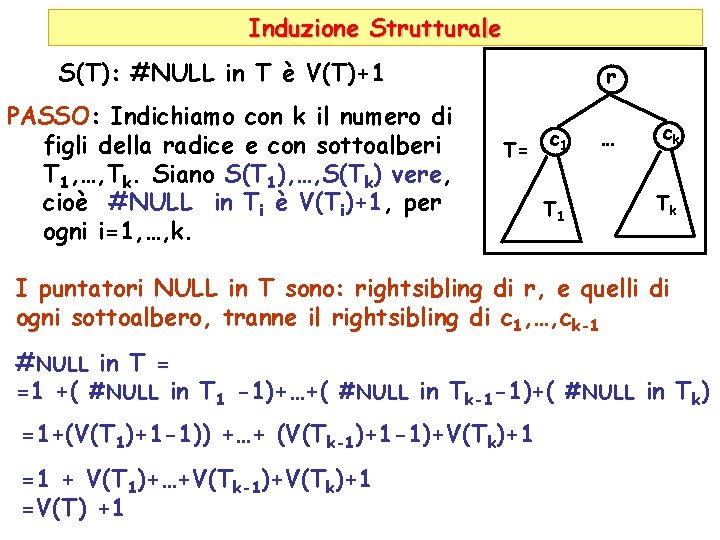
Induzione Strutturale S(T): #NULL in T è V(T)+1 PASSO: Indichiamo con k il numero di figli della radice e con sottoalberi T 1, …, Tk. Siano S(T 1), …, S(Tk) vere, cioè #NULL in Ti è V(Ti)+1, per ogni i=1, …, k. r T= c 1 T 1 … ck Tk I puntatori NULL in T sono: rightsibling di r, e quelli di ogni sottoalbero, tranne il rightsibling di c 1, …, ck-1 #NULL in T = =1 +( #NULL in T 1 -1)+…+( #NULL in Tk-1 -1)+( #NULL in Tk) =1+(V(T 1)+1 -1)) +…+ (V(Tk-1)+1 -1)+V(Tk)+1 =1 + V(T 1)+…+V(Tk-1)+V(Tk)+1 =V(T) +1

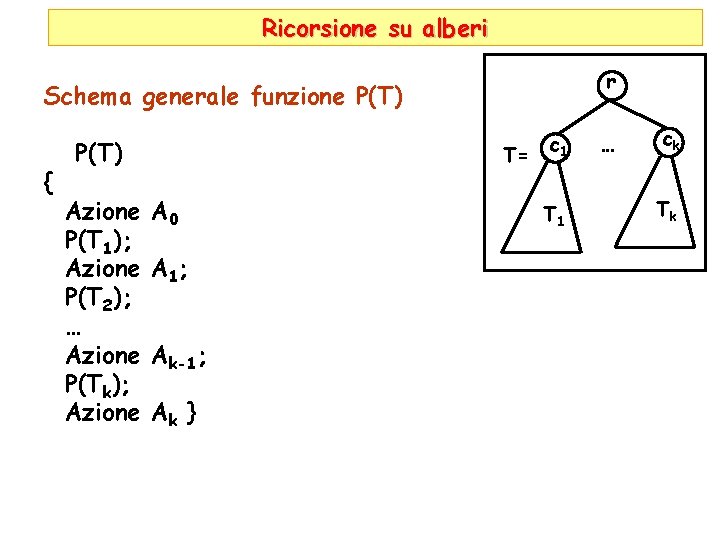
Ricorsione su alberi r Schema generale funzione P(T) { P(T) Azione P(T 1); Azione P(T 2); … Azione P(Tk); Azione T= A 0 A 1; Ak-1; Ak } c 1 T 1 … ck Tk

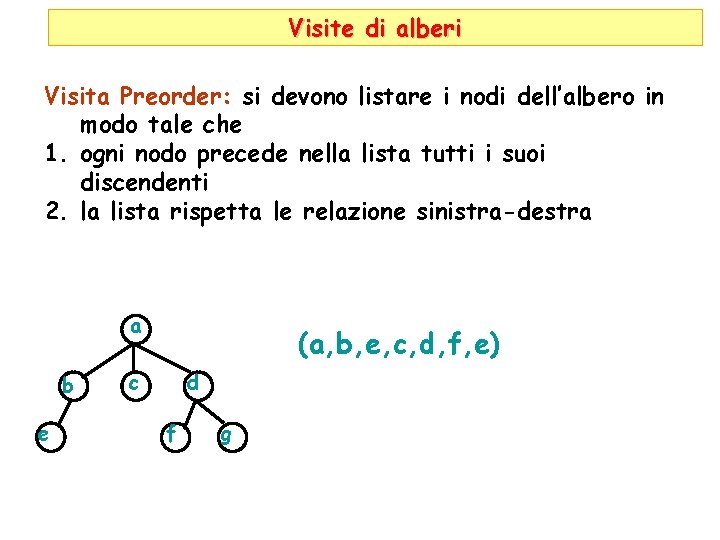
Visite di alberi Visita Preorder: si devono listare i nodi dell’albero in modo tale che 1. ogni nodo precede nella lista tutti i suoi discendenti 2. la lista rispetta le relazione sinistra-destra a b e (a, b, e, c, d, f, e) c d f g

Visite di alberi Visita Preorder: si devono listare i nodi dell’albero in modo tale che 1. ogni nodo precede nella lista tutti i suoi discendenti 2. la lista rispetta le relazione sinistra-destra r T= c 1 T 1 … ck Tk void preorder (p. Node n) { } p. NODE c; /* figlio di n*/ printf(“%cn”, n->nodelabel); c=n->leftmostchild; while (c != NULL) { preorder(c); c=c->rightsibling; } typedef struct NODE *p. NODE struct NODE { char nodelabel; p. NODE leftmostchild, rigthsibling; }

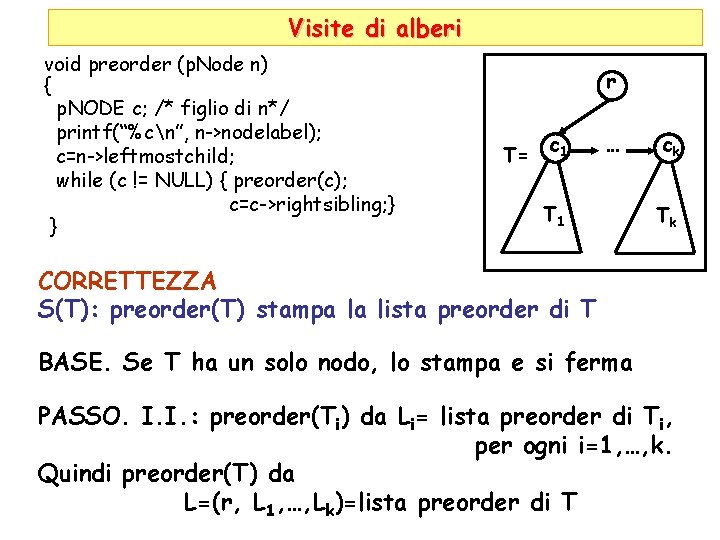
Visite di alberi void preorder (p. Node n) { p. NODE c; /* figlio di n*/ printf(“%cn”, n->nodelabel); c=n->leftmostchild; while (c != NULL) { preorder(c); c=c->rightsibling; } } r T= c 1 … T 1 ck Tk CORRETTEZZA S(T): preorder(T) stampa la lista preorder di T BASE. Se T ha un solo nodo, lo stampa e si ferma PASSO. I. I. : preorder(Ti) da Li= lista preorder di Ti, per ogni i=1, …, k. Quindi preorder(T) da L=(r, L 1, …, Lk)=lista preorder di T

Visite di alberi void preorder (p. Node n) { p. NODE c; /* figlio di n*/ printf(“%cn”, n->nodelabel); c=n->leftmostchild; while (c != NULL) { preorder(c); c=c->rightsibling; } } r T= R. T. : O(n), dove n è il numero di nodi di T T(1)=O(1) T(n)= O(1) + O(n 1)+…+O(nk) = O(n) dove n=1+n 1+…+nk c 1 T 1 … ck Tk

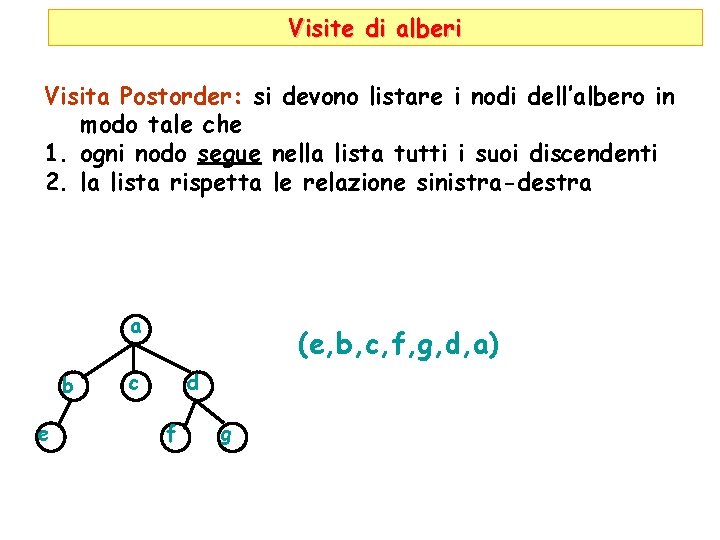
Visite di alberi Visita Postorder: si devono listare i nodi dell’albero in modo tale che 1. ogni nodo segue nella lista tutti i suoi discendenti 2. la lista rispetta le relazione sinistra-destra a b e (e, b, c, f, g, d, a) c d f g

Visite di alberi Visita Postorder: si devono listare i nodi dell’albero in modo tale che 1. ogni nodo segue nella lista tutti i suoi discendenti 2. la lista rispetta le relazione sinistra-destra void postorder (p. Node n) { } p. NODE c; /* figlio di n*/ c=n->leftmostchild; while (c != NULL) {postorder(c); c=c>rightsibling; } printf(“%cn”, n->nodelabel); r T= c 1 T 1 … ck Tk

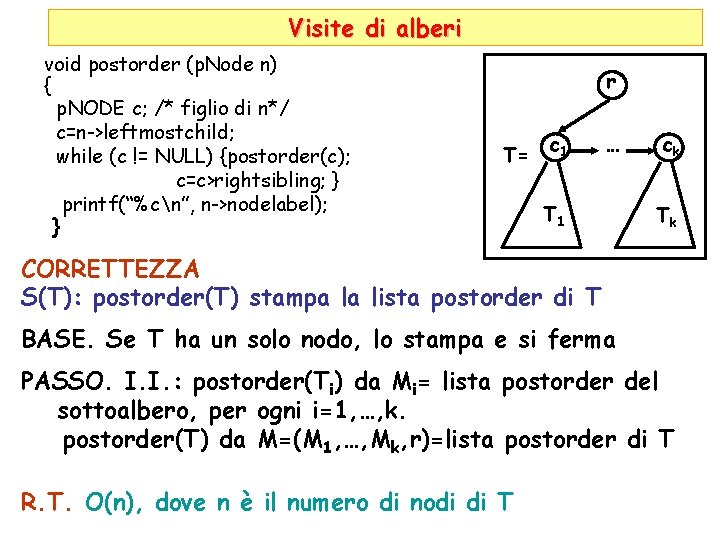
Visite di alberi void postorder (p. Node n) { p. NODE c; /* figlio di n*/ c=n->leftmostchild; while (c != NULL) {postorder(c); c=c>rightsibling; } printf(“%cn”, n->nodelabel); } r T= c 1 … T 1 ck Tk CORRETTEZZA S(T): postorder(T) stampa la lista postorder di T BASE. Se T ha un solo nodo, lo stampa e si ferma PASSO. I. I. : postorder(Ti) da Mi= lista postorder del sottoalbero, per ogni i=1, …, k. postorder(T) da M=(M 1, …, Mk, r)=lista postorder di T R. T. O(n), dove n è il numero di nodi di T

Computo dell’ Altezza di un albero Altezza di un nodo n= max distanza di n da una foglia sua discendente Altezza albero= altezza radice Altezza di una foglia = 0 Altezza di un nodo interno n = 1 + (altezza sottoalbero radicato in n) = 1 + max altezza figli di n a b e c d f Altezza di a = 1 + max { altezza di b, altezza di c, altezza di d } = 1 + max { 1, 0, 1} =1+1=2 g

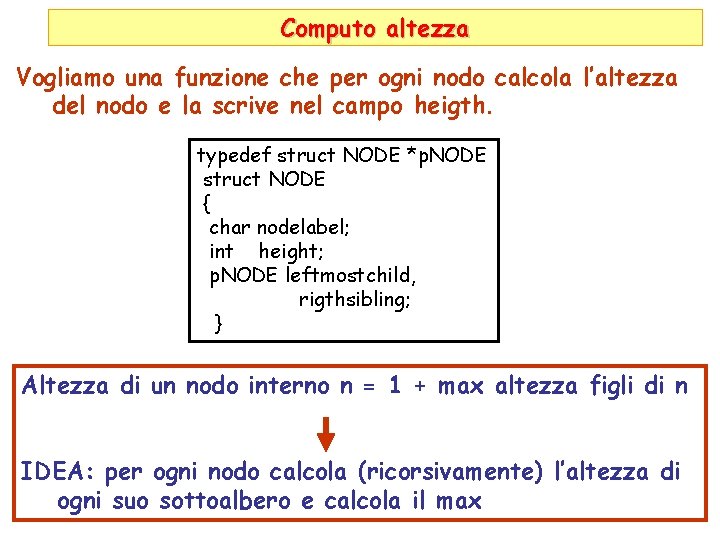
Computo altezza Vogliamo una funzione che per ogni nodo calcola l’altezza del nodo e la scrive nel campo heigth. typedef struct NODE *p. NODE struct NODE { char nodelabel; int height; p. NODE leftmostchild, rigthsibling; } Altezza di un nodo interno n = 1 + max altezza figli di n IDEA: per ogni nodo calcola (ricorsivamente) l’altezza di ogni suo sottoalbero e calcola il max

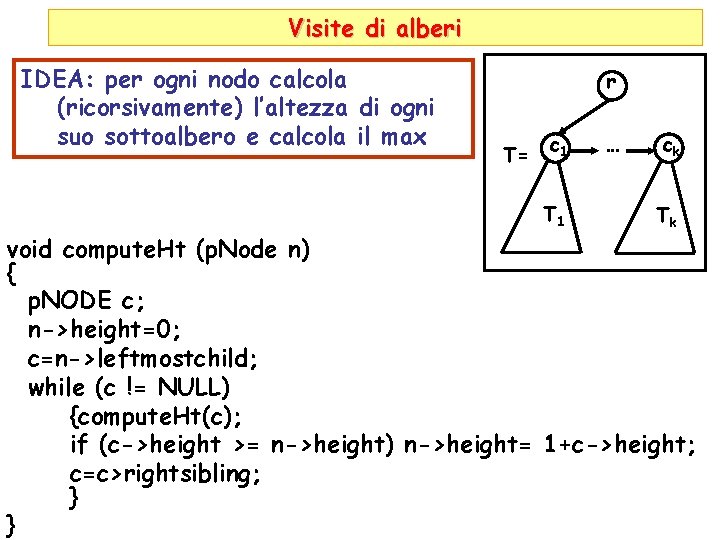
Visite di alberi IDEA: per ogni nodo calcola (ricorsivamente) l’altezza di ogni suo sottoalbero e calcola il max r T= c 1 T 1 … ck Tk void compute. Ht (p. Node n) { p. NODE c; n->height=0; c=n->leftmostchild; while (c != NULL) {compute. Ht(c); if (c->height >= n->height) n->height= 1+c->height; c=c>rightsibling; } }

Computo altezza void compute. Ht (p. Node n) { p. NODE c; n->height=0; c=n->leftmostchild; while (c != NULL) {compute. Ht(c); if (c->height >= n->height) n->height= 1+c->height; c=c>rightsibling; } } CORRETTEZZA S(T): compute. Ht(n) calcola correttamente altezza nodo n BASE. Se T ha un solo nodo, pone height=0 e si ferma

Computo altezza void compute. Ht (p. Node n) { p. NODE c; n->height=0; c=n->leftmostchild; while (c != NULL) {compute. Ht(c); if (c->height >= n->height) n->height= 1+c->height; c=c>rightsibling; } } CORRETTEZZA S(T): compute. Ht(n) calcola correttamente altezza nodo n BASE. Se T ha un solo nodo, pone height=0 e si ferma PASSO. I. I. : compute. Ht(ni) calcola correttamente l’altezza del figlio ni di n, per ogni i=1, …, k. n->heigth= max{1+ n 1 ->height, …, 1+ nk->height} = max{1+ altezza T 1, , …, 1+ altezza Tk} (per I. I) = 1 + max altezza sottoalberi

Alberi Binari Ogni nodo ha < 2 figli: figlio destro, figlio sinistro a d b e f g c

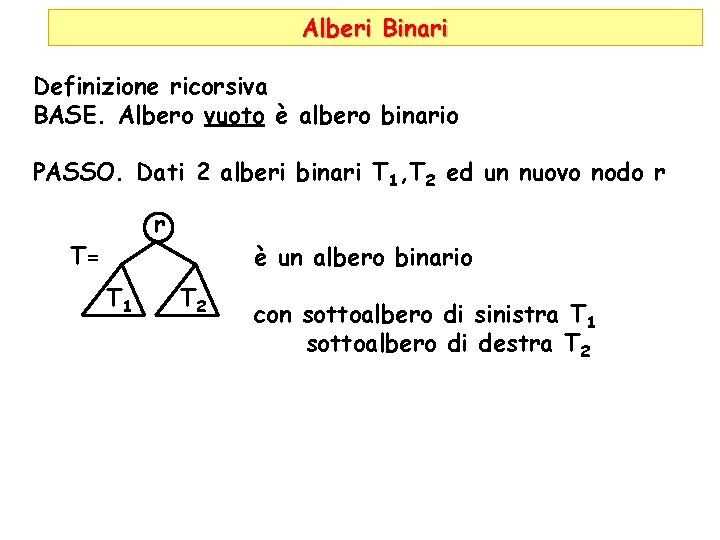
Alberi Binari Definizione ricorsiva BASE. Albero vuoto è albero binario PASSO. Dati 2 alberi binari T 1, T 2 ed un nuovo nodo r r T= T 1 è un albero binario T 2 con sottoalbero di sinistra T 1 sottoalbero di destra T 2

Alberi Binari Bastano due puntatori per nodo: figlio destro, figlio sinistro Struttura dati Typedef struct NODE *TREE struct NODE{ etype nodelabel; TREE leftchild, rightchild; }

Ricorsione su Alberi Binari FUNZIONE (T TREE) { Azione A 0 FUNZIONE(T 1) Azione A 1; FUNZIONE(T 2) Azione A 2; }

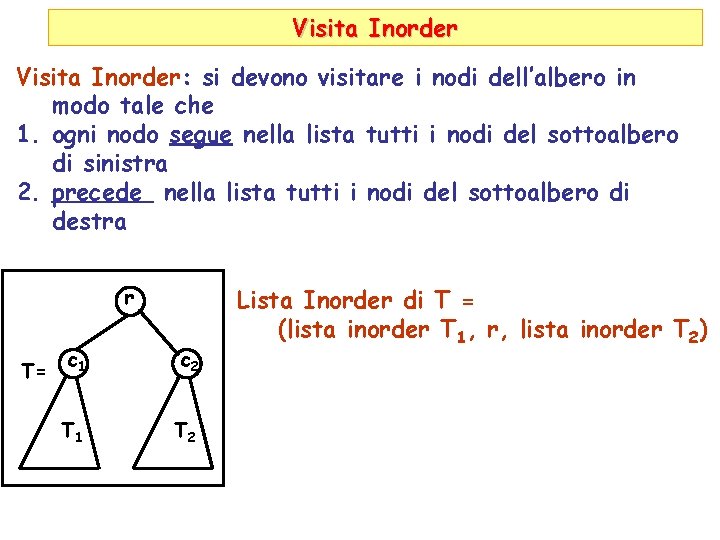
Visita Inorder: si devono visitare i nodi dell’albero in modo tale che 1. ogni nodo segue nella lista tutti i nodi del sottoalbero di sinistra 2. precede nella lista tutti i nodi del sottoalbero di destra r T= c 1 c 2 T 1 T 2 Lista Inorder di T = (lista inorder T 1, r, lista inorder T 2)

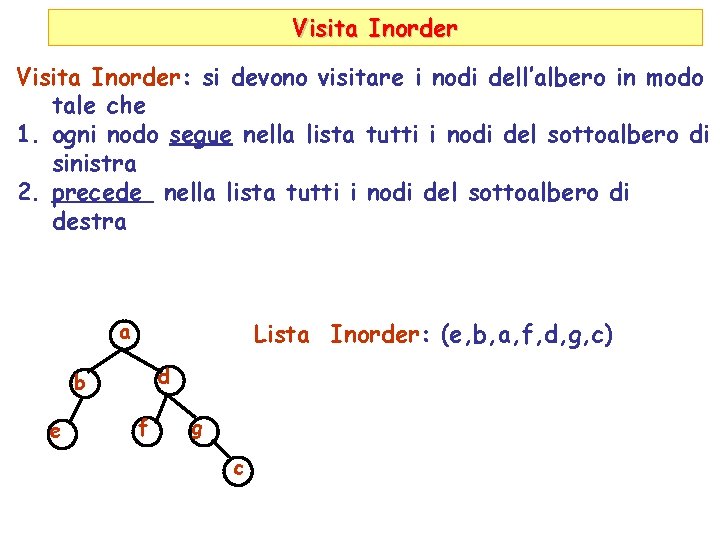
Visita Inorder: si devono visitare i nodi dell’albero in modo tale che 1. ogni nodo segue nella lista tutti i nodi del sottoalbero di sinistra 2. precede nella lista tutti i nodi del sottoalbero di destra Lista Inorder: (e, b, a, f, d, g, c) a d b e f g c

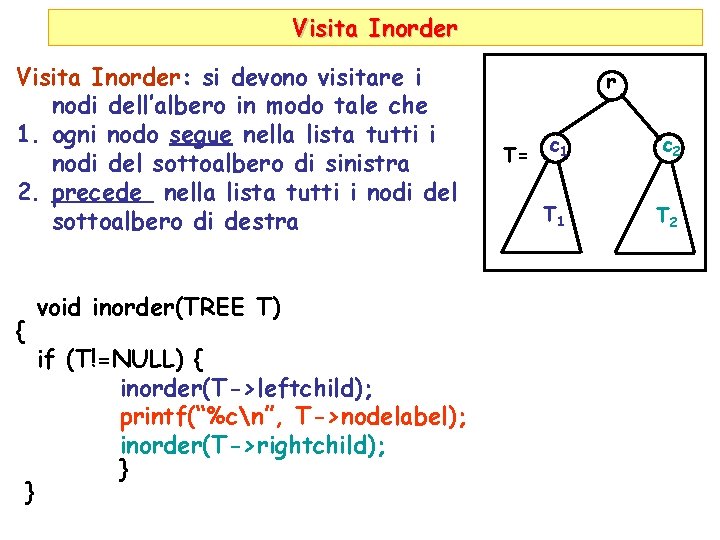
Visita Inorder: si devono visitare i nodi dell’albero in modo tale che 1. ogni nodo segue nella lista tutti i nodi del sottoalbero di sinistra 2. precede nella lista tutti i nodi del sottoalbero di destra void inorder(TREE T) { } if (T!=NULL) { inorder(T->leftchild); printf(“%cn”, T->nodelabel); inorder(T->rightchild); } r T= c 1 c 2 T 1 T 2

Visita Inorder void inorder(TREE T) { } if (T!=NULL) { inorder(T->leftchild); printf(“%cn”, T->nodelabel); inorder(T->rightchild); } Inorder: e, b, a, f, d, g, c a d b e f g c