METODE NUMERIK 3 SKS STMIK CILEGON PENGANTAR NUMERIK

METODE NUMERIK (3 SKS) STMIK CILEGON

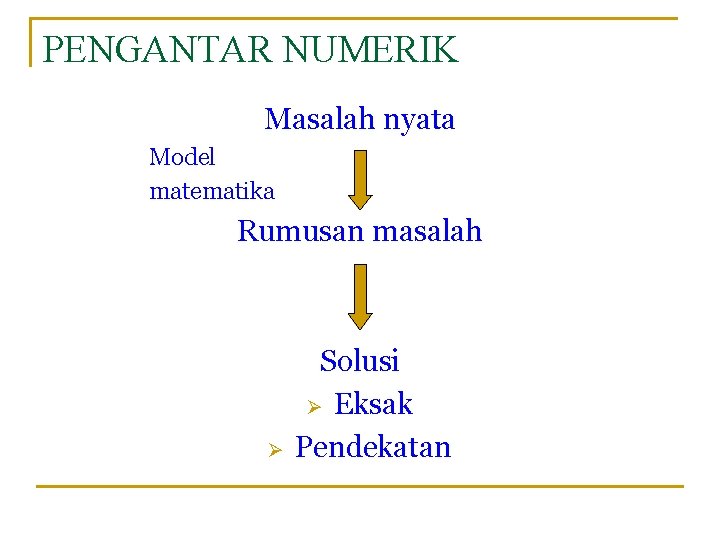
PENGANTAR NUMERIK Masalah nyata Model matematika Rumusan masalah Ø Solusi Ø Eksak Pendekatan

Contoh kasus. 1. 2. Pemakaian rumus ABC utuk menentukan akar dari persamaan kuadrat contoh f(x) = x 2 + 1015 x + 5 = 0 Menentukan determinan dari suatu matriks Contoh.

Metode analitik vs Metode numerik o Metode analitik - menghasilkan solusi eksak (galat = 0) - menghasilkan solusi dalam bentuk fungsi matematika o Metode numerik - menghasilkan solusi pendekatan - menghasilkan solusi dalam bentuk angka

Peranan komputer dalam Met. Num Mempercepat perhitungan tanpa membuat kesalahan l Mencoba berbagai kemungkinan yang terjadi akibat perubahan parameter Contoh aplikasi : Mathlab, Mathcad, Mathematica dll Mengapa perlu belajar Metnum 1. Alat bantu yang ampuh (tidak dapat diselesaikan secara analitik) 2. Memudahkan dalam memahami aplikasi program 3. Dapat membuat sendiri program komputer yang tidak dapat diselesaikan dengan program aplikasi 4. Menyederhanakan matematika yang lebih tinggi menjadi operasi matematika yang mendasar l

Prinsip perhitungan dalam numerik l l Penggunaan metode/algoritma yang tepat sesuai kasus “tidak ada algoritma untuk segalanya” Mencari solusi pendekatan yang diperoleh dengan cepat dan error kecil

Penyajian bilangan Bilangan ada 2: 1. 2. Eksak Tidak eksak q q Perhitungan matematika tidak eksak , e, Perhitungan desimal yang berulang 0. 3333…. Hasil perhitungan deret tak hingga e Hasil pengukuran

Floating point n f. p x = a x bn ¡ a = matise (0 ≤ a ≤ 1) ¡ b = basis ¡ n = eksponen (bilangan bulat) Dalam alat hitung elektronik biasanya digunakan basis b = 10

Desimal dan angka signifikan o Misal x = 0. 05 2 desimal 1 angka signifikan x = 0. 30 2 desimal 2 angka signifikan Angka signifikan adalah angka 0 yang diabaikan untuk yang berada dibelakang sedangkan dihitung untuk angka 0 yang berada di depan

Aritmatika dalam floating point ¡ Penjumlahan /pengurangan l Ubah bilangan ke f. p l Ubah eksponen mengikuti eksponen yang besar l Jumlahkan/kurangkan l Sesuaikan desimal/a. s yang diminta Contoh. x = 123. 75 dan y = 0. 14 (2 desimal) x = 0. 12375 x 103 = 0. 12 x 103 y = 0. 14 = 0. 00014 x 103 = 0. 00 x 103 x + y = 0. 12 x 103 + 0. 00 x 103= 0. 12 x 103 = 120

n Perkalian/pembagian q Ubah bilangan ke f. p q Untuk perkalian : jumlahkan eksponen dan kalikan matise q Untuk pembagian : kurangkan eksponen dan bagikan matise q Tulis hasil dalam f. p sesuai dengan desimal yang diminta Contoh. x = 123. 75 dan y = 0. 14 (2 desimal) x = 0. 12375 x 103 = 0. 12 x 103 y = 0. 14 x 100 x. y = (0. 12 x 103). (0. 14 x 100)= 0. 0168 x 103 = 0. 02 x 103 = 20

• Alur perhitungan Input Proses Output Sumber-sumber galat : • Galat yang ada pada input : – Chopping error – Rounding error – Bilangan yang dimasukkan bukan bilangan eksak

¢ ¢ Galat yang ada proses : l Rambatan galat l Rumus/metode/algoritma tidak tepat l Kesalahan alat l Human error Galat pada output : l Chopping error l Rounding error

Ø Ø Ø Misal x adalah nilai eksak dan x* adalah nilai pendekatan maka galat = x – x* Galat absolut a = |x – x*| Galat absolut relatif

Macam-macam galat 1. Chopping error Galat yang terjadi akibat proses pemenggalan angka sesuai desimal yang diminta Contoh. x = 0. 378456 x 103 dipenggal hingga tiga desimal x* = 0. 378 x 103 galat a = |x – x*| = |0. 378456 x 103 – 0. 378 x 103| = 0. 000456 x 103 = 0. 456

2. Round off error Galat yang terjadi akibat membulatkan suatu nilai Contoh. x = 0. 378546 x 103 dibulatkan menjadi 3 desimal x* = 0. 379 x 103 galat a = |x – x*| = |0. 378546 x 103 – 0. 379 x 103| = 0. 000454 x 103 = 0. 454

3. Truncation error Galat yang muncul akibat pemotongan proses hitung tak hingga, misal deret Taylor, deret Mac. Laurin Contoh.

Nested form l l Nested form menjadikan operasi perhitungan lebih efisien dapat meminimalisasi galat Contoh. f(x) = 3 + 2. 5 x + 5. 35 x 2 – 4 x 3 f(0. 25) = 4. 521875 l l l Nested form f(x) = 3 + x(2. 5+x(5. 35+x(-4))) f(0. 25)=3. 896875 Galat yang terjadi 0. 625

Hilangnya angka signifikan o o Hilangnya angka signifikan terjadi jika dua buah bilangan yang hampir sama dibandingkan. Hilangnya angka signifikan sering berakibat fatal bagi perhitungan numerik Contoh. 13 = 13. 0000 6 a. s 0. 0385 3 a. s

Deret Taylor & Deret Mac. Laurin n Deret Taylor di titik a n Jika a = 0 maka akan menjadi deret Mac. Laurin

Contoh. ¡ ¡ f(x) = sin x l f’(x) = cos x l f’’(x) = - sin x l f’’’(x) = -cos x l Dst…. Deret Mac. Laurin

• Deret Taylor dan deret Mac. Laurin dapat digunakan dalam perhitungan untuk mencegah hilangnya angka signifikan • Contoh. • Untuk x = 0. 5 maka sin 0. 5 – 0. 5 = 0. 02057 (4 a. s) • Diperoleh 0. 02031 (4 a. s)

l Fungsi Pendekatan

Pendahuluan Masalah yang sulit dievaluasi Fungsi yang “rumit” ¨ Fungsi pendekatan dengan menyederhanakan fungsi Informasi tentang fungsi dalam bentuk tabel nilai (hanya sebagian informasi yang diketahui) Fungsi pendekatan dengan pendekatan nilai dari data Digunakan fungsi pendekatan berupa polinomial yang memenuhi fungsi pada sejumlah titik

n n n Misalkan nilai fi = f(xi) diketahui i = 1, 2, 3, …, n Dapat digunakan fungsi polinomial pn(x) dengan derajat ≤ n untuk menginterpolasi fungsi di (n + 1) titik xi, i = 1, 2, 3, …, n Polinomial interpolasi yang digunakan harus memenuhi

Bentuk Lagrange l Didefinisikan fungsi

• Jika fi adalah nilai fungsi di titik xi maka jumlah dari perkalian fi dengan Li(x) adalah pn(x) = f 1 L 1(x) + f 2 L 2(x) + … + fn. Ln(x) Bentuk di atas disebut bentuk Lagrange polinomial interpolasi

Contoh. ¡ Tentukan polinomial untuk menginterpolasi fungsi di titik x = -1, 0 dan 1 ¡ Jawab. Misal x 0 = -1, x 1 = 0 dan x 2 = 1 ¡

l Diperoleh polinomial interpolasi p 2(x)=f 0 L 0(x)+f 1 L 1(x)+f 2 L 2(x) = =

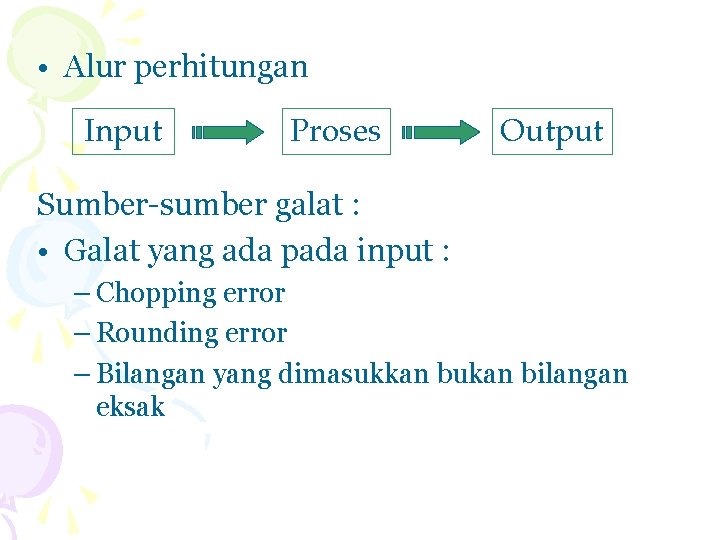
Formula Pembagian Selisih Newton xi f(xi) f[xi, xi+1] f[xi, xi+1, xi+2]

n Dari langkah-langkah di atas diperoleh polinomial interpolasi pn(x) = f(x 0)+(x - x 0)f[x 0, x 1]+(x - x 0)(x-x 1)f[x 0, x 1, x 2]+…+ (x - x 0)…(x - xn-1)f[x 0, x 1, …, xn] n Contoh. Gunakan formula pembagian selisih Newton untuk menginterpolasi di titik x = 2, 3, 4 dan 6

Jawab. xi f(xi) 2 1. 414214 0. 317837 3 1. 732051 -0. 024944 0. 002636 0. 267949 4 2. 000000 -0. 014401 0. 224745 n 6 2. 449490 Polinomial interpolasi pn(x) = 1. 414214 + (x – 2){0. 317837 + (x – 3){-0. 024944 + (x – 4)(0. 002636)}}

Galat dari polinomial interpolasi n n n Misal polinom pn(x) dengan derajat ≤ n yang menginterpolasi fungsi f di xi [a, b], i = 0, 1, 2…, n Jika derivatif fungsi ke - n+1 kontinu pada [a, b] maka galat Dengan x berada dalam interval yang memuat x, x 0, x 1, … , xn

Contoh. n n Tentukan error di titik x = 5 dari polinomial interpolasi di titik x = 2, 3, 4 dan 6 Jawab.

PERSAMAAN NONLINIER

Persamaan nonlinier n Pada umumnya persamaan nonlinier f(x) = 0 tidak dapat mempunyai solusi eksak n Jika r suatu bilangan real sehingga f(r) = 0 maka r disebut sebagai akar dari persamaan nonlinier f(x) n Solusi dari persamaan nonlinier dapat ditentukan dengan menggunakan metode iterasi

• Persamaan nonlinier f(x) = 0 – Tidak mempunyai akar – Mempunyai beberapa akar – Mempunyai banyak akar • Metode pencarian akar dari persamaan nonlinier – Metode biseksi (Bisection Method) – Iterasi titik tetap (Fixed Point Iteration) – Metode Newton (Newton Method)

Metode biseksi Jika f(x) kontinu pada interval [a, b] dan f(a). f(b) < 0 maka terdapat minimal satu akar. Algoritma sederhana metode biseksi 1. Mulai dengan interval [a, b] dan toleransi 2. Hitung f(b) 3. Hitung c = (a - b)/2 dan f(c) 4. Jika b – c ≤ maka STOP ( akar = c) 5. Jika f(b). f(c) < 0 maka a = c jika tidak b = c dan f(b) = f(c) 6. Ulangi langkah 3

Contoh. Gunakan metode biseksi untuk mencari akar dari x – 1 = e-x pada interval [1, 1. 4] dengan toleransi = 0. 02 ¡ Jawab. ¡

a b c f(b) f(c) f(b). f(c) action error 1 1. 4 1. 2 0. 15 -0. 1 <0 a=c 0. 2 1. 4 1. 3 0. 15 0. 027 >0 b=c 0. 1 1. 2 1. 3 1. 25 0. 027 -0. 037 <0 a=c 0. 05 1. 25 1. 3 1. 275 0. 027 -0. 0044 <0 a=c 0. 025 1. 275 1. 3 1. 2875 n. Diperoleh akarnya adalah x 1. 2875 0. 0125

Kekonvergenan metode biseksi n Menentukan banyaknya iterasi sehingga error maksimumnya ≤ Iterasi Lebar interval 0 B–a 1 (b – a)/2 2 (b – a)/4 . . n (b – a)/2 n

l Error maksimum l Banyaknya iterasi

Contoh. n n Berapa iterasi yang diperlukan agar error maksimum pada metode biseksi lebih kecil dari 10 -5 pada interval [0, 1]? Jawab.

Iterasi titik tetap Misal terdapat fungsi f(x) = 0 Ditentukan fungsi baru dengan bentuk x = g(x) Kemungkinan dari penentuan fungsi x = g(x) q q Konvergen Digunakan untuk melakukan iterasi dengan inisialisasi x 0 f(r) = 0 ↔ r = g(r) dan r disebut titik tetap

Contoh. ¢ ¢ Tentukan akar hampiran dari fungsi x 3 – 2 x + 1 = 0 dengan x 0 = 2 Jawab. Ditentukan fungsi baru 2 x = x 3 + 1 x = ½ (x 3 + 1) xn+1 = ½ (xn 3 + 1) dengan x 0 = 2 Dari tabel terlihat bahwa penentuan fungsi x = g(x) bersifat divergen Iterasi xn xn+1 0 2 4. 5 1 4. 5 46… 2 46….

n n Penentuan fungsi baru yang lain x 3 – 2 x + 1 = 0 Iterasi xn xn+1 0 2 1. 4422 1. 225 1. 137 Setelah 3 iterasi diperoleh akar hampiran x = 1. 137

Metode Newton o o Dalam metode ini, fungsi y = f(x) dianggap sebagai garis lurus yang melalui titik (a, f(a)), menyinggung kurva y = f(x) dan memotong sumbu X di titik (x, 0) Gradien kurva m = f’(a)

Menyinggung kurva f = f(x) persamaan garis singgungnya adalah y – f(a) = m (x – a) y – f(a) = f’(a)(x – a) Karena memotong sumbu X di (x, 0) maka 0 – f(a) = f’(a)(x – a)

n Iterasi metode Newton n Algoritma Newton Inisialisasi x = x 0, f’(x 0) 0 2. Hitung 1. |f(xn+1)| STOP (xn+1 akar hampiran) 4. Ulangi langkah 2 3.

Contoh. n n n Tentukan akar hampiran dari f(x) = x 2 – 2 x – 8 dengan x 0 = 3 Jawab. Iterasi x f(x) f’(x) = 2 x - 2 0 3 -5 4 1 4. 25 1. 5625 6. 5 2 4. 009 0. 054 6. 018 3 4. 00 Setelah iterasi ke-3 diperoleh akar = 4. 00

PERSAMAAN DIFERENSIAL BIASA

Pengantar n n n Misalkan terdapat masalah nilai awal (initial value problem/IVP) y’ = f(x, y) dengan y(a) = Secara umum, masalah di atas dapat diselesaikan secara numerik Contoh. y’ = y dengan y(0) = 2

Penyelesaian persamaan diferensial biasa Diketahui IVP y’ = f(x, y) dengan y(a) = Misalkan penyelesaian IVP di atas pada interval [a. b], ambil titik dengan jarak yang sama xn = a + nh , n = 0, 1, 2, …, N dengan h = (b – a)/N Untuk menentukan penyelesaian dari persamaan diferensial biasa dapat dilakukan dengan : Metode Euler Metode Taylor Metode Runge Kutta

Metode Euler l l Merupakan metode yang paling sederhana dalam menyelesaikan IVP Diferensial tingkat pertama sebagai kemiringan (slope) dari kurva fungsi

l Dalam menentukan penyelesaian dilakukan dengan iterasi xn = a + nh

Contoh. ¡ ¡ ¡ Tentukan penyelesaian dari di x = 2 dengan h = 0. 5 Jawab. Diketahui x 0 = 1 dan y 0 = 4 berada di interval [1, 2] dengan h = 0. 5 diperoleh N = 2 (yang berarti ada 2 iterasi)

n Untuk iterasi awal n = 0

¢ Iterasi kedua ¢ Di titik x = 2 diperoleh y(2) = 5. 403509

Metode Taylor n Perhatikan deret Taylor di titik x = a berikut. n Dari deret Taylor di atas dapat digunakan untuk menghitung IVP. Metode Taylor orde 2

Contoh. o Gunakan metode Taylor orde 2 untuk menghitung nilai y(2) dengan h = 0. 5 dari o Jawab.

• Dari soal diketahui h = 0. 5, x 0= 1 dan y 0= 4

Di titik x = 2 diperoleh y(2) = 5. 468272

Metode Runge Kutta n Pada metode ini, tidak perlu evaluasi derivatif orde tinggi Bentuk umum n Atau n Dengan

Contoh. n n n Gunakan metode Runge Kutta untuk menghitung nilai y(2) dengan h = 0. 5 dari Jawab. Dari soal diketahui h = 0. 5, x 0= 1 dan y 0= 4 Iterasi awal n = 0

n Iterasi kedua n = 1

Di titik x = 2 diperoleh y(2) = 5. 464395