Metode Linier Programming Metode Simpleks Pengantar 1 Metode

Metode Linier Programming Metode Simpleks

Pengantar (1) • Metode Simpleks merupakan prosedur aljabar yang bersifat iteratif, yang bergerak selangkah demi selangkah dimulai dari titik ekstrim pada daerah fisibel hingga titik ekstrim yang optimum • Syarat suatu kasus dapat diselesaikan dengan metode simpleks : ü Variabel keputusan ≥ 2 ü Jumlah fungsi pembatas ≥ 1 ü Jenis tanda pada fungsi pembatas bertanda ≤

Pengantar (2) • Beberapa istilah dalam metode simpleks : Basis variabel (BV), adalah semua variabel pada fungsi tujuan yang berharga positif dan bukan nol Non basis variabel (NBV), adalah semua variabel pada fungsi tujuan yang berharga bukan positif dan nol Entering variabel (EV), adalah variabel non basis yang berubah menjadi variabel basis Leaving variabel (LV), adalah variabel basis yang berubah menjadi variabel non basis Variabel Slack (S), variabel yang ditambahkan pada pertidaksamaan fungsi pembatas sehingga menjadi persamaan

Algoritma Simpleks (1) • Formulasikan permasalahan menjadi model Linier Programming (LP) standar • Ubah model LP standar menjadi model kanonik dengan menambahkan variabel slack pada fungsi pembatas • Tentukan basis dan non basis variabel • Masukkan semua nilai koefesien masing-masing variabel pada tabel simpleks iterasi 0 • Tentukan entering variabel (EV) • Tentukan rasio perbandingan antara kolom rhs (right hand side) dengan kolom EV • Tentukan leaving variabel (LV)

Algoritma Simpleks (2) • Lakukan proses iterasi simpleks hingga didapatkan hasil optimal sesuai dengan jenis fungsi tujuan (maksimasi atau minimasi ) • Aturan berhenti : Untuk fungsi tujuan maksimasi, iterasi dikatakan optimal jika seluruh koefesien fungsi variabel sudah bernilai positif atau nol Untuk fungsi tujuan minimasi, iterasi dikatakan optimal jika seluruh koefesien fungsi variabel sudah bernilai negatif atau nol

Entering Variabel (EV) • Untuk fungsi tujuan maksimasi, EV ditentukan dari nilai variabel pada fungsi tujuan yang paling kecil dan bukan nol • Untuk fungsi tujuan minimasi, EV ditentukan dari nilai variabel pada fungsi tujuan yang paling besar dan bukan nol

Leaving Variabel (LV) • Untuk fungsi tujuan maksimasi & minimasi, LV ditentukan dari nilai rasio yang paling kecil dan bukan berharga negatif

Contoh : Maks Z = 60 X 1 + 30 X 2 + 20 X 3 s/t 8 X 1 + 6 X 2 + X 3 ≤ 48 4 X 1 + 2 X 2 + 3/2 X 3 ≤ 20 2 X 1 + 3/2 X 2 + 1/2 X 3 ≤ 8 X 2 ≤ 5 X 1 , X 2 , X 3 ≥ 0

Ubah ke bentuk kanonik Maks Z = 60 X 1 + 30 X 2 + 20 X 3 s/t 8 X 1 + 6 X 2 + X 3 + S 1 = 48 4 X 1 + 2 X 2 + 3/2 X 3 + S 2 = 20 2 X 1 + 3/2 X 2 + 1/2 X 3 + S 3 = 8 X 2 + S 4 =5 X 1 , X 2 , X 3, S 1, S 2, S 3, S 4 ≥ 0

Basis dan non basis variabel • Jika pada persamaan kanonik kita misalkan nilai X 1 , X 2 dan X 3 = 0, maka nilai S 1, S 2, S 3. S 4 tidak sama dengan nol • Maka BV : Z, S 1, S 2, S 3, S 4 NBV : X 1, X 2, X 3

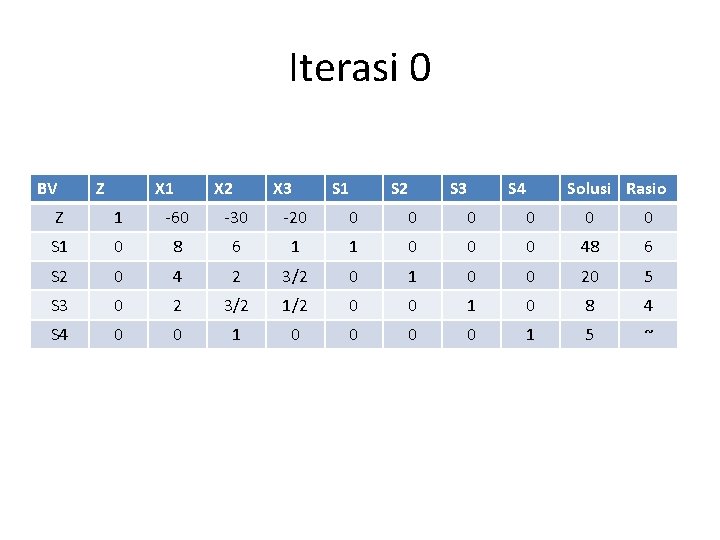
Iterasi 0 BV Z X 1 X 2 X 3 S 1 S 2 S 3 S 4 Solusi Rasio Z 1 -60 -30 -20 0 0 0 S 1 0 8 6 1 1 0 0 0 48 6 S 2 0 4 2 3/2 0 1 0 0 20 5 S 3 0 2 3/2 1/2 0 0 1 0 8 4 S 4 0 0 1 5 ~

Rumusan iterasi Nilai baru = nilai awal + (PV x PR) PV = PIVOT POIN PR = PIVOT ROW

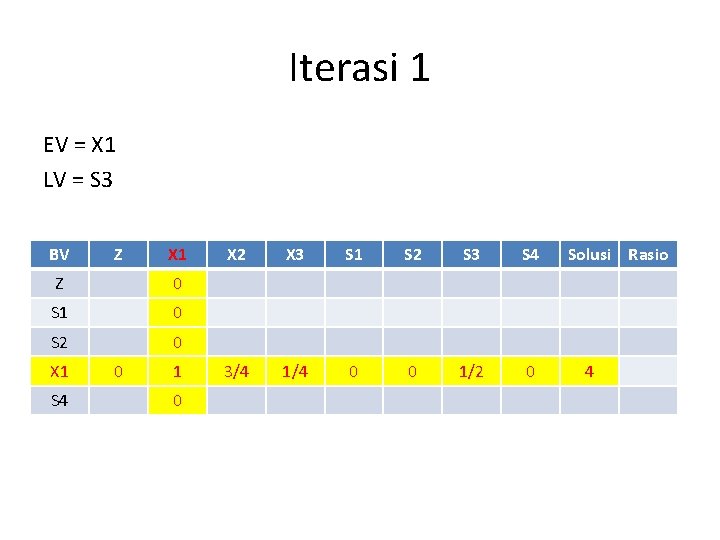
Iterasi 1 EV = X 1 LV = S 3 BV Z X 1 Z 0 S 1 0 S 2 0 X 1 S 4 0 1 0 X 2 X 3 S 1 S 2 S 3 S 4 3/4 1/4 0 0 1/2 0 Solusi Rasio 4

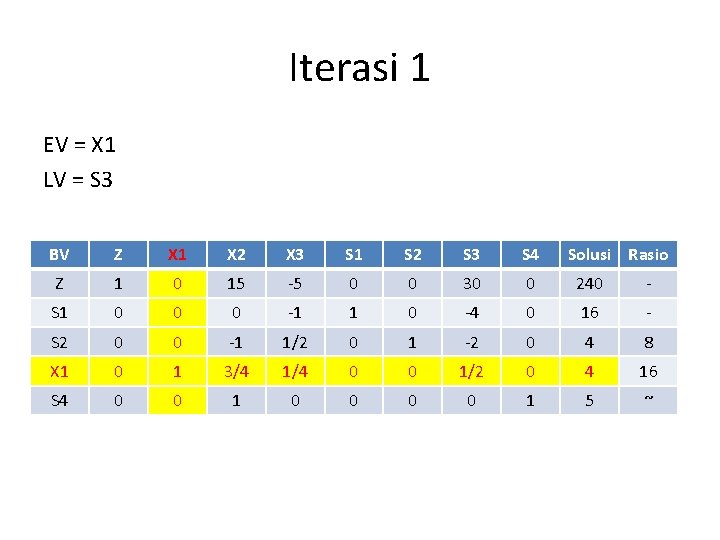
Iterasi 1 EV = X 1 LV = S 3 BV Z X 1 X 2 X 3 S 1 S 2 S 3 S 4 Solusi Rasio Z 1 0 15 -5 0 0 30 0 240 - S 1 0 0 0 -1 1 0 -4 0 16 - S 2 0 0 -1 1/2 0 1 -2 0 4 8 X 1 0 1 3/4 1/4 0 0 1/2 0 4 16 S 4 0 0 1 5 ~

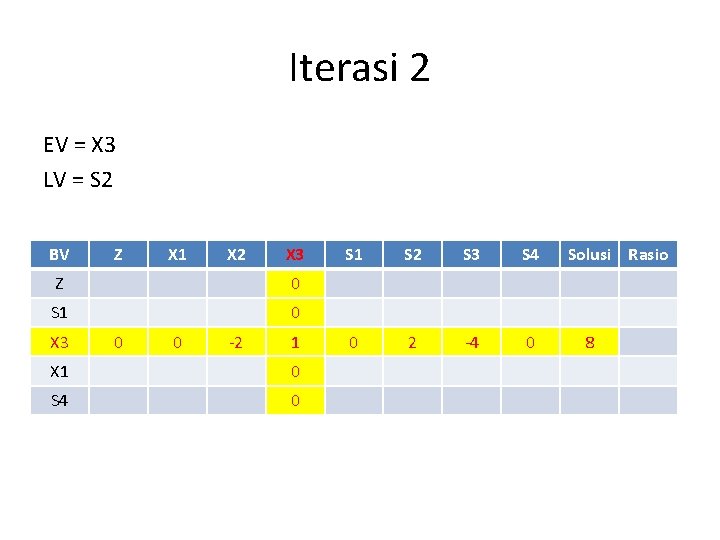
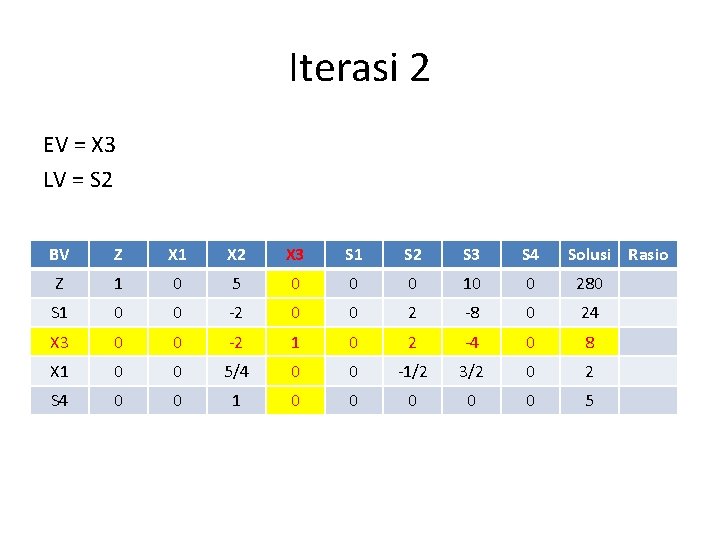
Iterasi 2 EV = X 3 LV = S 2 BV Z X 1 X 2 X 3 Z 0 S 1 0 X 3 0 0 -2 1 X 1 0 S 4 0 S 1 S 2 S 3 S 4 0 2 -4 0 Solusi Rasio 8

Iterasi 2 EV = X 3 LV = S 2 BV Z X 1 X 2 X 3 S 1 S 2 S 3 S 4 Solusi Rasio Z 1 0 5 0 0 0 10 0 280 S 1 0 0 -2 0 0 2 -8 0 24 X 3 0 0 -2 1 0 2 -4 0 8 X 1 0 0 5/4 0 0 -1/2 3/2 0 2 S 4 0 0 1 0 0 0 5

Solusi optimal X 1 = 2 X 2 = 0 X 3 = 8 Z = 280

Latihan Soal : Min Z = 3 X 1 - 5 X 2 s/t X 1 ≤ 4 2 X 2 ≤ 12 3 X 1 + 2 X 2 ≤ 18 X 1 , X 2 ≥ 0

Solusi (1) Iterasi 0 BV Z XI X 2 S 1 S 2 S 3 Solusi Rasio Z S 1 S 2 S 3 Iterasi 1 BV Z

Solusi (2) Iterasi 2 BV Z XI X 2 S 1 S 2 S 3 Solusi Rasio

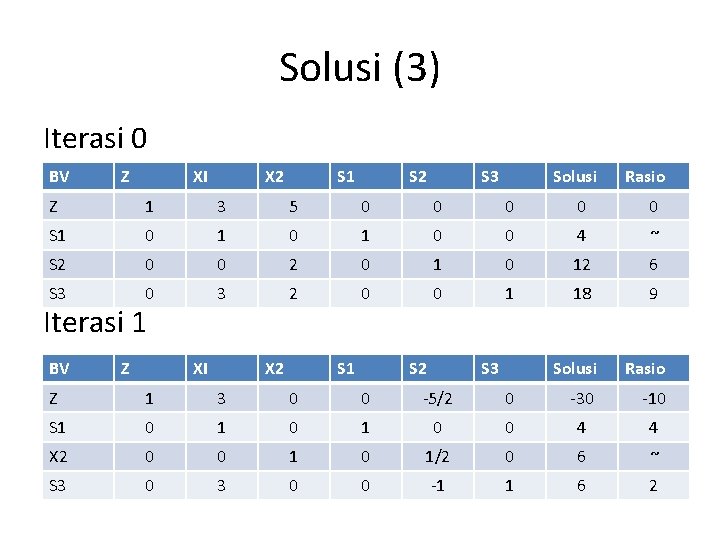
Solusi (3) Iterasi 0 BV Z XI X 2 S 1 S 2 S 3 Solusi Rasio Z 1 3 5 0 0 0 S 1 0 1 0 0 4 ~ S 2 0 0 2 0 12 6 S 3 0 3 2 0 0 1 18 9 Iterasi 1 BV Z XI X 2 S 1 S 2 S 3 Solusi Rasio Z 1 3 0 0 -5/2 0 -30 -10 S 1 0 1 0 0 4 4 X 2 0 0 1/2 0 6 ~ S 3 0 0 -1 1 6 2

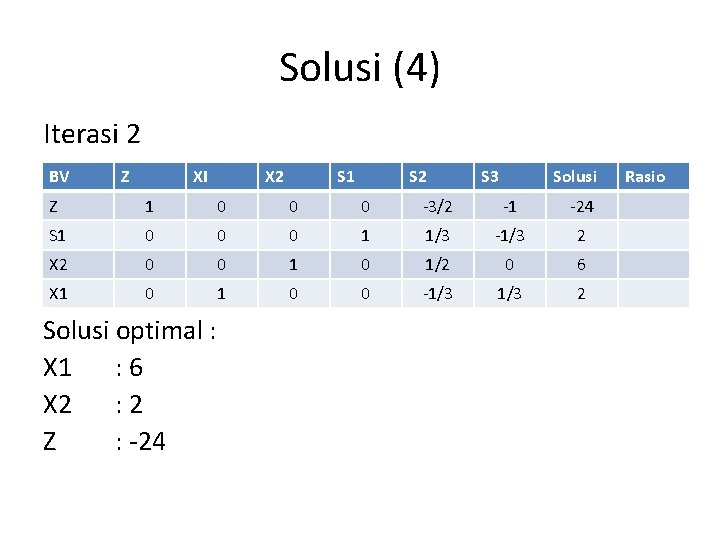
Solusi (4) Iterasi 2 BV Z XI X 2 S 1 S 2 S 3 Solusi Z 1 0 0 0 -3/2 -1 -24 S 1 0 0 0 1 1/3 -1/3 2 X 2 0 0 1/2 0 6 X 1 0 0 -1/3 2 Solusi optimal : X 1 : 6 X 2 : 2 Z : -24 Rasio