DIFFERENSIASI NUMERIK Yuliana Setiowati DIFFERENSIASI NUMERIK n n

DIFFERENSIASI NUMERIK Yuliana Setiowati

DIFFERENSIASI NUMERIK n n Salah satu perhitungan kalkulus yang banyak digunakan adalah differensial Differensial digunakan untuk keperluan perhitungan geometrik, yang berhubungan dengan perubahan nilai per-satuan waktu atau jarak. Secara kalkulus, didefinisikan sebagai perbandingan perubahan tinggi (selisih tinggi) dan perubahan jarak penentuan titik puncak kurva y = f(x) dy/dx = 0

Mengapa perlu Metode Numerik ? n n Terkadang terdapat suatu fungsi yang sulit dihitung secara manual Untuk mengotomatiskan, tanpa harus menghitung manualnya

DIFFERENSIASI NUMERIK n Hubungan antara nilai fungsi dan perubahan fungsi untuk setiap titiknya didefinisikan : n y = f(X) + f 1(x). h(x)

Diferensiasi dg Met. Num n n n Metode Selisih Maju Metode Selisih Tengahan Metode Selisih Mundur

Metode Selisih Maju n n n Metode selisih maju merupakan metode yang mengadopsi secara langsung definisi differensial Pengambilan h diharapkan pada nilai yang kecil agar errornya kecil Error yang dihasilkan

Contoh : n n n Hitung differensial f(x)=e-xsin(2 x) +1 dari range x=[0, 1] dengan h=0. 05

Metode Selisih Tengahan n Metode selisih tengahan merupakan metode pengambilan perubahan dari dua titik sekitar dari titik yang diukur. Perhatikan selisih maju pada titik x-h n selisih maju pada titik x n n Metode selisih tengahan merupakan rata-rata dari dua selisih maju :

Metode Selisih Tengahan n Kesalahan pada metode ini

Metode Selisih Mundur

Contoh n Hitung differensial f(x)=e-xsin(2 x)+1 dari range x=[0, 1] dengan h=0. 05

Differensiasi tingkat tinggi n Differensiasi tingkat tinggi merupakan proses pendifferensialan secara terus-menerus, hingga tingkatan yang ditentukan. Differensial tingkat 2 n Differensial tingkat 3 n Differensial tingkat n n

Differensiasi tingkat tinggi n Differensiasi tingkat 2 untuk M. Selisih Maju

Differensiasi tingkat tinggi n Differensiasi tingkat 2 untuk M. Selisih Tengahan

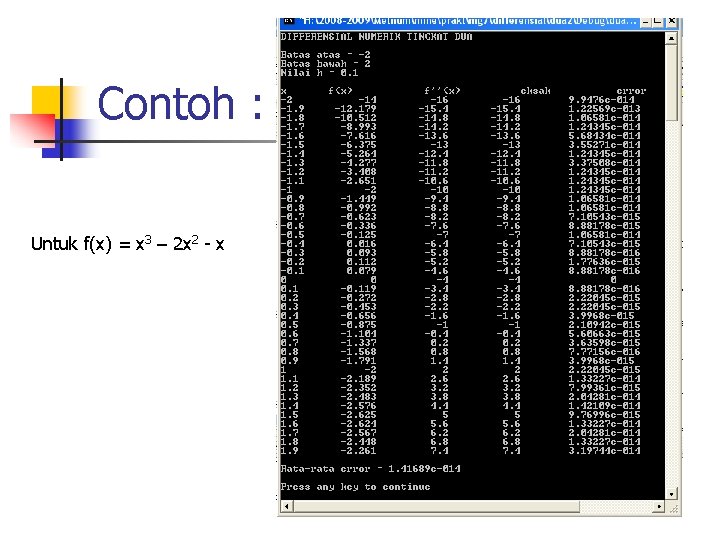
Contoh : Untuk f(x) = x 3 – 2 x 2 - x

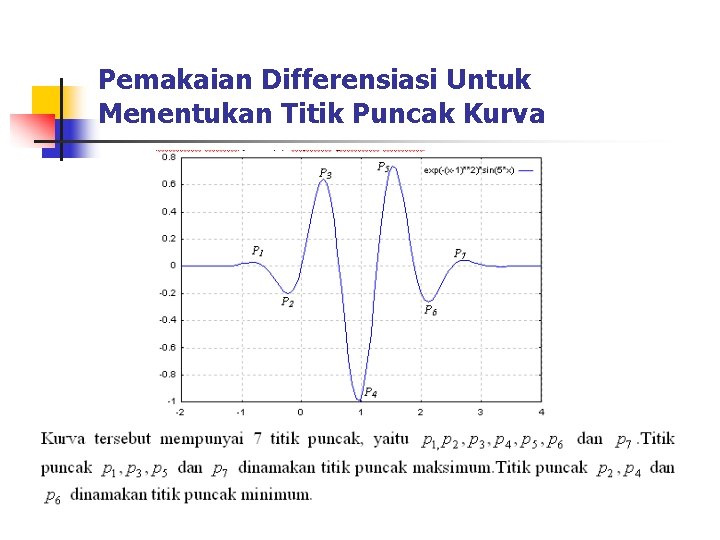
Pemakaian Differensiasi Untuk Menentukan Titik Puncak Kurva

Pemakaian Differensiasi Untuk Menentukan Titik Puncak Kurva n n n Definisi 5. 1. Suatu titik a pada kurva y = f(x) dinamakan titik puncak bila dan hanya bila : f 1(a) = 0. Definisi 5. 2. Sebuah titik puncak a dikatakan titik maksimum pada kurva y = f(x) bila : f 11(a) < 0. Definisi 5. 3. Sebuah titik puncak a dikatakan titik minimum pada kurva y = F(x) bila : f 11(a) > 0.

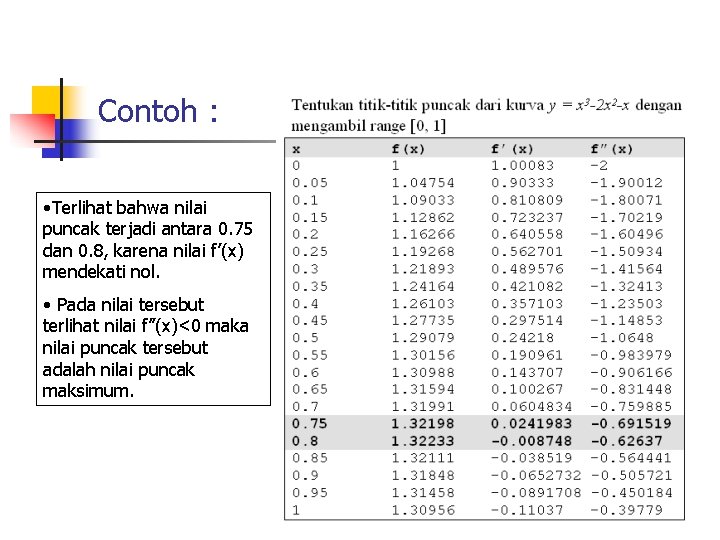
Contoh : • Terlihat bahwa nilai puncak terjadi antara 0. 75 dan 0. 8, karena nilai f’(x) mendekati nol. • Pada nilai tersebut terlihat nilai f”(x)<0 maka nilai puncak tersebut adalah nilai puncak maksimum.