INTEGRASI NUMERIK 1 METODE PERSEGI PANJANG n Metode

INTEGRASI NUMERIK 1

METODE PERSEGI PANJANG n Metode secara numerik A. Metode Pendekatan Persegi Panjang B. Metode Trapesium A. Metode Pendekatan Persegi Panjang § § Bagi interval a sampai b atas n sub-interval Hitung nilai fungsi pada ujung-ujung sub-interval tersebut f (xk ) Hitung luas tiap-tiap persegi panjang tersebut Pk = h * f (xk ) Jumlahkan semua luas persegi panjang tersebut 2

METODE PERSEGI PANJANG n n Selain mengambil tinggi persegi panjang ke-k, sama dengan f (xk ) yaitu nilai fungsi pada ujung kanan sub-interval ke-k tersebut, juga dapat mengambil tinggi sama dengan f (xk-1 ) yaitu nilai fungsi pada ujung kiri sub-interval, ataupun juga pada : yaitu nilai fungsi pada titik tengah sub-interval Contoh: Cari luas daerah di bawah kurva f(x) = x 2, antara x = 0 sampai x = 4 Solusi: Ø Interval (0, 4) dibagi menjadi 4 bagian sama panjang, n = 4 h = (4 - 0)/4 = 1 Ø Luas persegi panjang P 1 = 1 * f(1) = 1 * 1 =1 P 2 = 1 * f(2) = 1 * 4 = 4 P 3 = 1 * f(3) = 1 * 9 = 9 + P 4 = 1 * f(4) = 1 * 16 = 16 Luas Total = 30 Penyimpangannya = 30 – 21. 33 = 8. 66 3

METODE PERSEGI PANJANG Ø Ø P 3 P 4 P 6 P 7 P 8 Jika interval (0, 4) dibagi menjadi 8 sub-interval, n = 8 h = (4 - 0)/8 = 0. 5 Luas persegi panjang P 1 = 1 * f(0. 5) = 1 * 1 = 0. 125 P 2 = 1 * f(1. 0) = 1 * 4 = 1 * f(1. 5) = 1 * 9 = 1. 125 = 1 * f(2. 0) = 1 * 16 = 2 P 5 = 1 * f(2. 5) = 1 * 4 = 3. 125 = 1 * f(3. 0) = 1 * 9 = 4. 5 + = 1 * f(3. 5) = 1 * 16 = 6. 125 = 1 * f(4. 0) = 1 * 16 = 8 Luas Total = 26 Penyimpangannya = 26 – 21. 33 = 4. 67 Ø Jika banyaknya sub-interval diperbanyak lagi, misal n = 40, diperoleh L = 22. 14, dan untuk n = 100 diperoleh L = 21. 6544 4

METODE PERSEGI PANJANG Ø Jika diambil tinggi adalah nilai fungsi pada ujung kiri sub-interval Luas P 1 = 0. 5 * f(0. 0) = 0. 5 * 0 =0 P 2 = 0. 5 * f(0. 5) = 0. 5 * 0. 25 = 0. 125 P 3 = 0. 5 * f(1. 0) = 0. 5 * 1 =1 P 4 = 0. 5 * f(1. 5) = 0. 5 * 2. 25 = 1. 125 P 5 = 0. 5 * f(2. 0) = 0. 5 * 4 =2 P 6 = 0. 5 * f(2. 5) = 0. 5 * 6. 25 = 3. 125 + P 7 = 0. 5 * f(3. 0) = 0. 5 * 9 = 4. 5 P 8 = 0. 5 * f(3. 5) = 0. 5 * 12. 25 = 6. 125 Luas Total = 18 5

METODE PERSEGI PANJANG Ø Jika tinggi sama dengan titik tengah interval, diperoleh: Luas P 1 = 0. 5 * f(0. 25) = 0. 03125 P 2 = 0. 5 * f(0. 75) = 0. 28125 P 3 = 0. 5 * f(1. 25) = 0. 78125 P 4 = 0. 5 * f(1. 75) = 1. 53125 P 5 = 0. 5 * f(2. 25) = 2. 53125 P 6 = 0. 5 * f(2. 75) = 3. 78125 + P 7 = 0. 5 * f(3. 25) = 5. 23125 P 8 = 0. 5 * f(3. 75) = 7. 03125 Luas Total = 21. 2000 Perhatikan bahwa hasil terakhir ini adalah yang terbaik. 6

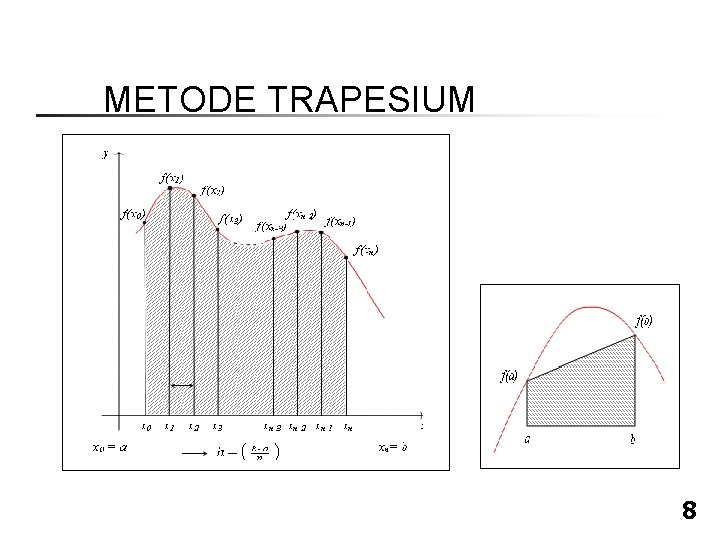
METODE TRAPESIUM B. Metode Trapesium § § § Bagi interval (a, b) menjadi n sub-interval yang sama Hitung nilai fungsi pada ujung-ujung sub-interval tersebut f (xk ) Hitung luas trapesium Pk = h * f (xk ) Luas trapesium ke-1 = t 1 = ½ ( f(x 0) + f(x 1) ) * h = h/2 ( f(x 0) + f(x 1) ) ke-2 = t 2 = ½ ( f(x 1) + f(x 2) ) * h = h/2 ( f(x 1) + f(x 2) ) ……………. ke-n = tn = ½ ( f(xn-1) + f(xn) ) * h = h/2 (f(xn-1) + f(xn) ) Luas Total = t 1 + t 2 + ……. + tn = h/2 ( f(x 0) + f(x 1) ) + h/2 ( f(x 1) + f(x 2) ) + ……. + h/2 (f(xn-1) + f(xn) ) 7

METODE TRAPESIUM 8

METODE TRAPESIUM n Contoh: Hitung luas daerah di bawah kurva f(x) = x 2, antara x = 0 sampai x = 4 Solusi: Ø Interval (0, 4) dibagi menjadi 4 sub-interval, n = 4 h = (4 - 0)/4 = 1 Ø xk 0 1 2 3 4 f(xk) 0 1 4 9 16 Luas total 9

METODE KUADRATUR GAUSS n n n Rumusan yang paling akurat untuk integrasi numerik Tinjauan Gauss dalam perhitungan integral F(x) dx berdasarkan nilai f(x) dalam sub interval yang tidak berjarak sama, melainkan simetris terhadap titik tengah interval I= f(x) dx = (a-b) [R 1 (U 1 ) + R 2 (u 2) + … + Rn (Un)] U 1, U 2, …, Un adalah titik dalam interval [-1/2, 1/2] (U) = f(x) = f[(b-a)u + ] X = (b-a)u + (Tersedia tabel nilai numerik parameter U dan R) 10

ALGORITMA KUADRATUR GAUSS Algoritma: a) b) c) d) e) f) g) Inisialisasi tabel koefisien gauss Definisikan fungsi integran Tentukan batas pengintegralan a dan b Inisialisasi : sum = 0 Hitung : sum = sum + Ri x (Ui), i = 1 sampai n Hitung : I = (b-a) x sum Tulis hasil integral 11

METODE SIMPSON n n n Paling luas pemakaiannya Untuk pendekatannya memakai parabola yang melalui 3 ordinat dari 2 interval berdampingan Eksak untuk polinim derajat dua atau kurang Lebih teliti dan rumus tidak lebih rumit dari metode trapesium n = banyak interval h= I= + (Y 0 + 4 Y 1 + 2 Y 2 + 4 Y 3 + 2 Y 4 +…+ 2 Yn-4 + 4 Yn-3 + 2 Yn-2 4 Yn-1 + Yn) Kesalahan pemotongan : e. T ~ (b-a) f (Q), a<Q<b 12

ALGORITMA METODE SIMPSON Algoritma: a) b) c) d) e) f) g) Definisikan fungsi integran Tentukan batas pengintegralan a dan b dan jumlah segmen n (harus genap) Hitung : h = (b-a)/n Inisialisasi sum = F (a) + 4 x F (a+h) Hitung untuk i = 2 sampai i = n-1 dengan indeks pertambahan sama dengan 2 sum = sum + 2 x F (a+ixh) + 4 x F (a+(i+1)h) Hitung nilai integral I = h/3 x (sum + F(b)) Tulis hasil perhitungan 13