Matrices y Determinantes Concepto de matriz Igualdad de

Matrices y Determinantes

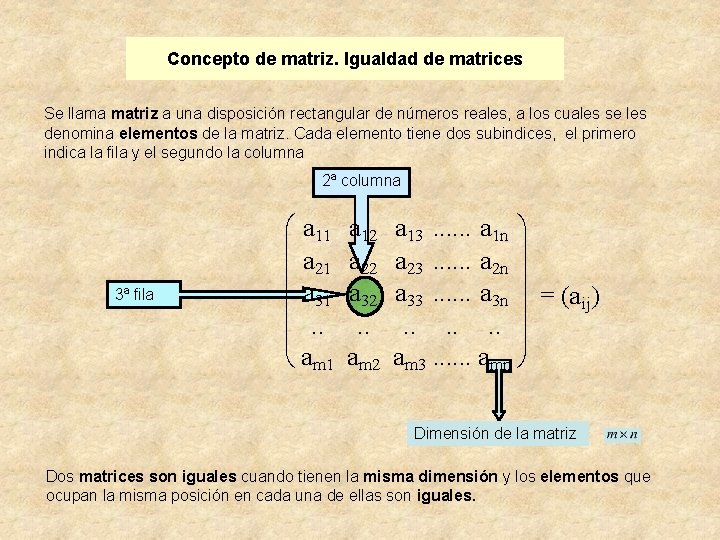
Concepto de matriz. Igualdad de matrices Se llama matriz a una disposición rectangular de números reales, a los cuales se les denomina elementos de la matriz. Cada elemento tiene dos subindices, el primero indica la fila y el segundo la columna 2ª columna 3ª fila æ a 11 ç ç a 21 ç a 31 ç. . ç è am 1 a 12 a 22 a 32. . am 2 a 13. . . a 1 n ö ÷ a 23. . . a 2 n ÷ a 33. . . a 3 n ÷ = (aij). . . ÷÷ am 3. . . amn ø Dimensión de la matriz Dos matrices son iguales cuando tienen la misma dimensión y los elementos que ocupan la misma posición en cada una de ellas son iguales.

Definición de matríz Se llama matriz de orden m×n a todo conjunto rectangular de elementos aij dispuestos en m líneas horizontales (filas) y n verticales (columnas) de la forma: A = (ai, j)= Abreviadamente suele expresarse en la forma A =(aij), con i =1, 2, . . . , m, j =1, 2, . . . , n. Los subíndices indican la posición del elemento dentro de la matriz, el primero denota la fila ( i ) y el segundo la columna ( j ). Por ejemplo el elemento a 25 será el elemento de la fila 2 y columna 5. El orden es el número de filas y columnas que tiene la matriz, se representa por m x n.

Matriz: Ejemplo Juan, Ana y Elena han ido a una tienda y han comprado lo siguiente: 1. Juan compró dos bocadillos, un refresco y un pastel. 2. Ana se llevó un bocadillo, un refresco y un pastel. 3. Elena compró un bocadillo y un refresco. Estos datos se pueden agrupar en una matriz 2 1 1 1 1 0

Expresión matricial: ejemplo El sistema Tiene la siguiente matriz de los coeficientes: A = Tiene la siguiente matriz ampliada: A* Tiene la siguiente expresión matricial: æ ç ç è 2 5 – 3 ö÷ 1 – 4 1 ÷ø æ ç ç è 2 5 – 3 1 ö÷ = 1 – 4 1 – 2 ÷ ø æ ç ç è æ x ö æ 2 5 – 3 ç ÷ ç 1 y ÷ = çè – 2 1 – 4 1 ç è z ø ö ÷ ÷ ø

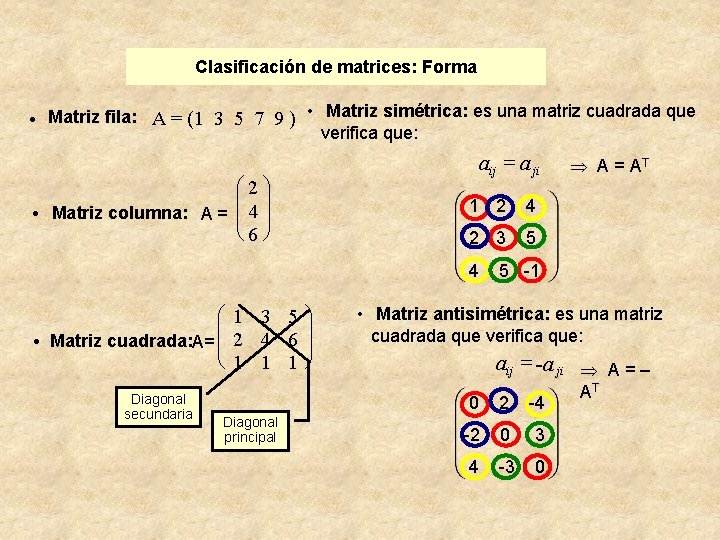
Clasificación de matrices: Forma · · Matriz fila: A = (1 3 5 7 9 ) • Matriz simétrica: es una matriz cuadrada que verifica que: aij = a ji æ 2ö ç ÷ Matriz columna: A = ç 4 ÷ è 6ø 1 2 4 2 3 5 4 · æ 1 3 5 ç Matriz cuadrada: A= ç 2 4 6 è 1 1 1 Diagonal secundaria Diagonal principal ö ÷ ÷ ø A = AT 5 -1 • Matriz antisimétrica: es una matriz cuadrada que verifica que: aij = -a ji A = – 0 2 -4 -2 0 3 4 -3 0 AT

Clasificación de matrices: Elementos • Matriz nula: es una matriz en la que todos los elementos son nulos. • Matriz unidad o identidad: es una matriz escalar, cuya diagonal principal es 1. • Matriz diagonal: es una matriz cuadrada, en la que todos los elementos no pertenecientes a la diagonal principal son nulos. • Matriz triangular superior: es una matriz donde todos los elementos por debajo de la diagonal son ceros. • Matriz escalar: es una matriz diagonal donde todos los elementos de ella son iguales. • Matriz triangular inferior: es una matriz donde todos los elementos por encima de la diagonal son ceros.

Operaciones con matrices Trasposición de matrices Suma y diferencia de matrices Producto de una matriz por un número Producto de matrices Propiedades simplificativas Matrices inversibles

Operaciones con matrices I 1. - Trasposición de matrices Dada una matriz de orden m x n, A = (aij), se llama matriz traspuesta de A, y se representa por At, a la matriz que se obtiene cambiando las filas por las columnas (o viceversa) en la matriz A. Es decir: Propiedades de la trasposición de matrices: 1ª. - Dada una matriz A, siempre existe su traspuesta y además es única. 2ª. - La traspuesta de la matriz traspuesta de A es A. a (At)t = A.

Matriz traspuesta: ejemplo y propiedades La traspuesta de una matriz A cualquiera se obtiene cambiando filas por columnas y se representa por At. Si A = (aij), entonces At = (aji). Si A es mxn, entonces At es nxm. Ejemplo: Si A æ ç =ç è æ 1 1 2 3 t ç entonces A = ç 2 4 5 6 è 3 ö ÷ ÷ ø 4 5 6 ö ÷ ÷ ø Propiedades: I. Para la matriz A, (At)t = A II. Para las matrices A y B, (A + B)t = At + Bt III. Para la matriz A y el número real k, (k. A)t = k. At IV. Para las matrices A y B, (A. B)t = Bt. At V. Si A es una matriz simétrica, At = A

Operaciones con matrices II 2. - Suma y diferencia de matrices La suma de dos matrices A=(aij), B=(bij) de la misma dimensión, es otra matriz S=(sij) de la misma dimensión que los sumandos y con término genérico S = (aij + bij). La suma de las matrices A y B se denota por A+B. Ejemplo Sin embargo, no se pueden sumar. Por tanto, para poder sumar dos matrices estas han de tener la misma dimensión. La diferencia de matrices A y B se representa por A–B, y se define como la suma de A con la opuesta de B : A–B = A + (–B)

Suma de matrices: ej de orden 3 Para sumar dos matrices A y B con las mismas dimensiones se suman los correspondientes elementos: si A = (aij) y B = (bij) entonces A + B = (aij + bij) æ a 11 a 12 a 13 a 14 ö æ b 11 b 12 b 13 b 14 ç ÷ ç A + B = (aij) + (bij) = ç a 21 a 22 a 23 a 24 ÷ + ç b 21 b 22 b 23 b 24 è a 31 a 32 a 33 a 34 ø è b 31 b 32 b 33 b 34 æ a 11 + b 11 ç a = ç 21 + b 21 è a 31 + b 31 a 12 + b 12 a 13 + b 13 a 14 + b 14 a 22 + b 22 a 23 + b 23 a 24 + b 24 a 32 + b 32 a 33 + b 33 a 34 + b 34 ö ÷ ÷ = ø ö ÷ ÷= (aij + bij ) ø

Propiedades de la adición de matrices Sean A, B y C tres matrices del mismo orden. • Asociativa: • Conmutativa: A + (B + C) = (A + B) + C A+B=B+A • Elemento neutro: A + 0 = 0 + A = A donde 0 es la matriz nula. • Elemento opuesto: A + (– A) = (– A) + A = 0 La matriz –A (opuesta) se obtiene cambiando de signo los elementos de A.

Operaciones con matrices III 3. - Producto de un número por una matriz Para multiplicar un número real por una matriz, se multiplican cada uno de los elementos de la matriz por dicho número. Si A = (aij), entonces k. A = (kaij) æ a 11 a 12 a 13 ö æ ka 11 ka 12 ka 13 ö ç ÷ ç a a a. . k A = k (aij) = k·ç 21 22 23 ÷ = ç ka 21 ka 22 ka 23 ÷÷ = (kaij) è a 31 a 32 a 33 ø è ka 31 ka 32 ka 33 ø

Propiedades con la suma y el producto por un número Sean A y B dos matrices del mismo orden y k y h dos números reales. • Distributiva I: k(A + B) = k. A + k. B • Distributiva II: (k + h)A = k. A + h. A • Elemento neutro: • Asociativa mixta: 1·A=A k(h. A) = (kh)A El conjunto de las matrices m x n con las operaciones suma y producto por un escalar antes definidas, tiene estructura de espacio vectorial

Operaciones con matrices IV 4. - Producto de matrices Dadas dos matrices A y B, su producto es otra matriz P cuyos elementos se obtienen multiplicando las filas de A por las columnas de B (por lo que deben coincidir estas). De manera más formal, los elementos de P son de la forma: Pij = a ik · bkj con k=1, …. n Es evidente que el número de columnas de A debe coincidir con el número de filas de B. Es más, si A tiene dimensión m x n y B dimensión n x p, la matriz P será de orden m x p, Ejemplos: no se pueden multiplicar

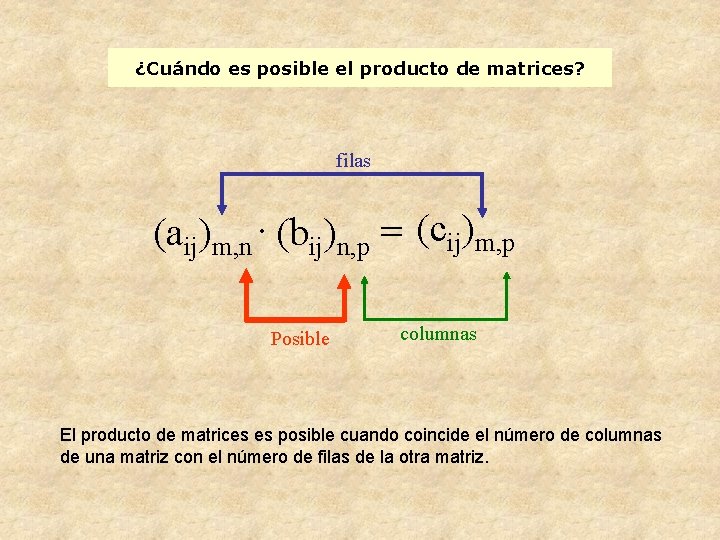
¿Cuándo es posible el producto de matrices? filas (aij)m, n. (bij)n, p = (cij)m, p Posible columnas El producto de matrices es posible cuando coincide el número de columnas de una matriz con el número de filas de la otra matriz.

Producto de matrices: Desarrollo El producto de la matriz A = (a ij) = por la matriz æ a 11 ça ç a 21 ç 31 ç. . è am 1 æ b 11 ç ç b 21 B = (b ij) = ç b 31 ç ç. . çb è n 1 a 12 a 22 a 32. . am 2 a 13. . . a 1 n ö a 23. . . a 2 n ÷ ÷ a 33. . . a 3 n ÷. . . ÷ am 3. . . amn ø b 12 b 13 . . . b 22 b 23 . . . b 32. . b 33. . . . bn 2 bn 3 . . . . b 1 p ö ÷ b 2 p ÷ b 3 p ÷ ÷. . ÷ b np ÷ø es la matriz C = A · B, tal que el elemento que ocupa la posición ij es: cij = ai 1. b 1 j + ai 2. b 2 j +. . . + ain. bnj

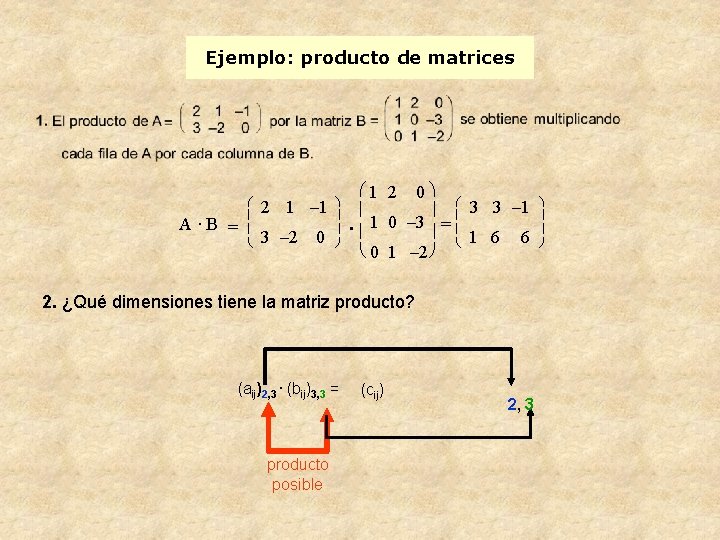
Ejemplo: producto de matrices A ·B = æ ç ç è 2 1 – 1 3 – 2 0 ö ÷ ÷ ø æ 1 2 0ö ç ÷ 1 0 – 3. ç ÷= è 0 1 – 2 ø æ ç ç è 3 3 – 1 1 6 6 2. ¿Qué dimensiones tiene la matriz producto? (aij)2, 3. (bij)3, 3 = producto posible (cij) 2, 3 ö ÷ ÷ ø

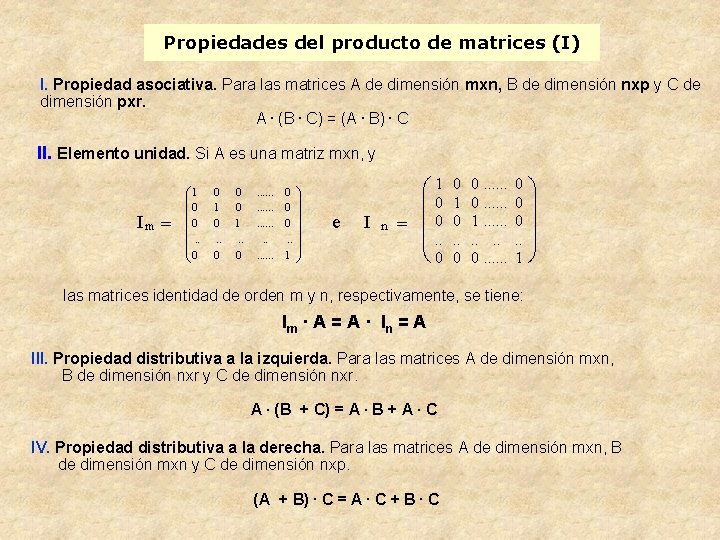
Propiedades del producto de matrices (I) I. Propiedad asociativa. Para las matrices A de dimensión mxn, B de dimensión nxp y C de dimensión pxr. A. (B. C) = (A. B). C II. Elemento unidad. Si A es una matriz mxn, y Im = æ 1 ç ç 0 ç ç. . ç è 0 0 1 0. . 0 0 0 1. . 0 . . . 0 0 0. . 1 ö ÷ ÷ ÷ ø e I n æ 1 ç 0 = ç 0 ç. . è 0 0 1 0. . 0 0 0 1. . 0 . . . 0 0 0. . 1 ö ÷ ÷ ÷ ø las matrices identidad de orden m y n, respectivamente, se tiene: Im · A = A · I n = A III. Propiedad distributiva a la izquierda. Para las matrices A de dimensión mxn, B de dimensión nxr y C de dimensión nxr. A. (B + C) = A. B + A. C IV. Propiedad distributiva a la derecha. Para las matrices A de dimensión mxn, B de dimensión mxn y C de dimensión nxp. (A + B). C = A. C + B. C

Propiedades del producto de matrices (II) I. La multiplicación de matrices no cumple la propiedad conmutativa: si una de las dos matrices no es cuadrada ni siquiera tiene sentido plantear el producto en un orden distinto al dado. II. Si A. B = 0 entonces no siempre ocurre que A = 0 ó B = 0. Ejemplo: Aunque æ ç ç è 0 2 ö÷. æç 0 – 3 ö÷ æç 0 0 ö÷ 0 0 ÷ø çè 0 0 ÷ø = çè 0 0 ÷ø ninguno de los factores que forman el producto es la matriz nula. III. Si A. C = B. C y C 0, entonces no necesariamente A = B. IV. (A + B)2 A 2 + 2 A. B + B 2 salvo que A y B conmuten. V. (A – B)2 A 2 – 2 A. B + B 2 salvo que A y B conmuten. VI. A 2 – B 2 (A – B). (A + B) salvo que A y B conmuten.

Producto: Potencia de una matriz Si A es una matriz cuadrada, las potencias de A, de exponente natural, se definen como en el caso de los números naturales: el exponente indica el número de veces que se multiplica la matriz por sí misma. n veces. A An = A. A. . . Ejemplo: æ 1 1ö ÷÷ = A çç è 0 1ø æ 1 1öæ 1 2 ö æ 1 3 ö ÷÷çç ÷÷ = çç ÷÷ A = A × A = çç è 0 1øè 0 1 ø 3 2 æ 1 1ö æ 1 2 ö ÷÷çç ÷÷ = çç ÷÷ A 2 = A × A = çç è 0 1ø è 0 1 ø æ 1 1ö æ 1 3 ö æ 1 4 ö 3 ÷÷ × çç ÷÷ = × × × = A A A A çç è 0 1ø è 0 1 ø 4 æ 1 1öæ 1 n - 1ö æ 1 n ö n-1 çç ÷÷ = × = An = A A L 3 1 2 1 ø è 0 1øè 0 n- veces

Operaciones con matrices V Inversa de una matriz, Matrices inversibles Una matriz cuadrada que posee inversa se dice que es inversible o regular; en caso contrario recibe el nombre de singular. Dada una matriz cuadrada A de orden n, no siempre existe otra matriz B tal que A·B = B·A = In. Si existe dicha matriz B, se dice que es la matriz inversa de A y se representa por A-1 Propiedades de la matriz inversa I. Si las matrices A y B son inversibles (A. B)– 1 = B– 1. A– 1 II. Si A es una matriz inversible y k 0, (k. A)– 1 = (1/k). A– 1 III. Si A es una matriz inversible, (A– 1)– 1 = A IV. La matriz unidad es inversible y además I– 1 = I V. Si A es una matriz inversible, (A– 1)t = (At)– 1

Métodos de cálculo de la matriz inversa Observación: Podemos encontrar matrices que cumplen A·B = I, pero que B·A ¹ I, en tal caso, podemos decir que A es la inversa de B "por la izquierda" o que B es la inversa de A "por la derecha". Hay varios métodos para calcular la matriz inversa de una matriz dada: ØDirectamente ØPor el método de Gauss-Jordan ØUsando determinantes

Inversa de una matriz (directamente) Si A es una matriz cuadrada, se dice que B es la inversa de A si A. B = B. A = I, siendo la matriz unidad. La matriz inversa se representa por A– 1. æ ç ç è æ ö 2 – 1 ö÷ ç x y ÷ -1 Ejemplo: Dada A = 1 1 ÷ø para obtener A = çè z t ÷ø se ha de cumplir æ ç ç è 2 – 1 ö÷ æç x y ö÷ æç 1 0 ö÷. 1 1 ÷ø çè z t ÷ø = çè 0 1 ÷ø Y de aquí se deduce que: æ ç ç è ö ÷ ÷ ø 2 x – z 2 y – t 1 0 Û x+z y+t = 0 1 2 x x –z +z 2 y y æ 1 ç 3 -1 Por tanto A = ç– 1 è 3 =1 x = 1/3 =0 y = 1/3 Û –t=0 z = – 1/3 +t=1 t = 2/3 1 3 2 3 ö ÷ ÷ ø

Combinación lineal entre filas y columnas En una matriz A, las filas pueden representarse por F 1, F 2, . . . , Fm y las columnas por C 1, C 2, . . . , Cn. æ a 11 ça ç a 21 A = 31 ç ç. . è am 1 a 12 a 22 a 32. . am 2 a 13. . . a 1 n ö æ F 1 ö çF ÷ a 23. . . a 2 n ÷ 2 ÷ ç ÷ a 33. . . a 3 n = (C 1, C 2, C 3, . . . , Cn) = F 3 ÷ ç ÷. . . ÷ ç. . . ÷ è Fm ø am 3. . . amn ø Se llama combinación lineal de las filas F 1, F 2, F 3. . . , Fm a una expresión de la forma: k 1. F 1 + k 2. F 2 + k 3. F 3 +. . . + km. Fm siendo k 1, k 2, . . . , km números reales. Se llama combinación lineal de las columnas C 1, C 2, C 3. . . , Cn a una expresión de la forma: k 1. C 1 + k 2. C 2 + k 3. C 3 +. . . + kn. Cn siendo k 1, k 2, . . . , kn números reales.

Dependencia lineal entre filas y columnas • Una fila (o columna) de una matriz depende linealmente de otras si es combinación lineal de ellas. • Si entre las filas (o columnas) de una matriz, alguna depende linealmente de otras, se dice que son linealmente dependientes; en caso contrario, son linealmente independientes. æ 2 0 – 1 1 ö Ejemplo: En la matriz A = ç 1 3 1 0 ÷ la tercera fila es combinación lineal de la primera y la è 4 6 1 1ø segunda ya que: F 3 = F 1 + 2 F 2 æ 1 2 4 ö÷ 3 – 1 5 ø las dos filas son linealmente independientes porque ninguna de ellas es igual a una constante por la otra. En cambio: En la matriz B =çè

Método de Gauss-Jordan para el cálculo de la matriz inversa El método de Gauss-Jordan para calcular la matriz inversa de una dada se basa en una triangulación superior y luego otra inferior de la matriz a la cual se le quiere calcular la inversa. Dada una matriz A de orden n, para calcular su inversa hay que transformar la matriz (A I In) mediante transformaciones elementales por filas en la matriz (In I B). La matriz B será la inversa de A. Para aplicar el método se necesita una matriz cuadrada de rango máximo. Sabemos que no siempre una matriz tiene inversa, por lo cual comprobaremos que la matriz tenga rango máximo al aplicar el método de Gauss para realizar la triangulación superior. Si al aplicar el método de Gauss (triangulación inferior) se obtiene una línea de ceros, la matriz no tiene inversa. Las transformaciones elementales son las siguientes: ØPermutar 2 filas ó 2 columnas. ØMultiplicar o dividir una línea por un número no nulo. ØSumar o restar a una línea otra paralela multiplicada por un número no nulo. ØSuprimir las filas o columnas que sean nulas,

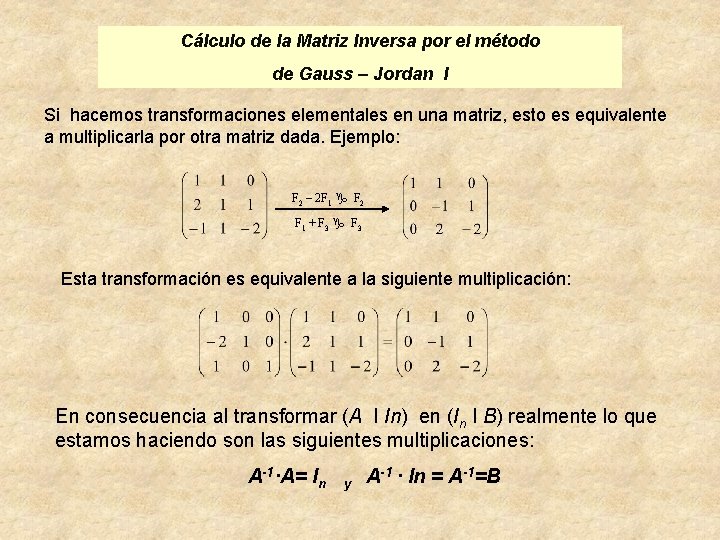
Cálculo de la Matriz Inversa por el método de Gauss – Jordan I Si hacemos transformaciones elementales en una matriz, esto es equivalente a multiplicarla por otra matriz dada. Ejemplo: F 2 – 2 F 1 g F 2 F 1 + F 3 g F 3 Esta transformación es equivalente a la siguiente multiplicación: En consecuencia al transformar (A I In) en (In I B) realmente lo que estamos haciendo son las siguientes multiplicaciones: A-1·A= In y A-1 · In = A-1=B

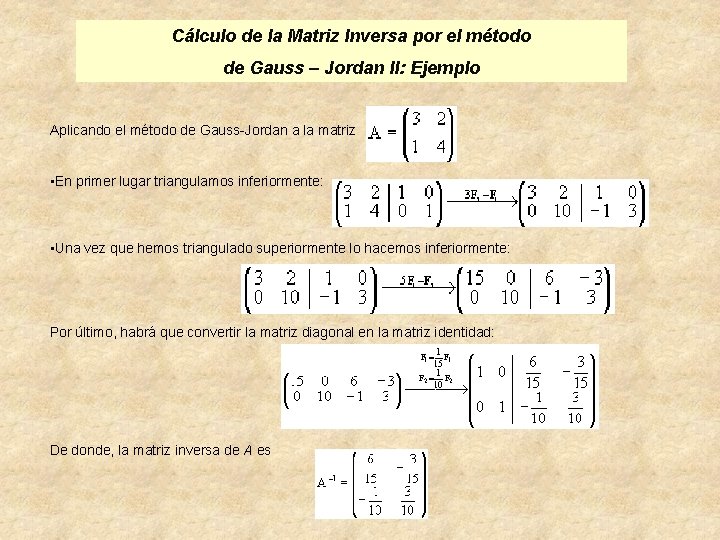
Cálculo de la Matriz Inversa por el método de Gauss – Jordan II: Ejemplo Aplicando el método de Gauss-Jordan a la matriz • En primer lugar triangulamos inferiormente: • Una vez que hemos triangulado superiormente lo hacemos inferiormente: Por último, habrá que convertir la matriz diagonal en la matriz identidad: De donde, la matriz inversa de A es

Cálculo de la Matriz Inversa por el método de Gauss – Jordan III : Ejemplo Aplicando el método de Gauss-Jordan a la matriz se tiene: Como hay una fila completa de ceros, la matriz A no tiene rango máximo, en este caso 2, por tanto no tiene inversa pues es una matriz singular

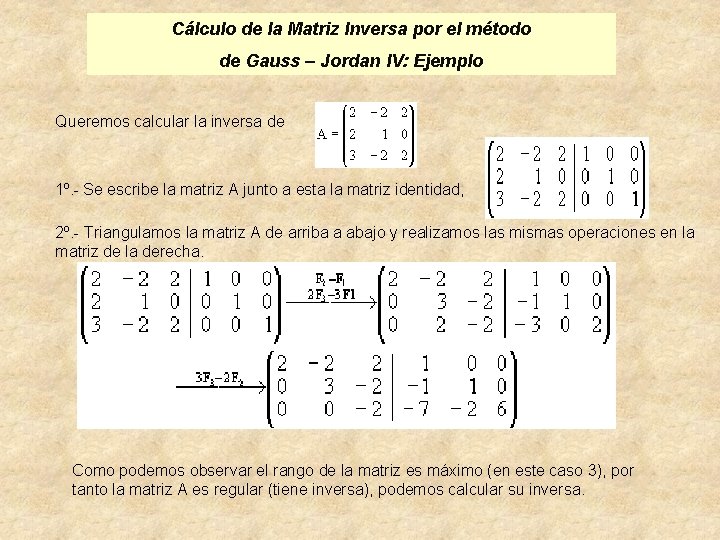
Cálculo de la Matriz Inversa por el método de Gauss – Jordan IV: Ejemplo Queremos calcular la inversa de 1º. - Se escribe la matriz A junto a esta la matriz identidad, 2º. - Triangulamos la matriz A de arriba a abajo y realizamos las mismas operaciones en la matriz de la derecha. Como podemos observar el rango de la matriz es máximo (en este caso 3), por tanto la matriz A es regular (tiene inversa), podemos calcular su inversa.

Cálculo de la Matriz Inversa por el método de Gauss – Jordan V: continuación 3º. - Triangulamos la matriz de abajo a arriba, realizando las mismas operaciones en la matriz de la derecha. 4º. - Por último se divide cada fila por el elemento diagonal correspondiente.

Rango de una matriz • El rango por filas de una matriz es el número de filas linealmente independientes. • El rango por columnas de una matriz es el número de columnas linealmente independientes. • Se puede demostrar que el rango por filas coincide con el rango por columnas en cualquier matriz. A este valor común se le llama rango de la matriz y se representa rg A. Operaciones que no modifican el rango de una matriz • Intercambiar dos filas (o columnas) entre sí. • Multiplicar una fila (o columna) por un número distinto de cero. • Sumar a una fila (o columna) una combinación lineal de otras filas (o columnas).

Dependencia e independencia lineal : filas Vectores fila de una matriz: Las filas de una matriz pueden ser consideradas como vectores. Es posible que sean linealmente Independientes (L. I. ) y es posible que unos dependan linealmente de otros. Por ejemplo: Sus dos filas son linealmente independientes Las dos primeras líneas son L. I. , las otras dos dependen linealmente de las primeras Las dos primeras filas son L. I. la tercera depende linealmente de las dos primeras Se llama rango de una matriz al número de filas Linealmente Independientes

Dependencia e independencia lineal: columnas Vectores columna de una matriz: También las columnas de una matriz pueden ser consideradas como vectores. Podríamos definir rango de la matriz como el número de columnas linealmente independientes, pero aparece la duda de si esa definición puede contradecir en algún caso la anterior. ¿Es posible que en una matriz el número de filas linealmente independientes sea distinto del número de columnas linealmente independiente? . El siguiente teorema nos asegura que no. Teorema En una matriz el número de filas L. I. coincide con el número de columnas L. I. Por esto podemos dar una nueva definición de Rango: Rango de una matriz es el número de filas, o columnas, linealmente independientes.

Ejemplos rango de una matriz escalonada æ 2 0 – 1 1 ö ç ÷ La matriz A = 0 1 1 0 tiene rango 3. ç ÷ è 0 0 1 1ø æ 2 0 - 1 1ö ç ÷ La matriz A = ç 0 1 1 0 ÷ tiene rango 2. ç ÷ è 0 0 ø æ 2 0 - 1 1ö ç ÷ 0 0 1 0 ÷ tiene rango 3. La matriz A = ç ç 0 0 0 1 ÷ è ø æ 0 2 1 1ö ç ÷ La matriz A = ç 0 0 2 0 ÷ tiene rango 2. ç ÷ è 0 0ø æ 0 0 0 1 ö ç ÷ La matriz A = ç 0 0 ÷ tiene rango 1. ç ÷ è 0 0ø

Métodos de cálculo del rango de una matriz El rango de una matriz lo podemos calcular por dos métodos diferentes: v Por el método de Gauss v Usando Determinantes

Cálculo del rango de una matriz por el método de Gauss Transformaciones elementales: Son las transformaciones que podemos realizarle a una matriz sin que su rango varíe. Las transformaciones elementales son las siguientes: ØPermutar 2 filas ó 2 columnas. ØMultiplicar o dividir una línea por un número no nulo. ØSumar o restar a una línea otra paralela multiplicada por un número no nulo. ØSuprimir las filas o columnas que sean nulas, ØSuprimir las filas o columnas que sean proporcionales a otras.

Proceso para el cálculo del rango de una matriz: Método de Gauss æ a 11 ça ç a 21 A= ç 31 ç. . è am 1 a) a 12 a 22 a 32. . am 2 a 13. . . a 1 n ö a 23. . . a 2 n ÷ ÷ a 33. . . a 3 n ÷. . . ÷ am 3. . . amn ø Si es necesario, reordenar filas para que a 11 0 (si esto no fuera posible, aplicar todo el razonamiento a a 12). b) Anular todos los elementos por debajo de a 11: para ello multiplicar la primera fila por –a 21/a 11 y sumar a la segunda, multiplicar la primera fila por –a 31/a 11 y sumar a la tercera, . . multiplicar la primera fila por –am 1/a 11 y sumar a la m-ésima. c) Repetir los pasos anteriores basados en a 22 y, después, en cada aii. d) El proceso termina cuando no quedan más filas o están formadas por ceros.

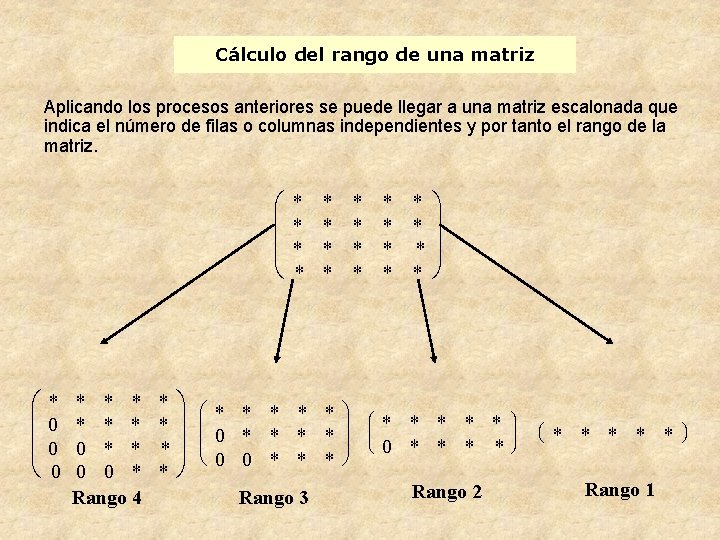
Cálculo del rango de una matriz Aplicando los procesos anteriores se puede llegar a una matriz escalonada que indica el número de filas o columnas independientes y por tanto el rango de la matriz. æ ç ç è * 0 0 0 * * * 0 0 * Rango 4 * ö * ÷ *÷ * ø * * * * æ * * * ö ç ÷ 0 * * ç ÷ è 0 0 * * * ø Rango 3 * * * * æ ç ç è * * ö ÷ ÷ ø * * * ö÷ 0 * * ÷ø Rango 2 æ è * * * Rango 1 ö ø

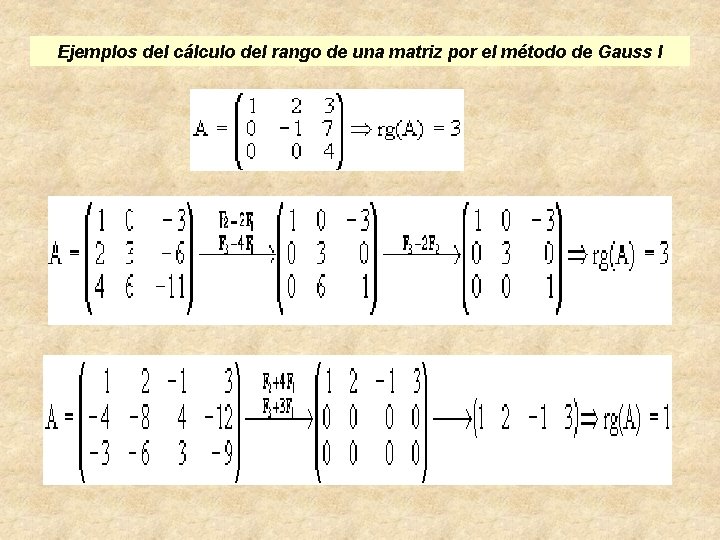
Ejemplos del cálculo del rango de una matriz por el método de Gauss I

Ejemplos del cálculo del rango de una matriz por el método de Gauss II

Condición para que una matriz sea inversible Vamos a estudiar si A = · · · æ ç ç è 2 – 1 ö÷ 4 – 2 ÷ø es inversible: æ ç ç è Ampliamos la matriz A con la matriz identidad: Dividiendo la primera fila por 2: æ ç 1 ç è 4 1 – 2 Restando a la segunda fila la primera por 4: æ ç ç è 2 – 1 1 0 ö÷ ÷ 4 – 2 0 1 ø ö 1 2 0 ÷÷ 0 1 ø ö 1 1 1 – 2 2 0 ÷ ÷ 0 0 – 2 1 ø A no es inversible • Al operar con las filas de A se ha llegado a una matriz de rango distinto a la dimensión de la matriz A. • Por tanto: una matriz cuadrada A de orden n es inversible si y sólo si rg A = n. • De otra forma: A es inversible si y sólo si sus filas (o sus columnas) son linealmente independientes.

Determinantes Definición: Se llama determinante de A al número que se obtiene mediante la suma de los productos de un elemento de cada fila y columna precedidos del signo + o – según la paridad de la permutación que indican sus filas y columnas. Dada una matriz cuadrada se llama determinante de A, y se representa por |A| ó det(A), al número: con (Sn es el grupo de las permutaciones del conjunto {1, 2, . . n }, e i (s) es la signatura de la permutación)

Determinantes de orden 2 y 3 æa a 12 ö 11 ÷ A=ç a a è 21 22 ø Dada una matriz cuadrada de segundo orden: se llama determinante de A al número real: Det( A) = |A| = Ejemplo: a 11 a 12 a 21 a 22 = a 11 · a 22 – a 12 · a 21 3 2 2 1 = 3· 1 - 2· 2 = 3 – 4 = -1 Dada una matriz cuadrada de orden 3 æ a 11 a 12 a 13 ö A = ç a 21 a 22 a 23 ÷ è a 31 a 32 a 33 ø Se llama determinante de A, det (A) o |A|, al número real siguiente: a 11 a 12 a 13 a 21 a 22 a 23 = a 11 a 22 a 33 + a 12 a 23 a 31 + a 13 a 21 a 32 – a 13 a 22 a 31 – a 11 a 23 a 32 – a 12 a 21 a 33. a 31 a 32 a 33

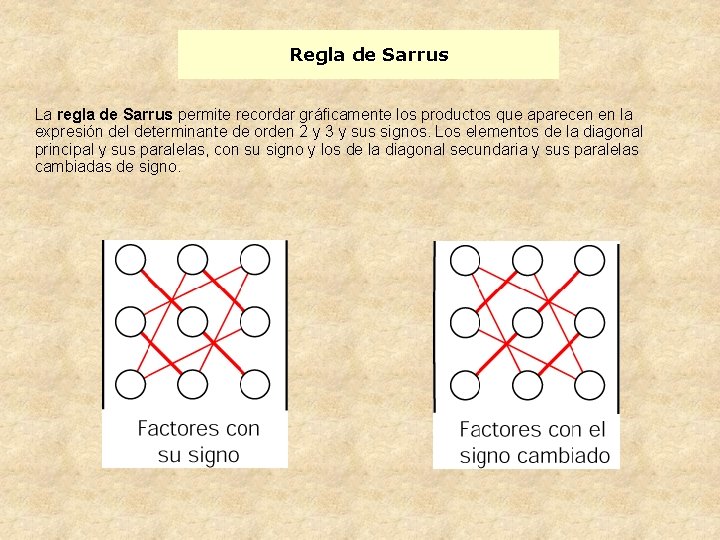
Regla de Sarrus La regla de Sarrus permite recordar gráficamente los productos que aparecen en la expresión del determinante de orden 2 y 3 y sus signos. Los elementos de la diagonal principal y sus paralelas, con su signo y los de la diagonal secundaria y sus paralelas cambiadas de signo.

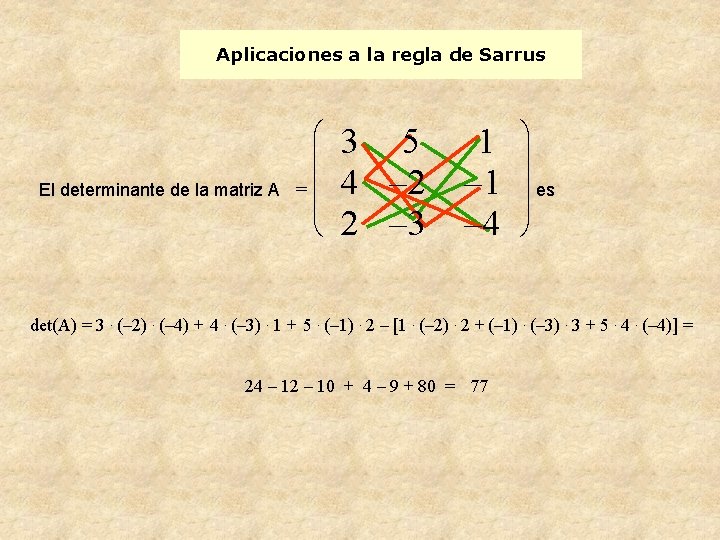
Aplicaciones a la regla de Sarrus El determinante de la matriz A æ ç ç =ç ç è 3 5 4 – 2 2 – 3 1 – 4 ö ÷ ÷ ÷ es ÷ ø det(A) = 3. (– 2). (– 4) + 4. (– 3). 1 + 5. (– 1). 2 – [1. (– 2). 2 + (– 1). (– 3). 3 + 5. 4. (– 4)] = 24 – 12 – 10 + 4 – 9 + 80 = 77

Cálculo de determinantes usando desarrollo por los elementos de una fila o columna • Se llama menor Mij de la matriz A al determinante de la matriz que se obtiene al suprimir en A la fila i-ésima y la columna j-ésima. • Se llama adjunto Aij del elemento aij de la matriz A al número Aij = (– 1)i+j. Mij.

Ejemplos: desarrollos de un determinante de orden 3 Desarrollo por primera columna de un determinante de orden 3 a a 11 a 12 a a 13 a a 22 a 23 21 22 23 = a 11. (-1)1+1 a a 32 33 a a a 31 32 33 +a 21 . (-1)2+1 a a 12 32 a a 13 33 +a 31 . (-1)3+1 a a 12 22 a a Desarrollo por tercera fila de un determinante de orden 3 a 11 a 21 a 31 a 12 a 22 a 32 a 13 a 23 = a 31. (-1)3+1 a 33 a 12 a 22 a 13 a 23 a 11 + a. (-1)3+2 32 a 21 a 13 a 23 a 11 + a. (-1)3+3 33 a 21 a 12 a 22 13 23

Determinante de cualquier orden El determinante de la matriz A de orden n se puede obtener multiplicando los elementos de una fila o columna por sus respectivos adjuntos: det (A) = ai 1. Ai 1 + ai 2 · Ai 2 +. . . + ain. Ain det (A) = a 1 j. A 1 j + a 2 j · A 2 j +. . . + amj. Amj 2 1 Por ejemplo: 3 2 – 1 6 – 1 1 1 – 1 0 sería el desarrollo por la i-ésima fila sería el desarrollo por la j-ésima columna 2 2 1 2 – 1 1 2 2+1 0 3 – 1 3 + 6 · (– 1) – 1 3 1 · (– 1) + = 3 2 0 1 – 1 0 1 1 5 – 3 2 – 1 2 2 – 1 1 2+3 3 – 1 3 + 0 · (– 1)2+4 3 – 1 = + 1 · (– 1) 2 – 1 1 2 – 1 0 – 1 = 1 · 3 + 6 · 5 + 1 · 1 + 0 · (– 1) = 34 – 1

Cálculo inmediato de determinantes (I) I. El determinante de una matriz con dos filas o columnas proporcionales es cero. Ejemplos: æ– 1 4 – 1 ö ç ÷ · El determinante de una matriz A = 3 2 3 ç ÷ es igual a cero porque la tercera y è 2 5 2ø primera columnas son iguales. æ 2 4 – 1 ö ç ÷ · El determinante de una matriz A = 1 – 2 3 ç ÷ es igual a cero porque la tercera fila è 3 – 6 9 ø es igual a la segunda multiplicada por 3. II. El determinante de una matriz con una fila o columnas nulas es cero. Ejemplo: æ– 1 0 – 1 ö ç ÷ El determinante de una matriz A = ç 3 0 3 ÷ es igual a cero porque la segunda columna è 2 0 2ø es nula.

Cálculo inmediato de determinantes (II) III. El determinante de una matriz en que una fila o columna depende linealmente de otras filas o columnas es cero. Ejemplo: æ 2 4 0 ö ç ÷ El determinante de una matriz A = ç 1 3 – 1 ÷ es igual a cero porque la tercera columna es è 3 1 5 ø igual al doble de la primera menos la segunda. IV. El determinante de una matriz triangular es igual al producto de los elementos de su diagonal principal. Ejemplo: El determinante de la matriz æ– 1 0 – 1 ö ç ÷ A = ç 0 2 3 ÷ es igual – 4. è 0 0 2 ø

Cálculo inmediato de determinantes (III) V. El determinante de la matriz unidad es 1 Ejemplos: · æ 1 0 0ö ç ÷ El determinante de la matriz I 3 = ç 0 1 0 ÷ es igual a 1. è 0 0 1ø · æ 1 ç 0 El determinante de la matriz I 5 = ç 0 è 0 0 1 0 0 0 0 0 1 0 0ö 0÷ 0 ÷ es igual a 1. 0÷ 1ø

Propiedades: operaciones con filas y columnas (I) I. Si se multiplican los elementos de una fila o columna de una matriz por un número el determinante de la matriz se multiplica por ese número. Ejemplo: 2 3 2 3 = = 4. . 4 20 1 5 4 1 4 5 II. Si se intercambian entre sí dos filas o dos columnas de una matriz, su determinante cambia de signo. Ejemplo: 1 – 4 1 = – 2 5 5 2

Propiedades: operaciones con filas y columnas (II) III. Al sumar a una fila o columna una combinación lineal de las otras filas o columnas, respectivamente, el valor del determinante no varía. 2 3 – 1 Ejemplo: Si en A = 1 5 2 sumamos a la tercera fila la primera mult iplicada por – 1 más 4 13 4 la segunda multiplicada por – 2, obtenemos: 2 3 1 5 B= 4 + 2 (– 1) + 1(– 2) 13 + 3 (– 1) + 5(– 2) y se cumple que ambos determinantes son iguales: – 1 2 4 + (– 1) + 2(– 2) A=B

Determinantes de operaciones con matrices (I) I. El determinante del producto de dos matrices cuadradas y multiplicables es igual al producto de los determinantes de cada una de ellas. Ejemplo: æ æ 4 1ö 2 0ö ÷ y. B= ç ÷. Se tiene que |A| = – 2 y |B| = 5. è 1 – 1 ø è 3 2ø æ 8 2ö. ÷ y | A. B | = – 10 se observa que | A. B | = |A|. |B| · Como A B = ç è 1 – 1 ø · Sean A = ç II. El producto de los determinantes de dos matrices inversas es 1. Ejemplo: æ æ 1/3 0 ö 3 0ö ÷; entonces A – 1 = ç ÷ è 1 1ø è – 1/3 1 ø – 1 · Como | A | = 3 y | A | = 1/3, se observa que | A | · Sea A = ç . |A – 1 |=1

Operaciones con matrices (II) III. Al trasponer una matriz su determinante no varía. Ejemplo: · æ 2 0 – 2 ö æ 2 1 3ö t Sea A = ç 1 1 3 ÷. Entonces A = ç 0 1 0 ÷ è 3 0 2 ø è– 2 3 2 ø · Se cumple que | A | = | At | VI. Si se multiplica una matriz cuadrada de orden n por un número, el nuevo determinante es igual al anterior multiplicado por la potencia n-ésima del número. Ejemplo: æ 2 0 – 2ö æ 4 0 – 4ö ç ÷ 3 Se cumple que: 2 ç 1 1 3 ÷ = ç 2 2 6 ÷ = 2 è 3 0 2ø è 6 0 4ø æ 2 0 – 2ö ç ÷ 1 1 3 ç ÷ è 3 0 2ø

Operaciones con matrices (III) V. - Si una fila o columna es suma de varios sumandos, se descompone en tantos determinantes como sumandos haya æ a 11 a 12 + b 12 a 13 ö Si A = ç a 21 a 22 + b 22 a 23 ÷ è a 31 a 32 + b 32 a 33 ø se cumple que: a 11 a 12 + b 12 a 13 a 11 a 12 a 13 a 11 b 12 a 13 a 21 a 22 + b 22 a 23 = a 21 a 22 a 23 + a 21 b 22 a 23 a 31 a 32 + b 32 a 33 a 31 a 32 a 33 a 31 b 32 a 33 Ejemplo: æ 2 3 ç · Sea A = 1 5 ç è 4 13 · Y se tiene que: 3 – 1 ö æ 2 ç ÷ 1 5 2 ç ÷ = è 4 13 4 ø – 1 ö ÷ 2 ÷. Entonces se cumple que | A | = 7 4ø 3 – 1 ö æ 1+1 æ 1 3 – 1 ö æ 1 ç ÷ ç 3 – 2 5 2 3 5 2 = + ç ÷ ç– 2 è 1 + 3 13 4 ø è 1 13 4 ø è 3 3 – 1 ö ÷ 5 2 ÷ = (-70) + 77 13 4 ø

Obtención de la matiz inversa mediante determinantes (I) • La matriz cuadrada A tiene inversa si y sólo si | A | ≠ 0. • Se llama “Adjunto Ai, j” del elemento “ai, j” al determinante del menor Mi, j multiplicado por (-1)i+j • Dada la matriz cuadrada A, se llama “matriz adjunta” de A y se representa la matriz que se obtiene al sustituir cada elemento aij por su adjunto Aij. æ 2 -2 2 ö ç ÷ Ejemplo: Dada la matriz (A) = ç 2 1 0 ÷ , su adjunta sería: è 3 -2 2 ø æ 1 ç – 2 adj (A)= ç – – 2 ç ç – 2 è 1 0 2 2 0 – 3 2 2 1 3 – 2 2 2 3 2 2 – 3 – 2 2 0 2 2 – 2 0 2 – 2 2 1 ö ÷ ÷ ÷ ø = æ 2 – 4 – 7 ö ç ÷ 0 – 2 ç ÷ è – 2 4 6 ø adj (A), a

Obtención de la matiz inversa mediante determinantes (II) Esto es fácil probarlo puesto que sabemos que la suma de los productos de los elementos de una fila por sus adjuntos es el valor del determinante, y que la suma de los productos de los elementos de una fila por los adjuntos de otra fila diferente es 0 æ 2 – 2 2 ö ç ÷ Ejemplo: Dada la matriz A = ç 2 1 0 ÷ , pretendemos encontrar su inversa: è 3 – 2 2 ø La matriz A tiene inversa ya que: det(A) = – 2 0 æ 2 – 4 – 7 ö Ya hemos visto que: adj (A) = ç 0 – 2 ÷ è – 2 4 6 ø æ 2 0 – 2 ö ç ÷ Entonces: [adj (A)] = ç – 4 – 2 4 ÷ è – 7 – 2 6 ø t æ 2 0 – 2 ö æ – 1 0 1 ö 1 1 ç ÷ t Por lo tanto: A = | A | [adj (A)] = – 2 ç – 4 – 2 4 ÷ = ç 2 1 – 2 ÷ è – 7 – 2 6 ø è 7/2 1 – 3 ø – 1

Calculo de la matriz inversa por el método de los adjuntos I

Calculo de la matriz inversa por el método de los adjuntos II

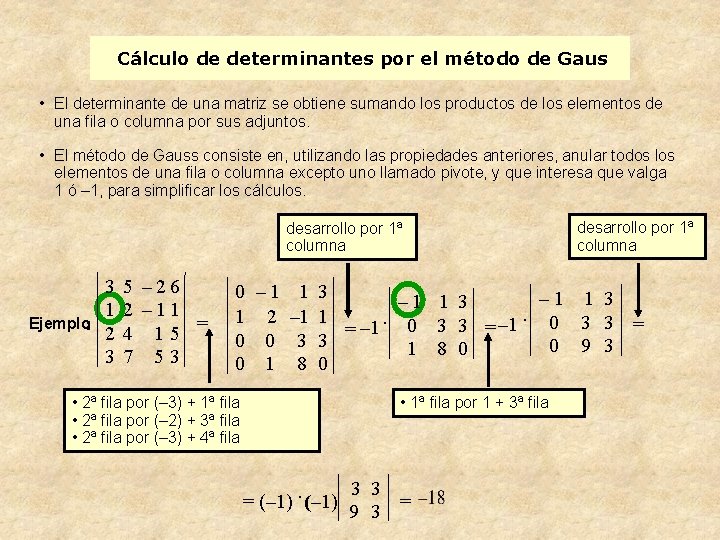
Cálculo de determinantes por el método de Gaus • El determinante de una matriz se obtiene sumando los productos de los elementos de una fila o columna por sus adjuntos. • El método de Gauss consiste en, utilizando las propiedades anteriores, anular todos los elementos de una fila o columna excepto uno llamado pivote, y que interesa que valga 1 ó – 1, para simplificar los cálculos. desarrollo por 1ª columna 3 1 Ejemplo: 2 3 5 – 26 2 – 11 4 15 = 7 53 desarrollo por 1ª columna 0 – 1 1 3. 1 2 – 1 1. 0 3 3 = = – 1 0 3 3 = – 1 0 0 3 3 0 9 3 1 8 0 0 1 8 0 • 2ª fila por (– 3) + 1ª fila • 2ª fila por (– 2) + 3ª fila • 2ª fila por (– 3) + 4ª fila • 1ª fila por 1 + 3ª fila 3 3 (– 1) = (– 1) 9 3 =.