UNIDAD IV DETERMINANTES DE UNA MATRIZ Determinantes Definicin

UNIDAD IV DETERMINANTES DE UNA MATRIZ

Determinantes Definición: Se llama determinante de A al número que se obtiene mediante la suma de los productos de un elemento de cada fila y columna precedidos del signo + o – según la paridad de la permutación que indican sus filas y columnas. Dada una matriz cuadrada se llama determinante de A, y se representa por |A| ó det(A), al número: con (Sn es el grupo de las permutaciones del conjunto {1, 2, . . n }, e i (s) es la signatura de la permutación)

Determinantes de orden 2 y 3 æa a 12 ö 11 ÷ A=ç a a è 21 22 ø Dada una matriz cuadrada de segundo orden: se llama determinante de A al número real: Det( A) = |A| = Ejemplo: a 11 a 12 a 21 a 22 = a 11 · a 22 – a 12 · a 21 3 2 2 1 = 3· 1 - 2· 2 = 3 – 4 = -1 Dada una matriz cuadrada de orden 3 æ a 11 a 12 a 13 ö A = ç a 21 a 22 a 23 ÷ è a 31 a 32 a 33 ø Se llama determinante de A, det (A) o |A|, al número real siguiente: a 11 a 12 a 13 a 21 a 22 a 23 = a 11 a 22 a 33 + a 12 a 23 a 31 + a 13 a 21 a 32 – a 13 a 22 a 31 – a 11 a 23 a 32 – a 12 a 21 a 33. a 31 a 32 a 33

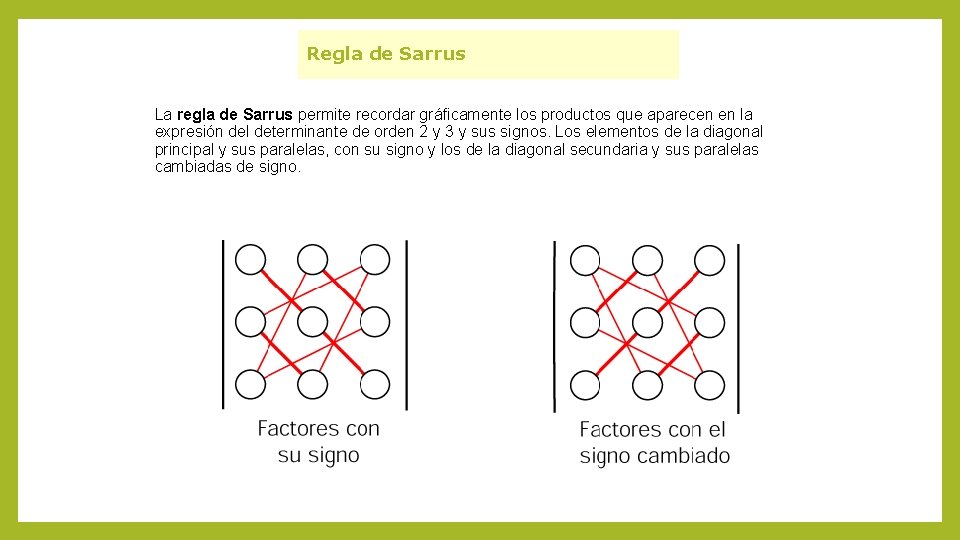
Regla de Sarrus La regla de Sarrus permite recordar gráficamente los productos que aparecen en la expresión del determinante de orden 2 y 3 y sus signos. Los elementos de la diagonal principal y sus paralelas, con su signo y los de la diagonal secundaria y sus paralelas cambiadas de signo.

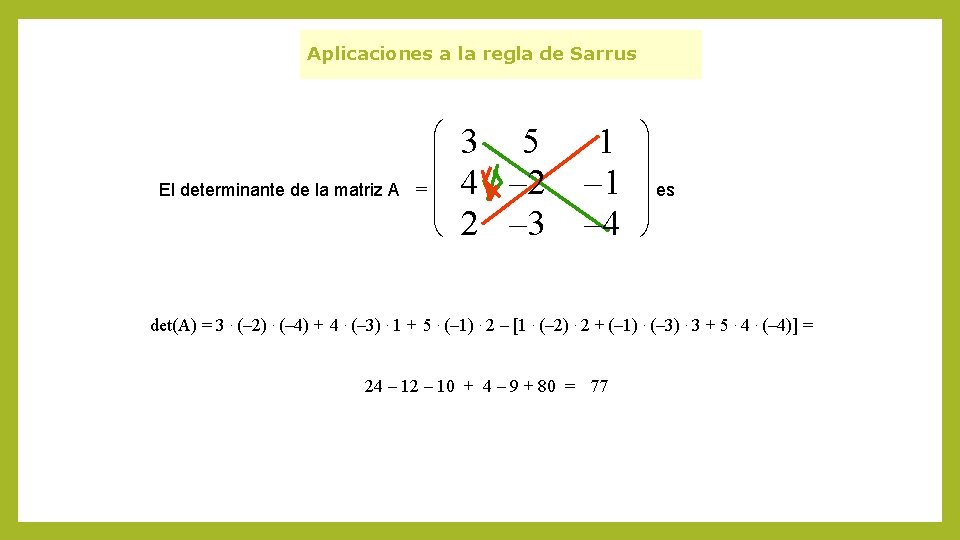
Aplicaciones a la regla de Sarrus El determinante de la matriz A æ ç ç =ç ç è 3 5 4 – 2 2 – 3 1 – 4 ö ÷ ÷ ÷ es ÷ ø det(A) = 3. (– 2). (– 4) + 4. (– 3). 1 + 5. (– 1). 2 – [1. (– 2). 2 + (– 1). (– 3). 3 + 5. 4. (– 4)] = 24 – 12 – 10 + 4 – 9 + 80 = 77

Cálculo de determinantes usando desarrollo por los elementos de una fila o columna • Se llama menor Mij de la matriz A al determinante de la matriz que se obtiene al suprimir en A la fila i-ésima y la columna j-ésima. • Se llama adjunto Aij del elemento aij de la matriz A al número Aij = (– 1)i+j. Mij.

Ejemplos: desarrollos de un determinante de orden 3 Desarrollo por primera columna de un determinante de orden 3 a a 11 a 12 a a 13 a a 22 a 23 21 22 23 = a 11. (-1)1+1 a a 32 33 a a a 31 32 33 +a 21 . (-1)2+1 a a 12 32 a a 13 33 +a 31 . (-1)3+1 a a 12 22 a a Desarrollo por tercera fila de un determinante de orden 3 a 11 a 21 a 31 a 12 a 22 a 32 a 13 a 23 = a 31. (-1)3+1 a 33 a 12 a 22 a 13 a 23 a 11 + a. (-1)3+2 32 a 21 a 13 a 23 a 11 + a. (-1)3+3 33 a 21 a 12 a 22 13 23

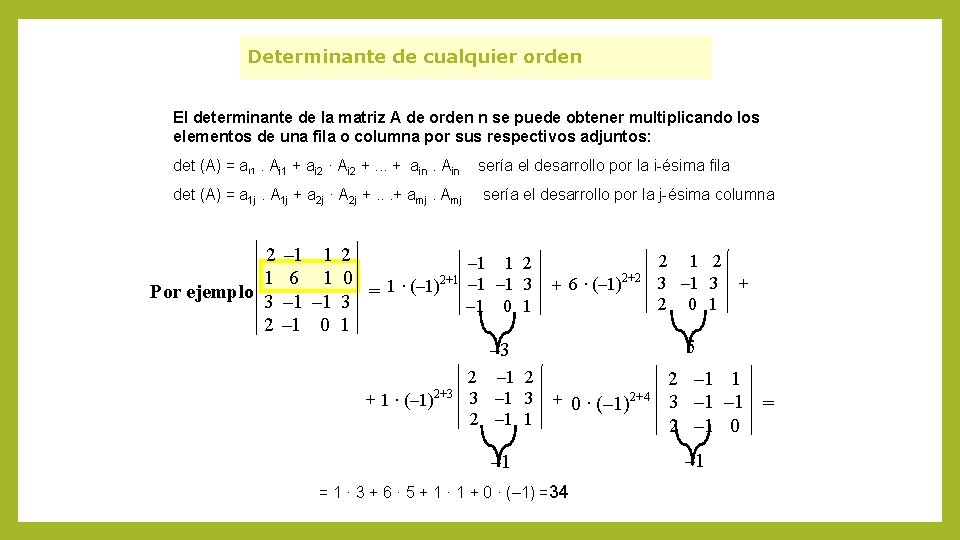
Determinante de cualquier orden El determinante de la matriz A de orden n se puede obtener multiplicando los elementos de una fila o columna por sus respectivos adjuntos: det (A) = ai 1. Ai 1 + ai 2 · Ai 2 +. . . + ain. Ain det (A) = a 1 j. A 1 j + a 2 j · A 2 j +. . . + amj. Amj 2 1 Por ejemplo: 3 2 sería el desarrollo por la i-ésima fila sería el desarrollo por la j-ésima columna – 1 1 2 2 1 2 – 1 1 2 2+1 6 1 0 3 – 1 3 + 6 · (– 1) – 1 3 1 · (– 1) + = – 1 3 2 0 1 – 1 0 1 5 – 3 2 – 1 2 2 – 1 1 2+3 3 – 1 3 + 0 · (– 1)2+4 3 – 1 = + 1 · (– 1) 2 – 1 1 2 – 1 0 – 1 = 1 · 3 + 6 · 5 + 1 · 1 + 0 · (– 1) = 34 – 1

Cálculo inmediato de determinantes (I) I. El determinante de una matriz con dos filas o columnas proporcionales es cero. Ejemplos: æ– 1 4 – 1 ö ç ÷ · El determinante de una matriz A = 3 2 3 ç ÷ es igual a cero porque la tercera y è 2 5 2ø primera columnas son iguales. æ 2 4 – 1 ö ç ÷ · El determinante de una matriz A = 1 – 2 3 ç ÷ es igual a cero porque la tercera fila è 3 – 6 9 ø es igual a la segunda multiplicada por 3. II. El determinante de una matriz con una fila o columnas nulas es cero. Ejemplo: æ– 1 0 – 1 ö ç ÷ El determinante de una matriz A = ç 3 0 3 ÷ es igual a cero porque la segunda columna è 2 0 2ø es nula.

Cálculo inmediato de determinantes (II) III. El determinante de una matriz en que una fila o columna depende linealmente de otras filas o columnas es cero. Ejemplo: æ 2 4 0 ö ç ÷ El determinante de una matriz A = ç 1 3 – 1 ÷ es igual a cero porque la tercera columna es è 3 1 5 ø igual al doble de la primera menos la segunda. IV. El determinante de una matriz triangular es igual al producto de los elementos de su diagonal principal. Ejemplo: El determinante de la matriz æ– 1 0 – 1 ö ç ÷ A = ç 0 2 3 ÷ es igual – 4. è 0 0 2 ø

Cálculo inmediato de determinantes (III) V. El determinante de la matriz unidad es 1 Ejemplos: · æ 1 0 0ö ç ÷ El determinante de la matriz I 3 = ç 0 1 0 ÷ es igual a 1. è 0 0 1ø · æ 1 ç 0 El determinante de la matriz I 5 = ç 0 è 0 0 1 0 0 0 0 0 1 0 0ö 0÷ 0 ÷ es igual a 1. 0÷ 1ø

Propiedades: operaciones con filas y columnas (I) I. Si se multiplican los elementos de una fila o columna de una matriz por un número el determinante de la matriz se multiplica por ese número. Ejemplo: 2 3 2 3 = = 4. . 4 20 1 5 4 1 4 5 II. Si se intercambian entre sí dos filas o dos columnas de una matriz, su determinante cambia de signo. Ejemplo: 1 – 4 1 = – 2 5 5 2

Propiedades: operaciones con filas y columnas (II) III. Al sumar a una fila o columna una combinación lineal de las otras filas o columnas, respectivamente, el valor del determinante no varía. 2 3 – 1 Ejemplo: Si en A = 1 5 2 sumamos a la tercera fila la primera mult iplicada por – 1 más 4 13 4 la segunda multiplicada por – 2, obtenemos: 2 3 1 5 B= 4 + 2 (– 1) + 1(– 2) 13 + 3 (– 1) + 5(– 2) y se cumple que ambos determinantes son iguales: – 1 2 4 + (– 1) + 2(– 2) A=B

Determinantes de operaciones con matrices (I) I. El determinante del producto de dos matrices cuadradas y multiplicables es igual al producto de los determinantes de cada una de ellas. Ejemplo: æ æ 4 1ö 2 0ö ÷ y. B= ç ÷. Se tiene que |A| = – 2 y |B| = 5. è 1 – 1 ø è 3 2ø æ 8 2ö. ÷ y | A. B | = – 10 se observa que | A. B | = |A|. |B| · Como A B = ç è 1 – 1 ø · Sean A = ç II. El producto de los determinantes de dos matrices inversas es 1. Ejemplo: æ æ 1/3 0 ö 3 0ö ÷; entonces A – 1 = ç ÷ è 1 1ø è – 1/3 1 ø – 1 · Como | A | = 3 y | A | = 1/3, se observa que | A | · Sea A = ç . |A – 1 |=1

Operaciones con matrices (II) III. Al trasponer una matriz su determinante no varía. Ejemplo: · æ 2 0 – 2 ö æ 2 1 3ö t Sea A = ç 1 1 3 ÷. Entonces A = ç 0 1 0 ÷ è 3 0 2 ø è– 2 3 2 ø · Se cumple que | A | = | At | VI. Si se multiplica una matriz cuadrada de orden n por un número, el nuevo determinante es igual al anterior multiplicado por la potencia n-ésima del número. Ejemplo: æ 2 0 – 2ö æ 4 0 – 4ö ç ÷ 3 Se cumple que: 2 ç 1 1 3 ÷ = ç 2 2 6 ÷ = 2 è 3 0 2ø è 6 0 4ø æ 2 0 – 2ö ç ÷ 1 1 3 ç ÷ è 3 0 2ø

Operaciones con matrices (III) V. - Si una fila o columna es suma de varios sumandos, se descompone en tantos determinantes como sumandos haya æ a 11 a 12 + b 12 a 13 ö Si A = ç a 21 a 22 + b 22 a 23 ÷ è a 31 a 32 + b 32 a 33 ø se cumple que: a 11 a 12 + b 12 a 13 a 11 a 12 a 13 a 11 b 12 a 13 a 21 a 22 + b 22 a 23 = a 21 a 22 a 23 + a 21 b 22 a 23 a 31 a 32 + b 32 a 33 a 31 a 32 a 33 a 31 b 32 a 33 Ejemplo: æ 2 3 ç · Sea A = 1 5 ç è 4 13 · Y se tiene que: 3 – 1 ö æ 2 ç ÷ 1 5 2 ç ÷ = è 4 13 4 ø – 1 ö ÷ 2 ÷. Entonces se cumple que | A | = 7 4ø 3 – 1 ö æ 1+1 æ 1 3 – 1 ö æ 1 ç ÷ ç 3 – 2 5 2 3 5 2 = + ç ÷ ç– 2 è 1 + 3 13 4 ø è 1 13 4 ø è 3 3 – 1 ö ÷ 5 2 ÷ = (-70) + 77 13 4 ø

Rango de una matriz por determinantes I Se llama “menor” de orden p de una matriz al determinante que resulta de eliminar ciertas filas y columnas hasta quedar una matriz cuadrada de orden p. Es decir, al determinante de cualquier submatriz cuadrada de A (submatriz obtenida suprimiendo alguna fila o columna de la matriz A). En una matriz cualquiera A m×n puede haber varios menores de un cierto orden p dado. Definición: El RANGO (o característica) de una matriz es el orden del mayor de los menores distintos de cero. El rango o característica de una matriz A se representa por rg(A). Consecuencias El rango no puede ser mayor al número de filas o de columnas. Las filas o columnas de una matriz cuadrada son linealmente dependientes si y sólo si su determinante es cero.

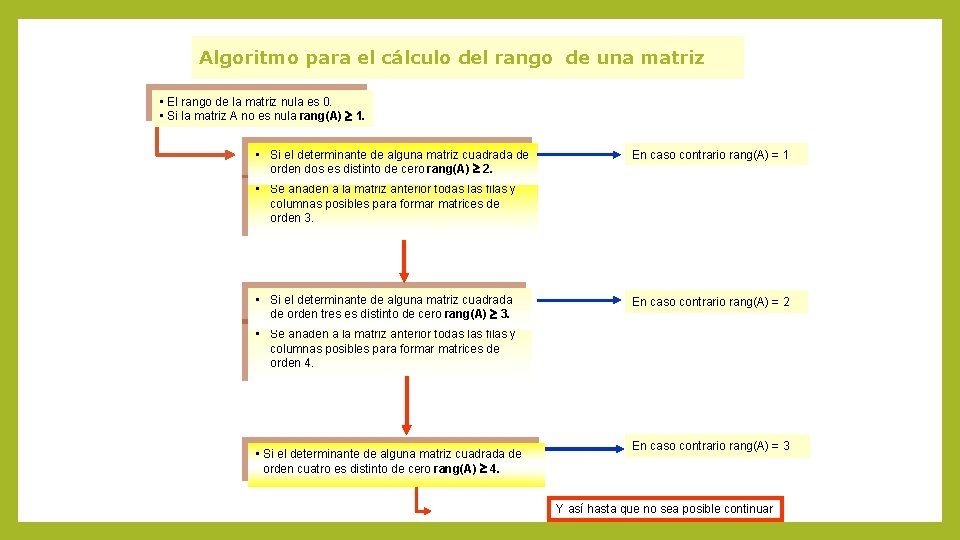
Algoritmo para el cálculo del rango de una matriz • El rango de la matriz nula es 0. • Si la matriz A no es nula rang(A) 1. • Si el determinante de alguna matriz cuadrada de orden dos es distinto de cero rang(A) 2. En caso contrario rang(A) = 1 • Se añaden a la matriz anterior todas las filas y columnas posibles para formar matrices de orden 3. • Si el determinante de alguna matriz cuadrada de orden tres es distinto de cero rang(A) 3. En caso contrario rang(A) = 2 • Se añaden a la matriz anterior todas las filas y columnas posibles para formar matrices de orden 4. • Si el determinante de alguna matriz cuadrada de orden cuatro es distinto de cero rang(A) 4. En caso contrario rang(A) = 3 Y así hasta que no sea posible continuar

Obtención de la matiz inversa mediante determinantes (I) • La matriz cuadrada A tiene inversa si y sólo si | A | ≠ 0. • Se llama “Adjunto Ai, j” del elemento “ai, j” al determinante del menor Mi, j multiplicado por (-1)i+j • Dada la matriz cuadrada A, se llama “matriz adjunta” de A y se representa la matriz que se obtiene al sustituir cada elemento aij por su adjunto Aij. æ 2 -2 2 ö ç ÷ Ejemplo: Dada la matriz (A) = ç 2 1 0 ÷ , su adjunta sería: è 3 -2 2 ø æ 1 ç – 2 adj (A)= ç – – 2 ç ç – 2 è 1 0 2 2 0 – 3 2 2 1 3 – 2 2 2 3 2 2 – 3 – 2 2 0 2 2 – 2 0 2 – 2 2 1 ö ÷ ÷ ÷ ø = æ 2 – 4 – 7 ö ç ÷ 0 – 2 ç ÷ è – 2 4 6 ø adj (A), a

Obtención de la matiz inversa mediante determinantes (II) Si se cumple que | A | ≠ 0 entonces la matriz inversa A-1 es igual a: – 1 t t 1 1 A = | A | adj(A ) = | A | [adj(A)] Esto es fácil probarlo puesto que sabemos que la suma de los productos de los elementos de una fila por sus adjuntos es el valor del determinante, y que la suma de los productos de los elementos de una fila por los adjuntos de otra fila diferente es 0 æ 2 – 2 2 ö ç ÷ Ejemplo: Dada la matriz A = ç 2 1 0 ÷ , pretendemos encontrar su inversa: è 3 – 2 2 ø La matriz A tiene inversa ya que: det(A) = – 2 0 æ 2 – 4 – 7 ö Ya hemos visto que: adj (A) = ç 0 – 2 ÷ è – 2 4 6 ø æ 2 0 – 2 ö ç ÷ Entonces: [adj (A)] = ç – 4 – 2 4 ÷ è – 7 – 2 6 ø t æ 2 0 – 2 ö æ – 1 0 1 ö 1 1 ç ÷ t Por lo tanto: A = | A | [adj (A)] = – 2 ç – 4 – 2 4 ÷ = ç 2 1 – 2 ÷ è – 7 – 2 6 ø è 7/2 1 – 3 ø – 1

Calculo de la matriz inversa por el método de los adjuntos I

Calculo de la matriz inversa por el método de los adjuntos II

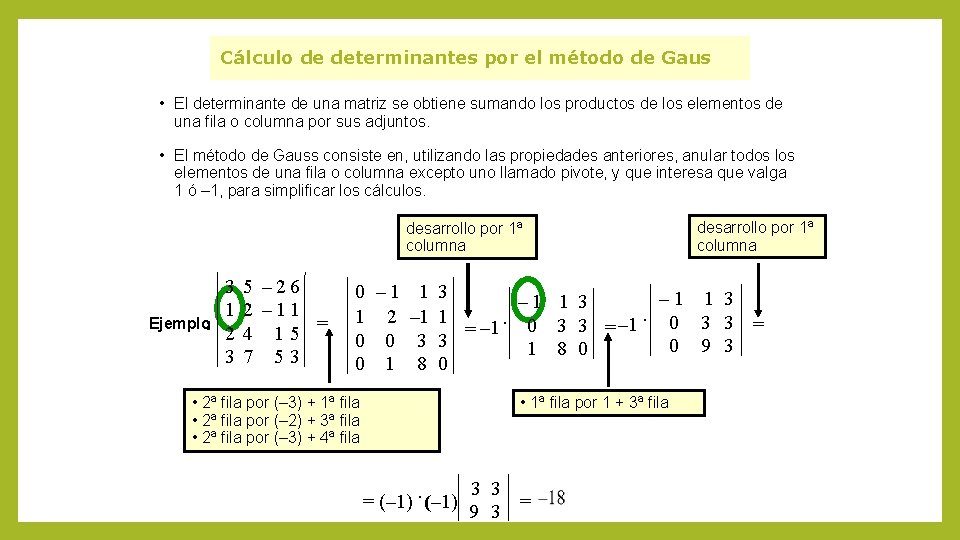
Cálculo de determinantes por el método de Gaus • El determinante de una matriz se obtiene sumando los productos de los elementos de una fila o columna por sus adjuntos. • El método de Gauss consiste en, utilizando las propiedades anteriores, anular todos los elementos de una fila o columna excepto uno llamado pivote, y que interesa que valga 1 ó – 1, para simplificar los cálculos. desarrollo por 1ª columna 3 1 Ejemplo: 2 3 5 – 26 2 – 11 4 15 = 7 53 desarrollo por 1ª columna 0 – 1 1 3. 1 2 – 1 1. 0 3 3 = = – 1 0 3 3 = – 1 0 0 3 3 0 9 3 1 8 0 0 1 8 0 • 2ª fila por (– 3) + 1ª fila • 2ª fila por (– 2) + 3ª fila • 2ª fila por (– 3) + 4ª fila • 1ª fila por 1 + 3ª fila 3 3 (– 1) = (– 1) 9 3 =.