Mathematics Statistics Topic 7 Estimation Topic Goals After

Mathematics & Statistics Topic 7 Estimation

Topic Goals After completing this topic, you should be able to: § Distinguish between a point estimate and a confidence interval estimate § Construct and interpret a confidence interval estimate for a single population mean using both the Z and t distributions § Form and interpret a confidence interval estimate for a single population proportion § Form and interpret a confidence interval estimate for a single population variance

Estimation § § § Last week we looked at the distribution of sample statistics. . . given the value of a population parameter. In real-life situations we don’t know the true value of the population parameter. . . so the question is: Can we say something about the value of the population parameter. . . given an observed value of a sample statistic?

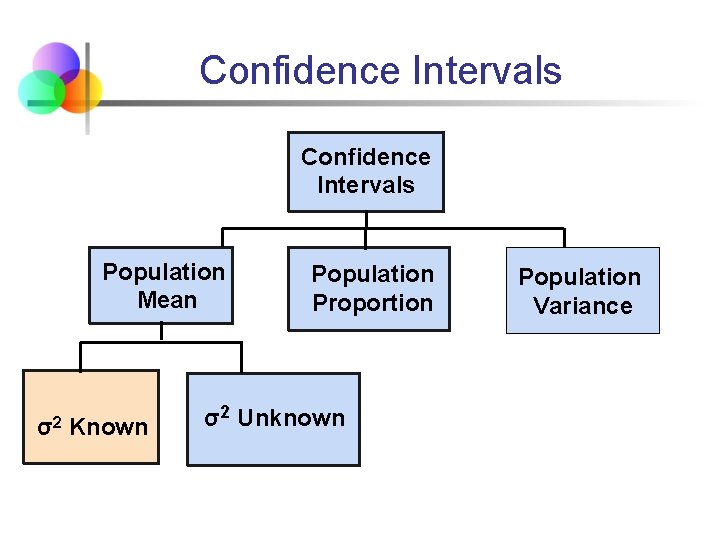
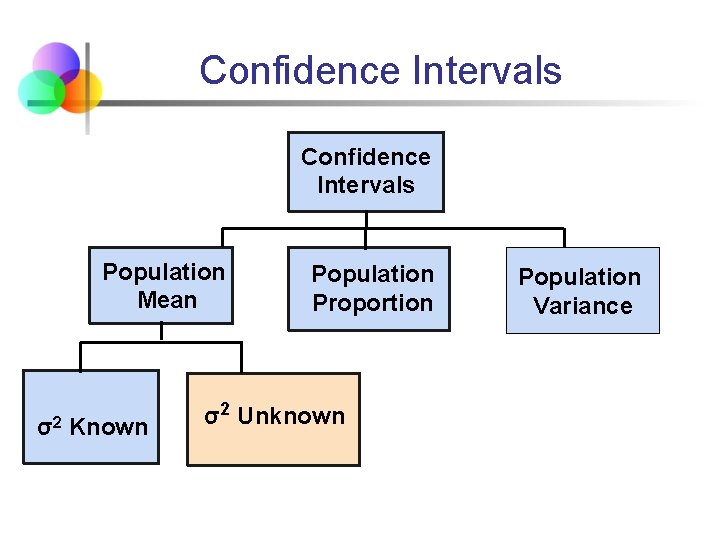
Confidence Intervals Content of this topic § Confidence Intervals for the Population Mean, μ § § when Population Variance σ2 is Known (Section 8. 2) when Population Variance σ2 is Unknown (Section 8. 3) Confidence Intervals for the Population Proportion, p (large samples) (Section 8. 4) Confidence Intervals for the Population Variance, σ2 (Section 9. 4)

Definitions § An estimator of a population parameter is § § § a random variable that depends on sample information. . . whose value provides an approximation to this unknown parameter A specific value of that random variable is called an estimate

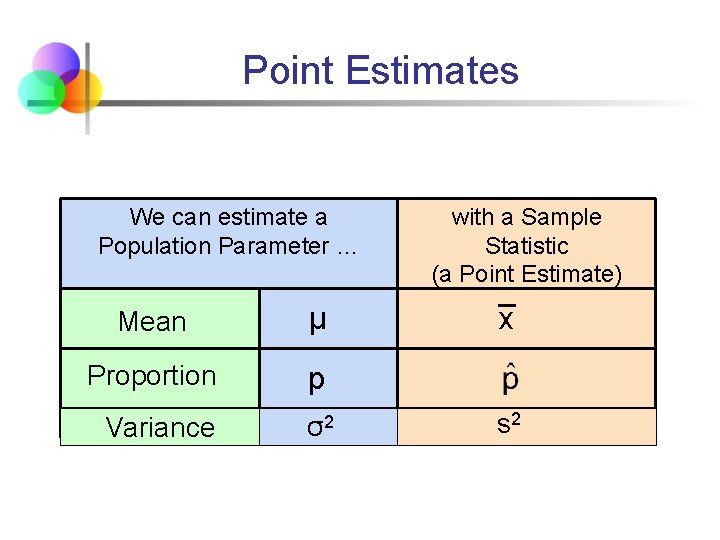
Point Estimates We can estimate a Population Parameter … Mean μ Proportion p Variance σ2 with a Sample Statistic (a Point Estimate) x s 2

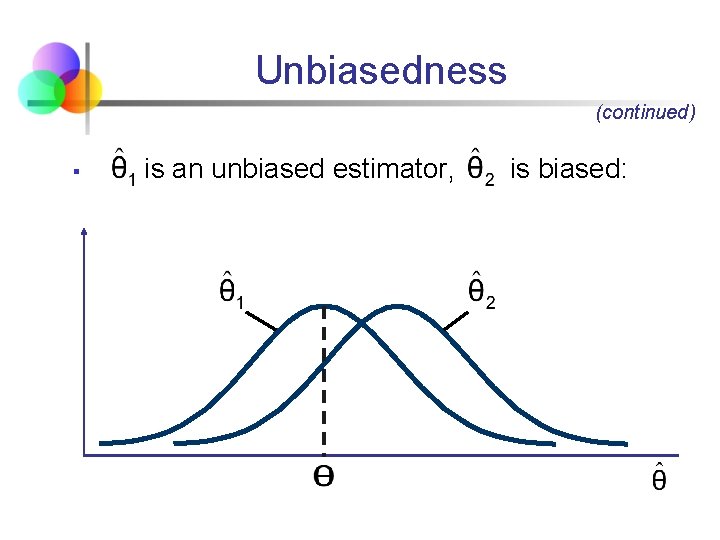
Unbiasedness § § A point estimator is said to be an unbiased estimator of the parameter if the expected value, or mean, of the sampling distribution of is , Examples: § The sample mean is an unbiased estimator of μ 2 § The sample variance is an unbiased estimator of σ § The sample proportion is an unbiased estimator of p

Unbiasedness (continued) § is an unbiased estimator, is biased:

Most Efficient Estimator § § § Suppose there are several unbiased estimators of The most efficient estimator or the minimum variance unbiased estimator of is the unbiased estimator with the smallest variance Let and be two unbiased estimators of , based on the same number of sample observations. Then, § § is said to be more efficient than The relative efficiency of of their variances: if with respect to is the ratio

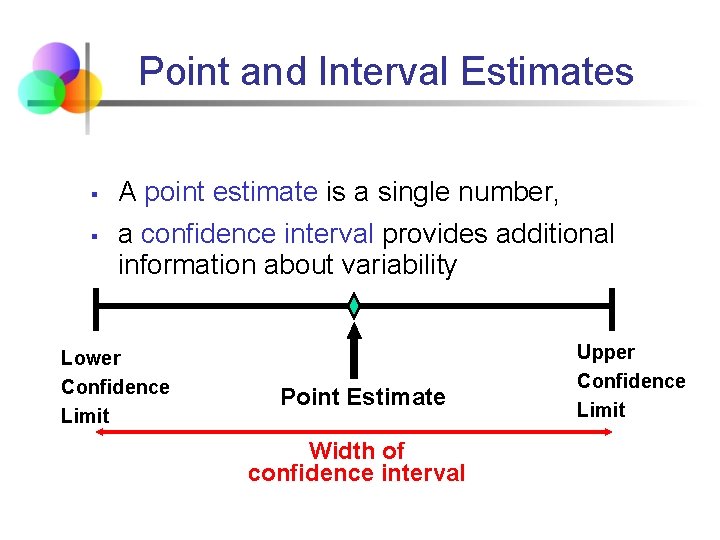
Point and Interval Estimates § § A point estimate is a single number, a confidence interval provides additional information about variability Lower Confidence Limit Point Estimate Width of confidence interval Upper Confidence Limit

Confidence Intervals § § § How much uncertainty is associated with a point estimate of a population parameter? An interval estimate provides more information about a population characteristic than does a point estimate Such interval estimates are called confidence intervals

Confidence Interval Estimate § An interval gives a range of values: § § Takes into consideration variation in sample statistics from sample to sample Based on observation from 1 sample Gives information about closeness to unknown population parameters Stated in terms of level of confidence § Can never be 100% confident

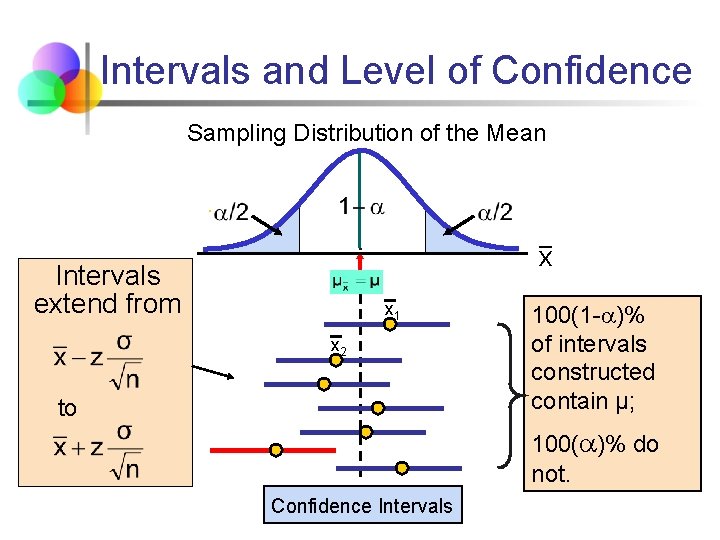
Confidence Interval and Confidence Level § § If P(a < < b) = 1 - then the interval from a to b is called a 100(1 - )% confidence interval of . The quantity (1 - ) is called the confidence level of the interval ( between 0 and 1) § § In repeated samples of the population, the true value of the parameter would be contained in 100(1 - )% of intervals calculated this way. The confidence interval calculated in this manner is written as a < < b with 100(1 - )% confidence

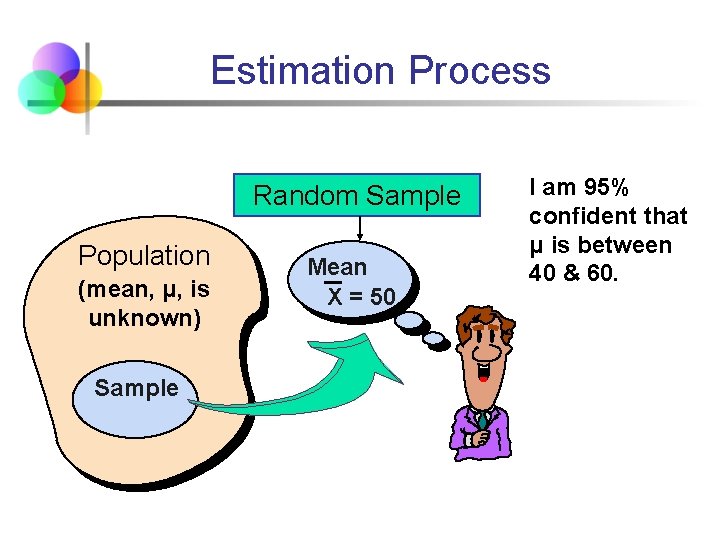
Estimation Process Random Sample Population (mean, μ, is unknown) Sample Mean X = 50 I am 95% confident that μ is between 40 & 60.

Confidence Level, (1 - ) (continued) § § § Suppose confidence level = 95% Also written (1 - ) = 0. 95 A relative frequency interpretation: § § From repeated samples, 95% of all the confidence intervals that can be constructed will contain the unknown true parameter A specific interval either will contain or will not contain the true parameter § § The procedure used leads to a correct interval in 95% of the time. . . but this does not guarantee anything about a particular sample.

General Formula § The general formula for all confidence intervals is: Point Estimate (Reliability Factor)(Standard deviation) § The value of the reliability factor depends on the desired level of confidence

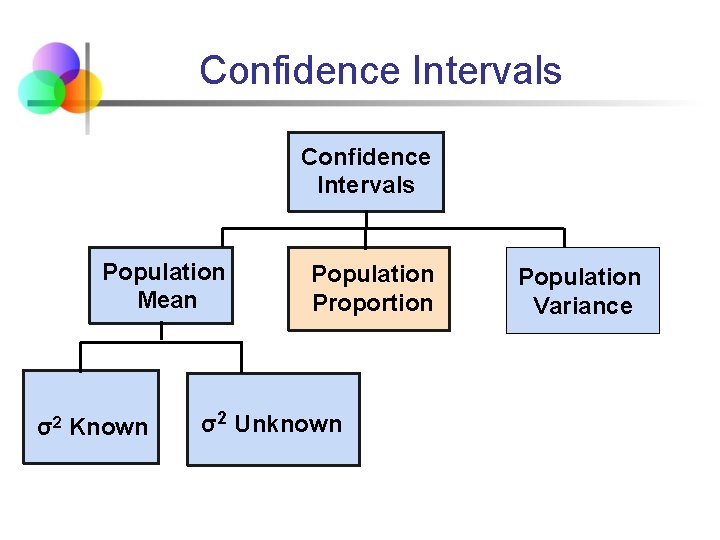
Confidence Intervals Population Mean σ2 Known Population Proportion σ2 Unknown Population Variance

Confidence Interval for μ (σ2 Known) § Assumptions § § Population variance σ2 is known Population is normally distributed. . . . or large sample so that CLT can be used. Confidence interval estimate: (where z /2 is the normal distribution value for a probability of /2 in each tail)

Example § § A sample of 11 circuits from a large normal population has a mean resistance of 2. 20 ohms. We know from past testing that the population standard deviation is 0. 35 ohms. Determine a 95% confidence interval for the true mean resistance of the population.

Example (continued) § § A sample of 11 circuits from a large normal population has a mean resistance of 2. 20 ohms. We know from past testing that the population standard deviation is. 35 ohms. Solution:

Interpretation § § We are 95% confident that the true mean resistance is between 1. 9932 and 2. 4068 ohms Although the true mean may or may not be in this interval, 95% of intervals formed in this manner will contain the true mean

Margin of Error § § § The confidence interval, Can also be written as where ME is called the margin of error The interval width, w, is equal to twice the margin of error

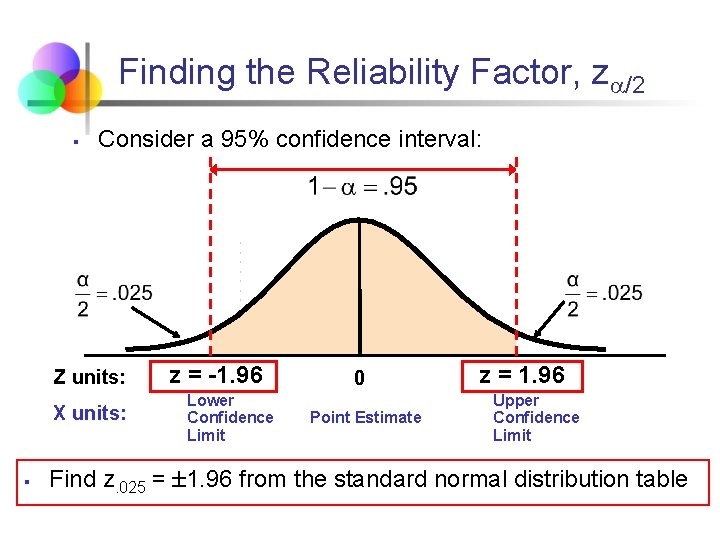
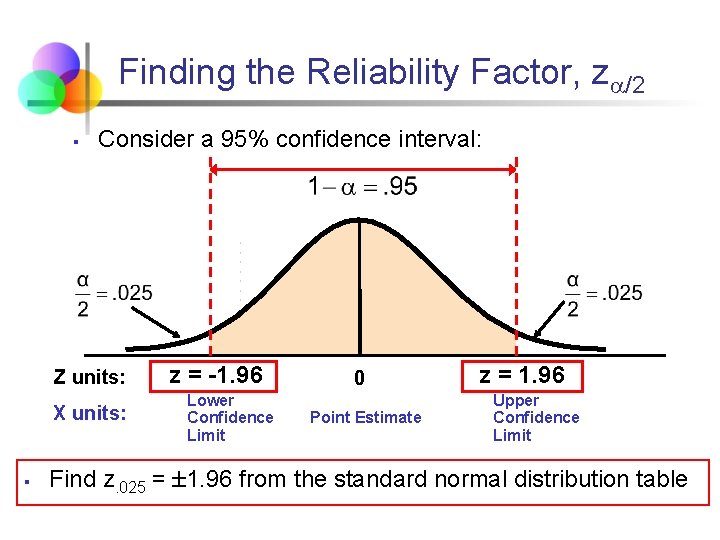
Finding the Reliability Factor, z /2 § Consider a 95% confidence interval: Z units: X units: § z = -1. 96 Lower Confidence Limit 0 Point Estimate z = 1. 96 Upper Confidence Limit Find z. 025 = 1. 96 from the standard normal distribution table

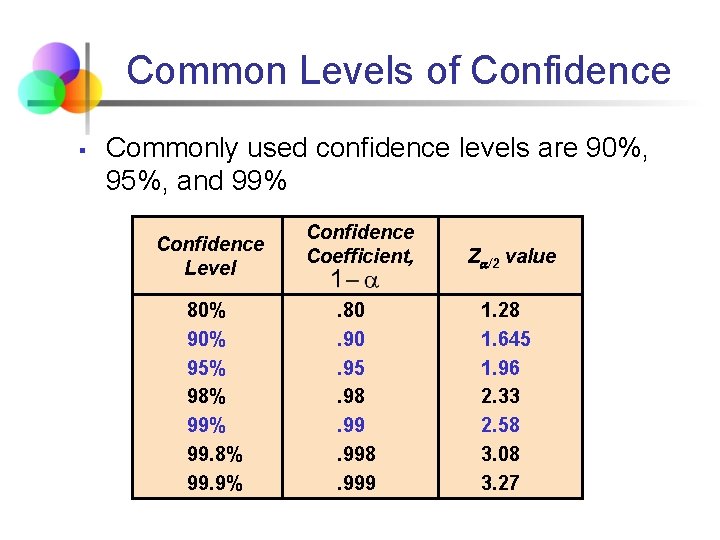
Common Levels of Confidence § Commonly used confidence levels are 90%, 95%, and 99% Confidence Level 80% 95% 98% 99. 9% Confidence Coefficient, Z /2 value . 80. 95. 98. 998. 999 1. 28 1. 645 1. 96 2. 33 2. 58 3. 08 3. 27

Intervals and Level of Confidence Sampling Distribution of the Mean x Intervals extend from x 1 x 2 to 100(1 - )% of intervals constructed contain μ; 100( )% do not. Confidence Intervals

Summary: Finding a confidence interval for μ (σ known) § Choose confidence level 1 -α (e. g. . 95). Find an interval [a, b] such that P(a<μ<b)=1 -α. a and b are determined by § How to find zα/2? § § Look in table for value such that P(Z> zα/2)=α e. g. if 1 -α=. 95, then zα/2 = 1. 96.

Finding the Reliability Factor, z /2 § Consider a 95% confidence interval: Z units: X units: § z = -1. 96 Lower Confidence Limit 0 Point Estimate z = 1. 96 Upper Confidence Limit Find z. 025 = 1. 96 from the standard normal distribution table

Example § § § Assume that the calorie contents per 100 ml of Guiness is normally distributed. A sample of 11 pints has a mean calorie content per 100 ml of 35. 1. We know from past testing that the population standard deviation is 2. 35. Determine a 95% confidence interval for the true mean calorie content per 100 ml Guiness.

Example (continued) § § A sample of 11 pints from a large normal population has a mean calorie content per 100 ml of 35. 1. We know from past testing that the population standard deviation is 2. 35 calories per 100 ml. Solution:

Interpretation § § We are 95% confident that the true calorie content per 100 ml is between 33. 7112 and 36. 4888. Although the true mean may or may not be in this interval, 95% of intervals formed in this manner will contain the true mean

Example § § Suppose a second sample of 11 pints has a mean calorie content per 100 ml of 35. 9. A 95% confidence interval for this sample is:

Reducing the Margin of Error The margin of error can be reduced if § the population standard deviation can be reduced (σ↓) § The sample size is increased (n↑) § The confidence level is decreased, (1 – ) ↓

How is the formula obtained? § § Recall the formula for the confidence interval: How is it obtained? A 100(1 -α)% confidence interval is an interval [a, b] such that P(a<μ<b) = 1 -α. We use the fact that

Derivation

Large Samples § § § If the population is not normal. . . . and the variance is not known. . The same confidence interval can still be used. . . if the sample is large. For in that case the Central Limit Theorem tells us that the sample mean is approximately normal with mean μ and standard deviation σ/√n, . . . and s 2 ≈ σ2.

Example § § § For a sample of 200 tea boxes you observe that the average weight is 101. 0 grams with a standard deviation of 2. 78 grams. Determine a 99% confidence interval for the population mean. Solution. Note that the sample is large, so: § § σ2 ≈ s 2 the Central Limit Theorem says that the sample mean is approximately normal with mean μ and standard deviation σ/√n≈2. 78/√ 200=. 197

Example § § So, we can proceed as if the sample mean is normal with known variance and apply Therefore:

Confidence Intervals Population Mean σ2 Known Population Proportion σ2 Unknown Population Variance

Confidence Interval for μ (σ2 Unknown) § § § If the population standard deviation σ is unknown, we can substitute the sample standard deviation, s This introduces extra uncertainty, since s is variable from sample to sample Therefore we use the t distribution instead of the normal distribution

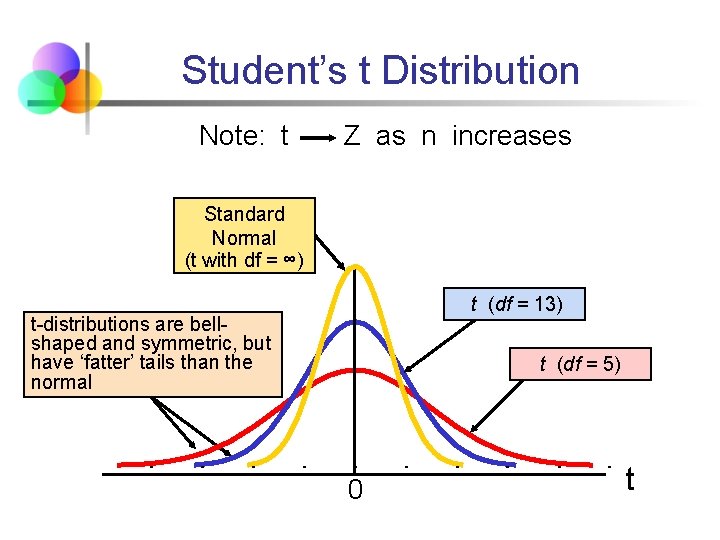
Student’s t Distribution § § Consider a random sample of n observations § with mean x and standard deviation s § from a normally distributed population with mean μ Then the variable follows the Student’s t distribution with (n - 1) degrees of freedom

Student’s t Distribution § § The t is a family of distributions The t-value depends on degrees of freedom (d. f. ) § Number of observations that are free to vary after sample mean has been calculated d. f. = n - 1

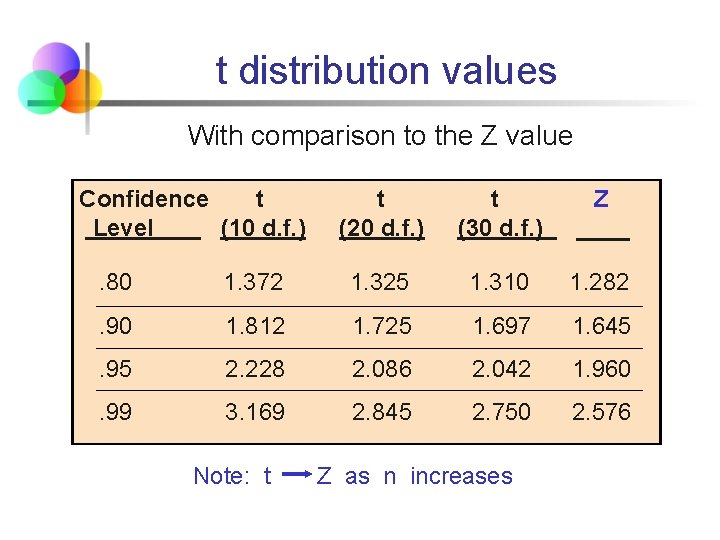
Student’s t Distribution Note: t Z as n increases Standard Normal (t with df = ∞) t (df = 13) t-distributions are bellshaped and symmetric, but have ‘fatter’ tails than the normal t (df = 5) 0 t

Confidence Interval for μ (σ Unknown) (continued) § Assumptions § § Population standard deviation is unknown Population is normally distributed Use Student’s t Distribution Confidence Interval Estimate: where tn-1, α/2 is the critical value of the t distribution with n-1 d. f. and an area of α/2 in each tail:

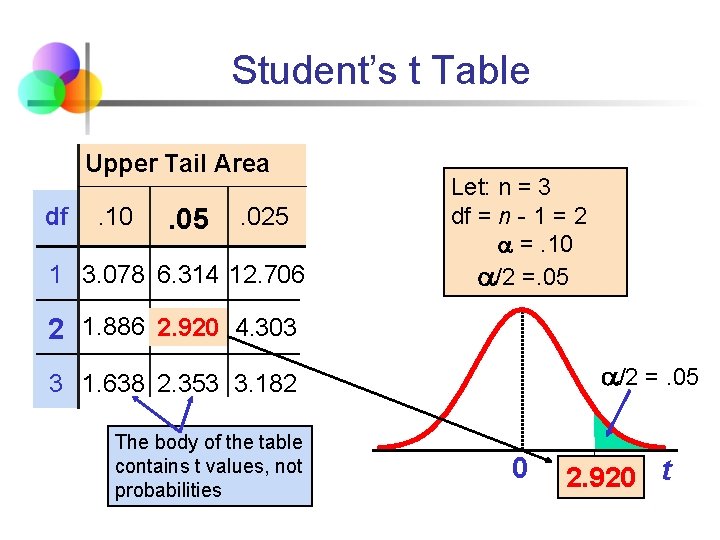
Student’s t Table Upper Tail Area df . 10 . 05 . 025 1 3. 078 6. 314 12. 706 Let: n = 3 df = n - 1 = 2 =. 10 /2 =. 05 2 1. 886 2. 920 4. 303 /2 =. 05 3 1. 638 2. 353 3. 182 The body of the table contains t values, not probabilities 0 2. 920 t

t distribution values With comparison to the Z value Confidence t Level (10 d. f. ) t (20 d. f. ) t (30 d. f. ) Z ____ . 80 1. 372 1. 325 1. 310 1. 282 . 90 1. 812 1. 725 1. 697 1. 645 . 95 2. 228 2. 086 2. 042 1. 960 . 99 3. 169 2. 845 2. 750 2. 576 Note: t Z as n increases

Example § § A sample of 11 pints has a mean calorie content per 100 ml of 35. 1, with a standard deviation of 2. 35. Determine a 95% confidence interval for the true mean calorie content per 100 ml Guiness if the calorie content is normal.

Example (continued) § § A sample of 11 pints from a large normal population has a mean calorie content per 100 ml of 35. 1, with a standard deviation of 2. 35 calories per 100 ml. Solution:

Interpretation § § We are 95% confident that the true calorie content per 100 ml is between 33. 5213 and 36. 6787. Compare with the previous example (variance known). . . where we were 95% confident that the true calorie content per 100 ml is between 33. 7112 and 36. 4888. The interval is wider because there is additional uncertainty over σ.

About Student § § Student is the pseudonym of William Sealy Gosset. . . who worked for the Guiness brewery in Dublin. . . and needed procedures for quality control of the brewing process. He derived the distribution of which is still named after him

Confidence Intervals Population Mean σ2 Known Population Proportion σ2 Unknown Population Variance

Confidence Intervals for the Population Proportion, p § § An interval estimate for the population proportion ( p ) can be calculated by adding an allowance for uncertainty to the sample proportion ( ) Sample has to be large because we will use the normal approximation to the binomial

Confidence Intervals for the Population Proportion, p (continued) § § Recall that the distribution of the sample proportion is approximately normal if the sample size is large, with standard deviation We will estimate this with sample data:

Confidence Interval Endpoints § § Upper and lower confidence limits for the population proportion are calculated with the formula where § § § z /2 is the standard normal value for the level of confidence desired is the sample proportion n is the sample size

Example § § A random sample of 100 people shows that 25 are left-handed. Form a 95% confidence interval for the true proportion of left-handers

Example (continued) § A random sample of 100 people shows that 25 are left-handed. Form a 95% confidence interval for the true proportion of left-handers.

Interpretation § § We are 95% confident that the true percentage of left-handers in the population is between 16. 51% and 33. 49%. Although the interval from 0. 1651 to 0. 3349 may or may not contain the true proportion, 95% of intervals formed from samples of size 100 in this manner will contain the true proportion.

General Example § § § Trinity news, Issue 9, vol. 54 reports the results of a poll with 430 respondents on the SU president election. It is reported that: “Moore [has] the slightest lead of 31. 7% to [. . . ] Donohue’s 29. 2% [. . . ] and Reilly’s 27. 2%. Given the margin of error the narrow gap [. . . ] means any one [can win]”. Compute a 95% confidence interval for the proportion of votes for Moore. What do you think about the paper’s claim referring to the margin of error?

First question § § § We have a large sample: n = 430 We are asked to compute a 95% confidence level: 1 -α=. 95 and – thus – α=. 05. The quantity of interest is a population proportion. Let p denote the proportion of votes for Moore. So, the appropriate confidence interval is

Obtain necessary info and apply Sample proportion: Use Table 1 or 8 to find So: We are 95% confident that the true poportion of votes for Moore is between 27. 3% and 36. 1%

Second question We are 95% confident that the true poportion of votes for Moore is between 27. 3% and 36. 1% The score for Donohue is 29. 2% and lies inside this 95% confidence interval, Reilly’s 27. 2%, however, does not. So, given the chosen level of confidence and the resulting margin of error, the race could be deemed “too close to call” between Moore and Donohue. NB The article does not specify the confidence level. So, we don’t know what “margin of error” it refers to. Bad statistical practise.

Probability Question § § In a particular city, 20% of mobile phones are owned by people younger than 15. In addition, 52% of people with a mobile phone have a “Pay As You Talk” deal. Among those younger than 15, 12% have a “Pay As You Talk” deal. What is the probability that a randomly chosen mobile phone is “Pay As You Talk” and belongs to someone younger than 15?

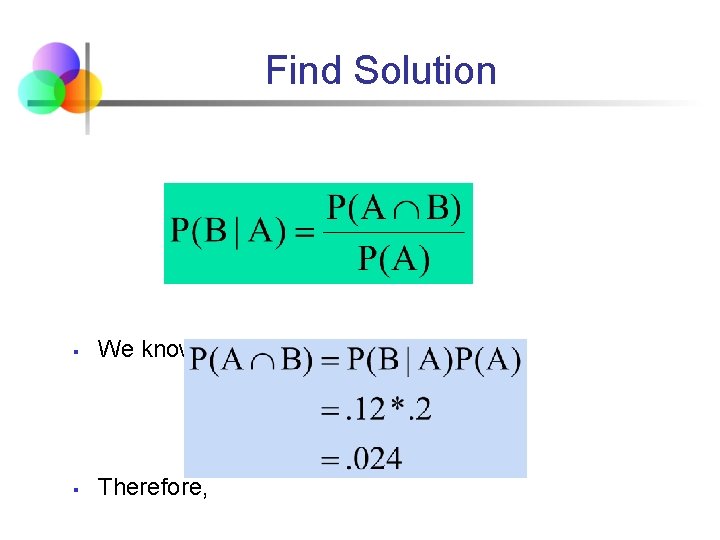
Set up the analysis § Give the events of interest a name: § § § What probabilties are given? § § Let A be the event that the phone belongs to a person younger than 15. Let B be the event that the phone is “Pay As You Talk” P(A) =. 2 P(B) =. 52 P(B|A) =. 12 What are we asked? § Joint probability of A and B: P(A∩B)

Find Solution § We know that: § Therefore,

Exam Tips § § Move on to next question if stuck Method more important than outcome § § § Write down all the steps you take § § don’t worry too much about rounding (not too many digits) computation errors have minor penalty avoids mistakes I can’t give marks if it’s not clear what you’re doing Before you answer a question think about your “plan of attack” before you start writing. Be relaxed when you walk in (no cramming).