Chapter 9 One and Two Sample Estimation Point

Chapter 9 One and Two Sample Estimation Point Estimates Unknown Parameter Symbol Point Estimator Population mean Symbol Sample mean m Population standard deviation Population proportion s Sample standard deviation Sample proportion s p Point estimates are computed from sample information and used to estimate population parameters. EGR 252 Ch. 9 Lecture 1 MDH 2015 9 th edition Slide 1

Interval Estimation q Interval estimation: The interval in which you would expect to find the value of a parameter. q By taking a random sample, we can compute an interval with upper and lower limits called a (1 -a) 100% confidence interval for the unknown parameter q In most a cases the parameter for intervals to be created will be m EGR 252 Ch. 9 Lecture 1 MDH 2015 9 th edition Slide 2

Confidence Intervals Point Estimates • Single value • Mean • Degree of uncertainty • Range of certainty around the point estimate Intervals • Point Estimates (mean) • Confidence level (1 -a) Based On • Standard deviation Expressed As • The mean score of the students was 80. 1 with a 95% CI of 77. 4 – 82. 5 EGR 252 Ch. 9 Lecture 1 MDH 2015 9 th edition Slide 3

Confidence Intervals q (1 – α) 100% confidence interval for the unknown parameter. Example: if α = 0. 01, we develop a 99% confidence interval. Ø Example: if α = 0. 05, we develop a 95% confidence interval. Ø EGR 252 Ch. 9 Lecture 1 MDH 2015 9 th edition Slide 4

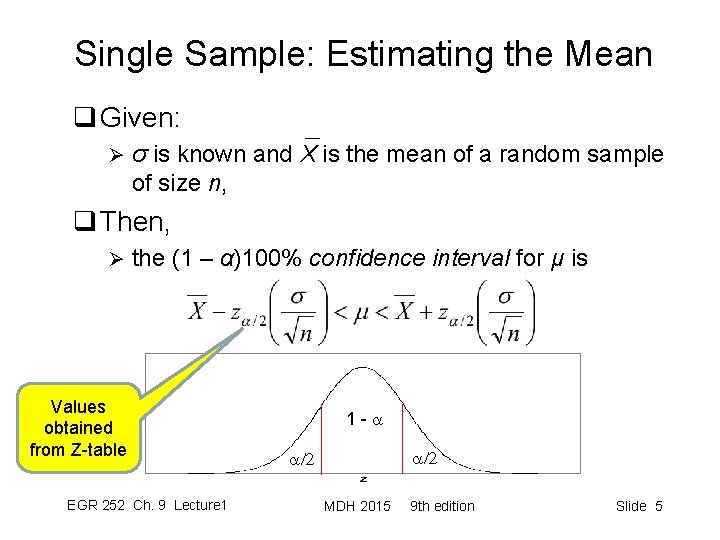
Single Sample: Estimating the Mean q Given: Ø σ is known and X is the mean of a random sample of size n, q Then, Ø the (1 – α)100% confidence interval for μ is Values obtained from Z-table EGR 252 Ch. 9 Lecture 1 1 - a a/2 MDH 2015 9 th edition Slide 5

Example A traffic engineer is concerned about the delays at an intersection near a local school. The intersection is equipped with a fully actuated (“demand”) traffic light and there have been complaints that traffic on the main street is subject to unacceptable delays. To develop a benchmark, the traffic engineer randomly samples 25 stop times (in seconds) on a weekend day. The average of these times is found to be 13. 2 seconds, and the variance is known to be 4 seconds 2. Based on this data, what is the 95% confidence interval (C. I. ) around the mean stop time during a weekend day? EGR 252 Ch. 9 Lecture 1 MDH 2015 9 th edition Slide 6

Example (cont. ) σ = ________ X = _______ α = ________ Z 0. 025 = _______ α/2 = _______ Z 0. 975 = ______ Enter values into equation EGR 252 Ch. 9 Lecture 1 MDH 2015 9 th edition Slide 7

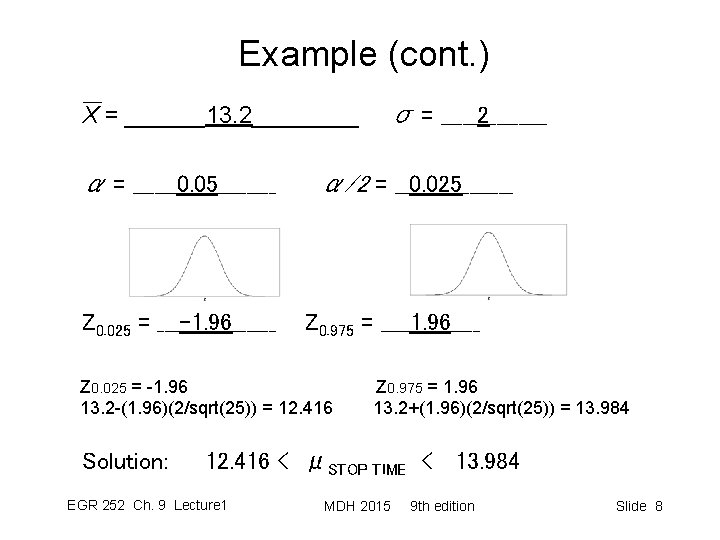
Example (cont. ) X = ______13. 2____ σ = _____2____ α = ______0. 05____ Z 0. 025 = ___-1. 96______ α/2 = __0. 025_______ Z 0. 975 = ____1. 96____ Z 0. 025 = -1. 96 Z 0. 975 = 1. 96 13. 2 -(1. 96)(2/sqrt(25)) = 12. 416 13. 2+(1. 96)(2/sqrt(25)) = 13. 984 Solution: 12. 416 < μSTOP TIME < 13. 984 EGR 252 Ch. 9 Lecture 1 MDH 2015 9 th edition Slide 8

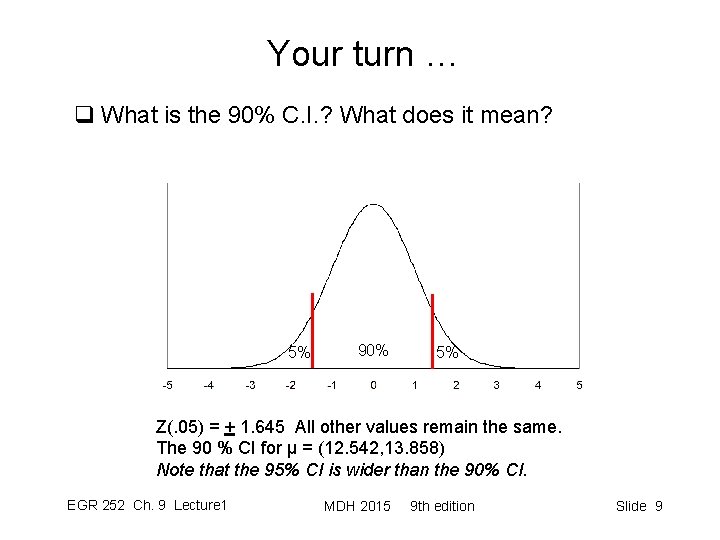
Your turn … q What is the 90% C. I. ? What does it mean? 5% 90% 5% Z(. 05) = + 1. 645 All other values remain the same. The 90 % CI for μ = (12. 542, 13. 858) Note that the 95% CI is wider than the 90% CI. EGR 252 Ch. 9 Lecture 1 MDH 2015 9 th edition Slide 9

What if σ 2 is unknown? q For example, what if the traffic engineer doesn’t know the variance of this population? 1. If n is sufficiently large (n > 30), then the large sample confidence interval is calculated by using the sample standard deviation in place of sigma: 2. If σ 2 is unknown and n is not “large”, we must use the t-statistic. EGR 252 Ch. 9 Lecture 1 MDH 2015 9 th edition Slide 10

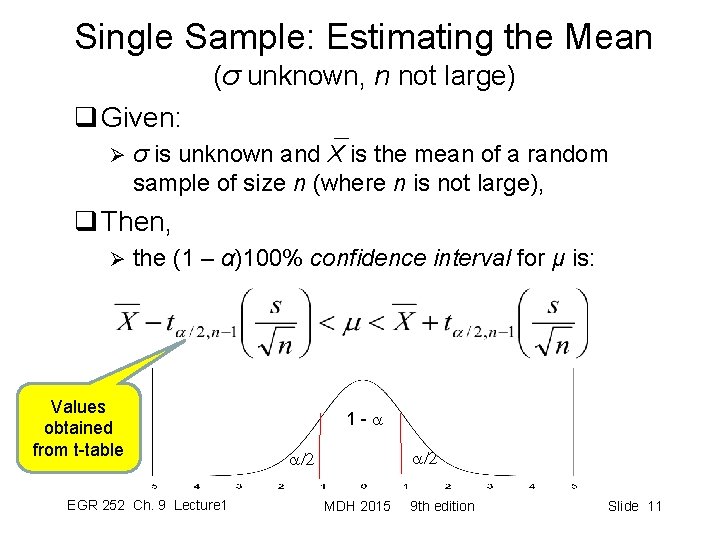
Single Sample: Estimating the Mean (σ unknown, n not large) q Given: Ø σ is unknown and X is the mean of a random sample of size n (where n is not large), q Then, Ø the (1 – α)100% confidence interval for μ is: Values obtained from t-table EGR 252 Ch. 9 Lecture 1 1 - a a/2 MDH 2015 9 th edition Slide 11

Recall Our Example A traffic engineer is concerned about the delays at an intersection near a local school. The intersection is equipped with a fully actuated (“demand”) traffic light and there have been complaints that traffic on the main street is subject to unacceptable delays. To develop a benchmark, the traffic engineer randomly samples 25 stop times (in seconds) on a weekend day. The average of these times is found to be 13. 2 seconds, and the sample variance, s 2, is found to be 4 seconds 2. Based on this data, what is the 95% confidence interval (C. I. ) around the mean stop time during a weekend day? EGR 252 Ch. 9 Lecture 1 MDH 2015 9 th edition Slide 12

Small Sample Example (cont. ) n = _______ v = _______ X = ______ s = _______ α/2 = ____ t 0. 025, 24 = _______ Find interval using equation below EGR 252 Ch. 9 Lecture 1 MDH 2015 9 th edition Slide 13

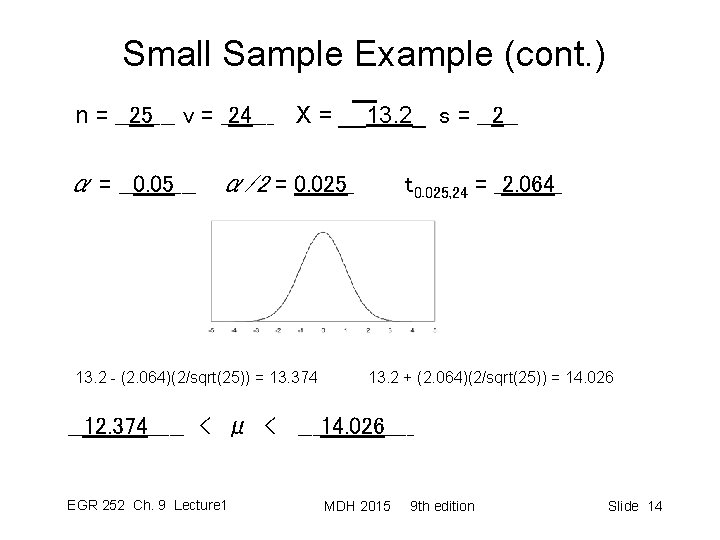
Small Sample Example (cont. ) n = __25___ v = _24___ X = __13. 2_ s = __2__ α = __0. 05___ α/2 = 0. 025_ 13. 2 - (2. 064)(2/sqrt(25)) = 13. 374 t 0. 025, 24 = _2. 064_ 13. 2 + (2. 064)(2/sqrt(25)) = 14. 026 __12. 374_____ < μ < ___14. 026____ EGR 252 Ch. 9 Lecture 1 MDH 2015 9 th edition Slide 14

Your turn A thermodynamics professor gave a physics pretest to a random sample of 15 students who enrolled in his course at a large state university. The sample mean was found to be 59. 81 and the sample standard deviation was 4. 94. Find a 99% confidence interval for the mean on this pretest. EGR 252 Ch. 9 Lecture 1 MDH 2015 9 th edition Slide 15

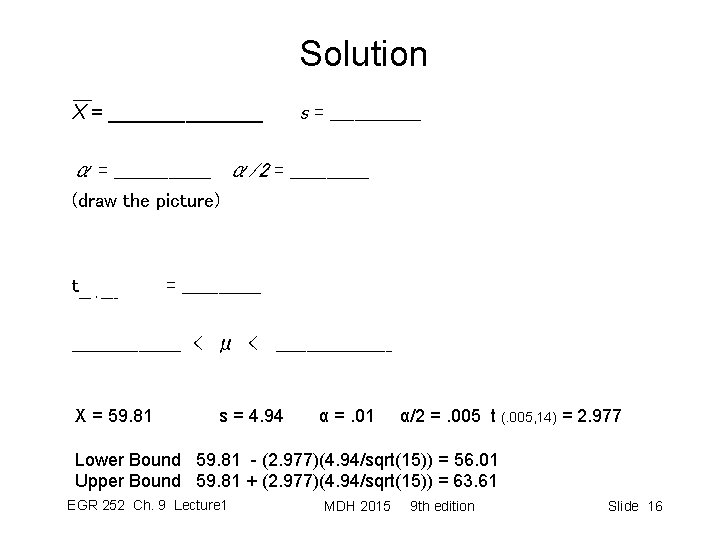
Solution X = _______ s = ________ α/2 = _______ (draw the picture) t___ , ____ = __________________ < μ < __________ X = 59. 81 s = 4. 94 α =. 01 α/2 =. 005 t (. 005, 14) = 2. 977 Lower Bound 59. 81 - (2. 977)(4. 94/sqrt(15)) = 56. 01 Upper Bound 59. 81 + (2. 977)(4. 94/sqrt(15)) = 63. 61 EGR 252 Ch. 9 Lecture 1 MDH 2015 9 th edition Slide 16

Standard Error of a Point Estimate q Case 1: σ known Ø The standard deviation, or standard error of X is q Case 2: σ unknown, sampling from a normal distribution Ø The standard deviation, or (usually) estimated standard error of X is EGR 252 Ch. 9 Lecture 1 MDH 2015 9 th edition Slide 17

Prediction Intervals q Used to predict the possible value of a future observation q Example: In quality control, an experimenter may need to use the observed data to predict a new observation. EGR 252 Ch. 9 Lecture 1 MDH 2015 9 th edition Slide 18

9. 6: Prediction Interval q For a normal distribution of unknown mean μ, and standard deviation σ, a 100(1 -α)% prediction interval of a future observation, x 0 is if σ is known, and if σ is unknown EGR 252 Ch. 9 Lecture 1 MDH 2015 9 th edition Slide 19

Tolerance Limits (Intervals) q What if you want to be 95% sure that the interval contains 95% of the values? Or 90% sure that the interval contains 99% of the values? q These questions are answered by a tolerance interval. To compute, or understand, a tolerance interval you have to specify two different percentages. One expresses how sure you want to be, and the other expresses what fraction of the values the interval will contain. EGR 252 Ch. 9 Lecture 1 MDH 2015 9 th edition Slide 20

9. 7: Tolerance Limits q For a normal distribution of unknown mean μ, and unknown standard deviation σ, tolerance limits are given by x + ks where k is determined so that one can assert with 100(1 -γ)% confidence that the given limits contain at least the proportion 1 -α of the measurements. q Table A. 7 (page 745) gives values of k for (1 -α) = 0. 9, 0. 95, or 0. 99 and γ = 0. 05 or 0. 01 for selected values of n. EGR 252 Ch. 9 Lecture 1 MDH 2015 9 th edition Slide 21

Tolerance Limits q How to determine 100(1 -γ)% and 1 -α. For a sample size of 8, find the tolerance interval that gives two-sided 95% bounds on 90% of the distribution or population. X is 15. 6 and s is 1. 4 1 -g (boundary or the limits) 1 -a (proportion of the distribution) From table on pg. 745, find the corresponding value: n = 8, g =. 05, a = 0. 1 corresponding k…k = 3. 136 x + ks = 15. 6 + (3. 136)(1. 4) Tolerance interval 19. 99 – 11. 21 We are 95% confident that 90% of the population falls within the limits of 11. 21 and 19. 99 EGR 252 Ch. 9 Lecture 1 MDH 2015 9 th edition Slide 22

Case Study 9. 1 c (Page 281) q Find the 99% tolerance limits that will contain 95% of the metal pieces produced by the machine, given a sample mean diameter of 1. 0056 cm and a sample standard deviation of 0. 0246. q Table A. 7 (page 745) Ø Ø Ø (1 - α ) = 0. 95 (1 – Ƴ ) = 0. 99 n=9 k = 4. 550 x ± ks = 1. 0056 ± (4. 550) (0. 0246) q We can assert with 99% confidence that the tolerance interval from 0. 894 to 1. 117 cm will contain 95% of the metal pieces produced by the machine. EGR 252 Ch. 9 Lecture 1 MDH 2015 9 th edition Slide 23

Summary Confidence interval population mean μ Prediction interval a new observation x 0 Tolerance interval a (1 -α) proportion of the measurements can be estimated with 100( 1 -Ƴ )% confidence EGR 252 Ch. 9 Lecture 1 MDH 2015 9 th edition Slide 24