VEDIC MATHEMATICS What is vedic mathematics Vedic Mathematics

VEDIC MATHEMATICS

What is vedic mathematics ? • Vedic Mathematics is the name given to the ancient system of Mathematics which was rediscovered from the Vedas between 1911 and 1918 by Sri Bharati Krsna Tirthaji (1884 -1960). According to his research all of mathematics is based on sixteen Sutras or wordformulae. For example, 'Vertically and Crosswise` is one of these Sutras. These formulae describe the way the mind naturally works and are therefore a great help in directing the student to the appropriate method of solution.

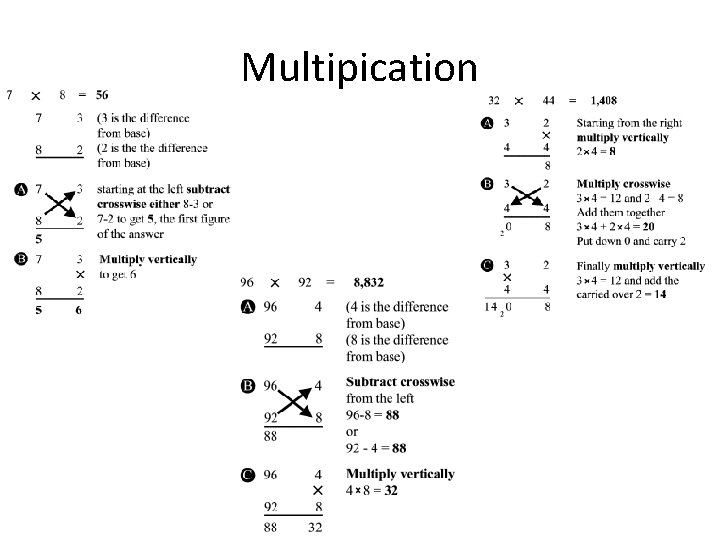
Multipication

• • Method explaination The sutra "vertically and crosswise" has many uses. One very useful application is helping children who are having trouble with their tables above 5 x 5. For example 7 x 8. 7 is 3 below the base of 10, and 8 is 2 below the base of 10. The whole approach of Vedic maths is suitable for slow learners, as it is so simple and easy to use. The sutra "vertically and crosswise" is often used in long multiplication. Suppose we wish to multiply 32 by 44. We multiply vertically 2 x 4=8. Then we multiply crosswise and add the two results: 3 x 4+4 x 2=20, so put down 0 and carry 2. Finally we multiply vertically 3 x 4=12 and add the carried 2 =14. Result: 1, 408. We can extend this method to deal with long multiplication of numbers of any size. The great advantage of this system is that the answer can be obtained in one line and mentally. By the end of Year 8, I would expect all students to be able to do a "3 by 2" long multiplication in their heads. This gives enormous confidence to the pupils who lose their fear of numbers and go on to tackle harder maths in a more open manner. All the techniques produce one-line answers and most can be dealt with mentally, so calculators are not used until Year 10. The methods are either "special", in that they only apply under certain conditions, or general. This encourages flexibility and innovation on the part of the students. Multiplication can also be carried out starting from the left, which can be better because we write and pronounce numbers from left to right. Here is an example of doing this in a special method for long multiplication of numbers near a base (10, 100, 1, 000 etc), for example, 96 by 92. 96 is 4 below the base and 92 is 8 below. We can cross-subtract either way: 96 -8=88 or 92 -4=88. This is the first part of the answer and multiplying the "differences" vertically 4 x 8=32 gives the second part of the answer.

Addition • In the convention process we perform the process as follows. 234 + 403 + 564 + 721 write as 234 403 564 721 • Step (i): 4 + 3 + 4 + 1 = 12 2 retained and 1 is carried over to left. Step (ii): 3 + 0 + 6 + 2 = 11 the carried ‘ 1’ is added i. e. , Now 2 retained as digit in the second place (from right to left) of the answer and 1 is carried over to left. step (iii): 2 + 4 + 5 + 7 = 18 carried over ‘ 1’ is added i. e. , 18 + 1 = 19. As the addition process ends, the same 19 is retained in the left had most part of the answer. thus 234 403 564 +721 and 1922 is the answer