ALTERNATING SERIES series with positive terms series with





















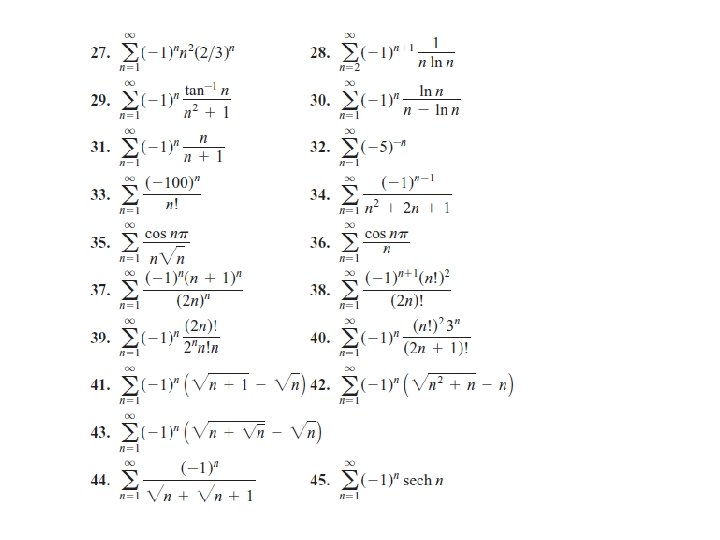








- Slides: 35

ALTERNATING SERIES series with positive terms series with some positive and some negative terms alternating series n-th term of the series are positive

ALTERNATING SERIES alternating series alternating harmonic series alternating geomtric series alternating p-series

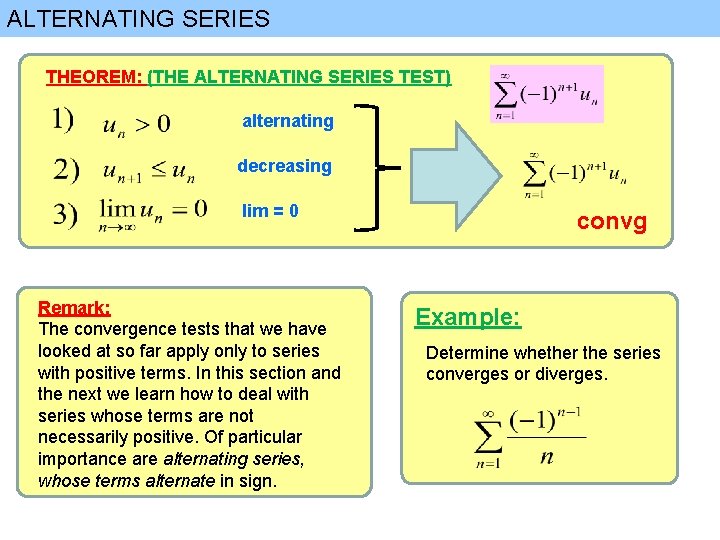
ALTERNATING SERIES THEOREM: (THE ALTERNATING SERIES TEST) alternating decreasing lim = 0 Remark: The convergence tests that we have looked at so far apply only to series with positive terms. In this section and the next we learn how to deal with series whose terms are not necessarily positive. Of particular importance are alternating series, whose terms alternate in sign. convg Example: Determine whether the series converges or diverges.

ALTERNATING SERIES THEOREM: (THE ALTERNATING SERIES TEST) alternating decreasing lim = 0 Example: Determine whether the series converges or diverges. convg

ALTERNATING SERIES THEOREM: (THE ALTERNATING SERIES TEST) alternating decreasing lim = 0 Example: Determine whether the series converges or diverges. convg

ALTERNATING SERIES THEOREM: (THE ALTERNATING SERIES ESTIMATION THEOREM) satisfies the three conditions approximates the sum L of the series with an error whose absolute value is less than the absolute value of the first unused term the sum L lies between any two successive partial sums and the remainder, has the same sign as the first unused term. OR Example:

ALTERNATING SERIES THEOREM: (THE ALTERNATING SERIES ESTIMATION THEOREM) satisfies the three conditions OR Example: Find the sum of the series correct to three decimal places.

ALTERNATING SERIES Example: Find the sum of the series correct to three decimal places.

ALTERNATING SERIES THEOREM: (THE ALTERNATING SERIES ESTIMATION THEOREM) satisfies the three conditions OR REMARK: The rule that the error is smaller than the first unused term is, in general, valid only for alternating series that satisfy the conditions of the Alternating Series Estimation Theorem. The rule does not apply to other types of series.

ALTERNATING SERIES TERM-102

ALTERNATING SERIES TERM-101

ALTERNATING SERIES TERM-092

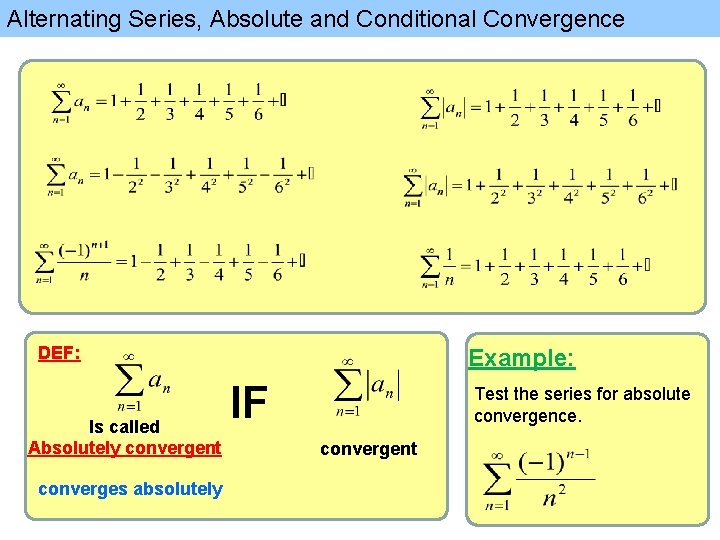
Alternating Series, Absolute and Conditional Convergence DEF: Is called Absolutely convergent converges absolutely Example: IF Test the series for absolute convergence. convergent

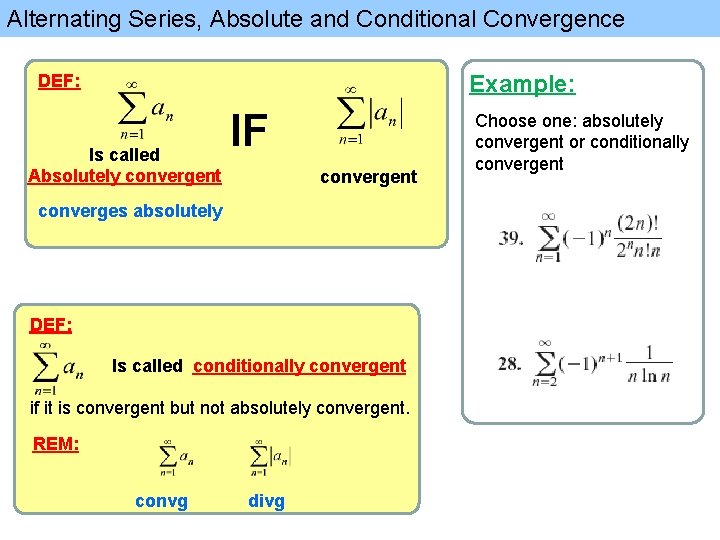
Alternating Series, Absolute and Conditional Convergence DEF: Example: Is called Absolutely convergent IF Test the series for absolute convergence. convergent converges absolutely DEF: Example: Is called conditionally convergent if it is convergent but not absolutely convergent. REM: convg divg Test the series for absolute convergence.

Alternating Series, Absolute and Conditional Convergence Example: DEF: Is called Absolutely convergent IF Test the series for absolute convergence. convergent converges absolutely DEF: Is called conditionally convergent if it is convergent but not absolutely convergent. REM: convg divg

Alternating Series, Absolute and Conditional Convergence THM: Absolutely convergent THM: convg Example: Determine whether the series converges or diverges.

Alternating Series, Absolute and Conditional Convergence conditionally convergent Absolutely convergent divergent

Alternating Series, Absolute and Conditional Convergence Example: DEF: Is called Absolutely convergent IF convergent converges absolutely DEF: Is called conditionally convergent if it is convergent but not absolutely convergent. REM: convg divg Choose one: absolutely convergent or conditionally convergent

Alternating Series, Absolute and Conditional Convergence REARRANGEMENTS Divergent If we rearrange the order of the terms in a finite sum, then of course the value of the sum remains unchanged. But this is not always the case for an infinite series. By a rearrangement of an infinite series we mean a series obtained by simply changing the order of the terms.

Alternating Series, Absolute and Conditional Convergence REARRANGEMENTS Divergent convergent See page 719

Alternating Series, Absolute and Conditional Convergence REARRANGEMENTS REMARK: Absolutely convergent any rearrangement has the same sum s with sum s Riemann proved that Conditionally convergent r is any real number there is a rearrangement that has a sum equal to r.

SUMMARY OF TESTS

SUMMARY OF TESTS Series Tests Special Series: 1) Test for Divergence 1) Geometric Series 2) Integral Test 2) Harmonic Series 3) Comparison Test 3) Telescoping Series 4) Limit Comparison Test 4) p-series 5) Ratio Test 5) Alternating p-series 6) Root Test 7) Alternating Series Test

SUMMARY OF TESTS 1) Determine whether convg or divg 2) Find the sum s 5 -types 3) Estimate the sum s 5) Partial sums 4) How many terms are needed within error


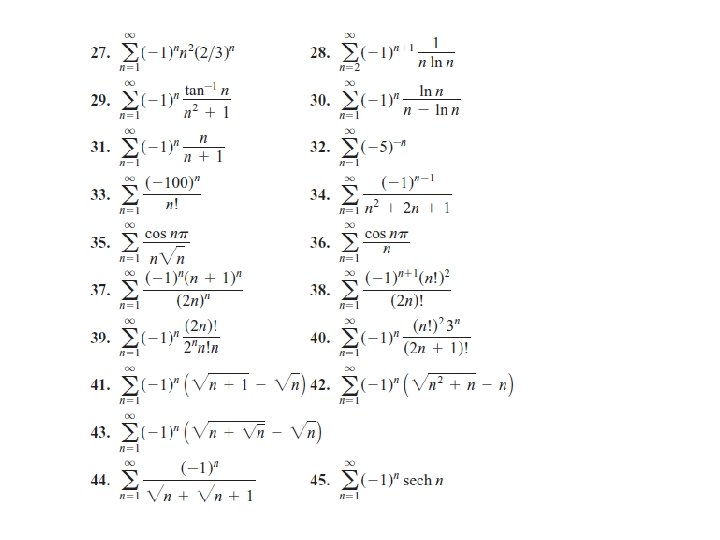








ALTERNATING SERIES TERM-101