Statistical inference point and interval estimate Statistical Inference









































- Slides: 47

Statistical inference: point and interval estimate

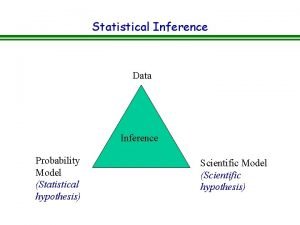
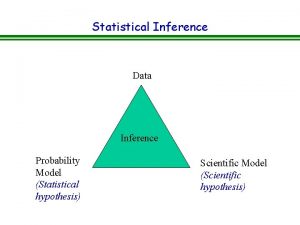
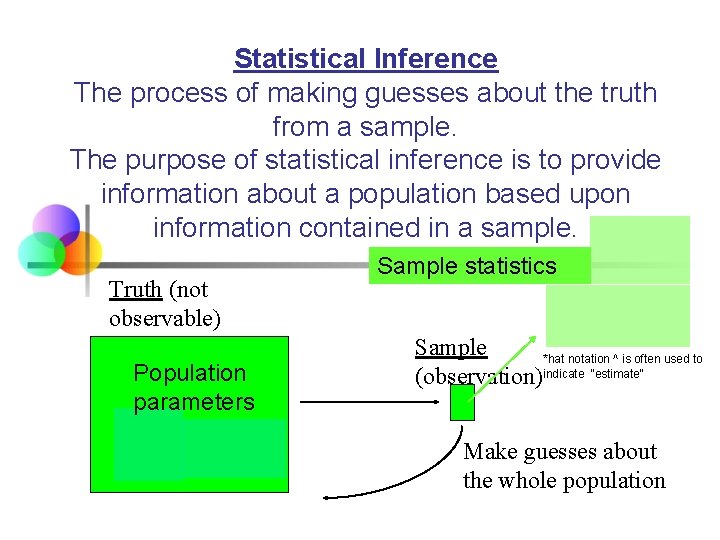
Statistical Inference The process of making guesses about the truth from a sample. The purpose of statistical inference is to provide information about a population based upon information contained in a sample. Truth (not observable) Population parameters Sample statistics Sample *hat notation ^ is often used to (observation)indicate “estimate” Make guesses about the whole population

Statistical inference n The reasons to make guesses about the whole population based on sample statistics: Contacting the entire population is too time consuming. n The cost of studying all the items in the population is often too expensive. n The sample results are usually adequate. n The destructive nature of certain tests. n The physical impossibility of checking all items. As we mentioned before, there are several methods of sampling (simple random sample is the most widely used method, others are: systematic sampling, stratified sampling, and cluster sampling). n

Inferential statistics (or Statistical inference) n n Assume that we are working with the sample and we calculate a sample statistics such: sample average, sample variance, sample standard deviation. Based on the sample we assume the properties of a population. This means , the values of a sample statistics are used to estimate the unknown values of population parameters. Usually we estimate parameters of population such : population mean, population variance, standard deviation of population. 4

Statistics vs. Parameters n n A population – is the collection of all elements of interest. Population parameter – the true value/true effect in the entire population of interest. n n n E. g. , the true mean vitamin D level in all middle-aged and older European men is 62 nmol/L. A sample – is a subset of a population. Sample Statistic – any summary measure calculated from data; e. g. , could be a mean. n E. g. , the mean vitamin D level in a sample of 100 men is 63 nmol/L.

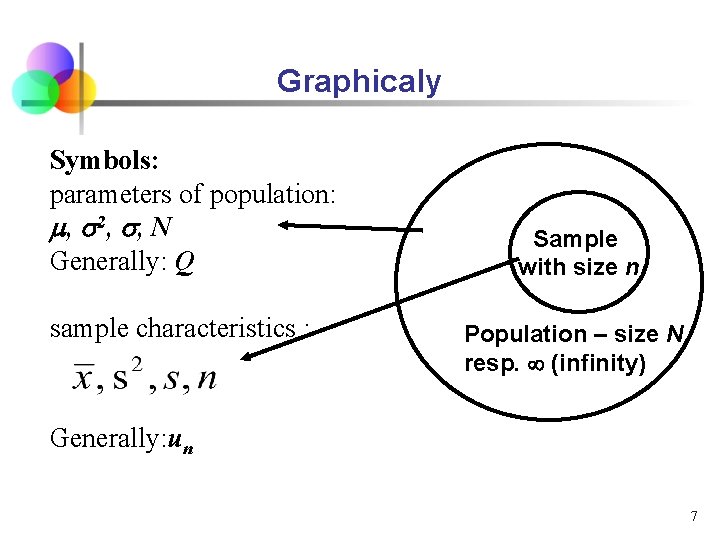
Symbols: PARAMETERS OF POPULATION SAMPLE STATISTICS N – size of population - population mean n - sample size s – sample standard deviation Q – population in general

Graphicaly Symbols: parameters of population: , 2, , N Generally: Q sample characteristics : Sample with size n Population – size N, resp. (infinity) Generally: un 7

What we have accomplished with sampling distributions • Given a population parameter, we know that a sample statistic will produce a better estimate of the population parameter when the sample is larger (better means more accurate and normally distributed). 8

Estimation - Definitions • Point estimate: a single statistics, computed from sample information, which is used to estimate the population parameter. • Point estimator: the equation used to produce the point estimate. • Interval estimate: a range of numbers around the point estimate within which the parameter is believed to fall. Also called a confidence interval. 9

Mathematical Theory… The Central Limit Theorem! If all possible random samples, each of size n, are taken from any population with a mean and a standard deviation , the sampling distribution of the sample means (averages) will: 1. have mean: 2. have standard deviation: 3. be approximately normally distributed regardless of the shape of the parent population (normality improves with larger n).

Symbol Check The mean of the sample means. The standard deviation of the sample means. Also called “the standard error of the mean. ”

The Central Limit Theorem n

The Central Limit Theorem n

The basics of point estimation • The typical point estimator of a population mean is a sample mean: • The typical point estimator of a population variance is a sample variance: • The typical point estimator of a population standard deviation is a sample standard deviation: 14

Typical point estimator for standard errors • Estimated standard error of samples drawn from a population: 15

Choosing a good estimator You can technically use any equation you want as a point estimator, but the most popular ones have certain desirable properties. • Unbiasedness: The sampling distribution for the estimator ‘centers’ around the parameter (on average, the estimator gives the correct value for the parameter). • Efficiency: If at the sample size one unbiased estimator has a smaller sampling error than another unbiased estimator, the first one is more efficient. • Consistency: The value of the estimator gets closer to the parameter as sample size increases. Consistent estimators may be biased, but the bias must become smaller as the sample size increases if the consistency property holds true. 16

Examples for point estimates: Given the following sample of seven observations: 5, 2, 4, 5, 5 • • What is the estimator of the population mean? What is the estimate of the population mean? What is the estimator of the population variance? What is the estimate of the population variance? What is the estimator of the population standard deviation? What is the estimate of the population standard error for this sample? 17

Examples for point estimates: Given the following sample of seven observations: 5, 2, 4, 5, 5 n What is the estimator of the population mean? n What is the estimate of the population mean? (5+2+4+5+5) / 7 = 28 / 7 = 4 n What is the estimator of the population variance? n What is the estimate of the population variance? [(5 -4)2+(2 -4)2+(4 -4)2+(5 -4)2]/6=2 18

Examples for point estimates:

Exercise: 1. The following data have been collected from a simple random sample. 5 8 10 7 10 14 a) What is the point estimate of the population mean? b) What is the point estimate of the population standard deviation? 2. A simple random sample of 5 months of sales data provided the following: Month Units Sold 1 2 3 4 5 94 100 85 94 92 a) What is the point estimate of the population mean number of units sold per month? b) What is the point estimate of the population standard deviation?

Point estimate vs. Interval estimates Point estimate– we use when it is necessary that one particular number is the estimate of the parameter. The point estimate of the population parameter provides an unbiasedness, efficiency and consistency estimate, but we cannot determine the sampling error. The point estimate is therefore only used as a basis for interval estimates and statistical hypothesis testing.

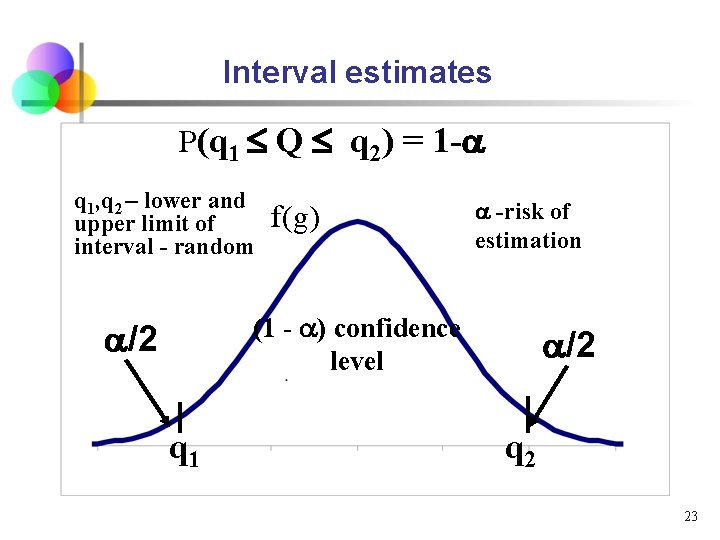
Interval estimates Interval estimate of the population parameter Q: • Where: estimated population parameter Q is located in the interval (q 1, q 2) with probability 1 -a • interval (q 1, q 2) = confidence interval and it is depending on a • a - indicates the probability that parameter Q does not belong into the confidence interval - risk of estimation • the probability 1 -a then says that the parameter Q is from the interval (q 1, q 2) and is called the confidence coefficient, respectively estimation reliability

Interval estimates P(q 1 Q q 2) = 1 - q 1, q 2 – lower and upper limit of interval - random f(g) -risk of estimation (1 - ) confidence level /2 q 1 /2 q 2 23

Interval estimates • Interval estimate (also called a confidence interval): a range of numbers that we think has a given probability of containing a parameter. • Confidence coefficient: The probability that the interval estimate contains the parameter. Typical confidence coefficients are 1 -a = 0. 95 and 0. 99. = 24

Interval estimates • with increasing the confidence coefficient, the confidence interval is also increasing and at the same time the accurency of the estimation is decreasing • with decreasing the confidence coefficient, the confidence interval is also decreasing and at the same time the risk of estimation is increasing • the basis of the interval etimations is: • estimation of the characteristic un • determination of distribution un

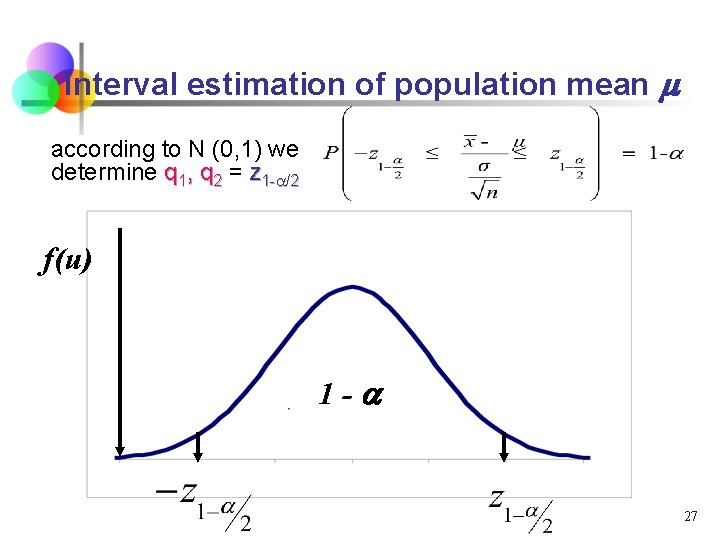
Interval estimation of population mean n n Suppose that the population parameter Q has a normal distribution - N( , 2) If we will create a sample with size n, then also sample statistic has a normal distribution Confidence interval for depends on disponibility of information and sample size: a) If the variance of population is known (theoretical assumption) we can create standardized normal variable: z (u) has N(0, 1) independent on estimated value 26

Interval estimation of population mean according to N (0, 1) we determine q 1, q 2 = z 1 -a/2 f(u) 1 - 27

Interval estimation of population mean After transformation we get following equation: - sampling error - half of the interval, determinates accurancy of the estimation, Interval estimate is actually point estimate , e. g. 28

Interval estimation of population mean b) The population variance is unknown est 2 = s 12 , and the sample size is large, n > 30 We can use N(0, 1) c) If the population variance is unknown est 2 = s 12 , and the sample size is small (less than 30), n 30 t (n-1) –critical value of Student’s distribution at alfa level and at degrees of freedom 29

Equations for interval estimates • Confidence interval of a mean • where… • and where you choose z, based on the p-value for the confidence interval you want • Assumption: the sample size is large enough that the sampling distribution is approximately normal 30

Notes on interval estimates • Usually, we are not given z. Instead we start with a desired confidence interval (e. g. , 95% confidence), and we select an appropriate z – score. • We generally use a 2 -tailed distribution in which ½ of the confidence interval is on each side of the sample mean. 31

Equations for interval estimates • Example: find c. i. when Ybar =10. 2, s=10. 1, N=1055, interval=95%. • z is derived from the 95% value: what value of z leaves 95% in the middle and 2. 5 % on each end of a distribution? • For p =. 975, z = 1. 96 • The standard error is s/SQRT(n) = 10. 1/SQRT(1055) =. 31095 • Top of the confidence interval is 10. 2 + 1. 96*. 31095 = 10. 8095 • The bottom of the interval is 10. 2 – 1. 96*. 31095 = 9. 5905 • Hence, the confidence interval is 9. 59 to 10. 81 32

Confidence Intervals in general The value of the statistic in my sample (eg. , mean, odds ratio, etc. ) point estimate (measure of how confident we want to be) (standard error) From a Z table or a T table, depending on the sampling distribution of the statistic. Standard error of the statistic.

Common “Z” levels of confidence n n Confidence levels and corresponding Z values: Commonly used confidence levels are 95% and 99% Confidence Level 80% 95% 98% 99. 9% Z value 1. 28 1. 645 1. 96 2. 33 2. 58 3. 08 3. 27

Confidence Interval for the Variance and Standard Deviation of a Normal Distribution

Summary

Important notes regarding confidence intervals n n The width of the confidence interval is related to the significance level, standard error, and n (number of observations) such that the following are true: the higher the percentage of accuracy (significance) desired, the wider the confidence interval the larger the standard error, the wider the confidence interval the larger the n, the smaller the standard error, and so the narrower the confidence interval

Important note regarding the sample size and sampling error n n n The lower the desired sampling error the larger the sample size must be. Note: Sampling error is influenced by: confidence level - we can influence the confidence level (sample) standard deviation - we can't influence the variability within the sample size - we can influence the sample size

Point estimate of mean n

Interval estimate of mean n

Interval estimate of mean n

Point estimate of variance n

Interval estimate of variance

Point estimate of standard deviation n

Interval estimate of standard deviation n

Calculating the sample size n

Next topic n Hypothesis testing Thank you! Have a nice day!
 Interval estimate example
Interval estimate example Nada cg berjarak
Nada cg berjarak Primary and secondary reinforcers
Primary and secondary reinforcers Fixed variable ratio interval
Fixed variable ratio interval Proof of chebyshev's inequality
Proof of chebyshev's inequality Probability and statistical inference 9th solution pdf
Probability and statistical inference 9th solution pdf Wecan95
Wecan95 How to find point estimate
How to find point estimate How to find point estimate
How to find point estimate How to find point estimate
How to find point estimate College board
College board What is the point estimate of μ?
What is the point estimate of μ? Point estimate
Point estimate Common critical values
Common critical values Is the point estimate the mean
Is the point estimate the mean Contoh soal estimasi interval kepercayaan
Contoh soal estimasi interval kepercayaan Point estimate equation
Point estimate equation Point estimate equation
Point estimate equation A point estimate consists of a single sample
A point estimate consists of a single sample Single value estimate
Single value estimate Point estimate
Point estimate Stat 211
Stat 211 Statistical inference
Statistical inference Statistical inference is concerned with
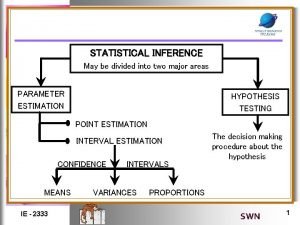
Statistical inference is concerned with Statistical inference is divided into
Statistical inference is divided into What are the 4 measurement scales?
What are the 4 measurement scales? Hub and-spoke system advantages and disadvantages
Hub and-spoke system advantages and disadvantages Estimate and rounding
Estimate and rounding Estimate fractions sums and differences
Estimate fractions sums and differences Trench excavation calculation
Trench excavation calculation Index notation
Index notation What is front end rounding with decimals
What is front end rounding with decimals 1-4 extrema and average rates of change
1-4 extrema and average rates of change Estimate and classify the extrema for the graph
Estimate and classify the extrema for the graph Horizontal answers
Horizontal answers Round the factors and estimate the products 656 x 106
Round the factors and estimate the products 656 x 106 Estimation of power wiring systems
Estimation of power wiring systems Point by point organization
Point by point organization Dew point and bubble point
Dew point and bubble point Points of parity and points of difference
Points of parity and points of difference City drawing easy
City drawing easy Congruent and incongruent melting point
Congruent and incongruent melting point Indicator end point
Indicator end point In metaphoric extension the novel stimulus shares
In metaphoric extension the novel stimulus shares Far point and near point
Far point and near point Far point and near point
Far point and near point Astm d6045
Astm d6045 The melting point of ice
The melting point of ice