MATEMATIKA DASAR I Dosen Asri Nur Chiquita Himpunan

MATEMATIKA DASAR I Dosen : Asri Nur Chiquita

Himpunan bilangan dan skemanya

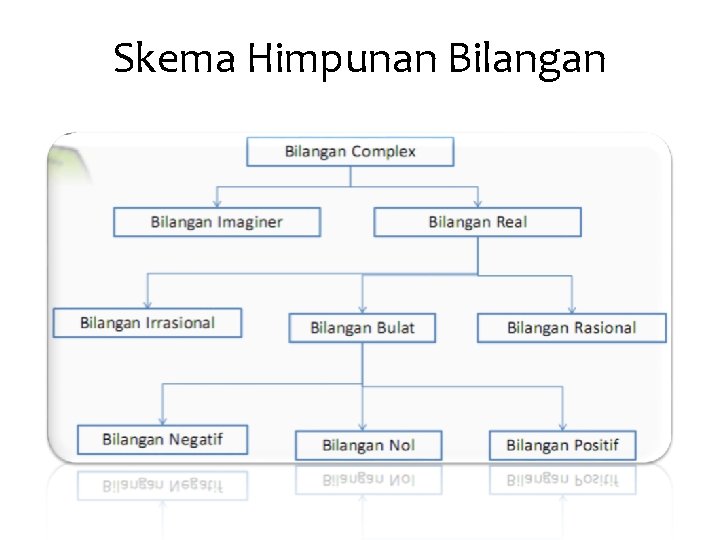
Skema Himpunan Bilangan

• Himpunan bilangan asli adalah himpunan bilangan yang anggotanya merupakan bilangan bulat positif. Ex: N = {1, 2, 3, 4, 5, 6, . . . } • Himpunan bilangan prima adalah himpunan bilangan-bilangan asli yang hanya dapat dibagi dirinya sendiri dan satu, kecuali angka 1. Ex: P = {2, 3, 5, 7, 11, 13, . . }

• Himpunan bilangan cacah adalah himpunan bilangan yang anggotanya merupakan bilangan bulat positif digabung dengan nol. Ex: C = {0, 1, 2, 3, 4, 5, 6, . . } • Himpunan bilangan bulat adalah himpunan bilangan yang anggotanya seluruh bilangan bulat, baik negatif, nol, dan positif. Ex: B = {. . . , -3, -2, -1, 0, 1, 2, 3, . . . }

• Himpunan bilangan rasional adalah himpunan bilangan yang anggota-anggonya merupakan bilangan yang dapat dinyatakan sebagai: p/q dimana p, q bulat dan q 0 atau dapat dinyatakan sebagai suatu desimal berulang. Contoh: 0, -2, 2/7, 5, 2/11, dan lain • Himpunan bilangan irasional adalah himpunan bilangan yang anggota-anggotanya tidak dapat dinyatakan sebagai p/q atau tidak dapat dinyatakan sebagai suatu desimal berulang. contoh: log 2, e, 7

• Himpunan bilangan riil adalah himpunan yang anggota-anggotanya merupakan gabungan dari himpunan bilangan rasional dan irasional. contoh: log 10, 5/8, -3, 0, 3 • Himpunan bilangan imajiner adalah himpunan bilangan yang anggota-anggotanya merupakan i (satuan imajiner) dimana i merupakan lambang bilangan baru. contoh: i, 4 i, 5 i

• Himpunan bilangan kompleks adalah himpunan bilangan yang anggotanya (a + bi) dimana a, b R, i² = -1, dengan a bagian riil dan b bagian imajiner. contoh: 2 -3 i, 8+2

Bilangan bulat

• Bilangan bulat adalah bilangan bukan pecahan yang terdiri dari bilangan : § Bulat positif (1, 2, 3, 4, 5, …) § Nol : 0 § Bulat Negatif ( …, -5, -4, -3, -2, -1) q Himpunan Bilangan bulat A = { …, -4, -3, -2, -1, 0, 1, 2, 3, 4, … }

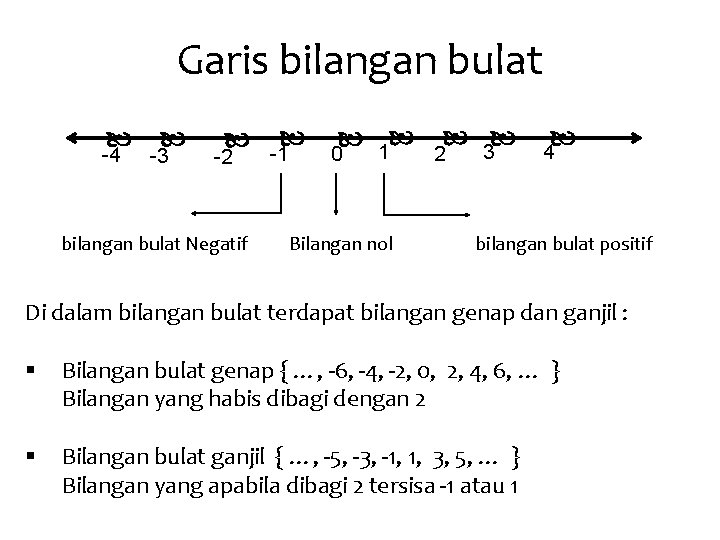
Garis bilangan bulat -4 -3 -2 bilangan bulat Negatif -1 1 0 Bilangan nol 2 3 4 bilangan bulat positif Di dalam bilangan bulat terdapat bilangan genap dan ganjil : § Bilangan bulat genap { …, -6, -4, -2, 0, 2, 4, 6, … } Bilangan yang habis dibagi dengan 2 § Bilangan bulat ganjil { …, -5, -3, -1, 1, 3, 5, … } Bilangan yang apabila dibagi 2 tersisa -1 atau 1

Operasi Hitung Bilangan Bulat • Penjumlahan ü Sifat Asosiatif ( a + b ) + c = a + ( b + c ) ü Sifat Komutatif a + b = b + a ü Unsur Identitas terhadap penjumlahan a + 0 = 0 + a ü Unsur invers terhadap penjumlahan a + (-a) = (-a) + a ü Bersifat tertutup a dan b ∈ bilangan bulat maka a + b = c ; c ∈ bilangan bulat

• Pengurangan ü Untuk sembarang bilangan bulat berlaku : a – b = a + (-b) a – (-b) = a + b ü Sifat Komutatif dan asosiatif tidak berlaku a – b ≠ b - a (a – b ) – c ≠ a – ( b – c ) ü Pengurangan bilangan nol mempunyai sifat : a – 0 = a dan 0 – a = -a ü Bersifat tertutup a dan b ∈ bilangan bulat maka a - b = c ; c ∈ bilangan bulat

• Perkalian ü a x b = ab , a x –b = -ab , -a x -b = ab ü Sifat Asosiatif (a x b) x c = a x (b x c) ü Sifat komutatif a x b = b x a ü Sifat distributif a x (b+c) = (a x b ) + (a x c) ü Unsur identitas untuk perkalian a x 0 = 0 atau a x 1 = 1 x a = a ü Bersifat tertutup a x b = c a, b, c ∈ bilangan bulat

• Pembagian ü Hasil bagi dua bilangan bulat positif adalah bilangan positif (+) : (+) = (+) ü Hasil bagi dua bilangan bulat negatif adalah bilangan positif (-) : (-) = (+) ü Hasil bagi dua bilangan bulat yang berbeda adalah bilangan negatif (+) : (-) = (-) atau (-) : (+) = (-) ü Hasil bagi bilangan bulat dengan 0 (nol) adalah tidak terdefinisi a : 0 (~) atau 0 : a 0 (nol) ü Tidak berlaku sifat komutatif dan asosiatif a : b ≠ b : a atau (a: b): c ≠ a : (b: c) ü Bersifat tidak tertutup

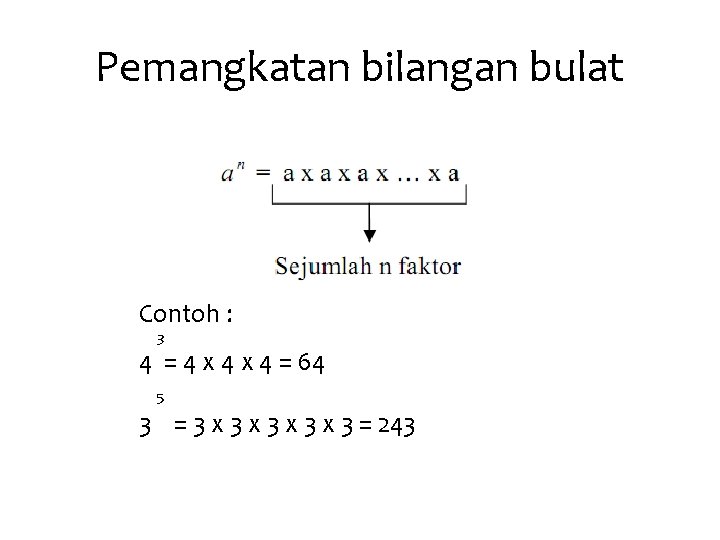
Pemangkatan bilangan bulat Contoh : 3 4 = 4 x 4 = 64 5 3 = 3 x 3 x 3 = 243

Akar pangkat dua • Akar kuadrat (akar pangkat dua)

Akar kubik (akar pangkat tiga)

Bilangan Riil

• Notasi dari himpunan bilangan riil adalah � • � dinyatakan sebagai garis lurus x є � dibaca x (sembarang bilangan) anggota dari � Jika x є � dinyatakan sebagai suatu titik di garis � x § Bilangan x terletak antara -a dan a dengan titik pusatnya 0 x x -a 0 a

Urutan Pada Garis Bilangan Riil Misalkan: x < y dibaca x berada di sebelah kiri y atau x lebih kecil dari y x > y dibaca x berada di sebelah kanan y atau y lebih kecil dari x • dibaca “ jika dan hanya jika” • x < y y-x positif

Sifat–sifat bilangan real • Sifat-sifat urutan : q. Trikotomi Jika x dan y adalah suatu bilangan, maka pasti berlaku salah satu dari x < y atau x > y atau x = y q. Ketransitifan Jika x < y dan y < z maka x < z q. Perkalian Misalkan z bilangan positif dan x < y maka xz < yz, sedangkan bila z bilangan negatif, maka xz > yz

q Penambahan x<y x+z <y+z q Relasi urutan dibaca “kurang dari atau sama dengan” dibaca “lebih dari atau sama dengan” x y y - x positif atau nol

Untuk setiap bilangan real a, b dan c berlaku sifat urutan berikut: • • • a a a < < > b a+c<b+c b a-c<b–c b, c > 0 ac < bc b, c < 0 ac > bc 0 • Jika a dan b bertanda sama maka

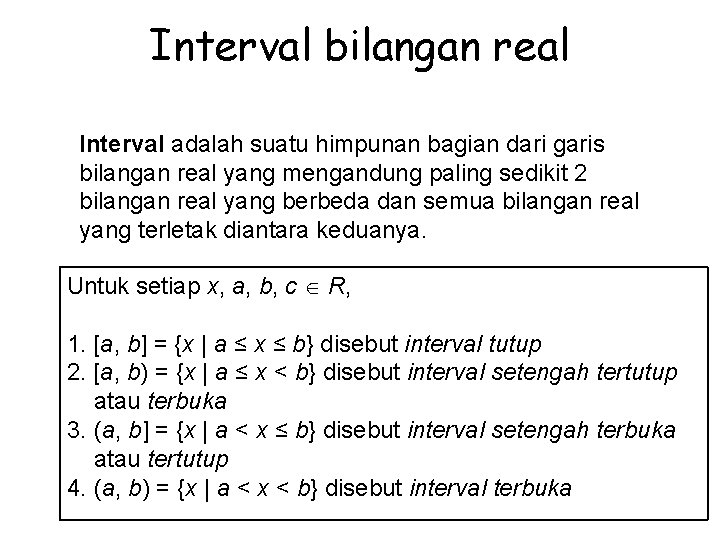
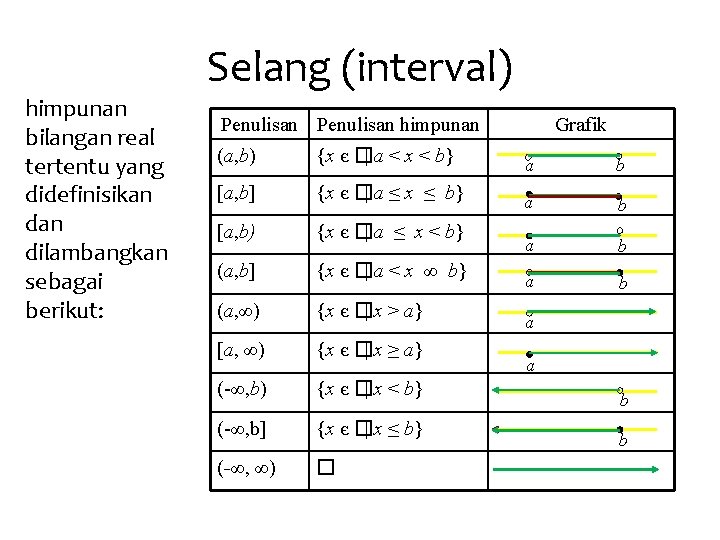
Interval bilangan real Interval adalah suatu himpunan bagian dari garis bilangan real yang mengandung paling sedikit 2 bilangan real yang berbeda dan semua bilangan real yang terletak diantara keduanya. Untuk setiap x, a, b, c R, 1. [a, b] = {x | a ≤ x ≤ b} disebut interval tutup 2. [a, b) = {x | a ≤ x < b} disebut interval setengah tertutup atau terbuka 3. (a, b] = {x | a < x ≤ b} disebut interval setengah terbuka atau tertutup 4. (a, b) = {x | a < x < b} disebut interval terbuka

Selang (interval) himpunan bilangan real tertentu yang didefinisikan dilambangkan sebagai berikut: Penulisan himpunan (a, b) {x є �| a < x < b} [a, b] {x є �| a ≤ x ≤ b} [a, b) {x є �| a ≤ x < b} (a, b] {x є �| a < x ∞ b} (a, ∞) {x є �| x > a} [a, ∞) {x є �| x ≥ a} (-∞, b) {x є �| x < b} (-∞, b] {x є �| x ≤ b} (-∞, ∞) � Grafik a b a b a a b b

Ketidaksamaan • Menyelesaikan ketidaksamaan dalam x berarti mencari interval atau interval-interval dari bilangan yang memenuhi ketidaksamaan tersebut. • Cara menyelesaikan ketidaksamaan : 1. tambahkan kedua sisi dengan bilangan yang sama 2. kalikan kedua sisi dengan bilangan positif 3. kalikan kedua sisi dengan bilangan negatif, tapi tanda ketidaksaman berubah Contoh: Selesaikan ketidaksamaan berikut dan gambarkanlah kumpulan solusinya pada garis bilangan real! a. 5 x – 3 ≤ 7 - 3 x b. c. (x – 1)2 ≤ 4

Nilai Mutlak • Definisi nilai mutlak : • Jadi |x|≥ 0 untuk setiap bilangan real x dan |x| = 0 jika dan hanya jika x = 0. • |x| dapat juga didefinisikan sebagai: • Secara Geometri: |x| menyatakan jarak dari x ke titik asal. |x – y| = jarak diantara x dan y

Sifat nilai mutlak • • |-a| = |a| |ab| = |a||b| • • • |a + b| ≤ |a| + |b| |x|2 = x 2 |x| < a jika dan hanya jika - a < x < a |x| > a jika dan hanya jika x > a atau x < -a |x| < |y| jika dan hanya jika x 2 < y 2

Contoh : • Selesaikan persamaan berikut: |2 x – 5|=9 • Tentukan solusi dari ketaksamaan berikut:

SOAL 3. Berapakah nilai a dan t yang memenuhi persamaan

INDUKSI MATEMATIKA • Induksi matematika adalah : Metode pembuktian untuk pernyataan perihal bilangan bulat. • Induksi matematik merupakan teknik pembuktian yang baku di dalam matematika.

1. Proposisi Perihal Bilangan Bulat. • Pernyataan perihal bilangan bulat mengkaitkan suatu masalah yang dihubungkan dengan bilangan bulat. • Untuk memberikan ilustrasi mengenai pernyataan yang dimaksud, diperlihatkan dengan memberikan contoh berikut :

Contoh 1 : Misalkan p(n) adalah pernyataan yang menyatakan : ”Jumlah bilangan bulat positif dari 1 sampai n adalah n (n+1) / 2. ” Buktikan bahwa p(n) benar! Jika dicoba dengan beberapa nilai n, memang timbul dugaan bahwa p(n) benar, misalnya untuk n = 5, p(5) adalah : “Jumlah bilangan bulat positif dari 1 sampai 5 adalah 5 (5+1)/2. Terlihat bahwa : 1 + 2 + 3 + 4 + 5 = 15 = 5 (6) / 2

Contoh 2 : Jika ingin menemukan rumus jumlah dari n buah bilangan ganjil positif yang pertama. Misalnya untuk n = 1, 2, 3, 4, 5, perhatikan jumlah n bilangan ganjil positif pertama , n=1 1=1 n=2 1+3=4 n=3 1+3+5=9 n = 4 1 + 3 + 5 + 7 = 16 n = 5 1 + 3 + 5 + 7 + 9 = 25 Dari nilai-nilai penjumlahan, bahwa jumlah n buah bilangan ganjil yang pertama adalah n 2

Contoh-contoh proposisi perihal bilangan bulat yang lainnya : 1. Setiap bilangan bulat positif n (n ≥ 2) dapat dinyatakan sebagai perkalian dari (satu atau lebih) bilangan prima. 2. Untuk semua n ≥ 1, n 3 + 2 n adalah kelipatan 3. 3. Untk membayar biaya pos sebesar n sen dolar (n ≥ 8) selalu dapat digunakan hanya perangko 3 sen dan 5 sen dolar. 4. Di dalam sebuah pesta, setiap tamu berjabat tangan dengan tamu lainnya hanya sekali. Jika ada n orang tamu maka jumlah jabat tangan yang terjadi adalah n(n – 1)/2. 5. Banyaknya himpunan bagian yang dapat dibentuk dari sebuah himpunan yang beranggotakan n elemen adalah 2.

2. Prinsip Induksi Sederhana • Misalkan p(n) adalah pernyataan perihal bilangan bulat positif dan kita ingin membuktikan bahwa p(n) benar untuk semua bilangan bulat positif n. Untuk membuktikan pernyataan ini, kita hanya perlu menunjukan bahwa : 1. p(1) benar, dan 2. jika p(n) benar, maka p(n+1) juga benar untuk semua bilangan bulat positif n 1.

Basis Induksi dan Langkah Induksi • Langkah 1 dinamakan Basis Induksi, sedangkan langkah 2 dinamakan Langkah Induksi. • Langkah induksi berisi asumsi (andaian) yang menyatakan bahwa p(n) benar. • Asumsi tersebut dinamakan hipotesis induksi. • Bila kedua langkah tsb benar, maka sudah dibuktikan bahwa p(n) benar untuk semua bilangan bulat positif n.

• Basis induksi digunakan untuk memperlihatkan bahwa pernyataan tersebut benar bila n diganti dengan 1, yang merupakan bilangan bulat positif terkecil. • Langkah induksi harus memperlihatkan bahwa p(n) p(n+1) benar untuk semua bilangan bulat positif.

Contoh 4. 1 : Tunjukkan bahwa untuk n 1, 1+2+3+…+n = n(n+1)/2 melalui induksi matematika (i) Basis induksi : p(1) benar, karena untuk n = 1 kita peroleh 1 = 1(1+1)/2 = 1(2)/2 1=1 (ii) Langkah induksi : kita harus memperlihatkan bahwa p(n+1) juga benar, 1+2+3+…+n+(n+1) = (n+1) [(n+1) +1] /2

1+2+3+…+n+(n+1) = (n+1) [(n+1) +1] /2 1+2+3+…+n+(n+1) = (1+2+3+…+n) + (n+1) = [n(n+1)/2] n(n+1)/2 + (n+1) = [(n 2 +n)/2] +n)/2 + [(2 n+2)/2] = (n 2 + 3 n + 2)/2 = (n+1)(n+2)/2 sama = (n+1) [(n+1)+1] /2 Karena langkah (i) dan (ii) telah dibuktikan benar, maka untuk semua bilangan bulat positif n, terbukti bahwa untuk semua n 1, 1+2+3+…+n = n(n+1)/2

Contoh 4. 3 : Tunjukkan bahwa untuk n 1, bahwa n 3 + 2 n adalah kelipatan 3 melalui induksi matematika (i) Basis induksi : p(1) benar, karena untuk n = 1, 13 + 2(1) = 3 adalah kelipatan 3 (ii) Langkah induksi : kita harus memperlihatkan bahwa p(n+1) juga benar, (n+1)3 + 2(n+1) adalah kelipatan 3

Hal ini dapat kita tunjukkan sbb: (n+1)3 + 2(n+1) = (n 3 + 3 n 2 + 3 n + 1) + (2 n + 2) = (n 3 + 2 n) + (3 n 2 + 3 n + 3) = (n 3 + 2 n) + 3(n 2 + n + 1) kelipatan 3

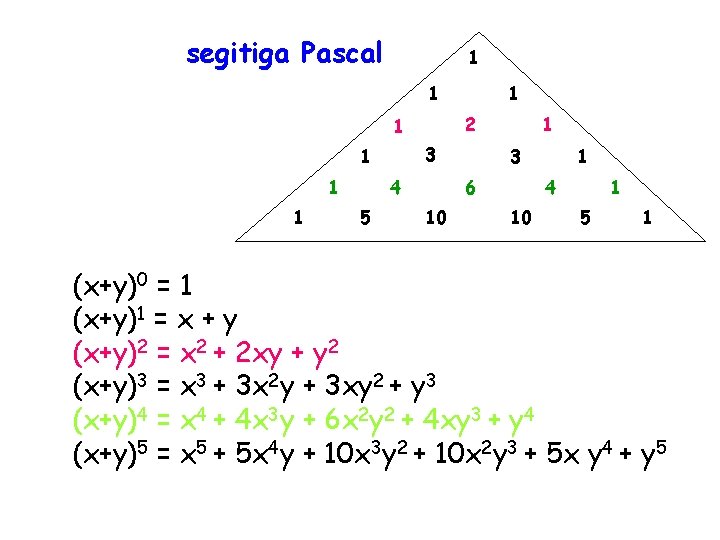
segitiga Pascal 1 1 2 1 3 1 4 1 1 5 1 1 3 6 10 1 4 10 1 5 1 (x+y)0 = 1 (x+y)1 = x + y (x+y)2 = x 2 + 2 xy + y 2 (x+y)3 = x 3 + 3 x 2 y + 3 xy 2 + y 3 (x+y)4 = x 4 + 4 x 3 y + 6 x 2 y 2 + 4 xy 3 + y 4 (x+y)5 = x 5 + 5 x 4 y + 10 x 3 y 2 + 10 x 2 y 3 + 5 x y 4 + y 5

3. Prinsip Induksi yang Dirampatkan. • Jika ingin membuktikan bahwa pernyataan p(n) benar untuk semua bilangan bulat n 0 , prinsip induksi sederhana dapat dirampatkan untuk menunjukkannya, dengan cara sebagai berikut : 1. p (n 0) benar, dan 2. jika p(n) benar maka p(n+1) juga benar untuk semua bilangan bulat n n 0

Contoh 4. 5 : Untuk semua bilangan bulat tidak negatif n, buktikan dengan induksi matematika bahwa 20+21+22+…+2 n = 2 n+1 -1 Misalkan p(n) adalah proposisi bahwa untuk semua bilangan bulat tidak negatif n, 20+21+22+…+2 n = 2 n+1 -1 (i) Basis induksi : p(0) benar, karena untuk n = 0 (bilangan bulat tidak negatif pertama), kita peroleh : 20 = 1 = 20+1 – 1 = 21 – 1 =2 – 1 =1

(ii) Langkah induksi : misalkan p(n) benar, yaitu proposisi Diasumsikan benar (hipotesis induksi). Kita harus menunjukkan bahwa p(n+1) juga benar, yaitu Hal ini kita tunjukkan sbb : sama