Lineris gpek 2014 mrc 20 Gpi tanulsi mdszerek

Lineáris gépek 2014. márc. 20.

Gépi tanulási módszerek eddig • Bayes döntéselmélet – Parméteres osztályozók – Nem paraméteres osztályozók • Fogalom tanulás – Döntési fák

2 Döntési felületek • Most a döntési függvények/felületek alakjára teszünk feltevéseket, abból indulunk ki • Nem optimális megoldások, de könnyen kezelhető eljárások • Lineáris osztályozókat (gépeket) adnak eredményül

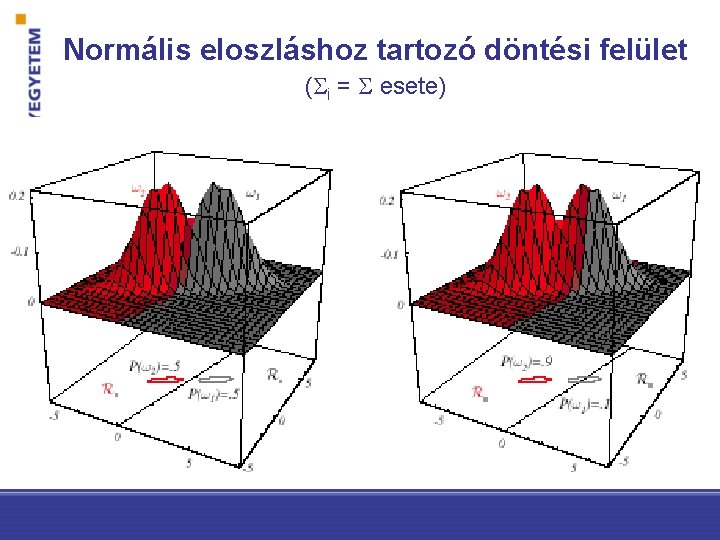
Normális eloszláshoz tartozó döntési felület ( i = esete)

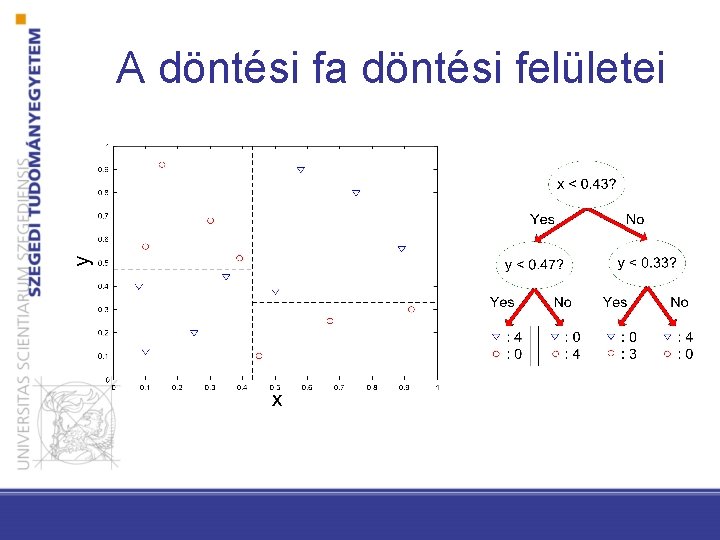
A döntési fa döntési felületei

Lineáris diszkriminancia függvények és döntési felületek 5 • két-kategóriás osztályozó: Válasszuk 1–et, ha g(x) > 0, 2–t, ha g(x) < 0 Válasszuk 1 –et, ha wtx > -w 0 és 2 –t különben Ha g(x) = 0 bármelyik osztályhoz rendelhetjük x –et • Lineáris diszkriminancia függvény: g(x) = wtx + w 0 w súlyvektor w 0 konstans (eltolás, bias)

6 – A g(x) = 0 definiálja azt a döntési felületet, amely elválasztja azokat a pontokat, amelyekhez 1 -et rendelünk, azoktól, amelyekhez 2 -t – Ha g(x) lineáris függvény, akkor a döntési felület egy hipersík Gyakran fontos, hogy az x távolságát a hipersíktól meghatározzuk

7

8 H távolsága az origótól: A döntési felület irányát a w normál vektora határozza meg, míg a helyét a konstans

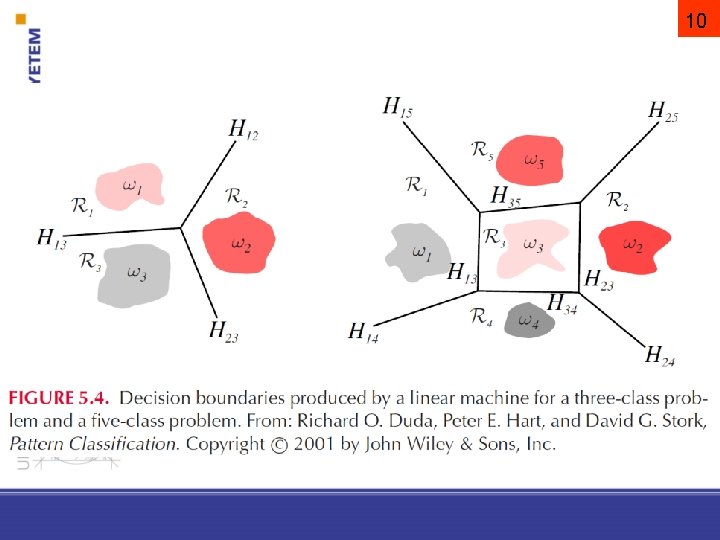
Ha több, mint 2 osztályunk van c darab lineáris diszkriminancia függvényt definiálunk és az x mintát a i osztályhoz rendeljük, ha gi(x) > gj(x) j i; ha a legnagyobb értéknél egyenlőség van, határozatlan 9

10

Ha több, mint 2 osztályunk van Ri döntési tartomány: az a térrész ahol gi(x) értéke a legnagyobb A folytonos Ri és Rj döntési tartományokat a Hij hipersík egy része választja el a hipersík definíciója: gi(x) = gj(x) Û (wi – wj)tx + (wi 0 – wj 0) = 0 wi – wj merőleges (normál vektor) Hij -re és

Konvexitás Könnyű megmutatni, hogy a lineáris géppel definiált döntési tartományok konvexek. Ez rontja az osztályozó flexibilitását és pontosságát… Az osztályokat elválasztó döntési felületek nem feltétlenül lineárisak, a döntési felület bonyolultsága gyakran magasabb rendű (nem lineáris) felületek használatát indokolja 12

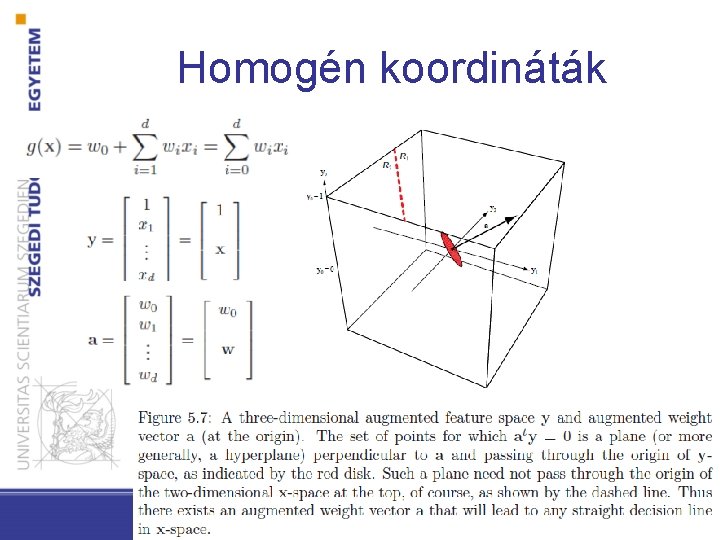
Homogén koordináták

14 Lineáris gépek tanulása

Lineáris gépek tanulása • Határozzuk meg a döntési felület paraméteres alakját • Adott tanuló példák segítségével adjuk meg a „legjobb” felületet • Ezt általában valamilyen kritériumfüggvény minimalizálásával tesszük meg – Pl. tanulási hiba 15

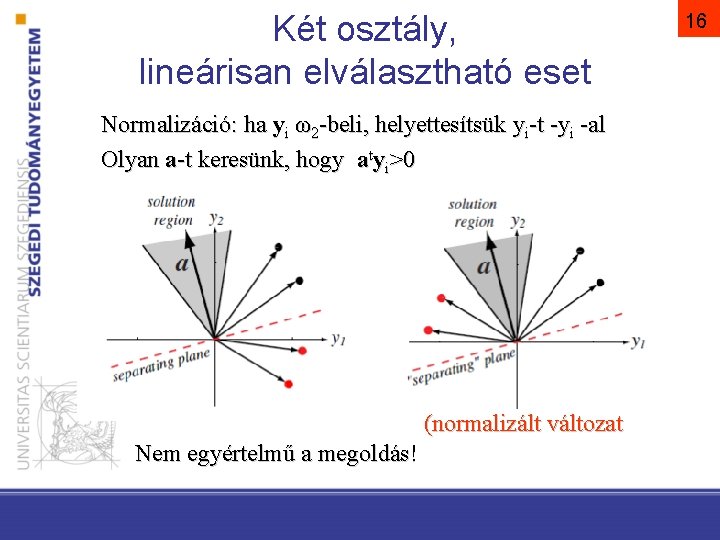
Két osztály, lineárisan elválasztható eset Normalizáció: ha yi ω2 -beli, helyettesítsük yi-t -yi -al Olyan a-t keresünk, hogy atyi>0 (normalizált változat Nem egyértelmű a megoldás! 16

Iteratív optimalizálás • Definiáljunk egy J(a) kritériumfüggvényt, amely minimális, ha a megoldásvektor. • Minimalizáljuk J(a) –t iteratív módon a(k+1) a(k) Keresési irány Tanulási arány 17

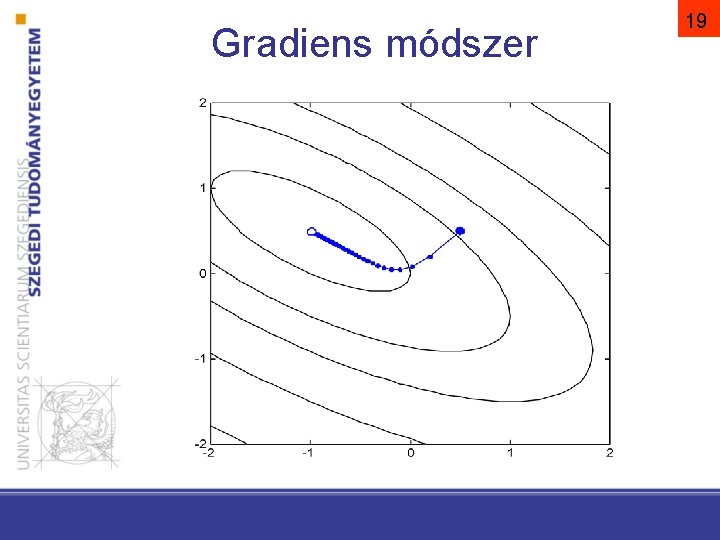
Gradiens módszer Tanulási arány, k-től függ, pl. „hűtési stratégia” 18

Gradiens módszer 19

Tanulási arány? 20

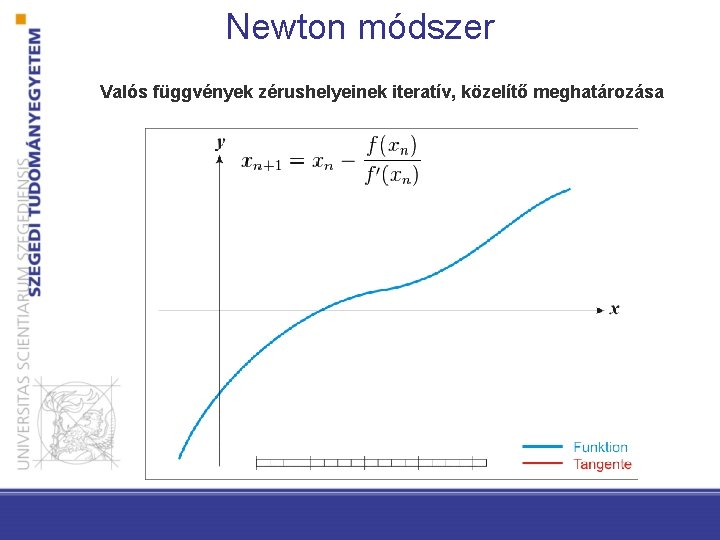
Newton módszer Valós függvények zérushelyeinek iteratív, közelítő meghatározása

22 Newton módszer • Hogyan válasszuk a h(k) tanulási arányt? Taylor sorba fejtés Hess mátrix

Gradiens és Newton összehasonlítása 23

Perceptron szabály

Perceptron szabály Kritérium Függvény: Y(a): a által rosszul osztályzott minták halmaza. Ha Y(a) üres, Jp(a)=0; különben, Jp(a)>0

Perceptron szabály 26 – A Jp(a) gradiense: – A perceptron szabály gradiens módszerbeli alkalmazásával kapható:

Perceptron szabály 27 Az összes rosszul osztályzott minta Online osztályozó: tanító példák hozzáadásával frissül a modell

28 Perceptron szabály η(k)=1 egyesével vegyük a példákat Perceptron konvergencia tétel: Ha a mintánk lineárisan szeparálható, akkor a fenti algoritmus súlyvektora véges számú lépésben megoldást ad.

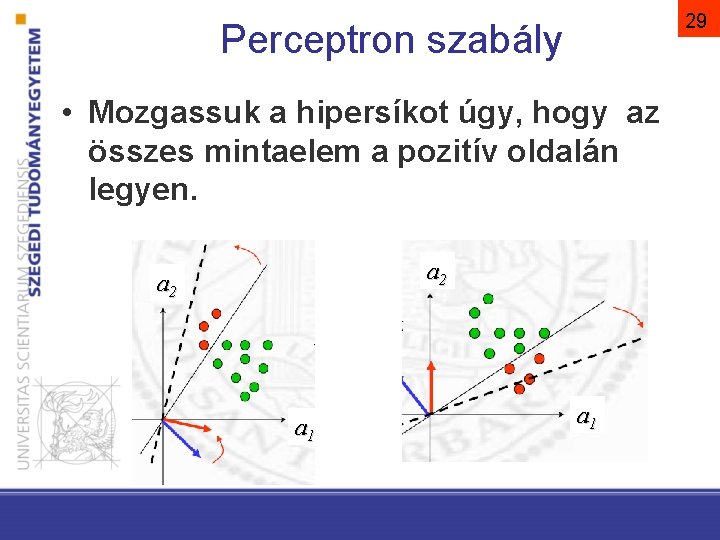
29 Perceptron szabály • Mozgassuk a hipersíkot úgy, hogy az összes mintaelem a pozitív oldalán legyen. a 2 a 1

30 Nem-szeparálható eset – Alkalmazhatunk más kritériumfüggvényt: a kritériumfüggvény minden mintaelemet figyelembe vesz – „jósági” mérték lehet például a döntési felülettől mért előjeles távolság

SVM

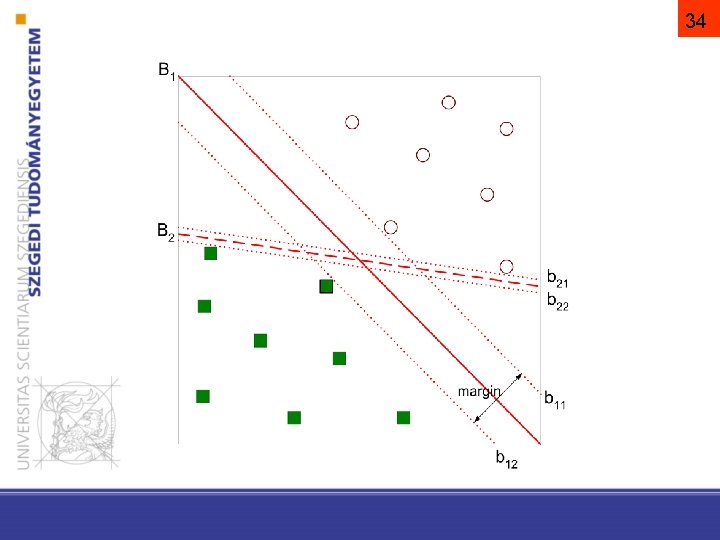
32 Melyik megoldás jobb?

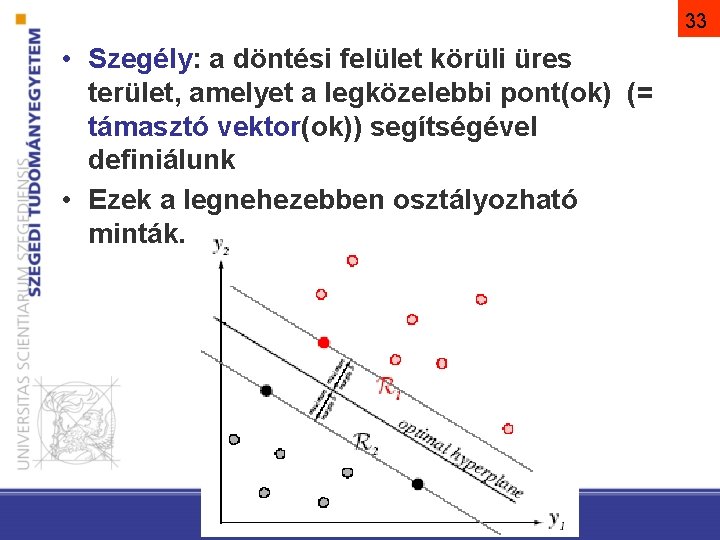
33 • Szegély: a döntési felület körüli üres terület, amelyet a legközelebbi pont(ok) (= támasztó vektor(ok)) segítségével definiálunk • Ezek a legnehezebben osztályozható minták.

34

SVM (support vector machine) 35 • támasztó vektorok módszere, szupport vektor gép • A kritérium függvény legyen az osztályok közötti szegély maximalizálása! • Ez jó általánosítást szokott biztosítani • A tanítás ekvivalens egy lineáris feltételekkel adott kvadratikus programozási feladattal

SVM lineárisan elválasztható eset

Lineáris SVM: az elválasztható eset • Lineáris diszkriminancia válasszuk ω1 ha g(x) > 0 egyébként ω2 • Osztálycímkék • Normalizált változat: 37

Lineáris SVM: az elválasztható eset • Tfh a margó mérete b • Az xk pontnak az elválasztó hipersíktól való távolságára teljesülnie kell: • Az egyértelműség biztosítására: b||w||=1 • Így az előző feltétel: 38

Lineáris SVM: az elválasztható eset A szegély maximalizálása: 39

Lineáris SVM: az elválasztható eset 40 minimalizálás w-ben, max λ-ban Könnyebb a duális probléma megoldása: z kz j=-1 ha különböző előjelűek a k. és j. tanítópéldák Alkalmazzunk Lagrange optimalizálást:

Lineáris SVM: az elválasztható eset 41 A megoldás a következő alakú: A döntési felület a tanító példák „súlyozott átlaga” Megmutatható, hogy ha xk nem támasztóvektor, akkor λk=0. csak a támasztóvektorok járulnak a megoldáshoz!!

SVM lineárisan nem elválasztható eset

• A ψk hibaváltozó bevezetésével hibás osztályozást is megenged („puha szegély”): Szabályozhatjuk a téves osztályozások számát vs. margó méretét Lineáris SVM: a nemelválasztható eset 43 ψk=0 ha g(xk)=zk (azaz b margón kívül van), egyébként a margótól mért távolság

Lineáris SVM: a nemelválasztható eset 45

SVM nem lineáris eset

Általánosított lineáris diszkriminancia függvények 47 • Kvadratikus döntési függvények: • Általános lineáris döntési függvények: ahol az yi: Rd → R tetszőleges függvények x-ben nem lineáris, de yi-ben g(y) igen (az y-térben g(x) hipersík)

Példa

Kvadratikus felület A használt kvadratikus függvények a következő kvadratikus felülettel írhatók le: g(x) = x. TAx + x. Tb +c ahol az A = (aij) mátrix, a b = (b 1, b 2, …, bd)T vektor, c konstans 51

Kvadratikus felület 52 Ha A pozitív definit (x. TAx>0 minden nemzéró x-re), akkor a döntési függvény hiperellipszoid, amelynek tengelyei az A sajátvektorainak irányába mutatnak (ha A = In (egységmátrix), akkor a döntési függvény az ndimenziós hipergömb) Ha A negatív definit (x. TAx<0 minden nemzéró x-re), akkor a döntési függvény hiperboloid Lényeg: ebben az esetben az A mátrix határozza meg a döntési függvény alakját és jellemzőit

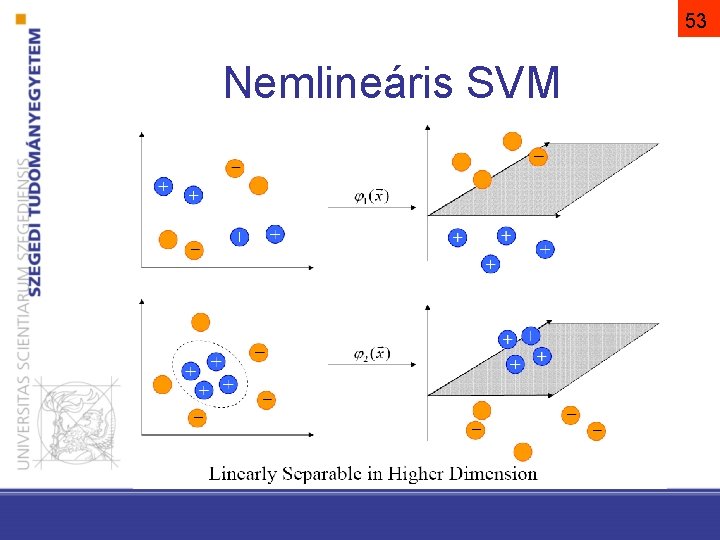
53 Nemlineáris SVM

54 Nemlineáris SVM Φ legyen (jóval) magasabb dimenzószámú térbe leképezés: Bármilyen adathalmaz, megfelelően nagy dimenzióba történő alkalmas leképezéssel lineárisan elválasztható lesz az új térben!

55 Nemlineáris SVM lineáris gép: lineáris SVM-nél: Lineáris SVM a leképzett térben:

56 A magfüggvény trükkje A belső szorzatokat egy magfüggvény (kernel) segítségével számoljuk! A kernel használatának előnyei – Nem kell ismerni Φ()-t !! – A diszkriminancia a következő alakú:

57 Példa: polinomiális kernel K(x, y)=(x y) p d=256 (eredeti dimenziószám) p=4 h=183 181 376 (új tér dimenziószáma) a kernel ismert (és gyorsan számítható) a leképezés nem…

Egy kernel több leképezésnek is megfelel Ezek is megfelelőek: 58

59 Megfelelő magfüggvények • K-nek eleget kell tenni a „Mercer” feltételeknek • A projektált tér nem egyértelmű és nem ad támpontot magfgv tervezéshez…

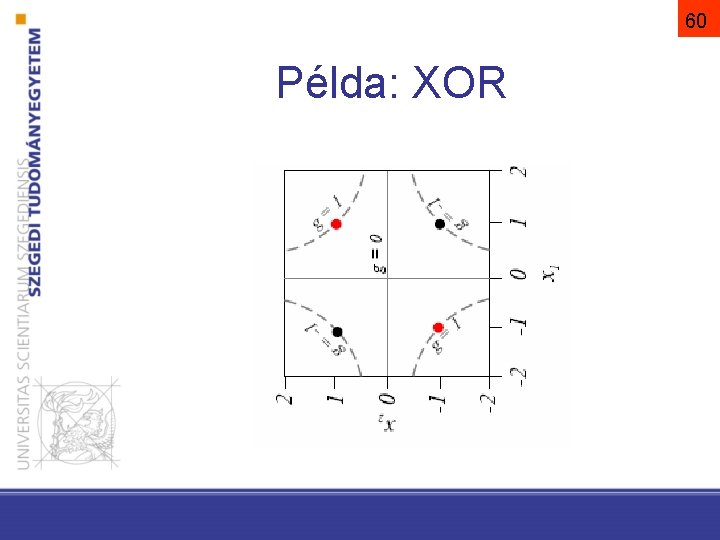
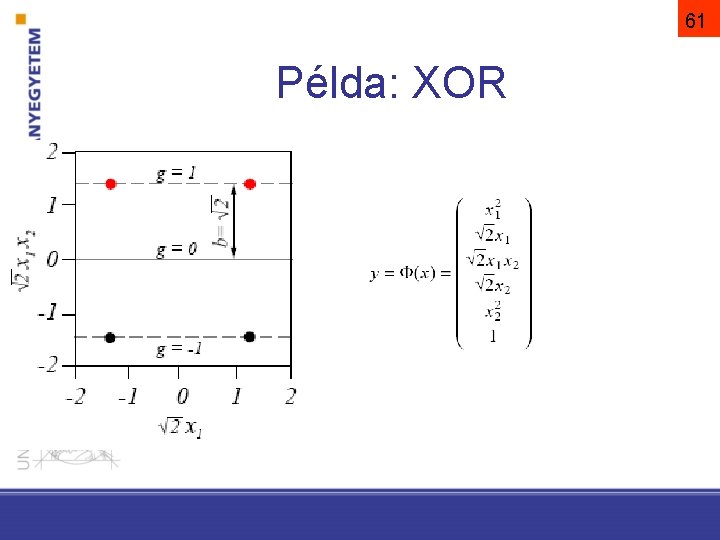
60 Példa: XOR

61 Példa: XOR

62 Példa: XOR

63 Példa: XOR

64 Megjegyzések az SVM-hez • Globális optimalizálás, nem lokális (pontos optimum, nem közelítés). • Az SVM hatékonysáka a magfüggvény és paramétereinek választásától függ • Egy adott problémához a legjobb magfüggvény választása „művészet”

65 Megjegyzések az SVM-hez • A komplexitása a támasztó vektorok számától, és nem a transzformált tér dimenziójától függ • A gyakorlatban kis mintánál is jó általánosítási tulajdonságok • Többosztályos SVM: – one-vs-all (legnagyobb g()) – one-vs-one (legtöbb győzelem) – direkt optimalizáció

Összefoglalás • • Lineáris gépek Gradiens és Newton módszer Perceptron SVM – Szeparálható eset – Nem szeparálható eset – Nem lineáris eset (magfüggvény)