Optimalizlsi mdszerek 1 A lineris vektortr Kiegszt gpsz

Optimalizálási módszerek 1. A lineáris vektortér Kiegészítő gépész levelezők 2003/2004 -es tanév II. félév Optimalizálási módszerek Kiegészítő gépész levelező Miskolci Egyetem 1

Vektorok, a lineáris vektortér - 1 Definíció: (vektor) Vektoron rendezett szám n-est fogunk érteni. (Valós számokkal dolgozunk. ) A szám n-esben szereplő számokat koordinátáknak nevezzük. A vektor rövid jelölésére vastagított kisbetűket használunk. Pl: x=(x 1, …, xn). Definíció: (két vektor összeadása) Legyen x=(x 1, …, xn), y=(y 1, …, yn) két n elemű vektor. A két vektor összege egy z=(z 1, …, zn) harmadik vektor az alábbi szerint: x+y=(x 1+y 1, …, xn+yn)=(z 1, …, zn)=z Az összeadás tulajdonságai: - kommutativitás: x+y=y+x - asszociativitás: (x+y)+z=x+(y+z) - invertálhatóság: bármely x, y esetén az x+z=y egyenletnek létezik z megoldása. Definíció: (Nullvektor, zérusvektor) Olyan 0 -val jelzett vektor, amelyre bármely x vektor esetén teljesül az x+0=x összefüggés. 0=(0, …, 0) Optimalizálási módszerek Kiegészítő gépész levelező Miskolci Egyetem 2

Vektorok, a lineáris vektortér - 2 Definíció: (Vektor szorzása számmal) Legyen x=(x 1, …, xn) egy vektor és valós szám. Az x vektor -szorosán azt a z= x vektort értjük, amely képzési szabálya: z= x = ( x 1, …, xn) A vektor szorzása számmal művelet tulajdonságai - vektor disztributivitás: (x+y)= x+ y - skalár disztributivitás: ( + )x= x+ x - skalár asszociativitás: ( )x= ( x) - egységelemmel szorzás: 1 x=x Definíció: (Lineáris vektortér) Vektorok összessége, melyben a fenti két művelet bevezetésre került. Optimalizálási módszerek Kiegészítő gépész levelező Miskolci Egyetem 3

Skaláris szorzat Definíció: (Két vektor skaláris szorzata) Legyen x=(x 1, …, xn), y=(y 1, …, yn) két n elemű vektor. Két vektor skaláris szorzatán azt az xy-nal jelzett valós számot értjük, amelynek képzési szabálya: xy= x 1 y 1+…+xnyn A skaláris szorzat tulajdonságai: - kommutativitás: xy=yx - disztributivitás: (x+y)z=xz+yz - skalár asszociativitás: ( x)y= (xy) - pozitivitás: xx 0 egyenlőséggel akkor és csak akkor, ha x=0. Optimalizálási módszerek Kiegészítő gépész levelező Miskolci Egyetem 4

A lineáris kombináció Definíció: (Vektorok lineáris kombinációja) Ha a b vektor az a 1, a 2, …, an vektorok és a 1, …, n valós számok segítségével a b= 1 a 1+…+ nan alakban áll elő, akkor azt mondjuk, hogy b az a 1, a 2, …, an vektorok lineáris kombinációja 1, …, n együtthatókkal. Definíció: (Generáló rendszer) Egy vektorrendszer részhalmazát a vektorrendszer generáló rendszerének nevezzük, ha a rendszer minden eleme előáll a részhalmaz lineáris kombinációjaként. Definíció: (Független rendszer) Egy vektorrendszert lineárisan függetlennek nevezünk, ha egyetlen eleme sem állítható elő a többiek lineáris kombinációjaként. Egyetlen vektorból álló rendszert lineárisan függetlennek nevezünk, ha az nem a zérusvektor. Definíció: (Bázisrendszer) Egy vektorrendszer bázisrendszere (röviden bázisa) az olyan részrendszer, amely lineárisan független és generáló rendszer is egyidejűleg. A bázisrendszer által a rendszer minden eleme egyértelműen fejezhető ki. Az így kapott lineáris kombinációban szereplő együtthatókat a vektor adott bázisbeli koordinátáinak nevezzük. Optimalizálási módszerek Kiegészítő gépész levelező Miskolci Egyetem 5

A Steinitz tétel Tétel: (Steinitz tétel, független és generáló forma) Egy vektorrendszer bármely lineárisan független részrendszerében a vektorok száma nem lehet több, mint bármely generáló részrendszerében a vektorok száma. Tétel: (Steinitz tétel, bázisforma) Egy vektorrendszer bármely bázisa azonos számú vektorból áll. Definíció: Mesterséges bázis e 1=(1, 0, 0, …, 0, 0) e 2=(0, 1, 0, …, 0, 0) e 3=(0, 0, 1, …, 0, 0) … en-1=(0, 0, 0, …, 1, 0) en =(0, 0, 0, …, 0, 1) Optimalizálási módszerek Kiegészítő gépész levelező Miskolci Egyetem 6

Vektorrendszer rangja Definíció: (Vektorrendszer rangja (mátrixrang, sorrang, oszlop-rang)) A vektorrendszer egy (bármely) bázisában lévő vektorok számát a vektorrendszer rangjának nevezzük. Jele: rang(a 1, a 2, …, an) Definíció: (Lineáris altér és dimenziója (rangja)) Lineáris altérnek nevezzük egy vektorrendszer tagjai által generált összes lehetséges lineáris kombinációinak összességét. Ezen altér rangja megegyezik a vektorrendszer rangjával. Optimalizálási módszerek Kiegészítő gépész levelező Miskolci Egyetem 7

Bázistábla és tulajdonságai Adott bázis esetén egy vektorrendszer tagjait koordinátáikkal egy táblázatba (úgynevezett bázistáblába) foglalhatjuk. A táblázat fejlécében felsoroljuk a rendszer tagjait, a tábla balszélén pedig felsoroljuk a bázisbeli elemeket. Maga a tábla a vektorok koordinátáit tartalmazza az adott bázisban a tábla balszélének megfelelő kiosztásban. Optimalizálási módszerek a 1 … an b 1 t 11 … t 1 n … … bm tm 1 … tmn Kiegészítő gépész levelező Miskolci Egyetem 8

Pivotálás Tétel: Pivotálás=bázisvektorcsere hatása a bázistáblára Ha a bázistáblában valamely vektornak (legyen az s indexű) valamely koordinátája (legyen az r indexű) nem zérus, akkor a bázisban az r indexű vektort kicserélhetjük a kiszemelt s indexű vektorra. A bázistábla ezáltal a következő módon változik meg: Optimalizálási módszerek Kiegészítő gépész levelező Miskolci Egyetem 9

Ortogonalitási tétel Tétel: Ortogonalitási tétel Ugyanazon vektorrendszer két tetszőleges bázistáblája esetén fennáll a ti’tk”=0 összefüggés. Itt ti’ az első tábla i-dik sora, tk” pedig a második tábla k-dik oszlopa kiegészítve olyan vektorrá, amelyben annyi koordináta van, mint a vektorrendszer tagjainak a száma, miközben a kiegészítés zérusokkal történik, kivéve a k-dik koordinátát, ahol a kiegészítő elem – 1. A k-dik oszlopban a koordináták olyan indexelés szerint olvasandók, mint az első tábla i-dik sorában. Optimalizálási módszerek Kiegészítő gépész levelező Miskolci Egyetem 10

Kompozíciós tétel Tétel: Kompozíciós tétel Legyen a bázistábla kezdetben olyan, hogy a bázisban az egységvektorok (mesterséges bázis) találhatók. a 1 … an e 1 … em e 1 a 11 … a 1 n 1 … 0 … … … … em a 1 m … amn 0 … 1 Ekkor tetszőleges számú pivotálás után T=YA. Sematikusan a 1 … an e 1 … em Optimalizálási módszerek b 1 t 11 … t 1 n y 11 … y 1 m … … … … bm t 1 m … tmn y 1 m … ymm Kiegészítő gépész levelező Miskolci Egyetem 11

Mátrix rangja és inverze Mátrix rangjának meghatározása Mátrix rangja meghatározható azáltal, hogy oszlopait vektoroknak tekintve hány vektort tudunk a bázisba bevonni az egységvektorok helyére. A rang a bevont oszlopok száma. Mátrix inverzének meghatározása Négyzetes mátrix esetén ha a bázisba az összes oszlopot sikerült bevinni, akkor a bázistáblában az Y mátrix helyén keletkezik az eredeti inverze. A bázisban lévő vektorok indexeit a kiolvasásnál figyelembe kell venni. Optimalizálási módszerek Kiegészítő gépész levelező Miskolci Egyetem 12

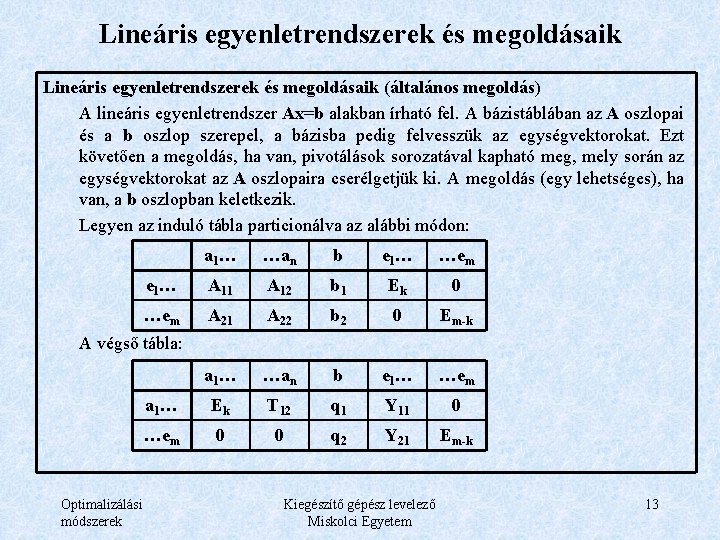
Lineáris egyenletrendszerek és megoldásaik (általános megoldás) A lineáris egyenletrendszer Ax=b alakban írható fel. A bázistáblában az A oszlopai és a b oszlop szerepel, a bázisba pedig felvesszük az egységvektorokat. Ezt követően a megoldás, ha van, pivotálások sorozatával kapható meg, mely során az egységvektorokat az A oszlopaira cserélgetjük ki. A megoldás (egy lehetséges), ha van, a b oszlopban keletkezik. Legyen az induló tábla particionálva az alábbi módon: a 1… …an b e 1 … A 11 A 12 b 1 …em A 21 A 22 b 2 a 1… …an b a 1… Ek T 12 q 1 Y 11 …em 0 0 q 2 Y 21 e 1 … …em Ek 0 0 Em-k e 1 … …em A végső tábla: Optimalizálási módszerek 0 Em-k Kiegészítő gépész levelező Miskolci Egyetem 13

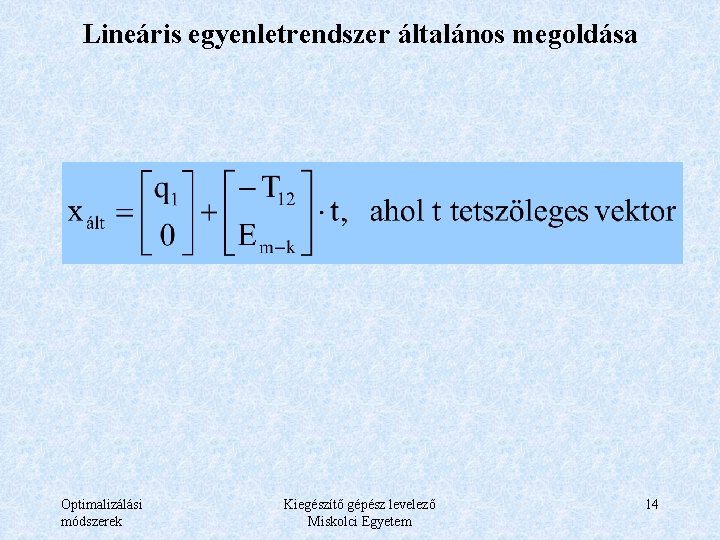
Lineáris egyenletrendszer általános megoldása Optimalizálási módszerek Kiegészítő gépész levelező Miskolci Egyetem 14

Bázismegoldás Definíció: A lineáris egyenletrendszer bázismegoldása Bázismegoldásnak nevezzük egy lineáris egyenletrendszer megoldását, ha a nembázisbeli koordináták zérusok, a bázisbeliek pedig nemzérusok. Degenerált bázismegoldásról beszélünk, ha a bázisbeliek között is előfordul zérus. Definíció: A lineáris egyenletrendszer nemnegatív bázismegoldásai Ha a bázismegoldásban a bázisbeli koordináták pozitívak akkor nemnegatív bázismegoldásról beszélünk. Optimalizálási módszerek Kiegészítő gépész levelező Miskolci Egyetem 15