Limits introduction Alex Karassev The concept of a

Limits (introduction) Alex Karassev

The concept of a limit What happens to x 2 when x approaches 2? ¢ Look at table of values: ¢ x x 2 1. 999 3. 61 3. 9601 3. 996001 |x 2 - 4| 0. 39 0. 0399 0. 003999 2. 1 2. 001 4. 41 4. 0401 4. 004001 0. 41 0. 0401 0. 004001

Direct substitution Thus we see that x 2 approaches 4, i. e. 22, as x approaches 2 ¢ So we can just substitute 2 in the function x 2 ¢ Is it always the case? ¢

Example: direct substitution is impossible Look at (x 3 -1)/(x-1) as x approaches 1 ¢ We cannot sub. x=1, however, we can substitute the values of x near 1 ¢ x 0. 999 (x 3 -1)/(x-1) 2. 71 2. 9701 2. 997001 x 1. 1 1. 001 (x 3 -1)/(x-1) 3. 31 3. 0301 3. 003001 0. 9999 2. 99970001 1. 0001 3. 00030001 Guess: (x 3 - 1) / (x - 1) approaches 3 as x approaches 1

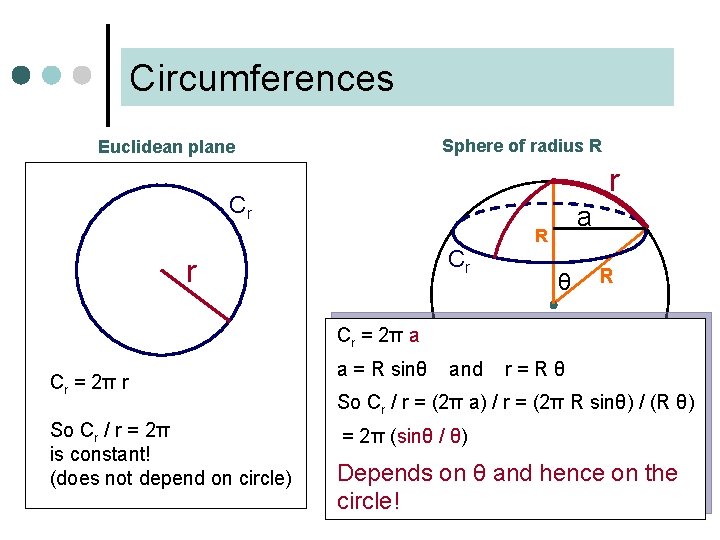
Measuring the earth… How to decide whether a planet is flat or "round"? ¢ Look at circles of the same radius on a sphere and on the plane and compare their circumferences ¢

Circumferences Sphere of radius R Euclidean plane r Cr Cr r a R θ R Cr = 2π a Cr = 2π r So Cr / r = 2π is constant! (does not depend on circle) a = R sinθ and r=Rθ So Cr / r = (2π a) / r = (2π R sinθ) / (R θ) = 2π (sinθ / θ) Depends on θ and hence on the circle!

What if θ is very small? r When θ is small the piece of sphere enclosed by our circle is "almost flat", so we should expect that Cr Cr / r is very close to 2π θ However, Cr / r = 2π (sinθ / θ) Therefore, when θ is close to 0, sinθ / θ is close to 1 ! θ is close to 0 Guess: sinθ / θ approaches 1 as θ approaches 0 Equivalently: sinθ ≈ θ when θ is near 0

Example: what is sin 1° ? sinθ ≈ θ when θ is near 0 ¢ 1° = π / 180 radians, so θ = π / 180 ¢ We have: sin 1° = sin (π / 180) ≈ π / 180 ≈ 3. 14 / 180 = 0. 0174444… ¢ Calculator gives: sin 1° ≈ 0. 017452406 ¢

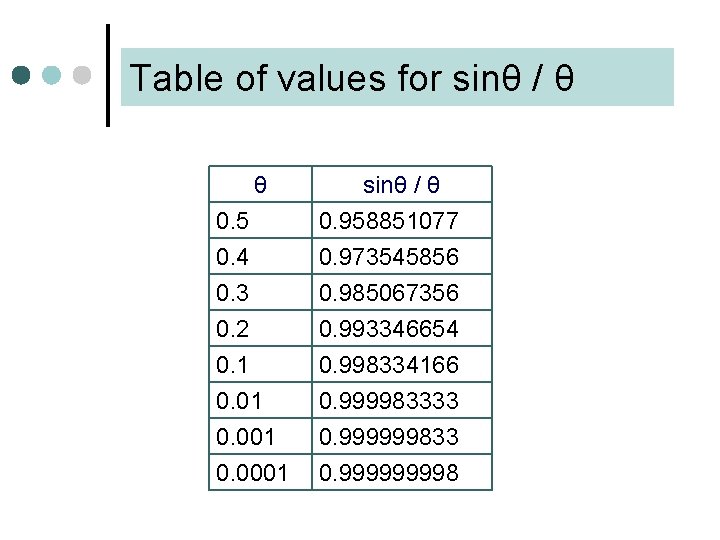
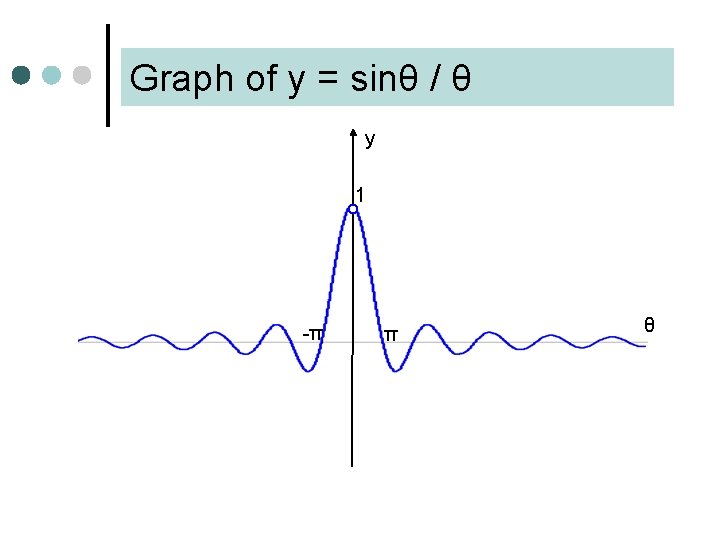
Table of values for sinθ / θ θ 0. 5 0. 4 0. 3 sinθ / θ 0. 958851077 0. 973545856 0. 985067356 0. 2 0. 1 0. 001 0. 0001 0. 993346654 0. 998334166 0. 999983333 0. 999999833 0. 99998

Graph of y = sinθ / θ y 1 -π π θ

Danger of guessing ¢ What happens to when x approaches 0? x f(x) 0. 010099828 0. 0011 0. 0002 0. 00001 0. 00011 What is our guess?

Danger of guessing ¢ More values… x f(x) 0. 0011 0. 0002 0. 00001 0. 00011 0. 000001 0. 000101 0. 0000001 0. 0001001 0. 00000001 0. 0001 What is our guess now?

Solution ¢ As x approaches 0: ¢ sinx approaches sin 0 = 0 ¢ cosx approaches cos 0 = 1 ¢ So sinx + cosx / 10000 approaches 0 + 1 / 10000 = 0. 0001 ¢

Informal definition ¢ We write if we can make the values of f(x) as close to L as we like by taking x to be sufficiently close to a but not equal to a ¢ Note: the value of function f at a, i. e. f(a), does not affect the limit!

Examples y 4 y=f(x) x 2 When we compute limit as x approaches 2, x is not equal to 2

Does limit always exist? y y=h(x) 1 0 x ¢ If x approaches 0 from the left then h(x) is constantly 0 ¢ If x approaches 0 from the right then h(x) is constantly 1 ¢ Thus when x is close to 0 h(x) can be arbitrarily close (in fact, even equal to) 0 or 1 and we cannot choose either of this two numbers for the value of the limit of h(x) as x approaches 0 ¢ So does not exists (D. N. E. )

One-sided limits Limit of f(x) as x approaches a from the left ¢ Limit of f(x) as x approaches a from the right ¢

From the left ¢ We write if we can make the values of f(x) as close to L as we like by taking x to be sufficiently close to a and less than a f(a) y y = f(x) L x x a

From the right ¢ We write if we can make the values of f(x) as close to L as we like by taking x to be sufficiently close to a and more than a f(a) y y = f(x) L a x x

Theorem

Infinite limits Let f(x) = 1/x 2 ¢ If x is close 0 then 1/x 2 is a very large positive number ¢ Therefore the finite limit of 1/x 2 as x approaches 0 does not exist ¢ However, we may say that 1/x 2 approaches positive infinity as x approaches 0 ¢ y M 0 x

Infinite limits We write if we can make the values of f(x) bigger than any number M by taking x to be sufficiently close to a and not equal to a (note: think of M as of large positive number) ¢ We write if we can make the values of f(x) smaller than any number M by taking x to be sufficiently close to a and not equal to a (note: think of M as of large negative number) ¢

Infinite limits: one-sided limits y x 0

Vertical asymptote ¢ Definition we say that a line x=a is a vertical asymptote for the function f if at leas one of the following is true:

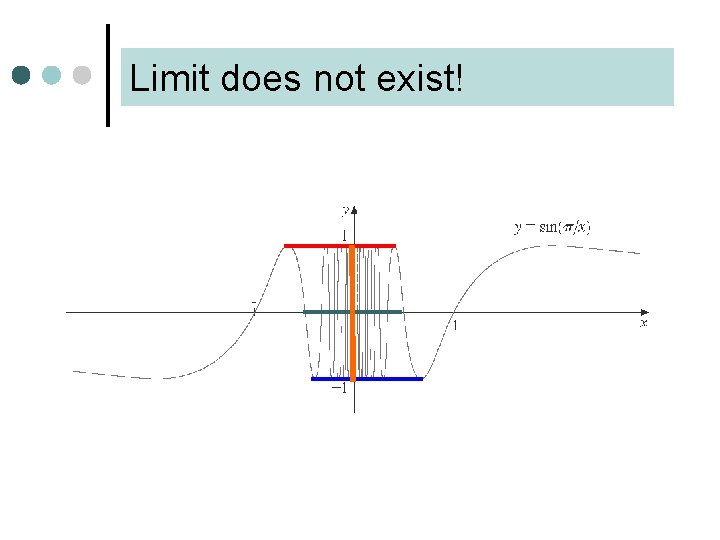
Example What happens when x approaches 0? x 1/2 1/3 1/4 sin(π/x) sin(π/1/2)=sin(2 π)=0 0 0 1/n sin(π/1/n)=sin(πn)=0

However… x 2/5 2/9 2/13 2/17 2/(4 n+1) sin(π/x) sin(π/2/5)=sin(5/2)π= sin(π/2 + 2 π) = sin(π/2) = 1 1 1

Limit does not exist!