Continuity Alex Karassev Definition l A function f

Definition l A function f is continuous at a number a if l Thus,

Some remarks l Definition of continuity requires three things: q q q l f(a)

Continuous functions and limits l Theorem Suppose that f is continuous at b and

Properties of continuous functions l Suppose f and g are both continuous at a

Which functions are continuous? l Theorem q Polynomials, rational functions, root functions, power functions,

Example l Determine, where is the following function continuous:

Solution l l l According to the previous theorem, we need to find domain

Definitions l l A solution of equation is also called a root of equation

Intermediate Value Theorem (IVT) l l f is continuous on [a, b] N is

Equivalent statement of IVT l l l l f is continuous on [a, b]

Equivalent statement of IVT l l f is continuous on [a, b] f(a) and

Continuity is important! y l l Let f(x) = 1/x Let a = -1

Important remarks l l IVT can be used to prove existence of a root

Example 1 l l Prove that equation x = 3 – x 5 has

Steps to prove that x = 3 – x 5 has a solution l

Example 2 l Find approximate solution of the equation x = 3 – x

Idea: method of bisections l Use the IVT to find an interval [a, b]

f(x) = x 5 + x – 3 = 0 We already know that

Exercise l Prove that the equation sin x = 1 – x 2 has

Slides: 28

Download presentation

Continuity Alex Karassev

Definition l A function f is continuous at a number a if l Thus, we can use direct substitution to compute the limit of function that is continuous at a

Some remarks l Definition of continuity requires three things: q q q l f(a) is defined (i. e. a is in the domain of f) exists Limit is equal to the value of the function The graph of a continuous functions does not have any "gaps" or "jumps"

Continuous functions and limits l Theorem Suppose that f is continuous at b and Then l Example

Properties of continuous functions l Suppose f and g are both continuous at a Then f + g, f – g, fg are continuous at a q If, in addition, g(a) ≠ 0 then f/g is also continuous at a q l Suppose that g is continuous at a and f is continuous at g(a). Then f(g(x)) is continuous at a.

Which functions are continuous? l Theorem q Polynomials, rational functions, root functions, power functions, trigonometric functions, exponential functions, logarithmic functions are continuous on their domains q All functions that can be obtained from the functions listed above using addition, subtraction, multiplication, division, and composition, are also continuous on their domains

Example l Determine, where is the following function continuous:

Solution l l l According to the previous theorem, we need to find domain of f Conditions on x: x – 1 ≥ 0 and 2 – x >0 Therefore x ≥ 1 and 2 > x So 1 ≤ x < 2 Thus f is continuous on [1, 2)

Intermediate Value Theorem

River and Road

Definitions l l A solution of equation is also called a root of equation A number c such that f(c)=0 is called a root of function f

Intermediate Value Theorem (IVT) l l f is continuous on [a, b] N is a number between f(a) and f(b) q l i. e f(a) ≤ N ≤ f(b) or f(b) ≤ N ≤ f(a) then there exists at least one c in [a, b] s. t. f(c) = N y y = f(x) f(b) N f(a) a cb x

Equivalent statement of IVT l l l l f is continuous on [a, b] N is a number between f(a) and f(b), i. e f(a) ≤ N ≤ f(b) or f(b) ≤ N ≤ f(a) then f(a) – N ≤ N – N ≤ f(b) – N or f(b) – N ≤ N – N ≤ f(a) – N so f(a) – N ≤ 0 ≤ f(b) – N or f(b) – N ≤ 0 ≤ f(a) – N Instead of f(x) we can consider g(x) = f(x) – N so g(a) ≤ 0 ≤ g(b) or g(b) ≤ 0 ≤ g(a) There exists at least one c in [a, b] such that g(c) = 0

Equivalent statement of IVT l l f is continuous on [a, b] f(a) and f(b) have opposite signs q l i. e f(a) ≤ 0 ≤ f(b) or f(b) ≤ 0 ≤ f(a) then there exists at least one c in [a, b] s. t. f(c) = 0 y y = f(x) f(b) a N=0 c x b f(a)

Continuity is important! y l l Let f(x) = 1/x Let a = -1 and b = 1 f(-1) = -1, f(1) = 1 However, there is no c such that f(c) = 1/c =0 1 x -1 0 1 -1

Important remarks l l IVT can be used to prove existence of a root of equation It cannot be used to find exact value of the root!

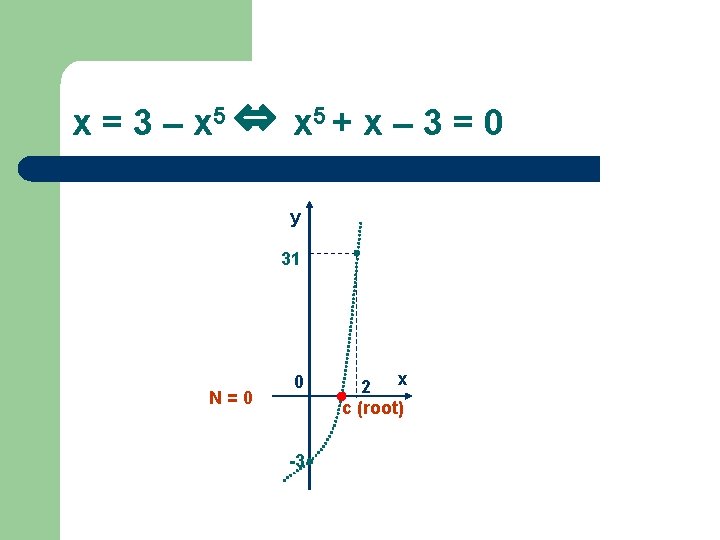
Example 1 l l Prove that equation x = 3 – x 5 has a solution (root) Remarks Do not try to solve the equation! (it is impossible to find exact solution) q Use IVT to prove that solution exists q

Steps to prove that x = 3 – x 5 has a solution l Write equation in the form f(x) = 0 q l Check that the condition of IVT is satisfied, i. e. that f(x) is continuous q l l x 5 + x – 3 = 0 so f(x) = x 5 + x – 3 is a polynomial, so it is continuous on (-∞, ∞) Find a and b such that f(a) and f(b) are of opposite signs, i. e. show that f(x) changes sign (hint: try some integers or some numbers at which it is easy to compute f) q Try a=0: f(0) = 05 + 0 – 3 = -3 < 0 q Now we need to find b such that f(b) >0 q Try b=1: f(1) = 15 + 1 – 3 = -1 < 0 does not work q Try b=2: f(2) = 25 + 2 – 3 =31 >0 works! Use IVT to show that root exists in [a, b] q So a = 0, b = 2, f(0) <0, f(2) >0 and therefore there exists c in [0, 2] such that f(c)=0, which means that the equation has a solution

x = 3 – x 5 ⇔ x 5 + x – 3 = 0 y 31 N=0 0 -3 2 x c (root)

Example 2 l Find approximate solution of the equation x = 3 – x 5

Idea: method of bisections l Use the IVT to find an interval [a, b] that contains a root l Find the midpoint of an interval that contains root: midpoint = m = (a+b)/2 l Compute the value of the function in the midpoint l If f(a) and f (m) are of opposite signs, switch to [a, m] (since it contains root by the IVT), otherwise switch to [m, b] l Repeat the procedure until the length of interval is sufficiently small

f(x) = x 5 + x – 3 = 0 We already know that [0, 2] contains root f(x)≈ -3 0 x <0 -1 Midpoint = (0+2)/2 = 1 >0 31 2

f(x) = x 5 + x – 3 = 0 f(x)≈ -3 0 x -1 6. 1 31 1 1. 5 2 Midpoint = (1+2)/2 = 1. 5

f(x) = x 5 + x – 3 = 0 f(x)≈ -3 0 x -1 1. 3 6. 1 31 1 1. 25 1. 5 2 Midpoint = (1+1. 5)/2 = 1. 25

f(x) = x 5 + x – 3 = 0 f(x)≈ -3 -1 -. 07 1. 3 1 1. 125 0 x 1. 25 6. 1 31 1. 5 2 Midpoint = (1 + 1. 25)/2 = 1. 125 l By the IVT, interval [1. 125, 1. 25] contains root l Length of the interval: 1. 25 – 1. 125 = 0. 125 = 2 / 16 = = the length of the original interval / 24 l 24 appears since we divided 4 times l Both 1. 25 and 1. 125 are within 0. 125 from the root! l Since f(1. 125) ≈ -. 07, choose c ≈ 1. 125 l Computer gives c ≈ 1. 13299617282. . .

Exercise l Prove that the equation sin x = 1 – x 2 has at least two solutions Hint: Write the equation in the form f(x) = 0 and find three numbers x 1, x 2, x 3, such that f(x 1) and f(x 2) have opposite signs AND f(x 2) and f(x 3) have opposite signs. Then by the IVT the interval [ x 1, x 2 ] contains a root AND the interval [ x 2, x 3 ] contains a root.