Numerical Solution of Quantum Wave Equations II NonRelativistic































- Slides: 36

Numerical Solution of Quantum Wave Equations: II Non-Relativistic (Schroedinger) 1. Computing quantum ground states 2. Fluid dynamic formulation of QM 3. Implicit methods for QM Sauro Succi

Time indep SE (TISE) The time-indep Schroendiger is: Hilbert expansion in orthonormal eigenfunctions: Delivers the Linear Eigenvalue Problem” 2

Special cases Hermite Polynomials (cartesian geometry, harmonic oscillator) Laguerre polynomials (radial symmetry) Spherical harmonics (radial + 2 angular coordinates} 3

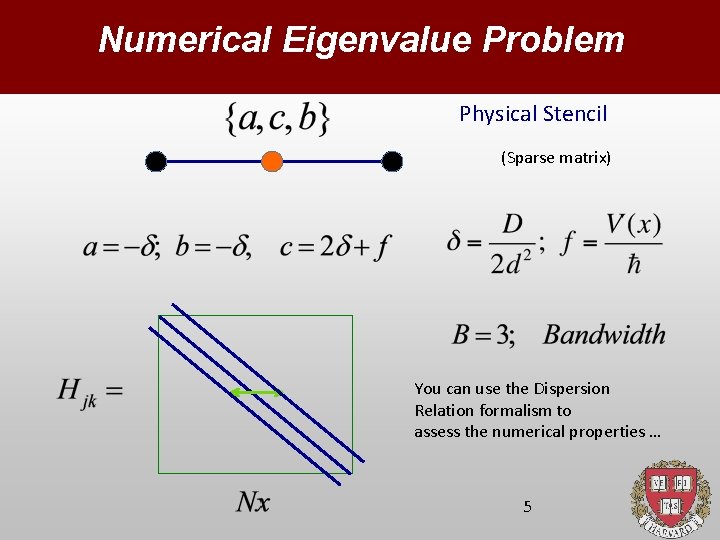
Numerical Eigenvalue Problem Physical Stencil (Sparse matrix) You can use the Dispersion Relation formalism to assess the numerical properties … 4

Numerical Eigenvalue Problem Physical Stencil (Sparse matrix) You can use the Dispersion Relation formalism to assess the numerical properties … 5

Eigenvalues by power method Trial function Such that: Note that the eigenfunctions need not be known at this stage, We just assume they exist with a sequential spectrum 6

Eigenvalues by power method Krylov sequence: 7

Eigenvalues by power method Krylov sequence: 8

Eigenvalues by power method Since all epsilons<1, raising to power p is a prowerful suppressor. In teh end we are left with Extract E_0: 9

Major Extensions Non-linear SE: optics, Bose-Einstein condensates (Gross-Pitaevski) Random potentials: Anderson Localization Theory of random matrices N-body Schroedinger: a world of its own (Computational Chemistry) 10

The imaginary-time SCE Make time imaginary through a Wick rotation: The imaginary time Schroendiger is: Known face: Diffusion-Reaction (linear, inhomogeneous) What for? If you let evolve long enough all excited modes die out except the ground state 11

Imag-Time Projection Assuming a discrete, ordered , real-valued spectrum: The imaginary-time evolution “projects out” all excited states. In the end, we are left with the ground state only. Very nice, but ……………. ? 12

Compute excited states Same Hilbert expansion, without the term n=0 Repeat the evolution up to t>1/omega 1: using the initial condition: Works well only if the eigenvalues are well separated! 13

Quantum Mechanics in Fluid form (Quantum tornado…) 14

Eikonal (Madelung) Eikonal form: Let: Simple algebra yields: The SCE becomes: Real part: Imag part: 15

Quantum Mech in Fluid form Imag part: Multiply by R: Continuity Equation! The quantum-fluid correspondence is: 16

Quantum Mech in Fluid form Real part: Take the gradient * 2 D Define the quantum potential: This is an inviscid fluid with zero pressure (remember Burgers? ) subject to the classical potential V(x) plus the self-consistent quantum potential Q(x)! 17

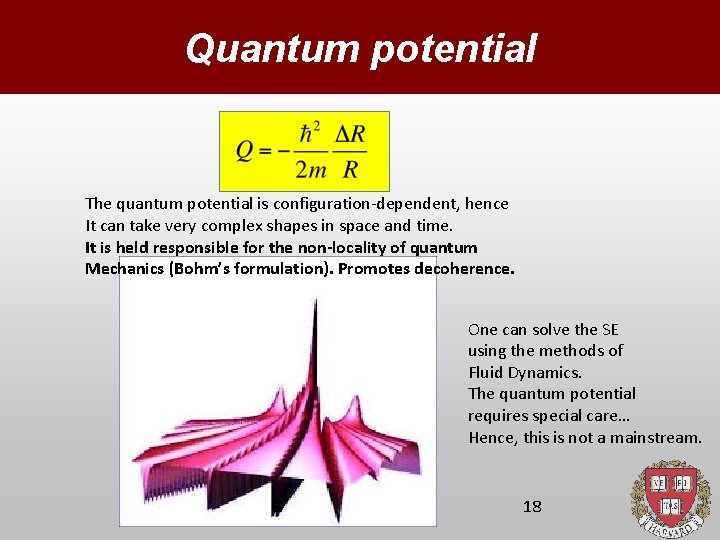
Quantum potential The quantum potential is configuration-dependent, hence It can take very complex shapes in space and time. It is held responsible for the non-locality of quantum Mechanics (Bohm’s formulation). Promotes decoherence. One can solve the SE using the methods of Fluid Dynamics. The quantum potential requires special care… Hence, this is not a mainstream. 18

Specific Quantum potential 19

Numerical Fluid Methods Since the quantum wavefunction is a pressureless inviscid fluid, one can solve it using the computational fluid methods. Not easy because: i) there is no dissipation, ii) the quantum potential is weird (non-linear and non-local) The common trend is to use Lagrangian Particle Methods 20

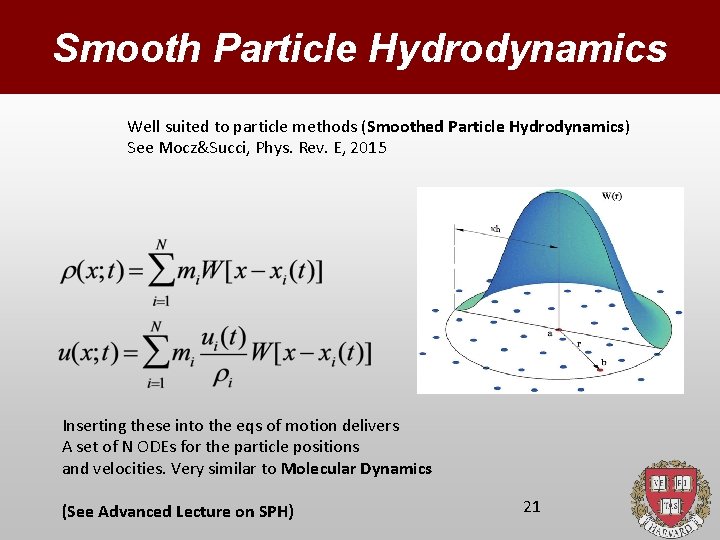
Smooth Particle Hydrodynamics Well suited to particle methods (Smoothed Particle Hydrodynamics) See Mocz&Succi, Phys. Rev. E, 2015 Inserting these into the eqs of motion delivers A set of N ODEs for the particle positions and velocities. Very similar to Molecular Dynamics (See Advanced Lecture on SPH) 21

Implicit Methods 22

Transfer Operator: back to ADR Let us discuss Implicit methods from a general perspective. It is then convenient to go back to classical systems. Back to ADR in Liouville form (no imaginary unit): Formal solution: Q: how do we compute the propagator in practice? 23

Time Marching: Quadrature Exact! Must approximate On the lattice x_j=j*d: Perform the integral numerically 24

Explicit vs Implicit Using a (generalized) trapezoidal rule: Instead of taking high order derivatives at present time t (predictors), Jump ahead into the future! Fully Explicit Semi-Implicit (Crank-Nicolson) Fully Implicit 25

Theta=0: Euler, no good First order in time: Unconditionally unstable! 26

Theta=1/2: Crank-Nicolson, good Implicit methods: Crank-Nicolson: Break Causality but gain Unitarity. Doable because the quantum dynamics is reversible, no causal arrow. This is a MATRIX problem A*x=b: The scheme is unitary: For any timestep! Hence: q. e. d. 27

Theta=1, no good … Hence The scheme is stable, but non-unitary and only first order accurate. Since it still involves a matrix problem, no point versus Crank-Nicolson 28

General Theory of Propagators Pade’ approximants of the exponential Where P_N, P_M are polynomials of degree N and M, respectively Explicit: M=0, Implicit: M>0 Euler: N=1, M=0 Crank-Nicolson: N=M=1 Fully Implicit: N=0, M=1 Very Important for Path-Integral formulation of quantum mechanics! Unitarity requires N=M: Past and Future are symmetric 29

Geometrical summary Continuum: Discrete: The unitary operator “rotates” the wavefunction by an angle h. L (orange). Euler (black) amplifies the “vector” , Fully Implicit compresses it, Crank-Nicolson (green) rotates by a slighly different angle, 2*tan(h. L/2), 30 but still rotates it without changing the amplitude = 1

Crank-Nicolson: Solving the matrix problem 31

1 D: tridiagonal matrices Physical Stencil (Sparse matrix) You can use the Dispersion Relation formalism to assess the numerical properties … 32

1 d Matrix Problem Physical Stencil This can be solved by any Linear Algebra Solver In d=1 this can be done algebraically, but in d=2, 3 requires O(N^2) operations, unless iterative methods are used. An extra lecture on this is probably healthy… 33

Summary The Schroedinger equation can be viewed as diffusion-reaction equation in imaginary time and also like a peculiar fluid equation subject to the quantum potential. Numerics: Explicit: Euler is unconditionally unstable Explicit: Sync Visscher is fine Implicit: Crank-Nicolson is unitary and allows large time-steps, but it may become expensive unless specialized linear algebra is used Matter of taste somehow… Fluid methods must handle the quantum potential with great care Eigenvalue solvers constantly in progress (Time-Independent SCE) 34

Assignments 1. Compute the ground state of the harmonic oscillator using imag-time SCE 2. Same for a square-well 3. Comment on the shape of the quantum potential for both 2 and 3 35

End of lecture 36
 Origin of quantum mechanics
Origin of quantum mechanics Quantum physics vs mechanics
Quantum physics vs mechanics Numerical methods for partial differential equations eth
Numerical methods for partial differential equations eth Cauchy equation
Cauchy equation Quantum wave equation
Quantum wave equation Quantum physics wave function
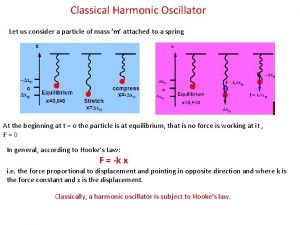
Quantum physics wave function Classical harmonic oscillator
Classical harmonic oscillator Wave function of quantum harmonic oscillator
Wave function of quantum harmonic oscillator Quantum physics wave function
Quantum physics wave function Review of quantum mechanics
Review of quantum mechanics Electrodynamics
Electrodynamics Light is an electromagnetic wave true or false
Light is an electromagnetic wave true or false Long waves and short waves
Long waves and short waves Difference between full wave and half wave rectifier
Difference between full wave and half wave rectifier Transverse and longitudnal waves
Transverse and longitudnal waves Half full wave rectifier
Half full wave rectifier Full wave rectification circuit
Full wave rectification circuit P and s wave chart
P and s wave chart Rectified sine wave fourier series
Rectified sine wave fourier series Wave wave repeating
Wave wave repeating Wave wave repeating
Wave wave repeating When does a wave posses a quarter wave symmetry?
When does a wave posses a quarter wave symmetry? Venn diagram of mechanical and electromagnetic waves
Venn diagram of mechanical and electromagnetic waves Examples of a mechanical wave
Examples of a mechanical wave Wavelength formula triangle
Wavelength formula triangle Wave equation solution
Wave equation solution Wave velocity formula
Wave velocity formula Derivation of time independent schrodinger equation
Derivation of time independent schrodinger equation Vapour pressure
Vapour pressure Adam moulton method
Adam moulton method No solution system of equations
No solution system of equations Natural solution
Natural solution Consistent system of equations
Consistent system of equations Bisection method solved examples
Bisection method solved examples Polar to rectangular equation
Polar to rectangular equation Translating chemical equations
Translating chemical equations Numerical expression and equation
Numerical expression and equation