Classical Harmonic Oscillator Let us consider a particle

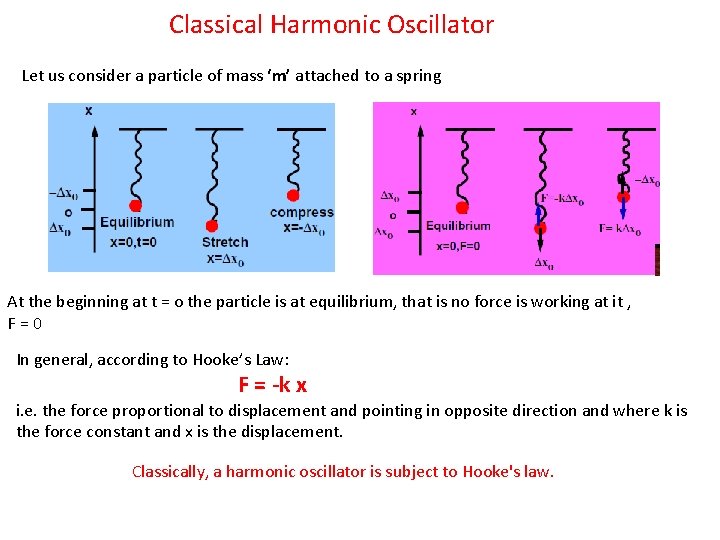
Classical Harmonic Oscillator Let us consider a particle of mass ‘m’ attached to a spring At the beginning at t = o the particle is at equilibrium, that is no force is working at it , F=0 In general, according to Hooke’s Law: F = -k x i. e. the force proportional to displacement and pointing in opposite direction and where k is the force constant and x is the displacement. Classically, a harmonic oscillator is subject to Hooke's law.

Newton's second law says Therefore, F = ma The solution to this differential equation is of the form: where the angular frequency of oscillation is ‘ω’ in radians per second Also, ω = 2πʋ, where ‘ʋ’ is frequency of oscillation

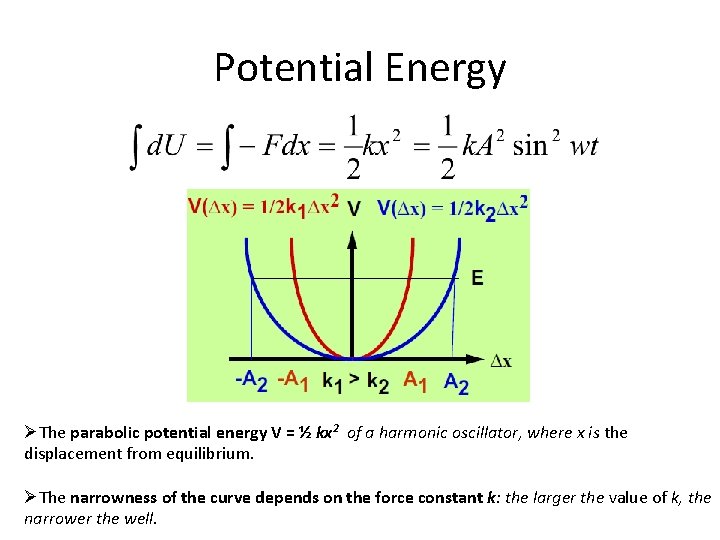
Potential Energy ØThe parabolic potential energy V = ½ kx 2 of a harmonic oscillator, where x is the displacement from equilibrium. ØThe narrowness of the curve depends on the force constant k: the larger the value of k, the narrower the well.

Kinetic energy

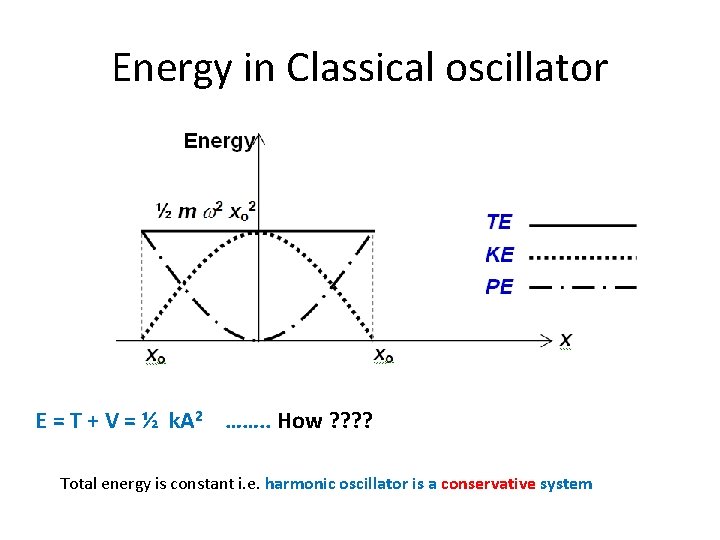
Energy in Classical oscillator E = T + V = ½ k. A 2 ……. . How ? ? Total energy is constant i. e. harmonic oscillator is a conservative system

Quantum Harmonic Oscillator In classical physics, the Hamiltonian for a harmonic oscillator is given by: where μ denotes the reduced mass: The quantum mechanical harmonic oscillator is obtained by replacing the classical position and momentum by the corresponding quantum mechanical operators.

Solution of Schrӧdinger Equation for Quantum Harmonic Oscillator

It is only possible if

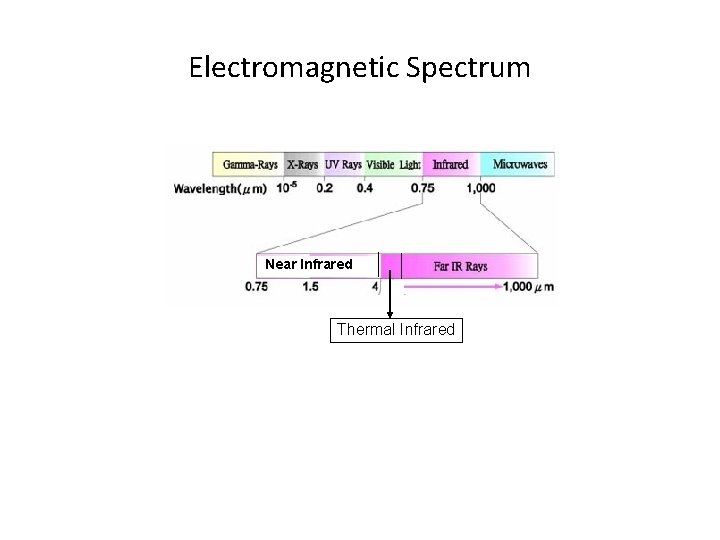
Electromagnetic Spectrum Near Infrared Thermal Infrared

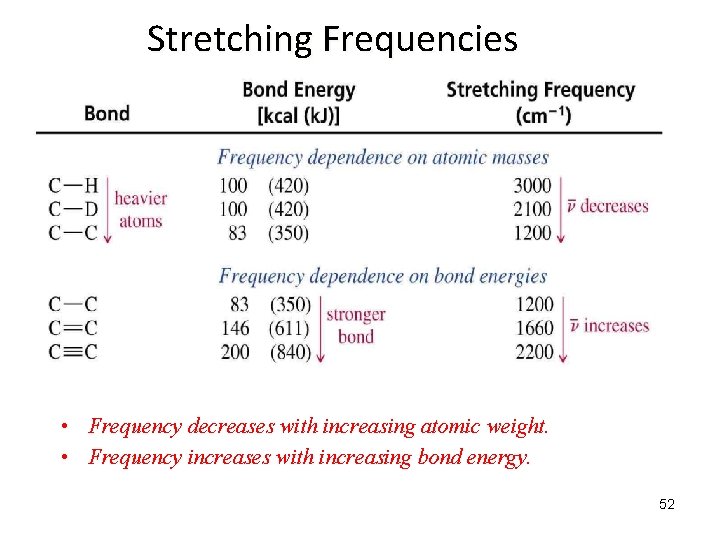
IR Stretching Frequencies of two bonded atoms: What Does the Frequency, , Depend On? = frequency k = spring strength (bond stiffness) = reduced mass (~ mass of largest atom) is directly proportional to the strength of the bonding between the two atoms ( k) is inversely proportional to the reduced mass of the two atoms (v 1/ ) 51

Stretching Frequencies • Frequency decreases with increasing atomic weight. • Frequency increases with increasing bond energy. 52

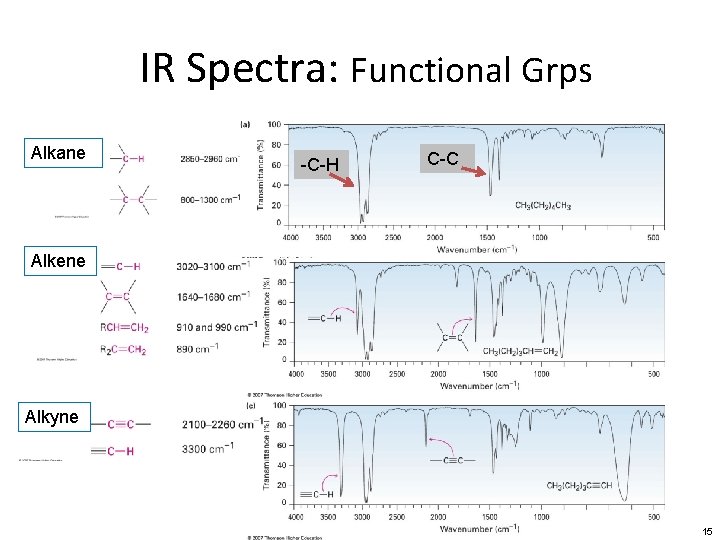
IR spectroscopy is an important tool in structural determination of unknown compound

IR Spectra: Functional Grps Alkane -C-H C-C Alkene Alkyne 15

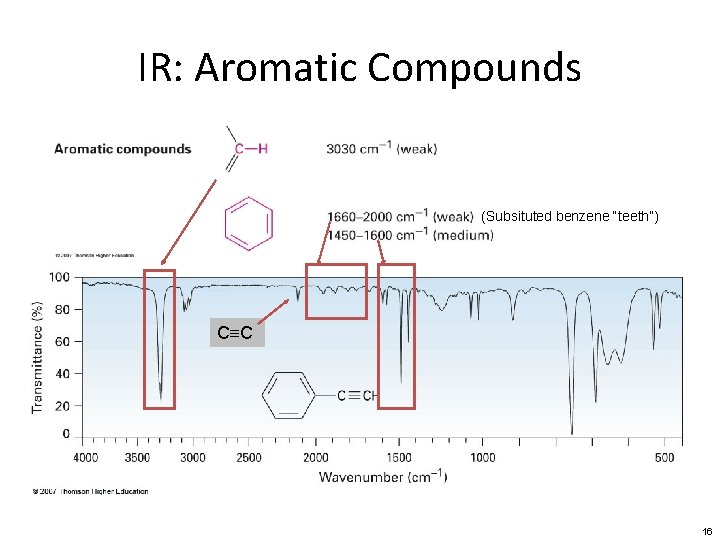
IR: Aromatic Compounds (Subsituted benzene “teeth”) C≡C 16

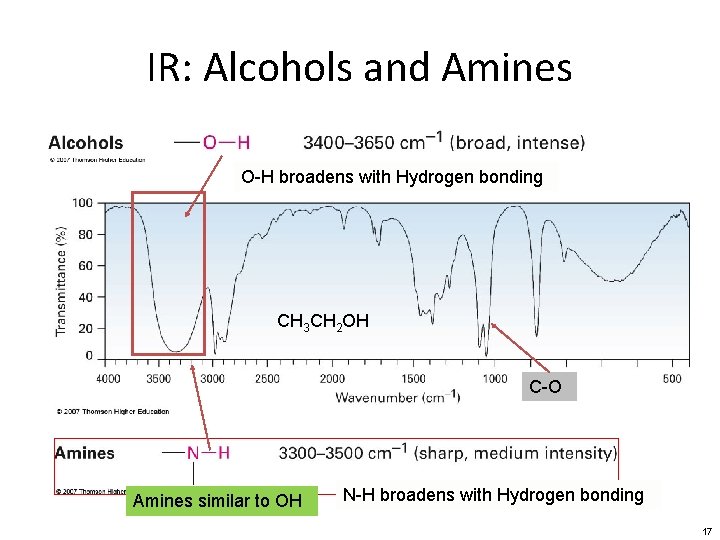
IR: Alcohols and Amines O-H broadens with Hydrogen bonding CH 3 CH 2 OH C-O Amines similar to OH N-H broadens with Hydrogen bonding 17

Question: A strong absorption band of infrared radiation is observed for 1 H 35 Cl at 2991 cm-1. (a) Calculate the force constant, k, for this molecule. (b) By what factor do you expect the frequency to shift if H is replaced by D? Assume the force constant to be unaffected by this substitution. [516. 3 Nm-1; 0. 717]

Hermite polynomial • Recurrence Relation: A Hermite Polynomial at one point can be expressed by neighboring Hermite Polynomials at the same point.

Quantum Mechanical Linear Harmonic Oscillator It is interesting to calculate probabilities Pn(x) for finding a harmonically oscillating particle with energy En at x; it is easier to work with the coordinate q; for n=0 we have:

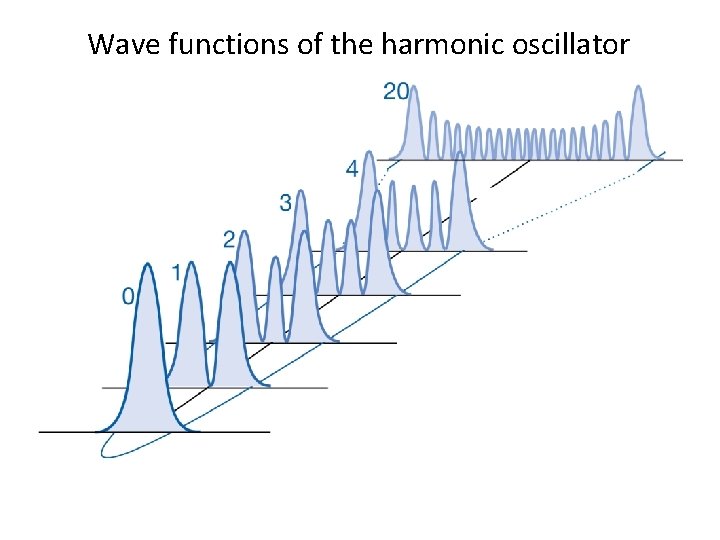
Wave functions of the harmonic oscillator

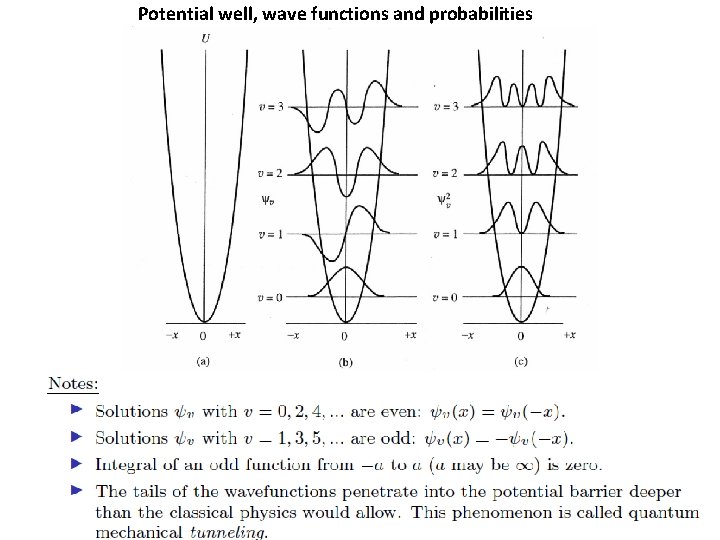
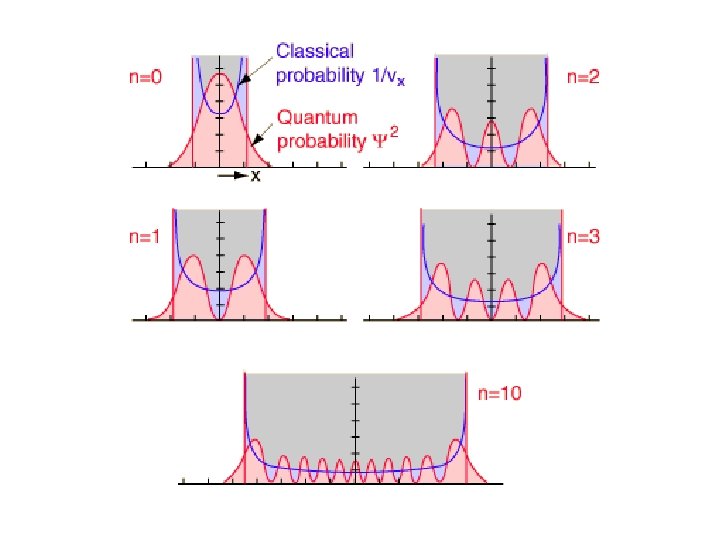
Potential well, wave functions and probabilities

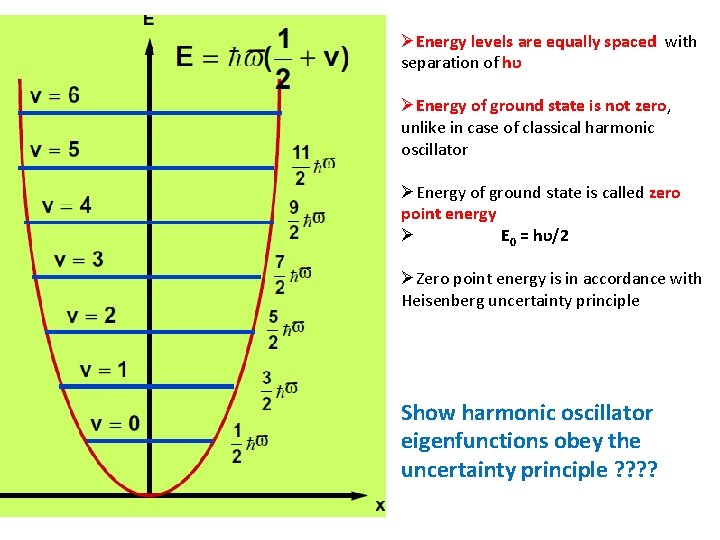
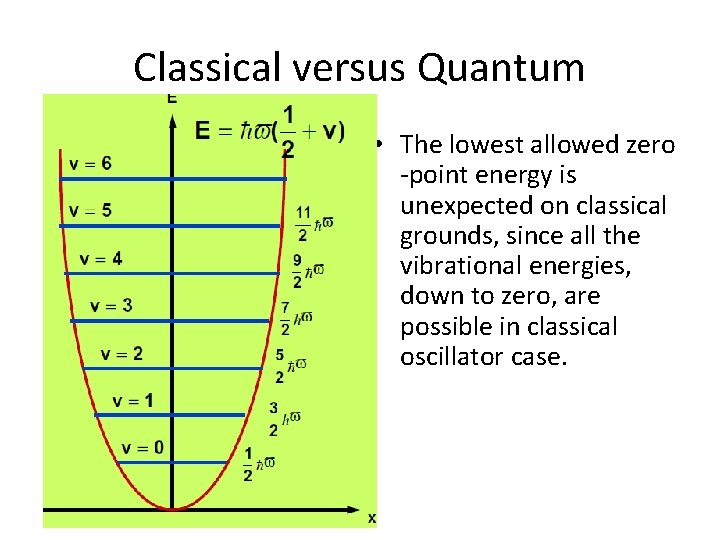
ØEnergy levels are equally spaced with separation of hʋ ØEnergy of ground state is not zero, unlike in case of classical harmonic oscillator ØEnergy of ground state is called zero point energy Ø E 0 = hʋ/2 ØZero point energy is in accordance with Heisenberg uncertainty principle Show harmonic oscillator eigenfunctions obey the uncertainty principle ? ?

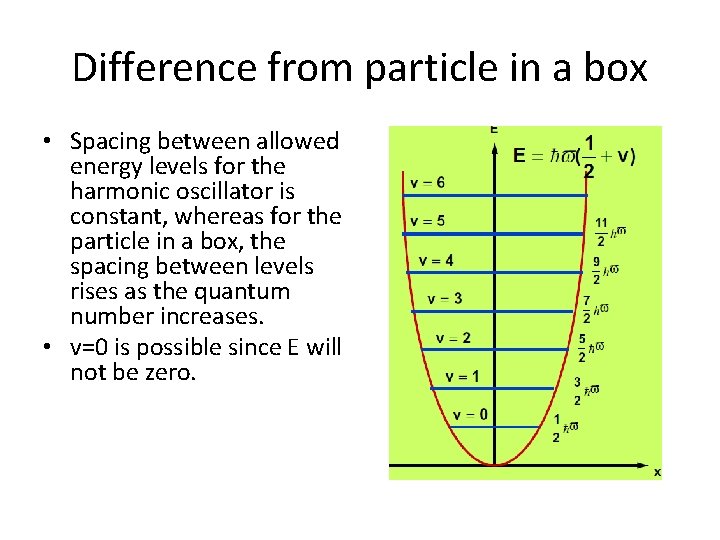
Difference from particle in a box • P. E. varies in a parabolic manner with displacement from the equilibrium and therefore wall of the “box” is not vertical. • In comparison to the “hard” vertical walls for a particle in a box, walls are soft for harmonic oscillator.

Difference from particle in a box • Spacing between allowed energy levels for the harmonic oscillator is constant, whereas for the particle in a box, the spacing between levels rises as the quantum number increases. • v=0 is possible since E will not be zero.

Classical versus Quantum • The lowest allowed zero -point energy is unexpected on classical grounds, since all the vibrational energies, down to zero, are possible in classical oscillator case.

Classical versus Quantum • In quantum harmonic oscillator, wavefunction has maximum in probability at x = 0. Contrast bahaviour with the classic harmonic oscillator, which has a minimum in the probability at x = 0 and maxima at turning points.

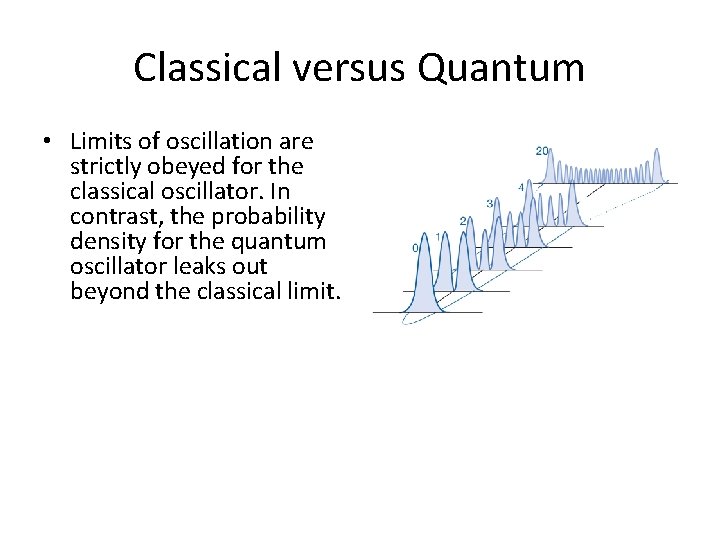
Classical versus Quantum • Limits of oscillation are strictly obeyed for the classical oscillator. In contrast, the probability density for the quantum oscillator leaks out beyond the classical limit.

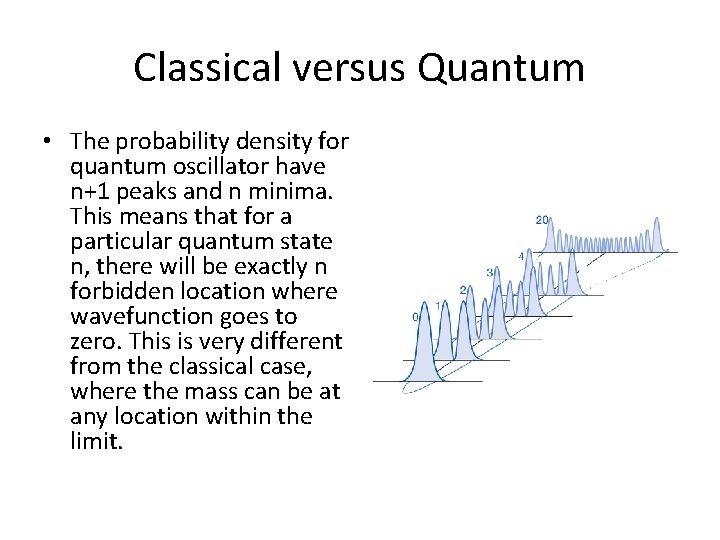
Classical versus Quantum • The probability density for quantum oscillator have n+1 peaks and n minima. This means that for a particular quantum state n, there will be exactly n forbidden location where wavefunction goes to zero. This is very different from the classical case, where the mass can be at any location within the limit.

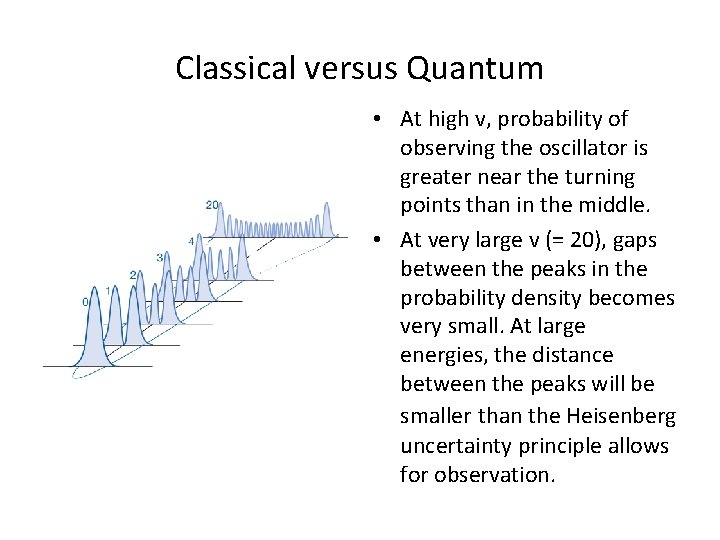
Classical versus Quantum • At high v, probability of observing the oscillator is greater near the turning points than in the middle. • At very large v (= 20), gaps between the peaks in the probability density becomes very small. At large energies, the distance between the peaks will be smaller than the Heisenberg uncertainty principle allows for observation.

Classical versus Quantum • The region for non-zero probability outside classical limits drops very quickly for high energies, so that this region will be unobservable as a result of the uncertainty principle. Thus, the quantum harmonic oscillator smoothly crosses over to become classical oscillator. This crossing over from quantum to classical behaviour was called “Correspondence Principle” by Bohr.