Understanding Limits Limits Limits are the foundation of

Understanding Limits

Limits • Limits are the foundation of calculus • Just like the foundation of a house is essential to the house being built well, limits are the same way • We are building the “house of calculus”

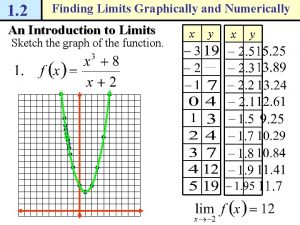
Going where we can’t go…. • Ex. 1 Graph f(x) = x 2. Is there any x-value on this function where you can’t go? • This means the function is continuous. • Note: When I refer to “location”, I am talking about an x-value. When I talk about “point” or “coordinate”, I am talking about the (x, y) pair.

Removable Discontinuity • Ex 2. Graph , go to x = 1 in the table, and see what y value is there. If you cannot get there, what is going on there? • This interruption to the flow of the graph is called a removable discontinuity or hole.

Going where we can’t go…. • There is a need to come up with another method that will circumvent the possibility of going directly to a location, but rather approaching that location from either side of it. • This is the limit • The limit is the y-value that the function approaches as x approaches a value • It is written

One sided limits • How close to edge of the bridge do you need to get in order to tell what is going on there? • What if you were to inch to the edge of the bridge on the other side? Would you be at the same height? • What if the bridge went all the way across? Would you still be at the same height?

One sided limits • The existence or non-existence of the bridge is irrelevant to the existence of the gorge. This is exactly why the limit is so important. It gives us a way to talk about the activity “at” a point whether or not the graph exists there or not

One sided limits • A one-sided limit from the left is written • It means what y value is the function approaching as x gets closer to a from the left • A one-sided limit from the right is written • It means what y value is the function approaching as x gets closer to a from the right

One sided limits • Ex. 3 Let’s say a road is defined by the graph of f(x)=2 x+2. There is a gorge at x=1. We want to know what the y-values are approaching as the x -values are approaching x = 1 from both sides of the x-coordinate of the gorge. Use your calculator to explore. Write the results as onesided limits.

One sided limits • If and only if (Iff) a graph approaches the same y -value from both sides, we say the limit exists. In this case, we’d write the results found above as: • In the road bridge analogy, we say that left road=bridge=right road

Continuity • Stated in words, when a function is continuous at a point, the function value and the limit value are the same.

Example 4 • Discuss the continuity of this fact to find . Use

Example 5 • Discuss the continuity of. Find by using your calculator to find numerically.

Example 5 using algebra instead • From pre-calculus, you should remember there is a way to find a y-value without using your calculator to find it numerically. • It is worth noting that if we were interested in finding the limit at any other value of x, we could use direct substitution, because it is continuous everywhere else.

Example 6 (algebra) • Consider the piecewise function • Find • Is the function continuous at x = -2? • Find • Is the function continuous at x = 2?

Jump discontinuity • When the one-sided limits exist but are different values, we get what is called a jump discontinuity

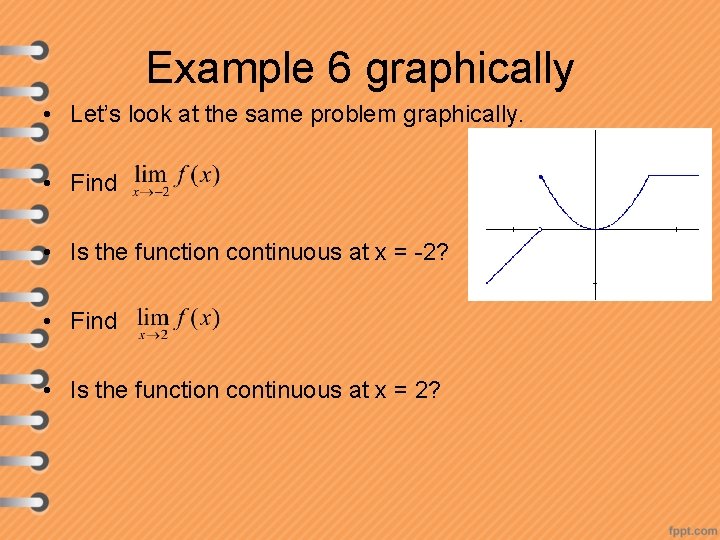
Example 6 graphically • Let’s look at the same problem graphically. • Find • Is the function continuous at x = -2? • Find • Is the function continuous at x = 2?

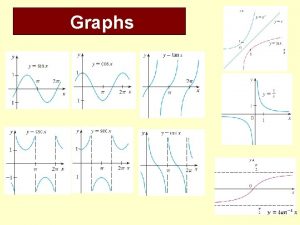
Infinite Discontinuities • We have looked at 2 types of discontinuities – holes and jump. • A third type of discontinuity is vertical asymptotes, officially infinite discontinuities. • The one-sided limits where there is a vertical asymptote will always be either positive or negative infinity

Vertical asymptotes

Example 7 • Evaluate with a graph

One final type of discontinuity • Called an oscillating discontinuity • Ex 8. Graph Zoom in around x=0

Value of limit vs. value of function • When looking for a limit value at x=c, imagine there is a thick vertical line covering up x = c with only the graph showing on either side. You are looking to see what y-values the graph is approaching on either side of x = c. If the graphs appear to be approaching the same y-value, the limit exists and is that y-value. Otherwise the limit doesn’t exist there. • When looking for a function value at x=c, imagine there are shutters covering up on either side of x = c with only the sliver at x = c visible between them. You are now looking for the dot of the piece of the graph that exists in that narrow sliver. If it exists, the yvalue of the dot is the function value f(c).

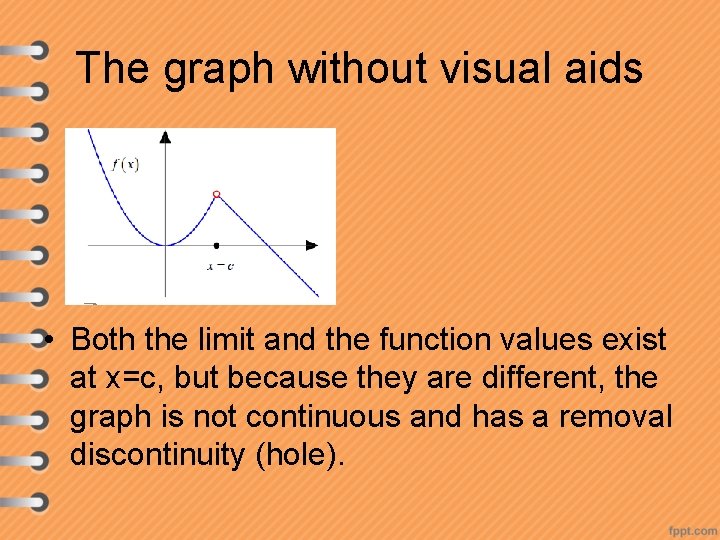
The graph without visual aids • Both the limit and the function values exist at x=c, but because they are different, the graph is not continuous and has a removal discontinuity (hole).

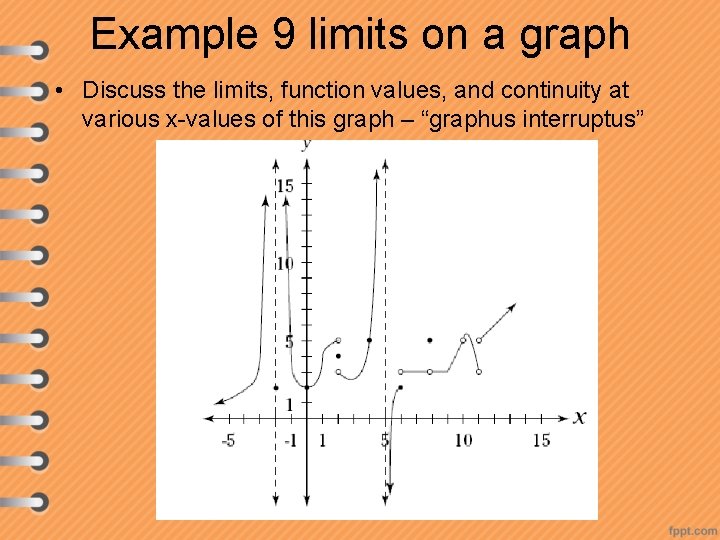
Example 9 limits on a graph • Discuss the limits, function values, and continuity at various x-values of this graph – “graphus interruptus”