LIMITS LIMITS INTRODUCTION LIMITS v Consider the sequences

LIMITS

LIMITS INTRODUCTION

LIMITS v Consider the sequences of values 1. 9, 1. 999, … and 2. 1, 2. 001, … given to a variable x. v The values of x in the first sequence are all less than 2 and approaching 2. In this case we say that x tends to 2 from left and it is denoted by x� 2 -.

LIMITS v The values of x in the second sequence are all greater than 2 and approaching 2. In this case we say that x tends to 2 from right and it is denoted by x� 2+. v If x tends to 2 either from left or from right then we say x tends to 2 and it is denoted by x� 2.

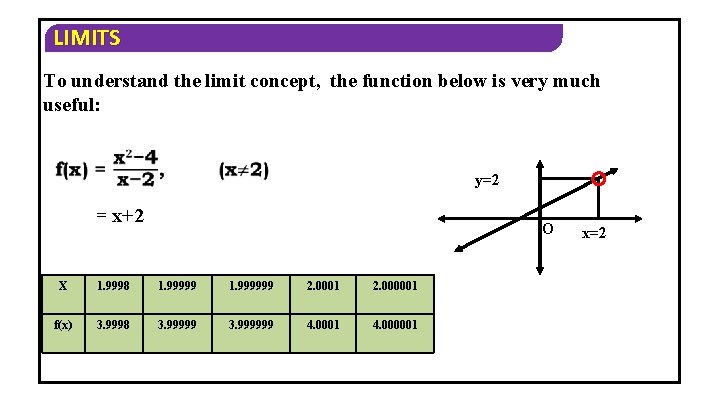
LIMITS To understand the limit concept, the function below is very much useful: y=2 = x+2 O X 1. 9998 1. 999999 2. 0001 2. 000001 f(x) 3. 9998 3. 999999 4. 0001 4. 000001 x=2

LIMITS From the graph we can easily observe that when x approaches to 2 from the left or right, f(x) approaches to 4 When x→ 2, f(x) → 4 or Lt f(x) = 4 x 2 In this the left approach is called left hand limit L. H. L = Lt - f(x) = 4 x 2

LIMITS The right approach is called right hand limit Lt f(x) = 4 R. H. L = x 2 +

LIMITS RIGHT AND LEFT HAND LIMITS We studied the limit of a function f at a given point x=a as the approaching value of f(x) when x tends to ‘a’. Here we note that there are two ways x could approach ‘a’, either from the left of ‘a’ or from the right of ‘a’. This naturally leads to two limits, namely ‘the right hand limit’ and ‘the left hand limit’.

LIMITS

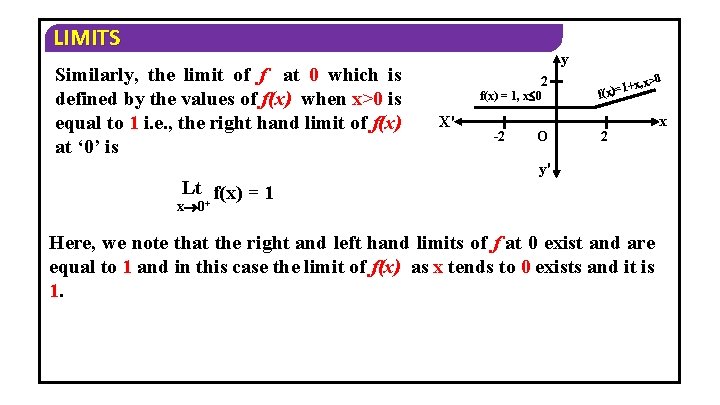
LIMITS Solution We observe that the limit of f at 0 which is defined by the values of f(x) when x<0 is equal to 1 i. e. , the left hand limit of f(x) at ‘ 0’ is Lt f(x) = 1 - x 0

LIMITS Similarly, the limit of f at 0 which is defined by the values of f(x) when x>0 is equal to 1 i. e. , the right hand limit of f(x) at ‘ 0’ is Lt f(x) = 1 + y 2 f(x) = 1, x 0 X' -2 O x, x>0 + 1 = ) f(x 2 y' x 0 Here, we note that the right and left hand limits of f at 0 exist and are equal to 1 and in this case the limit of f(x) as x tends to 0 exists and it is 1. x

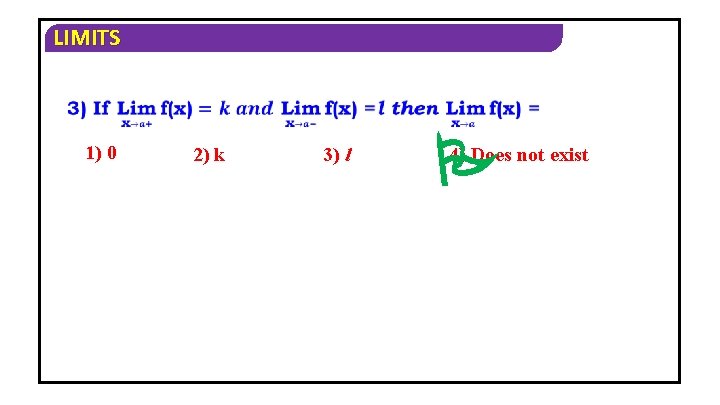
LIMITS MCQs P 1) 0 2) 1 P 2) k 3) 2 3) -k 4) 2 k 4) 3

LIMITS 1) 0 2) k 3) l P 4) Does not exist

LIMITS SOME IMPORTANT DEFINITIONS

LIMITS y Solution (0, 1) x' O x (0, -1) From figure, we observe that Lt f(x) = 1 - y' x 0 Hence, the right and left hand limits of f at 0 are different. We observe that the limit of f(x) as x tends to 0 does not exist.

LIMITS MODULUS OF A REAL NUMBER If x R, then the absolute value or modulus of ‘x’ is denoted by |x| and is defined as follows |x| = x, if x 0 = -x, if x<0

LIMITS STEP FUNCTION The function f: R R defined as f(x) = n where n Z such that n x<n+1, x R is called step function It is denoted by f(x) = [x]

LIMITS Note If x R then [x] = the integral part of x. Lt + [x] = a and x a Lt x a-

LIMITS INTERVALS A subset A of R is said to be an interval if a, b A and x R, a<x<b x A. Let a, b R and a<b. Then 1) (a, b) = {x R, a<x<b} is called open interval 2) [a, b] = {x R, a x b} is called closed interval

LIMITS 3) (a, b] = {x R, a<x b} is called left open right closed interval 4) [a, b) = {x R, a x<b} is called left closed right open interval 5) (a, ) = {x R: x>a} 6) [a, ) = {x R: x a} 7) (- , a) = {x R : x<a} 8) (- , a] = {x R : x a} 9) (- , ) = R

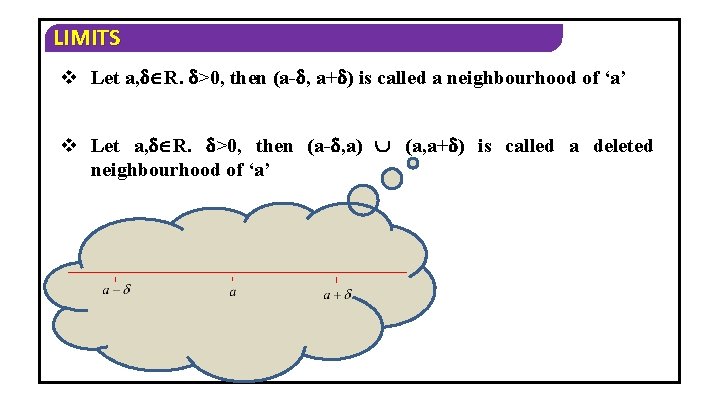
LIMITS v Let a, R. >0, then (a- , a+ ) is called a neighbourhood of ‘a’ v Let a, R. >0, then (a- , a) (a, a+ ) is called a deleted neighbourhood of ‘a’

LIMITS Note If lim f(x) and lim f(x) exist then x a+ x a- i) Lt f(x) = Lt f(a+h) x a+ h 0 ii) Lt f(x) = Lt f(a-h) x a- x a h 0 x a

LIMITS x a x a vi) Lt x a f(x) = 0 and f is negative in a deleted x a neighbourhood of a,

LIMITS

LIMITS SANDWICH THEOREM

LIMITS PROPERTIES OF LIMITS

LIMITS INDETERMINATE FORMS In finding the values of limits, some times we obtain the following forms

LIMITS MCQs 1) 1 1) l 2 P 2) l 3) 0 3) a 4) 3 4) Does not exist

LIMITS 1) 1 P 2) 0 3) -1 4) Does not exist

LIMITS Thank you…