Introduzione allanalisi di sopravvivenza 1 LA CHURN ANALYSIS

Introduzione all’analisi di sopravvivenza 1

LA CHURN ANALYSIS CON L’IMPIEGO DELLE FUNZIONI DI SOPRAVVIVENZA n n Il Lifetime Customer Value (LTV) Il LTV misura il potenziale generatore di profitto, o valore, di un consumatore ed è un concetto guida nel CRM al fine di fornire benefici attrattivi ai consumatori e al tempo stesso massimizzare il profitto dell’impresa. 2

Il Lifetime Customer Value (LTV) n La durata del rapporto può essere stimata con le funzioni di sopravvivenza, con tecniche di data mining, oppure con combinazioni delle due. 3

Funzioni di sopravvivenza n Le funzioni di sopravvivenza generano, per un consumatore i, una hazard function, che descrive la probabilità di defezione al tempo t, indicata con hi(t). 4

Funzioni di sopravvivenza n n La hazard function può essere trasformata in una funzione di sopravvivenza, che rappresenta la probabilità Si(t) che un consumatore sopravviva al tempo t condizionata al fatto che questi sia “vivo” al tempo t-1, ovvero: Si(t) = (Si(t-1) x 1 -hi(t)), con Si(1)=1 5

Sommario n n n Cosa è l’analisi di sopravvivenza Terminologia e struttura dei dati. Funzioni di sopravvivenza/hazard Tecniche di regresione parametriche e semi-parametriche. Introduzione ai metodi Kaplan-Meier (non-parametrici). 6

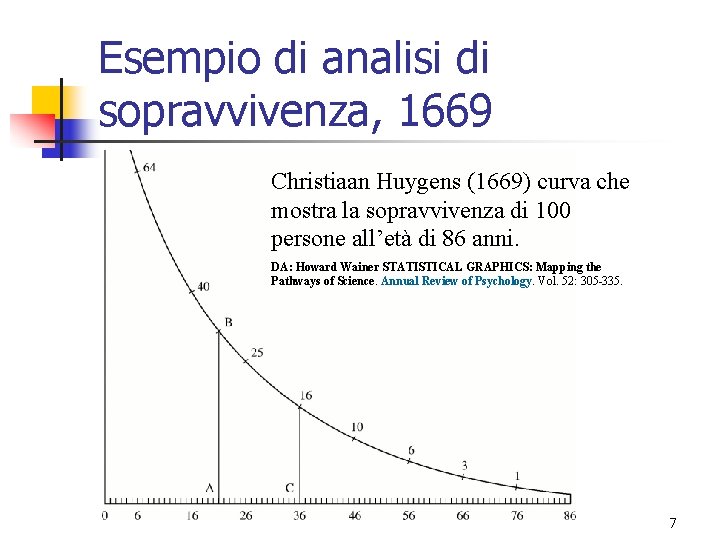
Esempio di analisi di sopravvivenza, 1669 Christiaan Huygens (1669) curva che mostra la sopravvivenza di 100 persone all’età di 86 anni. DA: Howard Wainer STATISTICAL GRAPHICS: Mapping the Pathways of Science. Annual Review of Psychology. Vol. 52: 305 -335. 7

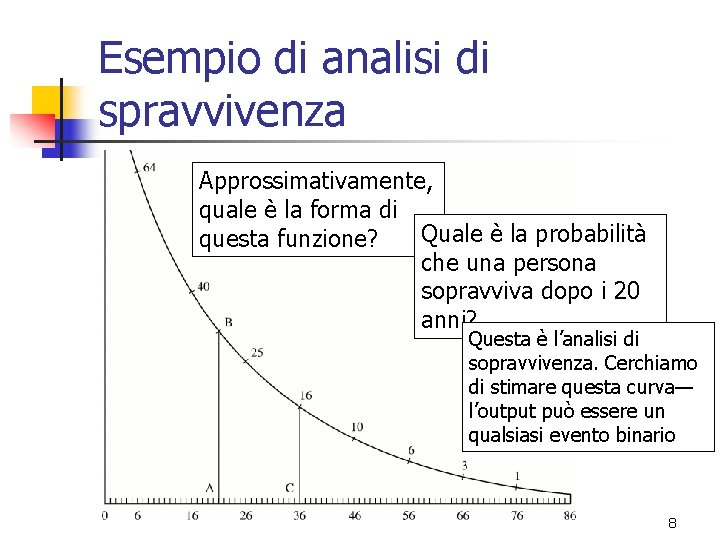
Esempio di analisi di spravvivenza Approssimativamente, quale è la forma di Quale è la probabilità questa funzione? che una persona sopravviva dopo i 20 anni? Questa è l’analisi di sopravvivenza. Cerchiamo di stimare questa curva— l’output può essere un qualsiasi evento binario 8

Cosa è l’analisi di sopravvivenza? n n Metodi statistici per analizzare dati longitudinali sull’occorrenza di eventi. Gli eventi possono essere binary o rappresentare la transizione sopra o sotto la soglia critica di una variabile continua. 9

Obiettivi dell’analisi di sopravvivenza Stimare il tempo all’evento per un gruppo di individui, come il tempo al cambiamento di un fornitore di servizi telefonici per un gruppo di clienti. n Comparare il tempo all’evento tra due o più groppi, ad esempio tra client a cui è stata offerta una promozione o meno. n Stabilire la relazione delle covariate con il tempo all’evento, del tipo: il titolo di studio influenza la durata del rapport di clientela? Nota: tempo all’evento atteso = 1/tasso di incidenza n 10

Perchè usare l’analisi di sopravvivenza? 1. Perchè non comparare le medie del tempo all’evento tra i gruppi usando un test t o la regression lineare? -- si ignorerebbe la censura 2. Perchè non comparare la proporzione di eventi in tra i gruppi usando i risk/odds ratios o la regression logistica? -- si ignorerebbe il tempo 11

Analisi di sopravvivenza: terminologia n n Tempo-all’-evento: Il tempo che intercorre tra l’entrata del soggetto nello studio fino a quando manifesta un particulare “outcome” Censura: I soggetti sono detti sottoposti a censura se se ne perdono le tracce o se escono dallo studio, o se lo studio termina prima che si sia manifestato l’outcome di interesse. Sono contati come “vivi” per il tempo in cui sono stati seguiti nello studio. n Se I dropout sono collegati all’outcome e al trattamento, possono distorcere i risultati. 12

Struttura dei dati Due variabili di outcome : n Variabile tempo: ti = tempo all’evento n Variabile di censura: ci =1 se si è verificato l’evento; ci =0 nessun evento fino al tempo ti 13

Censura a destra (T>t) Esempi comuni n Fine dello studio n Incapacità di seguire il soggetto Sappiamo che il soggetto è “sopravissuto” almeno fino al tempo t. 14

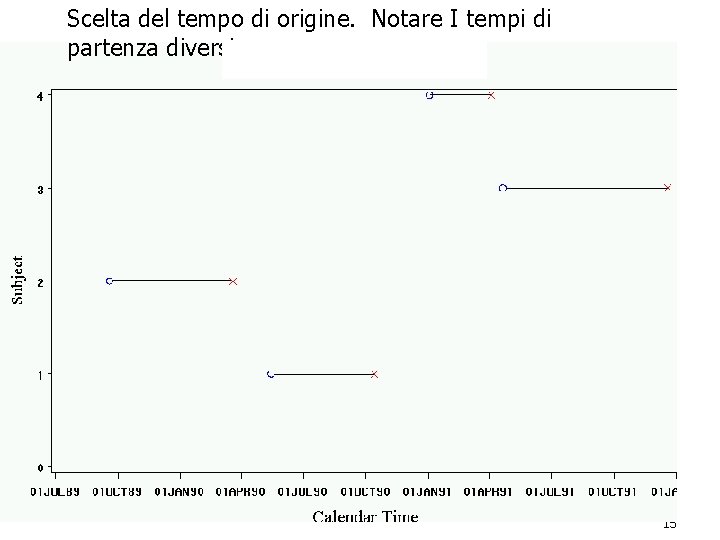
Scelta del tempo di origine. Notare I tempi di partenza diversi. 15

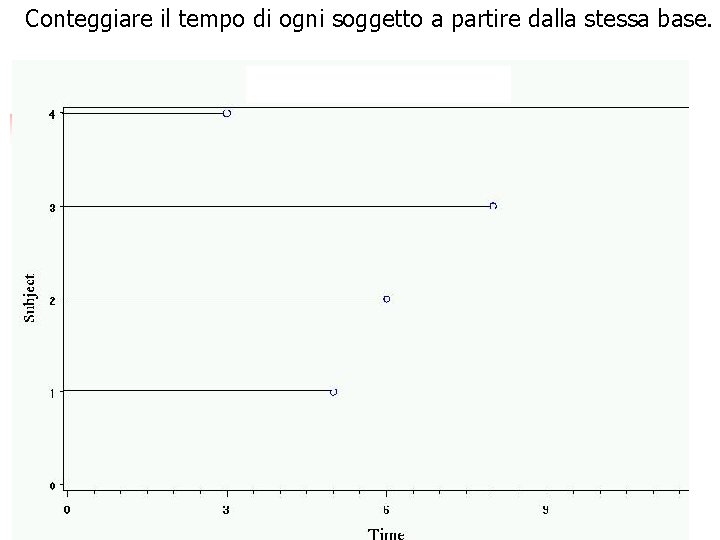
Conteggiare il tempo di ogni soggetto a partire dalla stessa base. 16

Introduzione alle distribuzioni di sopravvivenza n n Ti , il tempo in cui si verifica l’evento per l’individuo i, é una variabile casuale con la propria distribuzione di probabilità. Differenti modelli per i dati di sopravvivenza sono contraddistinti da differenti distribuzioni per Ti. 17

Descrizione delle distribuzioni di sopravvivenza L’ analisi di sopravvivenza parametrica è basata sulle cosiddette distribuzioni del “tempo di attesa” (ad esempio: la distribuzione esponenziale). L’idea é la seguente: Assumiamo che i tempi-all’evento per gli individui nel nostro dataset seguano una distribuzione di probabilità continua (che siamo in grado o meno di specificare matematicamente). Per tutti i possibili tempi Ti dopo la base, vi è una certa probabilità che per un individuo si verificherà l’evento esattamente al tempo Ti. Per esempio, gli esseri umani hanno una certa probabilità di morire alle età 3, 25, 80, and 140: 18

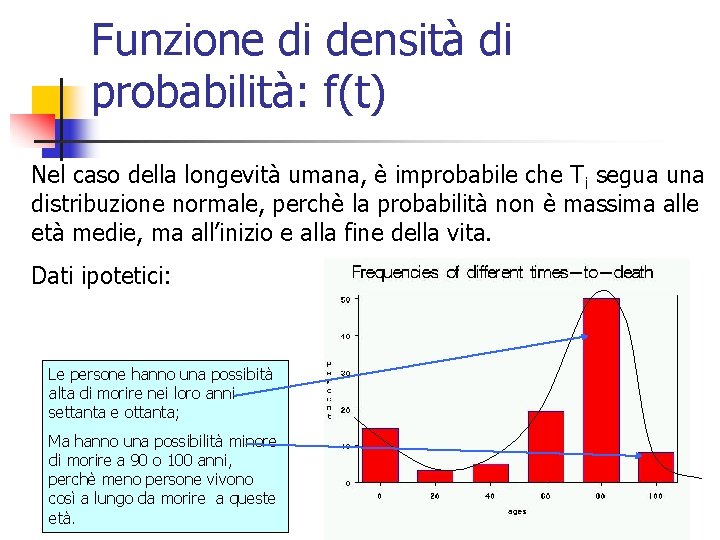
Funzione di densità di probabilità: f(t) Nel caso della longevità umana, è improbabile che T i segua una distribuzione normale, perchè la probabilità non è massima alle età medie, ma all’inizio e alla fine della vita. Dati ipotetici: Le persone hanno una possibità alta di morire nei loro anni settanta e ottanta; Ma hanno una possibilità minore di morire a 90 o 100 anni, perchè meno persone vivono così a lungo da morire a queste età. 19

Funzione di densità di probabilità: f(t) La probabilità che il tempo dell’evento sia esattamente al tempo t (all’interno dell’intero campo di possibilità per t). 20

Funzione di sopravvivenza: 1 F(t) L’obiettivo dell’analisi è di stimare e comparare le esperienze di differenti gruppi. L’esperienza é descritta dalla funzione di sopravvivenza cumulativa: F(t) é la CDF di f(t), ed é “più interessante” di f(t). Esempio: Se t=100 anni, S(t=100) = probabilità di sopravvivere oltre i 100 anni. 21

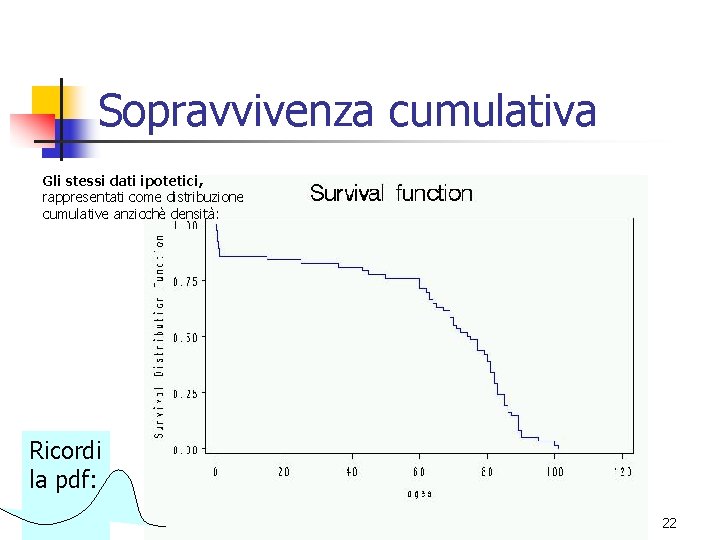
Sopravvivenza cumulativa Gli stessi dati ipotetici, rappresentati come distribuzione cumulative anzicchè densità: Ricordi la pdf: 22

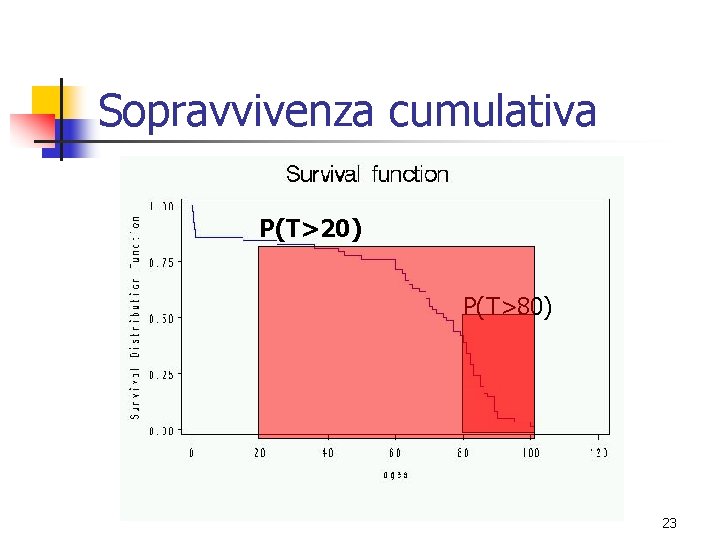
Sopravvivenza cumulativa P(T>20) P(T>80) 23

Funzione di hazard: nuovo concetto Il tasso di hazard é un tasso di incidenza istantaneo. AGES 24

Funzione di hazard In parole: è la probabilità che se tu sopravvivi a t, sarai soggetto all’evento nell’istante successivo. Derivazione (regola di Bayes): 25

Hazard rispetto alla densità L’idea di base è la seguente: n Quando nasci, hai una certa probabilità di morire ad ogni età; questa è la densità di probabilità (equivalente alla probabilità marginale) n n Ad esempio: una donna nata oggi ha, diciamo, una possibilità dell’ 1% di morire a 80 anni. Comunque, se tu sopravvivi per un certo periodo, le tue probabilità cambiano (equivalente alla probabilità condizionata) n Ad esempio, una donna che adesso ha 79 anni ha, diciamo, una possibilità del 5% di morire a 80. 26

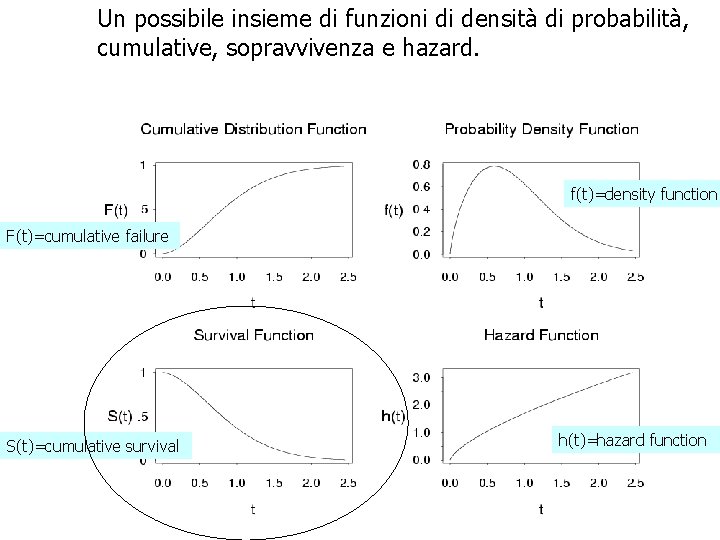
Un possibile insieme di funzioni di densità di probabilità, cumulative, sopravvivenza e hazard. f(t)=density function F(t)=cumulative failure S(t)=cumulative survival h(t)=hazard function 27

Una densità di probabilità che tutti conosciamo: la distribuzione normale n n n Cosa pensi del fatto che la funzione di hazard sia simile ad una distribuzione normale? Pensiamo ad un esempio. Supponiamo che il tempo necessario per completre l’esame di midterm segua una curva normale. Quale è la tua probabilità di finire in un qualsiasi dato momento supposto che stai ancora lavorando? 28

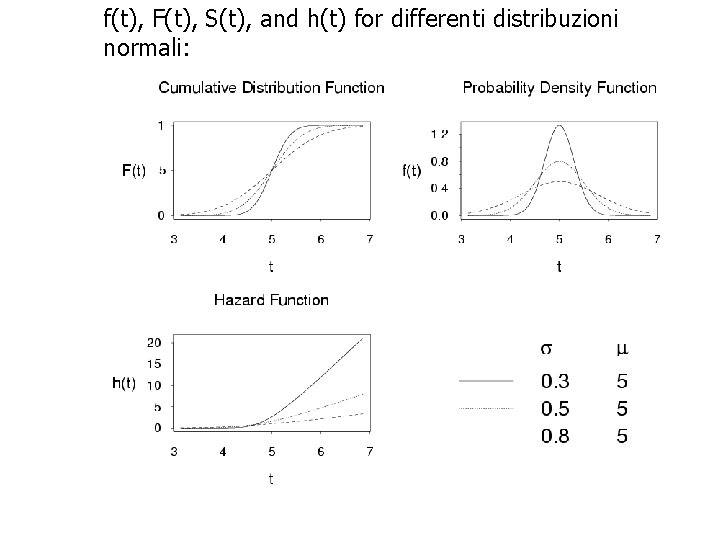
f(t), F(t), S(t), and h(t) for differenti distribuzioni normali: 29

Esempi: funzioni comunemente usate per descrivere la sopravvivenza n n Esponenziale (la funzione di hazard è constante nel tempo, é la più semplice) Weibull (la funzione di hazard function é crescente o decrescente nel tempo) 30

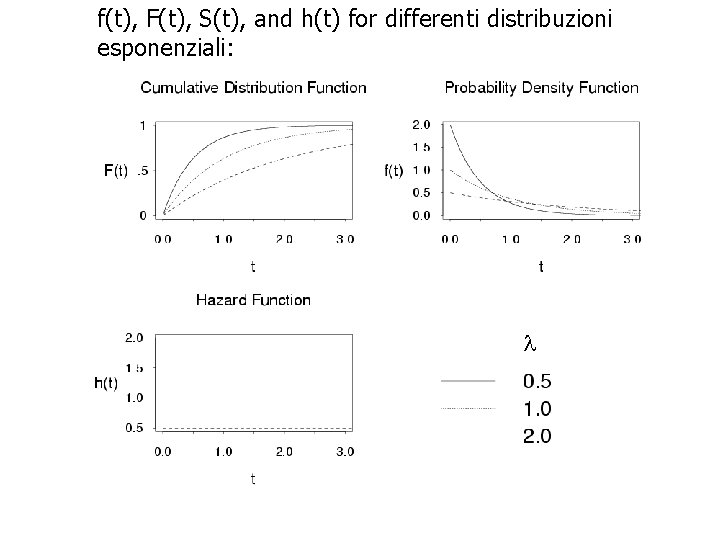
f(t), F(t), S(t), and h(t) for differenti distribuzioni esponenziali: 31

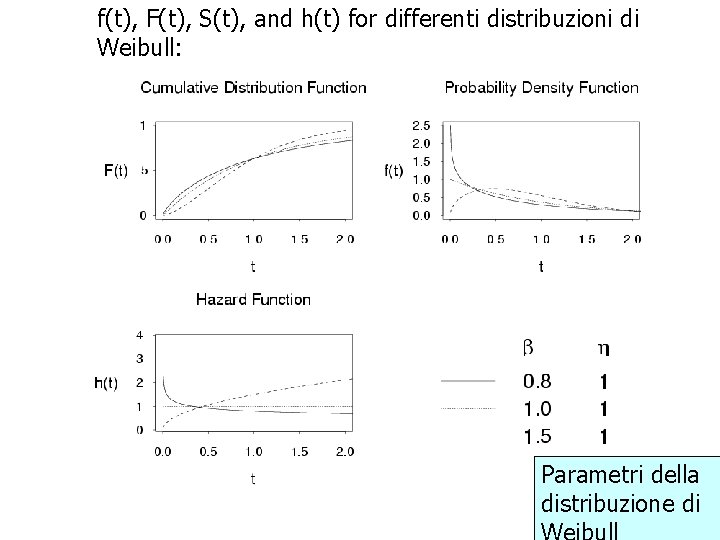
f(t), F(t), S(t), and h(t) for differenti distribuzioni di Weibull: Parametri della distribuzione di 32

Esponenziale Funzione di hazard costante: Funzione di densità esponenziale: Funzione di sopravvivenza: 33

Con i numeri… Why isn’t the cumulative probability of survival just 90% (rate of. 01 for 10 years = 10% loss)? Tasso di incidenza (costante). Probabilità dell’evento all’anno 10. Probabilità di sopravvivere passati 10 anni. (Rischio cumulative fino all’anno 10 é 9. 5%) 34

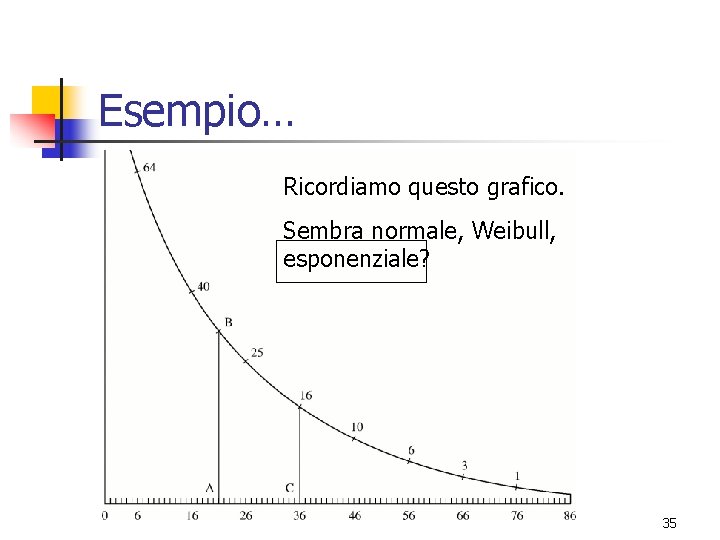
Esempio… Ricordiamo questo grafico. Sembra normale, Weibull, esponenziale? 35

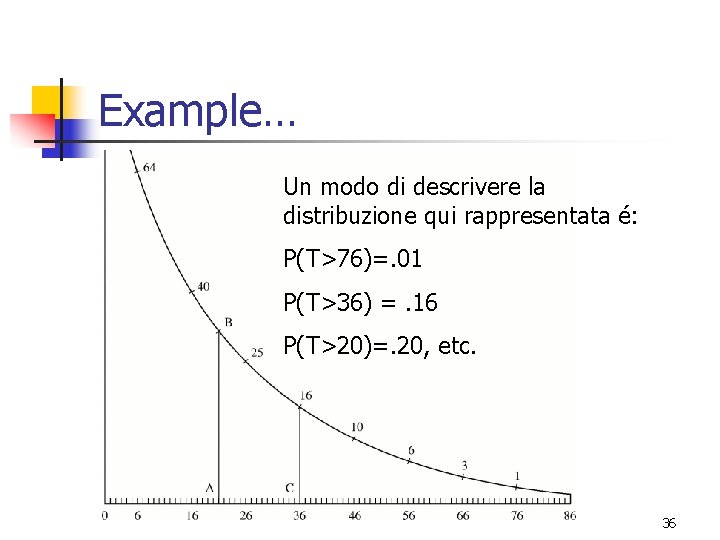
Example… Un modo di descrivere la distribuzione qui rappresentata é: P(T>76)=. 01 P(T>36) =. 16 P(T>20)=. 20, etc. 36

Example… O, più compattamente, cercare di descrivere questa come una funzione esponenziale. Richiamiamo la distribuzione esponenziale: Se T ~ exp (h), allora P(T=t) = he-ht Quando h é un tasso costantr. Qui: Il tempo dell’evento, T ~ exp (Rate) 37

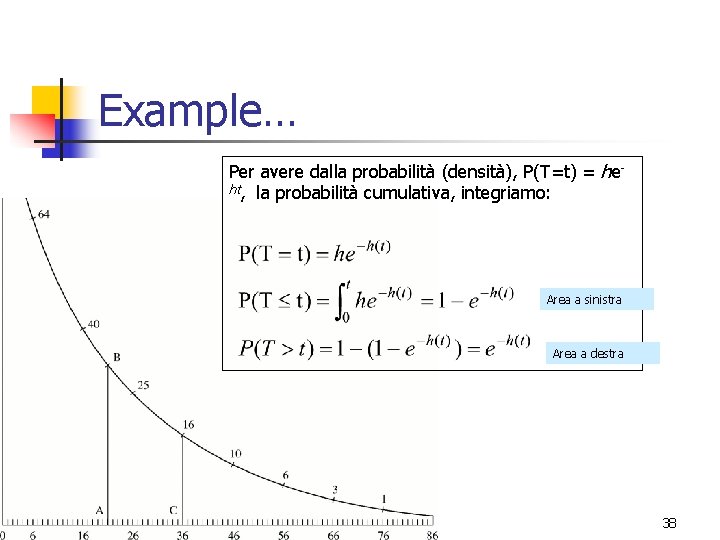
Example… Per avere dalla probabilità (densità), P(T=t) = heht, la probabilità cumulativa, integriamo: Area a sinistra Area a destra 38

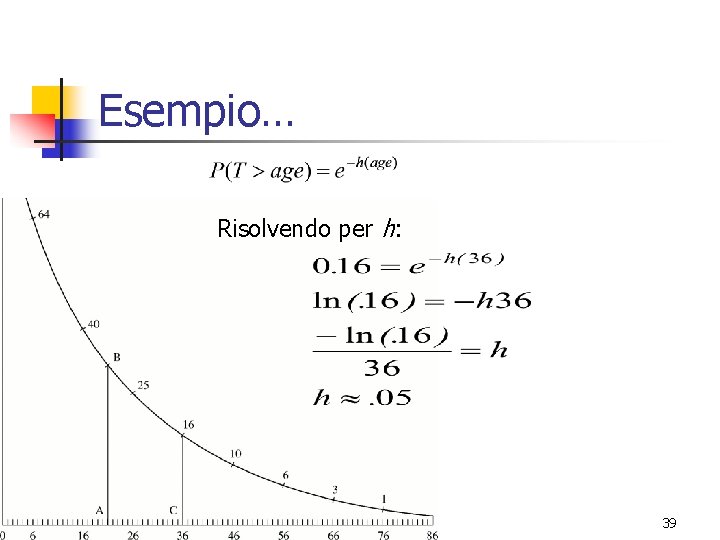
Esempio… Risolvendo per h: 39

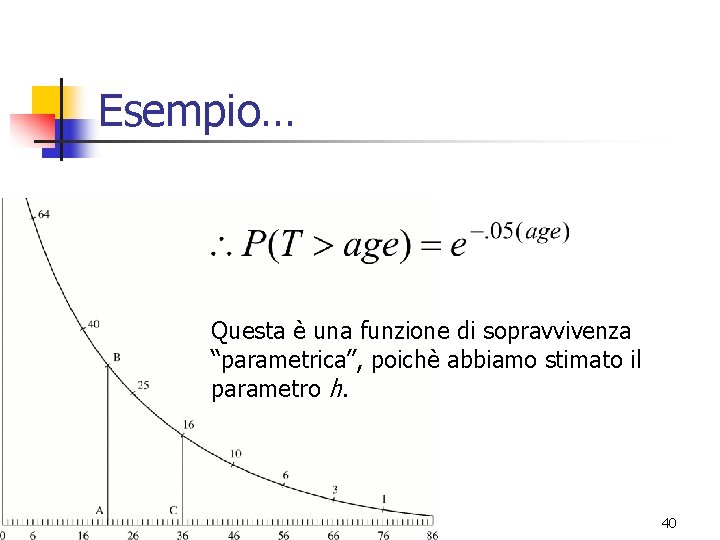
Esempio… Questa è una funzione di sopravvivenza “parametrica”, poichè abbiamo stimato il parametro h. 40

I tassi di hazard possono anche cambiare nel tempo… Esempio: tasso di hazard che aumenta linearmente con il time. 41

Mettiamo in relazione queste funzioni: 42

Ottenere la densità dall’hazard… Esempio: tasso di hazard che cresce linearmente con il tempo. 43

Ottenere la sopravvivenza dall’hazard… 44

Tecniche di regression parametrica n Tecniche di regressione parametrica multivariata: n n Modellare la sottostante funzione di hazard/survival Assumere che la variabile dipendnete (tempoall’evento) segua una distribuzione nota, come la Weibull, l’esponenziale, o la lognormale. Stimare i parametri di queste distribuzioni (ovvero la funzione di hazard base) Stima gli hazard ratio aggiustati per le covariale. n Un hazard ratio è il rapporto of tassi di hazard Molte volte siamo più interessati a paragonare gruppi che a stimare la 45

The model: parametric reg. Components: • A baseline hazard function (which may change over time). • A linear function of a set of k fixed covariates that when exponentiated gives the relative risk. Exponential model assumes fixed baseline hazard that we can estimate. Weibull models the baseline hazard as a function of time. Two parameters (shape and scale) must be estimated to describe the underlying hazard function over time. 46

Il modello Quando esponenziati, i coefficienti dei fattori dai modelli danno gli Componenti: • Una funione di hazard base hazard ratios (rischio relativo). • Una funzione di un insieme di covariate fissate che quando sono esponenziate dà il rischio relativo. 47

Regressione di Cox n n n Semi-parametrica La regression di Cox modella l’effetto delle covariate sul tasso di hazard ma lascia non specificato il tasso base di hazard. E’ anche chiamata regression degli hazards proporzionali NON assume la conoscenza del rischio assoluto. Stima il rischio relativo piuttosto che quello assoluto. 48

Il modello: regression di Cox Componenti: • Una funzione di hazard base chè è lasciata non specificata ma deve essere positiva (=all’hazard quando tutte le covariate sono 0) • Una funzione lineare di un insieme di k covariate fissate che viene poi exponenziata. (=il rischio relativo) Può prendere qualsiasi forma 49

Il modello Il punto è comparare gli hazard rates di individui che hanno covariate differentis: Pertanto, chiamiamo hazards proporzionali: Le funzioni di hazard devono essere strettamente parallele. 50

Introduction to Kaplan-Meier Stima Non-parametrica della funzione di sopravvivenza: Nessuna assunzione matematica (nè sulla sottostante funzione di hazard nè sugli hazard proporzionali). Semplicemente, la probabilità empirica di sopravvivere dopo certe durate nel campione (tenendo conto della censura). 51

Introduzione a Kaplan-Meier n n Stima non parametrica della funzione di sopravvivenza. Comunente usata per descrivere la sopravvivenza della populazione di studio. Comunemente usata per comparare due populazioni di studio. Presentazione grafica intuitiva. 52

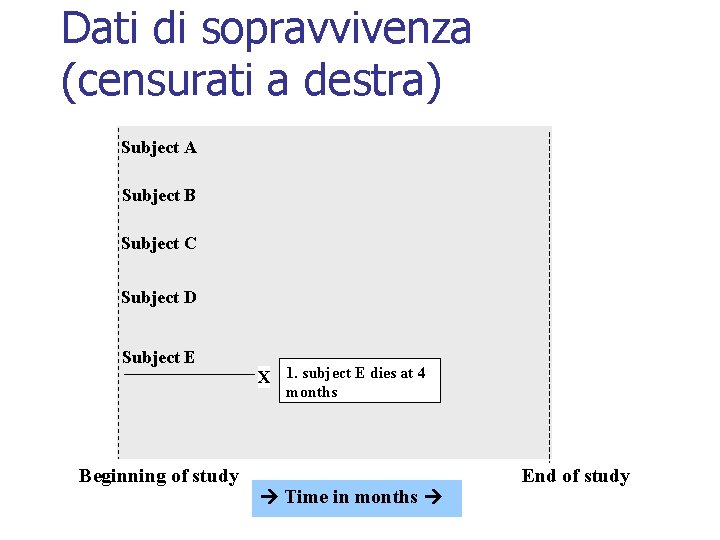
Dati di sopravvivenza (censurati a destra) Subject A Subject B Subject C Subject D Subject E X 1. subject E dies at 4 months Beginning of study Time in months End of study

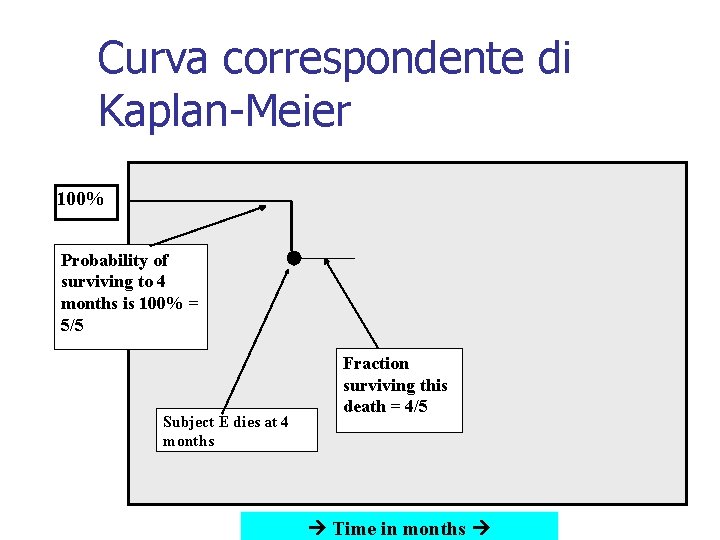
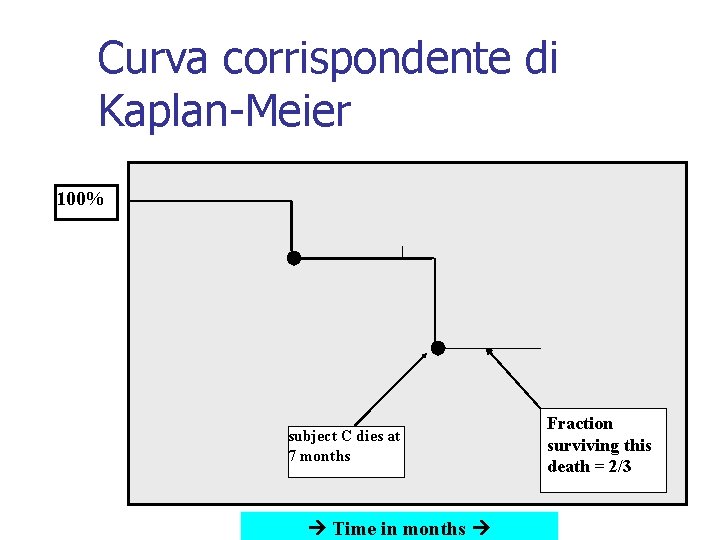
Curva correspondente di Kaplan-Meier 100% Probability of surviving to 4 months is 100% = 5/5 Subject E dies at 4 months Fraction surviving this death = 4/5 Time in months

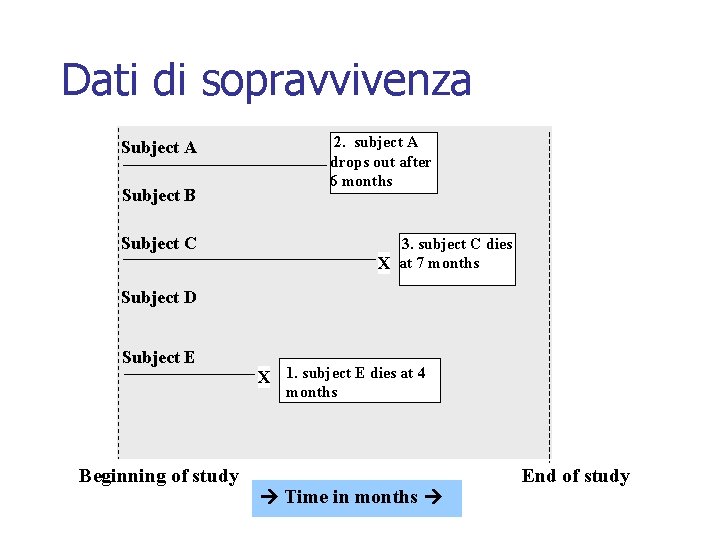
Dati di sopravvivenza Subject A Subject B 2. subject A drops out after 6 months Subject C 3. subject C dies X at 7 months Subject D Subject E X 1. subject E dies at 4 months Beginning of study Time in months End of study

Curva corrispondente di Kaplan-Meier 100% subject C dies at 7 months Time in months Fraction surviving this death = 2/3

Dati di sopravvivenza Subject A Subject B 2. subject A drops out after 6 months Subject C 3. subject C dies X at 7 months Subject D Subject E 4. Subjects B and D survive for the whole year long study period X 1. subject E dies at 4 months Beginning of study Time in months End of study

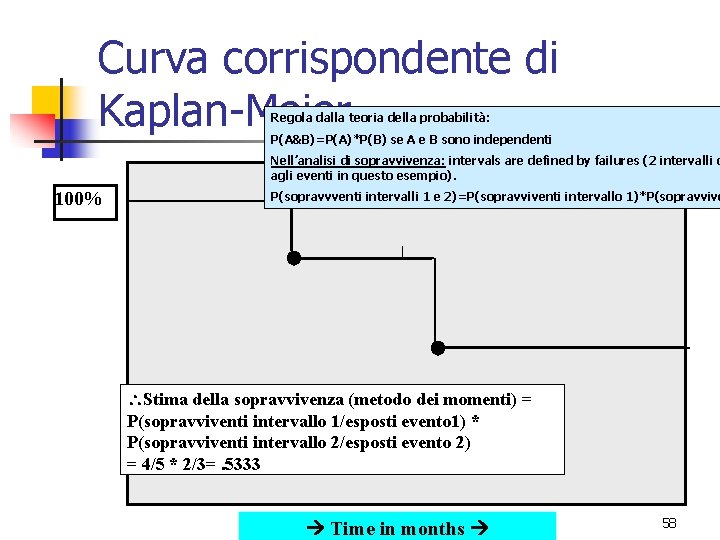
Curva corrispondente di Kaplan-Meier Regola dalla teoria della probabilità: P(A&B)=P(A)*P(B) se A e B sono independenti Nell’analisi di sopravvivenza: intervals are defined by failures (2 intervalli c agli eventi in questo esempio). 100% P(sopravvventi intervalli 1 e 2)=P(sopravviventi intervallo 1)*P(sopravvive Stima della sopravvivenza (metodo dei momenti) = P(sopravviventi intervallo 1/esposti evento 1) * P(sopravviventi intervallo 2/esposti evento 2) = 4/5 * 2/3=. 5333 Time in months 58

La stima prodotto-momento n n La probabilità di sopravviver l’intero anno, tenendo conto della censura = (4/5) (2/3) = 53% NOTARE: 40% (2/5) prchè il drop-out è sopravvissuto almeno una porzione di anno. E <60% (3/5) perchè non sappiamo se il drop -out sia sopravvissuto fino alla fine dell’anno. 59

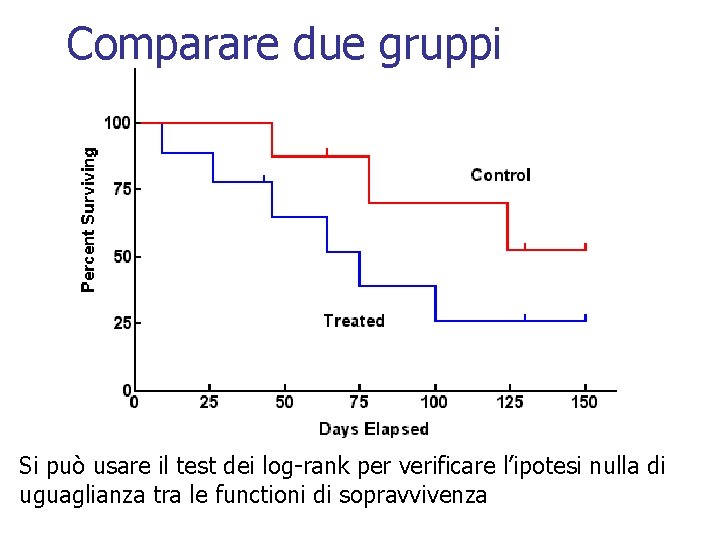
Comparare due gruppi Si può usare il test dei log-rank per verificare l’ipotesi nulla di uguaglianza tra le functioni di sopravvivenza

Caveat n Le stime della sopravvivenza possono essere poco affidabili verso la fine dello studio quando vi sono pochi soggetti a rischio. 61

Limitazioni di Kaplan-Meier • • Principalmente descrittivo Non controlla per le covariate Richiede predittori categorici Non può trattare variabili dipendenti dal tempo 62