Funzioni e derivate Il concetto di derivata Il

















- Slides: 31

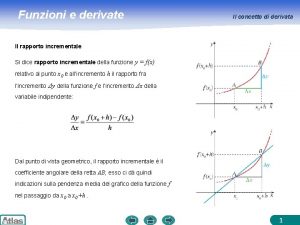
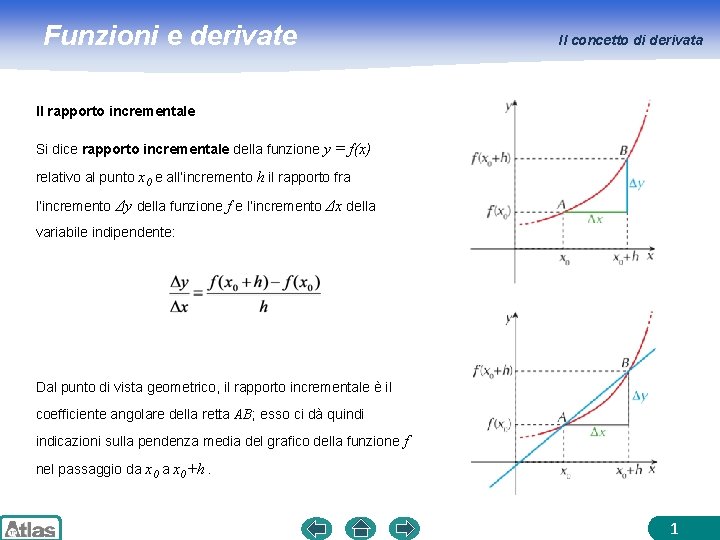
Funzioni e derivate Il concetto di derivata Il rapporto incrementale Si dice rapporto incrementale della funzione y = f(x) relativo al punto x 0 e all’incremento h il rapporto fra l’incremento Δy della funzione f e l’incremento Δx della variabile indipendente: Dal punto di vista geometrico, il rapporto incrementale è il coefficiente angolare della retta AB; esso ci dà quindicazioni sulla pendenza media del grafico della funzione f nel passaggio da x 0+h. 1

Funzioni e derivate Il concetto di derivata ESEMPIO Calcoliamo il rapporto incrementale della funzione di equazione relativo al punto zero e all’incremento h. Per esempio, per nell’intervallo si ha che , quindi la pendenza media del diagramma f(x) è 2

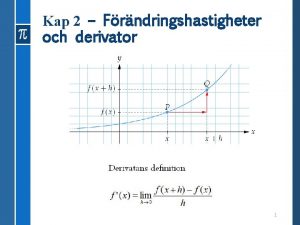
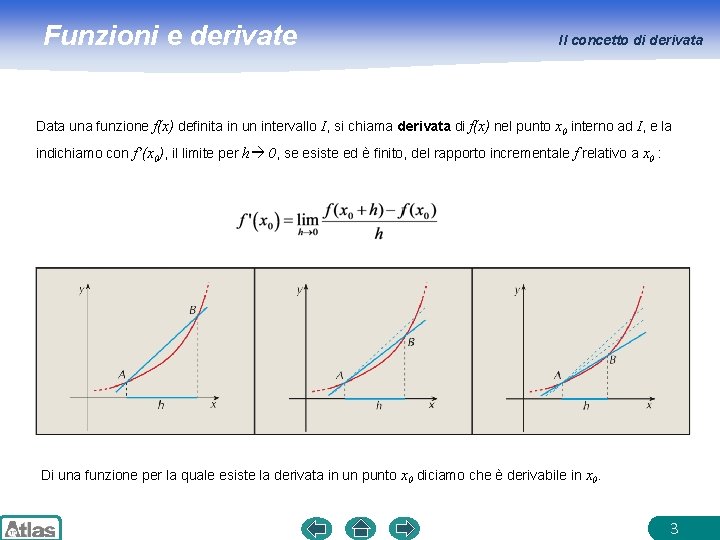
Funzioni e derivate Il concetto di derivata Data una funzione f(x) definita in un intervallo I, si chiama derivata di f(x) nel punto x 0 interno ad I, e la indichiamo con f’(x 0), il limite per h 0, se esiste ed è finito, del rapporto incrementale f relativo a x 0 : Di una funzione per la quale esiste la derivata in un punto x 0 diciamo che è derivabile in x 0. 3

Funzioni e derivate Il concetto di derivata La derivata di una funzione y = f(x) nel punto x 0 si indica con: Dal punto di vista geometrico essa rappresenta il coefficiente angolare della tangente al grafico f(x) nel punto x 0. 4

Funzioni e derivate Il concetto di derivata ESEMPIO Calcoliamo, se esiste, la derivata della funzione Troviamo dapprima il rapporto incrementale relativo a Calcoliamo ora il limite per La funzione nel punto e all’incremento . : di tale rapporto: è quindi derivabile nel punto – 1 e la sua derivata vale – 4. 5

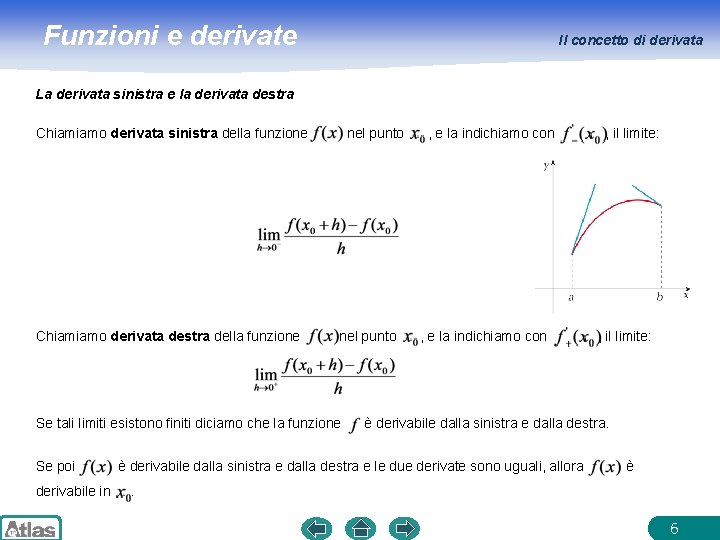
Funzioni e derivate Il concetto di derivata La derivata sinistra e la derivata destra Chiamiamo derivata sinistra della funzione Chiamiamo derivata destra della funzione nel punto Se tali limiti esistono finiti diciamo che la funzione Se poi derivabile in , e la indichiamo con , il limite: è derivabile dalla sinistra e dalla destra e le due derivate sono uguali, allora è . 6

Funzioni e derivate Il concetto di derivata ESEMPIO y Calcoliamo la derivata della funzione In un intorno sinistro di 1 la funzione vale destro vale • in ; in un intorno . La funzione non è quindi derivabile in 1. Calcoliamo la derivata sinistra: 1 x (-1 è il coefficiente angolare della tangente che coincide con la retta di equazione • Calcoliamo la derivata destra: (1 è il coefficiente angolare della tangente che coincide con la retta di equazione La funzione è derivabile dalla sinistra e la sua derivata vale – 1; è derivabile dalla destra e la sua derivata vale 1. 7

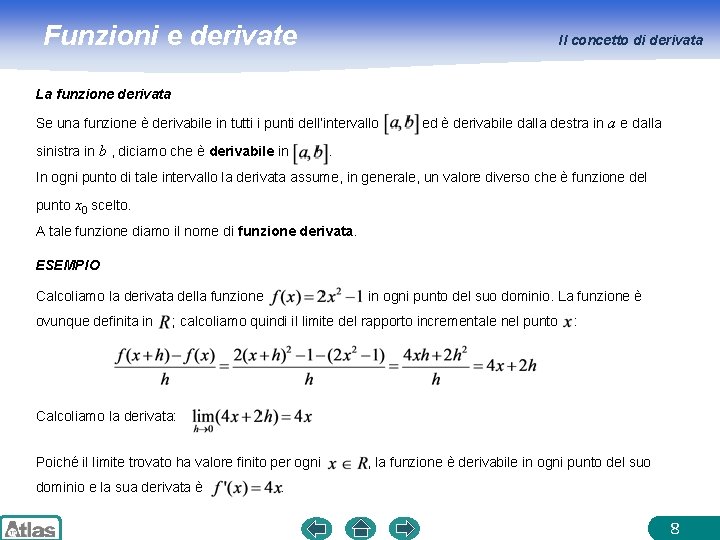
Funzioni e derivate Il concetto di derivata La funzione derivata Se una funzione è derivabile in tutti i punti dell’intervallo sinistra in b , diciamo che è derivabile in ed è derivabile dalla destra in a e dalla . In ogni punto di tale intervallo la derivata assume, in generale, un valore diverso che è funzione del punto x 0 scelto. A tale funzione diamo il nome di funzione derivata. ESEMPIO Calcoliamo la derivata della funzione ovunque definita in in ogni punto del suo dominio. La funzione è ; calcoliamo quindi il limite del rapporto incrementale nel punto : Calcoliamo la derivata: Poiché il limite trovato ha valore finito per ogni dominio e la sua derivata è , la funzione è derivabile in ogni punto del suo . 8

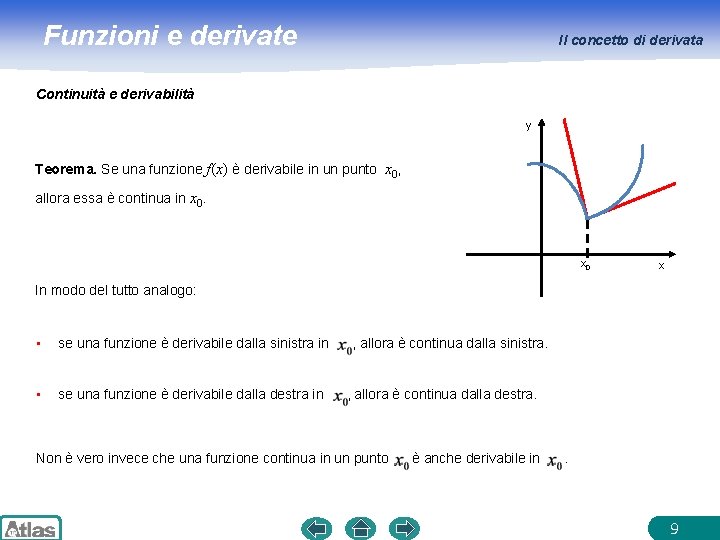
Funzioni e derivate Il concetto di derivata Continuità e derivabilità y Teorema. Se una funzione f(x) è derivabile in un punto x 0, allora essa è continua in x 0 x In modo del tutto analogo: • se una funzione è derivabile dalla sinistra in • se una funzione è derivabile dalla destra in , allora è continua dalla sinistra. , allora è continua dalla destra. Non è vero invece che una funzione continua in un punto è anche derivabile in . 9

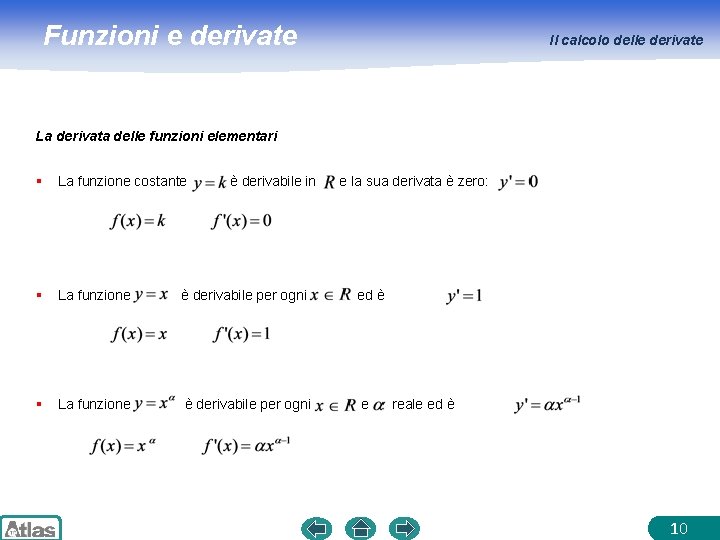
Funzioni e derivate Il calcolo delle derivate La derivata delle funzioni elementari § La funzione costante § La funzione è derivabile per ogni ed è § La funzione è derivabile per ogni e è derivabile in e la sua derivata è zero: reale ed è 10

Funzioni e derivate Il calcolo delle derivate ESEMPI 1. 2. 3. 4. 11

Funzioni e derivate § La funzione è derivabile Il calcolo delle derivate e la sua derivata, se è espresso in radianti, è Analogamente, la derivata di y = cosx è y’ = −sinx § La funzione è derivabile ed è in particolare: § La funzione è derivabile se ed è in particolare: 12

Funzioni e derivate Il calcolo delle derivate La tabella delle derivate delle funzioni fondamentali 13

Funzioni e derivate Il calcolo delle derivate LE REGOLE DI DERIVAZIONE La derivata della somma Teorema. La derivata della somma di due funzioni derivabili è uguale alla somma delle derivate. In simboli: ESEMPI 1. 2. 14

Funzioni e derivate Il calcolo delle derivate La derivata del prodotto Teorema. La derivata del prodotto di due funzioni derivabili è uguale alla derivata della prima funzione per la seconda non derivata, aumentata del prodotto della prima funzione non derivata per la derivata della seconda: In particolare: se k è un numero reale, allora ESEMPI 1. 2. 15

Funzioni e derivate Teorema. Se è una funzione derivabile, la funzione Il calcolo delle derivate è derivabile per ogni tale che sia ed è: La derivata del quoziente Dai due teoremi precedenti possiamo dedurre l’algoritmo per derivare un quoziente. Teorema. Se e sono funzioni entrambe derivabili, per tutti i punti in cui si ha che: 16

Funzioni e derivate Il calcolo delle derivate ESEMPI g’ 1. g 2 f’ g f g’ 2. g 2 17

Funzioni e derivate La derivata di funzioni composte Teorema (di derivazione delle funzioni composte). Sia sia una funzione derivabile nel punto una funzione derivabile in un punto . Allora la funzione è derivabili in e ed è: ESEMPIO Deriviamo la funzione e derivata dell’argomento del logaritmo derivata della funzione logaritmo 18

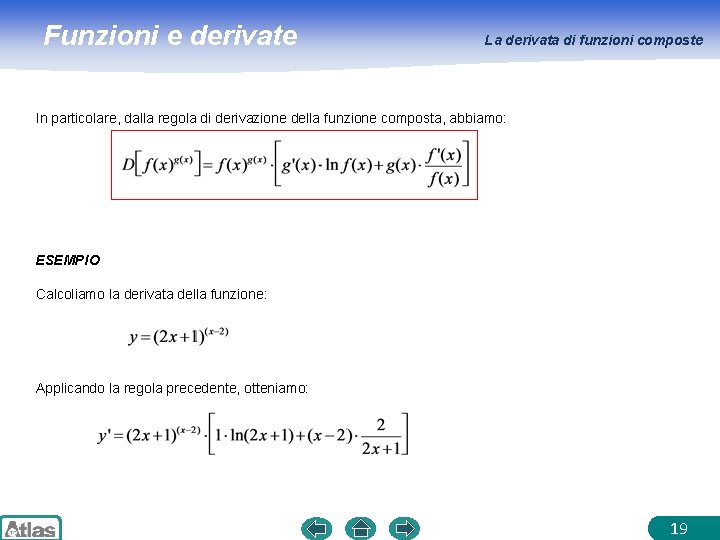
Funzioni e derivate La derivata di funzioni composte In particolare, dalla regola di derivazione della funzione composta, abbiamo: ESEMPIO Calcoliamo la derivata della funzione: Applicando la regola precedente, otteniamo: 19

Funzioni e derivate La derivata della funzione inversa Teorema (di derivazione della funzione inversa). Se in un punto con derivata non nulla, allora anche è invertibile in un intervallo è derivabile nel punto e derivabile ed è: ESEMPIO La funzione è invertibile in Calcoliamo il valore di al quale corrisponde Calcoliamo la derivata della funzione ; calcoliamo la derivata della funzione inversa nel punto . : e valutiamola in : Applicando il teorema: 20

Funzioni e derivate La derivata della funzione inversa Dal teorema precedente possiamo dedurre le derivate delle funzioni inverse di quelle goniometriche. 21

Funzioni e derivate La derivata della funzione inversa ESEMPIO� Calcoliamo la derivata della funzione Si tratta della funzione composta . con Applichiamo la regola di derivazione: derivata dell’argomento dell’arctan derivata della funzione arctan 22

Funzioni e derivate Le rette tangenti e le rette normali Se una funzione è derivabile in un punto x 0 : • il coefficiente angolare della retta tangente è f’(x 0) • il coefficiente angolare della retta normale è se f’(x 0) ≠ 0 La retta tangente ha quindi equazione: La retta normale ha equazione: 23

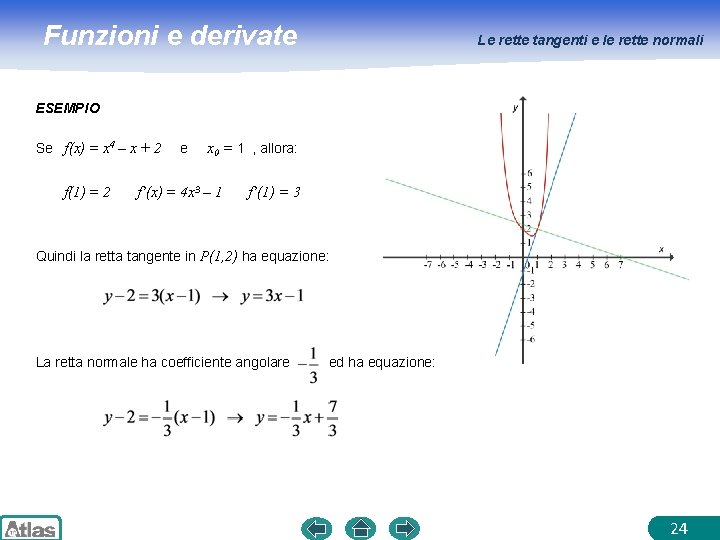
Funzioni e derivate Le rette tangenti e le rette normali ESEMPIO Se f(x) = x 4 – x + 2 f(1) = 2 e x 0 = 1 , allora: f’(x) = 4 x 3 – 1 f’(1) = 3 Quindi la retta tangente in P(1, 2) ha equazione: La retta normale ha coefficiente angolare ed ha equazione: 24

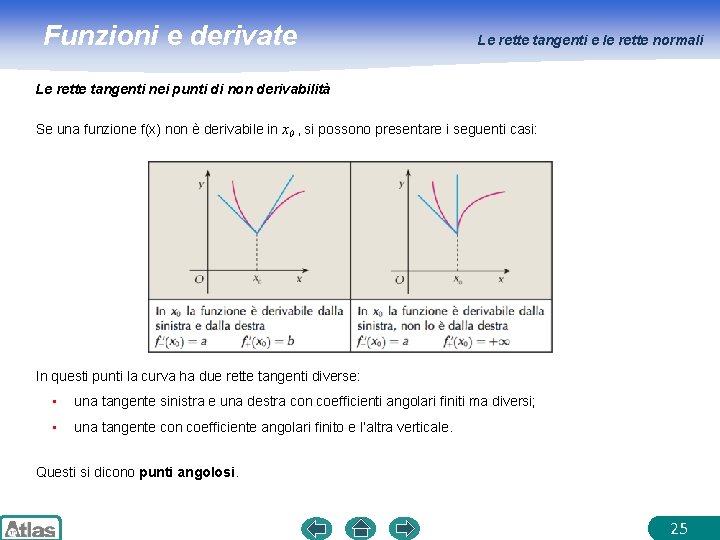
Funzioni e derivate Le rette tangenti e le rette normali Le rette tangenti nei punti di non derivabilità Se una funzione f(x) non è derivabile in x 0 , si possono presentare i seguenti casi: In questi punti la curva ha due rette tangenti diverse: • una tangente sinistra e una destra con coefficienti angolari finiti ma diversi; • una tangente con coefficiente angolari finito e l’altra verticale. Questi si dicono punti angolosi. 25

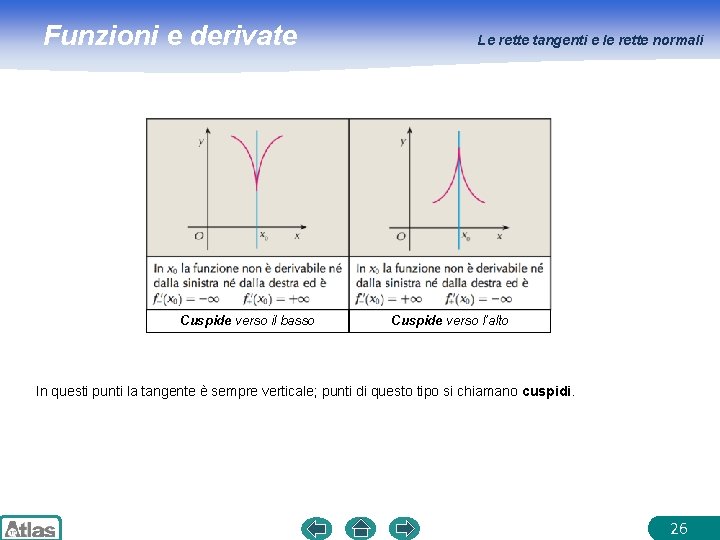
Funzioni e derivate Cuspide verso il basso Le rette tangenti e le rette normali Cuspide verso l’alto In questi punti la tangente è sempre verticale; punti di questo tipo si chiamano cuspidi. 26

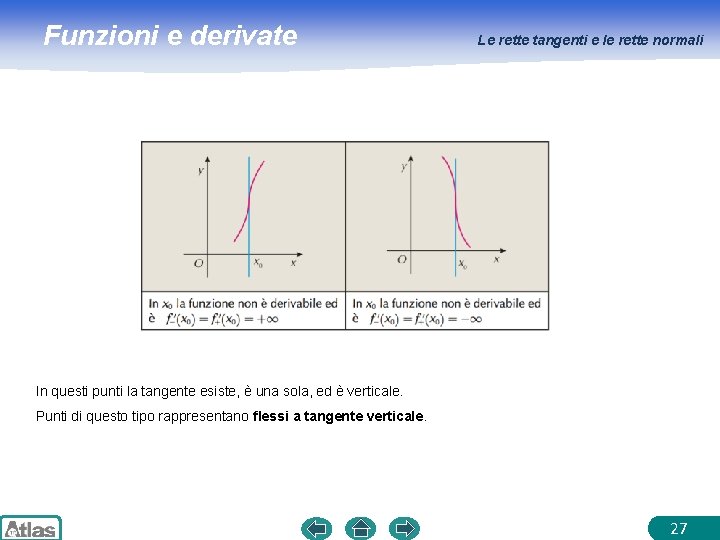
Funzioni e derivate Le rette tangenti e le rette normali In questi punti la tangente esiste, è una sola, ed è verticale. Punti di questo tipo rappresentano flessi a tangente verticale. 27

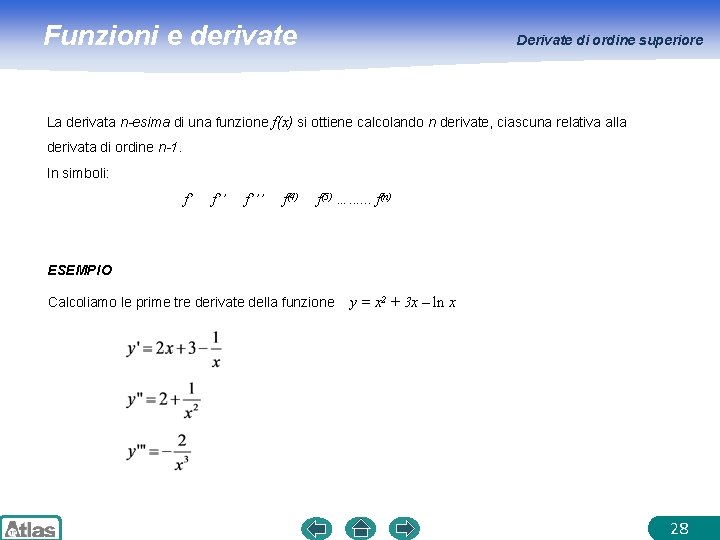
Funzioni e derivate Derivate di ordine superiore La derivata n-esima di una funzione f(x) si ottiene calcolando n derivate, ciascuna relativa alla derivata di ordine n-1. In simboli: f’ f’’’ f(4) f(5) …. . . f(n) ESEMPIO Calcoliamo le prime tre derivate della funzione y = x 2 + 3 x – ln x 28

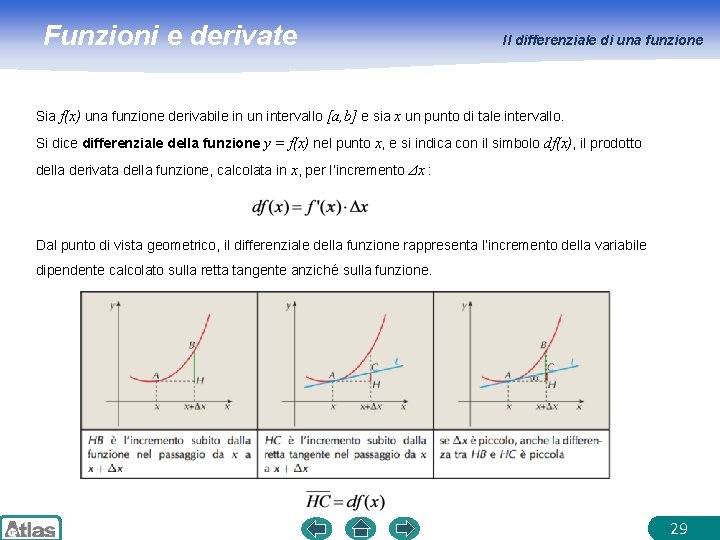
Funzioni e derivate Il differenziale di una funzione Sia f(x) una funzione derivabile in un intervallo [a, b] e sia x un punto di tale intervallo. Si dice differenziale della funzione y = f(x) nel punto x, e si indica con il simbolo df(x), il prodotto della derivata della funzione, calcolata in x, per l’incremento Δx : Dal punto di vista geometrico, il differenziale della funzione rappresenta l’incremento della variabile dipendente calcolato sulla retta tangente anziché sulla funzione. 29

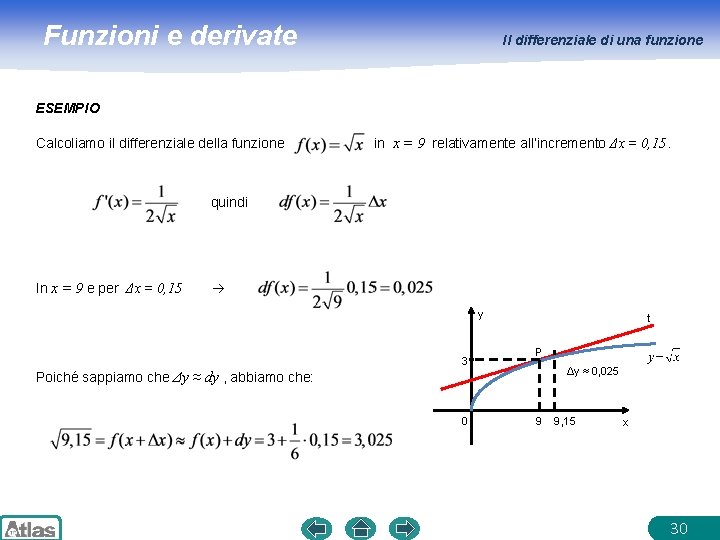
Funzioni e derivate Il differenziale di una funzione ESEMPIO Calcoliamo il differenziale della funzione in x = 9 relativamente all’incremento Δx = 0, 15. quindi In x = 9 e per Δx = 0, 15 y 3 t P Δy ≈ 0, 025 Poiché sappiamo che Δy ≈ dy , abbiamo che: 0 9 9, 15 x 30

Funzioni e derivate Il differenziale di una funzione Il differenziale e la derivata Calcoliamo il differenziale della funzione f(x) = x : df(x) = 1 · Δx dx = Δx Possiamo allora riscrivere il differenziale di una funzione f qualsiasi nella forma: df(x) = f’(x)dx da cui ricaviamo Quindi: la derivata di una funzione f(x) è il rapporto tra il differenziale della funzione f e il differenziale della variabile indipendente x. 31
 Quando una funzione è derivabile
Quando una funzione è derivabile Derivati dalla parola pane
Derivati dalla parola pane Teorema di leibniz newton
Teorema di leibniz newton Retta tangente
Retta tangente Punto di flesso orizzontale
Punto di flesso orizzontale Regole derivazione
Regole derivazione Vad är f(x)
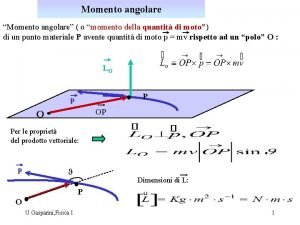
Vad är f(x) Momento angolare
Momento angolare Derivata di una parabola
Derivata di una parabola Bestäm rektangelns maximala area med hjälp av derivatan
Bestäm rektangelns maximala area med hjälp av derivatan Gabriella puppo
Gabriella puppo La lacrima di ghiaccio
La lacrima di ghiaccio Integrale operazione inversa della derivata
Integrale operazione inversa della derivata Iis marchesi
Iis marchesi Derivate notevoli
Derivate notevoli Fungsi turunan diferensial
Fungsi turunan diferensial Definizione di bisogno
Definizione di bisogno Grandezze unitarie esempi
Grandezze unitarie esempi Esempio di operativizzazione di un concetto
Esempio di operativizzazione di un concetto Liceo scientifico mascalucia
Liceo scientifico mascalucia Il concetto di bisogno
Il concetto di bisogno Iis concetto marchesi
Iis concetto marchesi Luogo di posizione di egual differenza d'azimut
Luogo di posizione di egual differenza d'azimut Gheorghe derivate
Gheorghe derivate Mezi si extremi
Mezi si extremi Piano cartesiano e la retta
Piano cartesiano e la retta Derivation example
Derivation example Derivate definition
Derivate definition Concetto filogenetico di specie
Concetto filogenetico di specie Coala de autor
Coala de autor Cateto etimologia
Cateto etimologia Concetto commerciale
Concetto commerciale