Generaliti Autor Profesor IOAN AIACOBOAIE coala Emil Racovi

Generalităţi Autor Profesor IOAN AIACOBOAIE Şcoala “Emil Racoviţă” Oneşti

Rapoarte Definiţie ●Fie a şi b două numere dintr-o mulţime de numere astfel încât b≠ 0; ►Prin raportul numerelor a şi b se înţelege câtul neefectuat dintre a şi b scris sub forma a ; ( b ≠ 0 ) b Exemplu Raportul dintre 3 şi 5 este 3 5 ; Raportul dintre 0, 25 şi 1, (6) este 0, 25 1, (6) Raportul a două mărimi de acelaşi fel este raportul mărimilor lor, ambele mărimi fiind exprimate în aceeaşi unitate de măsură Exemplu Dacă dimensiunile unei săli dreptunghiulare sunt: L=9 m, l=6 m , atunci putem forma rapoartele: L = 9 m = l 6 m 9 ; 6 l = 6 L 9

Valoarea unui raport. ►Valoarea unui raport este câtul efectuat dintre numărătorul şi numitorul raportului Astfel, valorile rapoartelor de mai sus sunt: 2 3 = 3 9 = = 1, 5 ; 2 6 0, (6) Egalitatea rapoartelor Spunem că două rapoarte sunt egale dacă au valorile egale. Dacă a = k 1 ; b c = k 2 d şi k 1=k 2 c a b= d

Proporţii O egalitate între două rapoarte se numeşte proporţie. Definiţie Forma generală a unei proporţii este: a c = b d a, b, c, d, sunt termemii proporţiei a şi d se numesc termeni extremi iar b şi c se numesc termeni medii (mezi) ►Proprietatea fundamentală a proporţiilor În orice proporţie, produsul extremilor este egal cu produsul mezilor. a c b = a • d d = b • c O egalitate între două rapoarte ( o proporţie ) se poate scrie în mod echivalent sub forma unei egalităţi între două produse de câte doi factori şi reciproc: Exemplu Egalitatea evidentă: 4 16 = 2 8 ; 4 • 8=16 • 2 Analog, se poate scrie în mod echivalent ca proporţie: 3 • x=2 • y x 2 = y 3

Aflarea unui termen necunoscut dintr-o proporţie x Fie proporţia: x • d=b • c b şi deci: = c d ; Din proprietatea fundamentală avem: x= b • c d ; x este un extrem necunoscut. Pentru a afla un extrem necunoscut împărţim produsul mezilor la extremul cunoscut. Din proporţia a b = y d rezultă y= b • y=a • d şi avem : a • d ; y este un mez necunoscut. b Pentru a afla un termen mediu (mez) necunoscut împărţim produsul extremilor la mezul cunoscut.

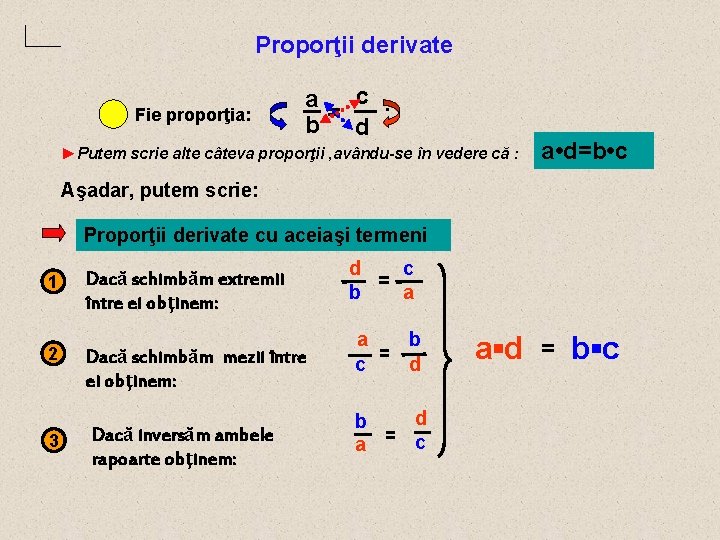
Proporţii derivate Fie proporţia: c a b= d ; ►Putem scrie alte câteva proporţii , avându-se în vedere că : a • d=b • c Aşadar, putem scrie: Proporţii derivate cu aceiaşi termeni 1 2 3 Dacă schimbăm extremii între ei obţinem: Dacă schimbăm mezii între ei obţinem: Dacă inversăm ambele rapoarte obţinem: d c = b a a = c b d d b a = c a▪d = b▪c

Proporţii derivate cu termeni schimbaţi Dacă adunăm (sau scădem) la numărătorii ambelor rapoarte numitorii obţinem tot nişte proporţii a b = c a±b d b = c±d d Dacă adunăm(sau scădem) la numitorii ambelor rapoarte numărătorii obţinem tot nişte proporţii a a c c = = b d a±b c±d Dacă înmulţim (sau împărţim) numărătorii ambelor rapoarte cu acelaşi număr nenul, obţinem tot o proporţie. Aceeaşi transformare este valabilă şi în cazul numitorilor. a • n c • n a: n c: n Dacă n≠ 0 , atunci : = ; = b d În general, transformările pe care le producem unuia dintre rapoartele unei proporţii trebuie să le facem şi celuilalt raport şi obţinem noi proporţii. D e exemplu : În prealabil, ne asigurăm că operaţiile a+b a-b = c+d c-d ! ce trebuiesc efectuate sunt posibile în mulţimea de numere respectivă !

Proprietate importantă Raportul dintre suma (diferenţa) numărătorilor şi suma (diferenţa) numitorilor unei proporţii este egal cu fiecare dintre cele două rapoarte care alcătuiesc acea proporţie. a = c a±c = d b b±d