Momento angolare Momento angolare o momento della quantit

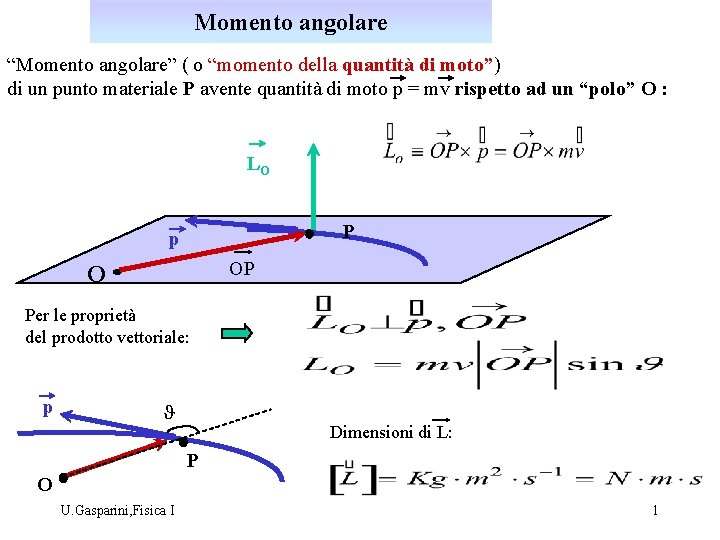
Momento angolare “Momento angolare” ( o “momento della quantità di moto”) di un punto materiale P avente quantità di moto p = mv rispetto ad un “polo” O : LO P p OP O Per le proprietà del prodotto vettoriale: p J Dimensioni di L: P O U. Gasparini, Fisica I 1

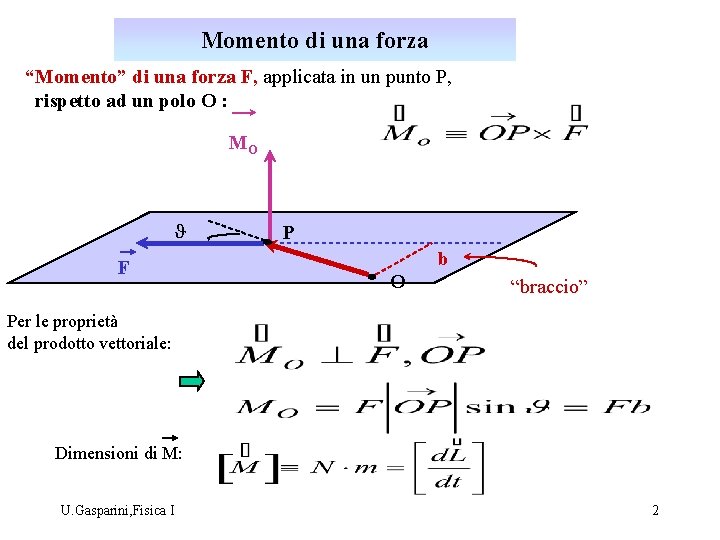
Momento di una forza “Momento” di una forza F, applicata in un punto P, rispetto ad un polo O : MO J F P b O “braccio” Per le proprietà del prodotto vettoriale: Dimensioni di M: U. Gasparini, Fisica I 2

Momento di una forza (II) Cambiando il polo rispetto al quale si calcola il momento di una forza: Analogamente, per il momento angolare: Se si hanno più forze applicate in uno stesso punto P, il momento risultante dei singoli momenti è uguale al momento della forza risultante applicata in P : O P U. Gasparini, Fisica I R 3

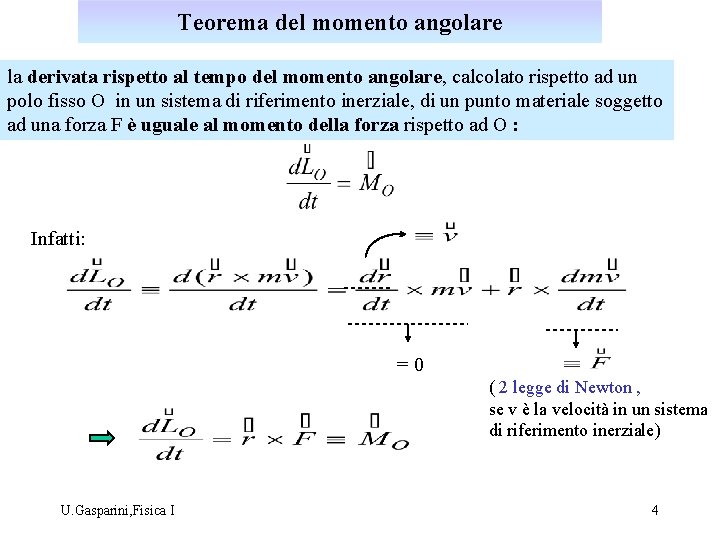
Teorema del momento angolare la derivata rispetto al tempo del momento angolare, calcolato rispetto ad un polo fisso O in un sistema di riferimento inerziale, di un punto materiale soggetto ad una forza F è uguale al momento della forza rispetto ad O : Infatti: =0 ( 2 legge di Newton , se v è la velocità in un sistema di riferimento inerziale) U. Gasparini, Fisica I 4

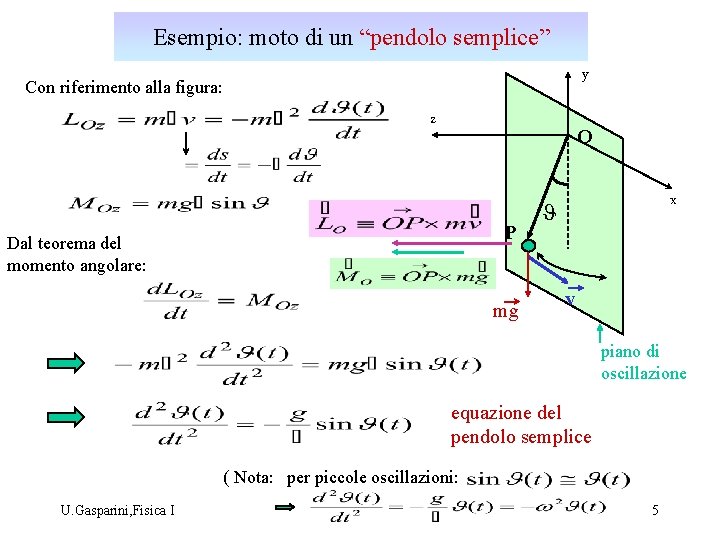
Esempio: moto di un “pendolo semplice” y Con riferimento alla figura: z O P Dal teorema del momento angolare: mg x J v piano di oscillazione equazione del pendolo semplice ( Nota: per piccole oscillazioni: U. Gasparini, Fisica I 5

Teorema del momento dell’impulso Integrando rispetto al tempo l’equazione che esprime il teorema del momento angolare, si ha: In particolare, se il momento è applicato per un tempo sufficientemente breve affinchè il punto di applicazione di F(t) possa essere considerato costante : r (t) = r. O J impulso della forza F “teorema del momento dell’impulso” “momento dell’impulso” U. Gasparini, Fisica I 6

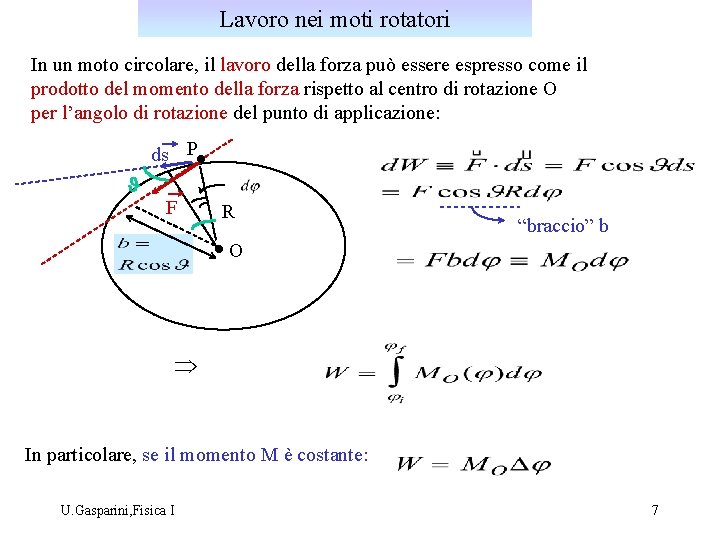
Lavoro nei moti rotatori In un moto circolare, il lavoro della forza può essere espresso come il prodotto del momento della forza rispetto al centro di rotazione O per l’angolo di rotazione del punto di applicazione: ds P J F R “braccio” b O Þ In particolare, se il momento M è costante: U. Gasparini, Fisica I 7

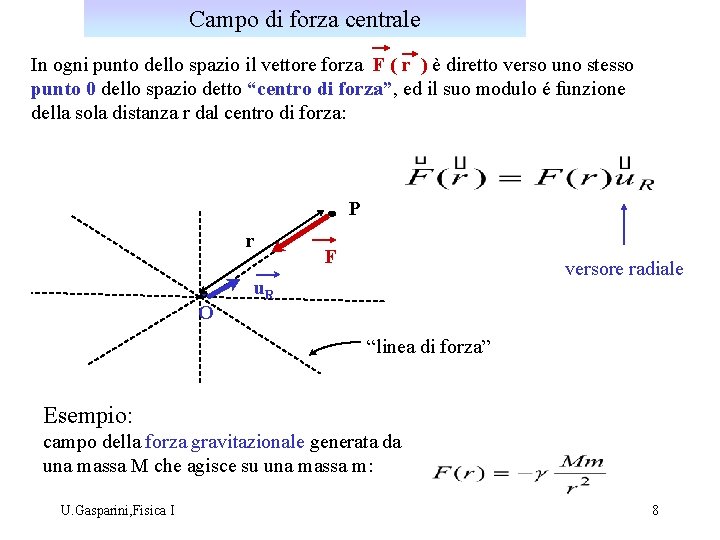
Campo di forza centrale In ogni punto dello spazio il vettore forza F ( r ) è diretto verso uno stesso punto 0 dello spazio detto “centro di forza”, ed il suo modulo é funzione della sola distanza r dal centro di forza: P r O F versore radiale u. R “linea di forza” Esempio: campo della forza gravitazionale generata da una massa M che agisce su una massa m: U. Gasparini, Fisica I 8

Campo di forza centrale (II) un campo di forze centrali è conservativo: il moto avviene conservando l’energia meccanica = dr 1 funzione primitiva di F(r) ds dr il lavoro W 12 non dipende dal cammino percorso u. R 2 O Ad esempio, per un campo di forza gravitazionale: , costante U. Gasparini, Fisica I 9

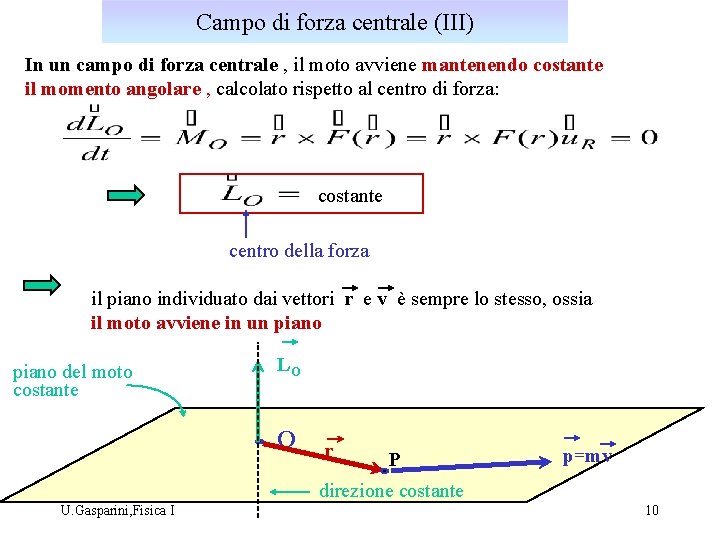
Campo di forza centrale (III) In un campo di forza centrale , il moto avviene mantenendo costante il momento angolare , calcolato rispetto al centro di forza: costante centro della forza il piano individuato dai vettori r e v è sempre lo stesso, ossia il moto avviene in un piano del moto costante LO O r P p=mv direzione costante U. Gasparini, Fisica I 10

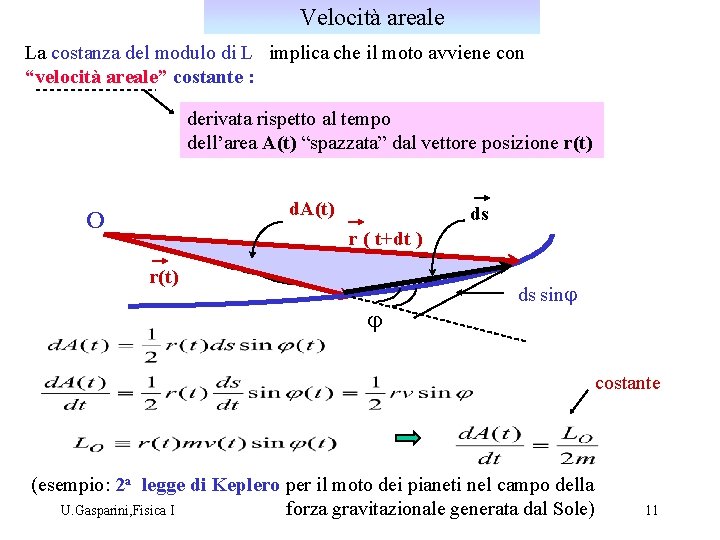
Velocità areale La costanza del modulo di L implica che il moto avviene con “velocità areale” costante : derivata rispetto al tempo dell’area A(t) “spazzata” dal vettore posizione r(t) d. A(t) O ds r ( t+dt ) r(t) j ds sinj costante (esempio: 2 a legge di Keplero per il moto dei pianeti nel campo della forza gravitazionale generata dal Sole) U. Gasparini, Fisica I 11