Moto rotatorio Ripasso ed esempi 1 Un tipico

Moto rotatorio Ripasso ed esempi 1

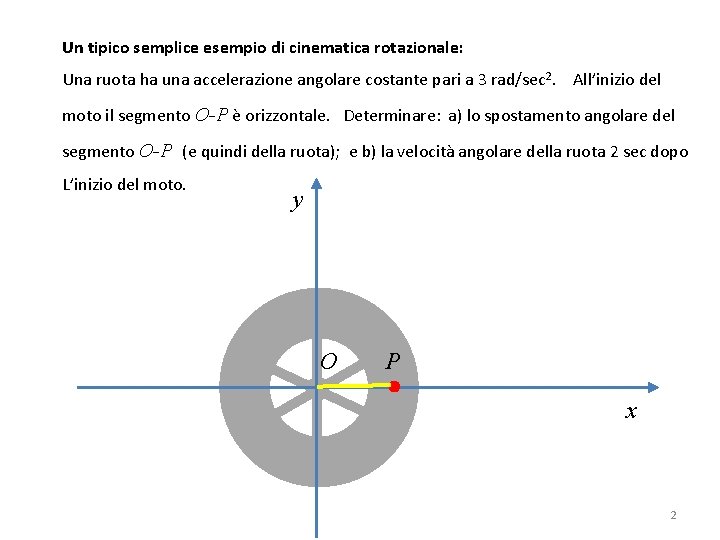
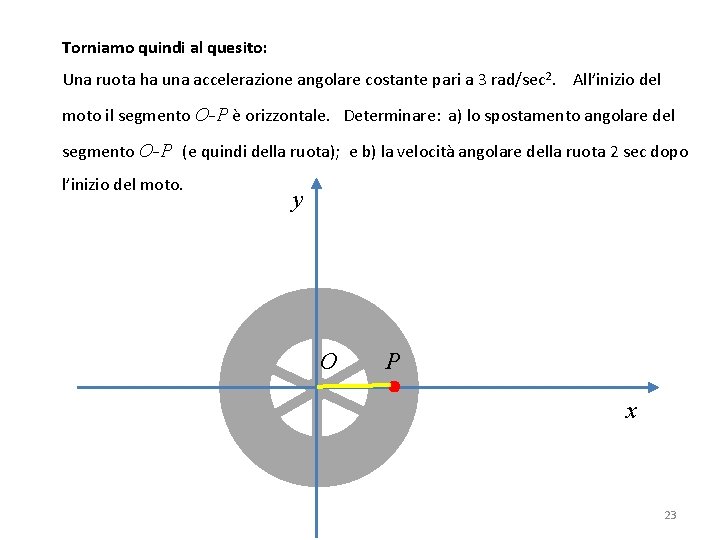
Un tipico semplice esempio di cinematica rotazionale: Una ruota ha una accelerazione angolare costante pari a 3 rad/sec 2. All’inizio del moto il segmento O-P è orizzontale. Determinare: a) lo spostamento angolare del segmento O-P (e quindi della ruota); e b) la velocità angolare della ruota 2 sec dopo L’inizio del moto. y O P x 2

Rivediamo i concetti che abbiamo studiato a riguardo e che ci servono per risolvere il quesito 3

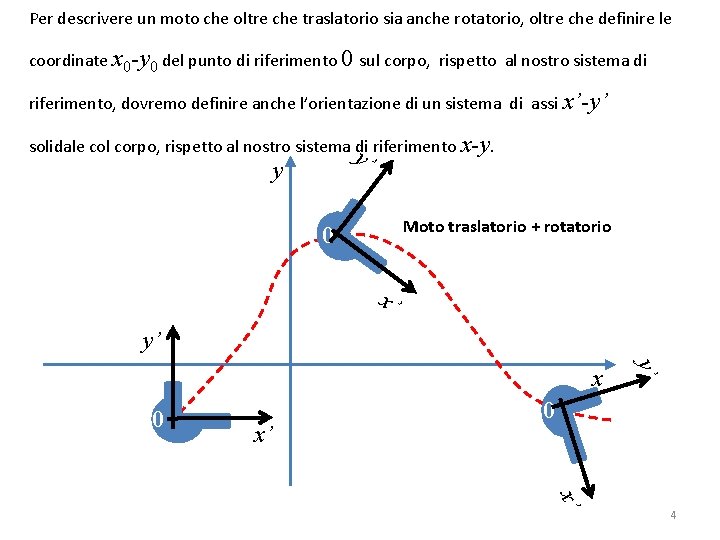
Per descrivere un moto che oltre che traslatorio sia anche rotatorio, oltre che definire le coordinate x 0 -y 0 del punto di riferimento 0 sul corpo, rispetto al nostro sistema di riferimento, dovremo definire anche l’orientazione di un sistema di assi x’-y’ solidale col corpo, rispetto al nostro sistema di riferimento x-y. y ’ y Moto traslatorio + rotatorio 0 x’ y’ x 0 x’ 4

Abbiamo stabilito di studiare questo tipo di moto separando il moto traslatorio dal moto rotatorio. Abbiamo applicato in sostanza il principio di sovrapposizione. Cioè: ad ogni istante lo stato del corpo è definibile in base ad una traslazione + una rotazione 5

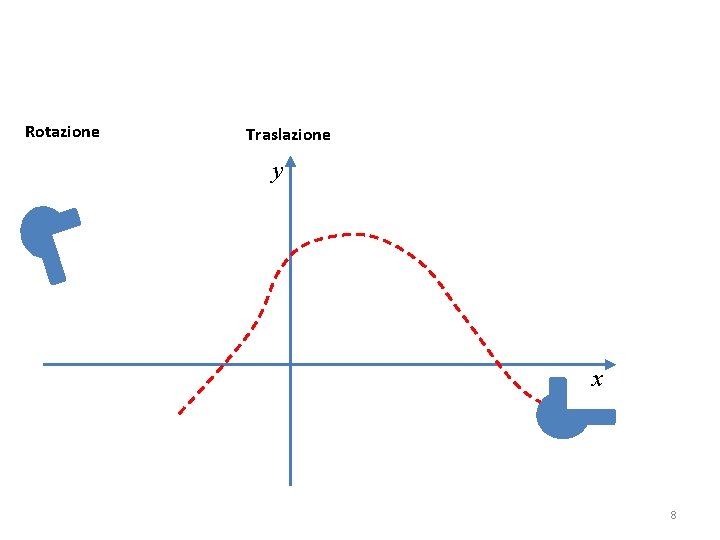
Rotazione Traslazione y x 6

Rotazione Traslazione y x 7

Rotazione Traslazione y x 8

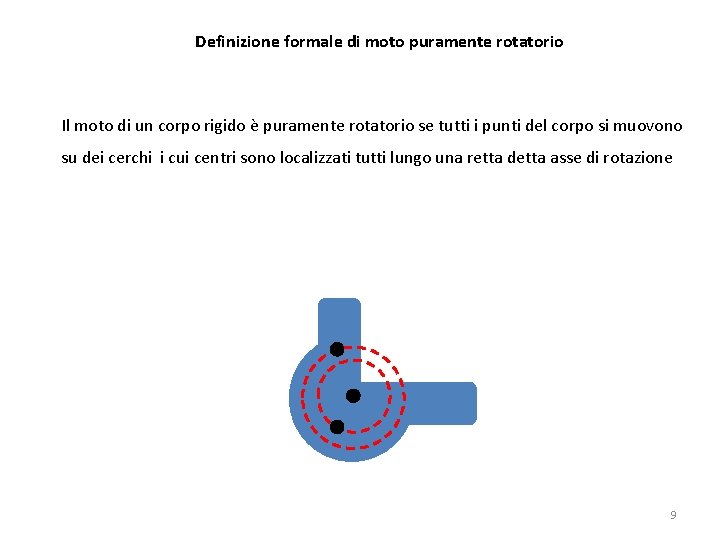
Definizione formale di moto puramente rotatorio Il moto di un corpo rigido è puramente rotatorio se tutti i punti del corpo si muovono su dei cerchi i cui centri sono localizzati tutti lungo una retta detta asse di rotazione 9

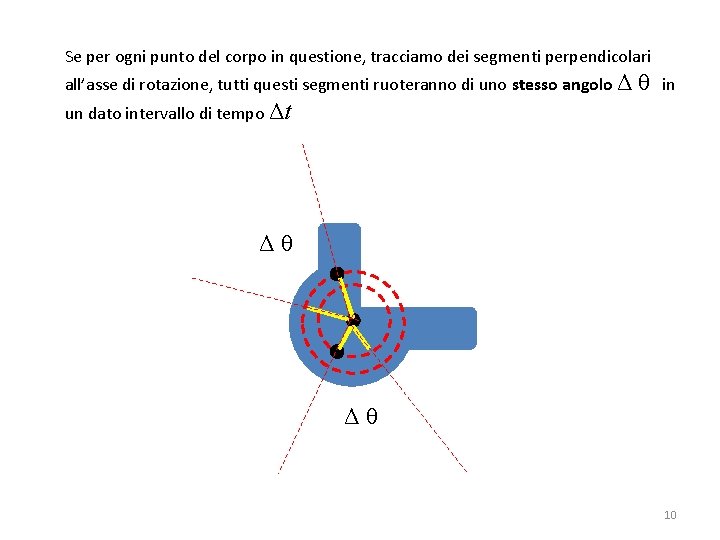
Se per ogni punto del corpo in questione, tracciamo dei segmenti perpendicolari all’asse di rotazione, tutti questi segmenti ruoteranno di uno stesso angolo Δ θ in un dato intervallo di tempo Δt Δθ Δθ 10

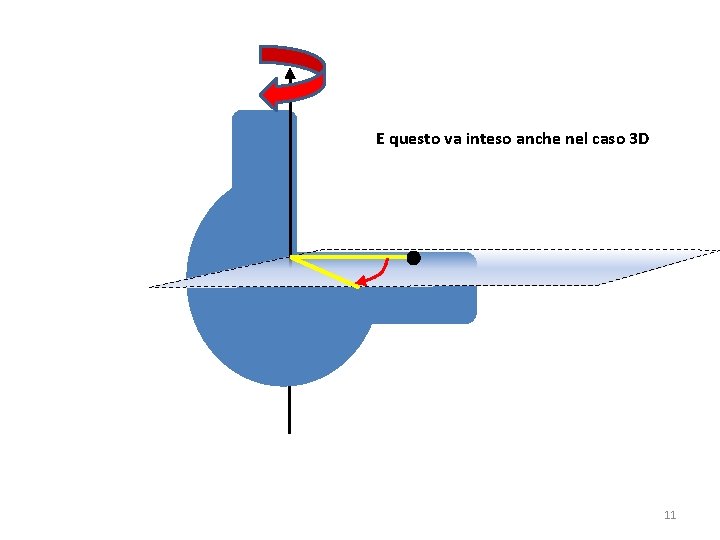
E questo va inteso anche nel caso 3 D 11

E questo va inteso anche nel caso 3 D 12

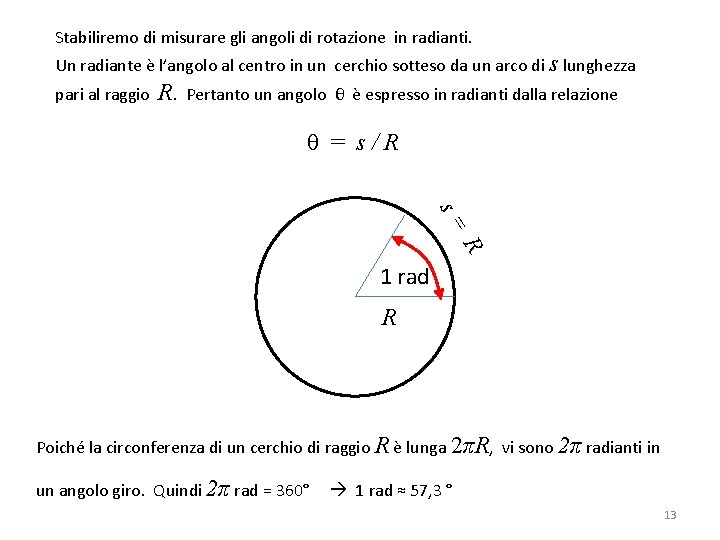
Stabiliremo di misurare gli angoli di rotazione in radianti. Un radiante è l’angolo al centro in un cerchio sotteso da un arco di s lunghezza pari al raggio R. Pertanto un angolo θ è espresso in radianti dalla relazione θ = s/R s= R 1 rad R Poiché la circonferenza di un cerchio di raggio R è lunga 2πR, vi sono 2π radianti in un angolo giro. Quindi 2π rad = 360° 1 rad ≈ 57, 3 ° 13

Lo spostamento angolare nell’intervallo di tempo Δt Definiremo la velocità angolare media = t 2 − t 1 sarà Δθ = θ 2 − θ 1 < ω > del corpo nell’intervallo Δt : < ω > = (θ 2 − θ 1) / (t 2 − t 1 ) = Δθ / Δt In perfetta analogia con quanto abbiamo studiato in cinematica nel caso lineare, la velocità angolare istantanea sarà data dal limite per Δt 0 di questo rapporto: ω(t) = lim Δθ / Δt = dθ /dt Δt 0 In analogia con quanto abbiamo già studiato, indicate con ω1 e agli istanti t 1 e t 2 l’accelerazione angolare media ω2 le velocità angolari < α > è definita dalla relazione: < α > = (ω2 − ω1) / (t 2 − t 1 ) = Δ ω / Δt e di conseguenza l’accelerazione angolare istantanea è data dalla relazione α (t) = lim Δ ω / Δt = d ω /dt Δt 0 14

La velocità angolare ha le dimensioni dell’inverso di un tempo: [ T -1 ] e in generale l’unità di misura è il radiante / sec L’accelerazione angolare ha le dimensioni dell’inverso di un tempo quadrato: [ T -2 ] e in generale l’unità di misura è il radiante / sec 2 15

Analogia fra le grandezze cinematiche lineari e quelle angolari Caso lineare Caso rotazionale x [L] θ [] v = dx /dt [L T-1] ω = dθ /dt [T-1] a = dv/dt = d 2 x/dt 2 [L T-2] α = dω/dt = d 2θ/dt 2 [T-2] Le dimensioni lineari differiscono dalle corrispondenti dimensioni angolari per un fattore avente dimensione di una lunghezza, il che deriva dalla definizione di radiante θ= s / R che è un numero puro, essendo il rapporto fra due lunghezze 16

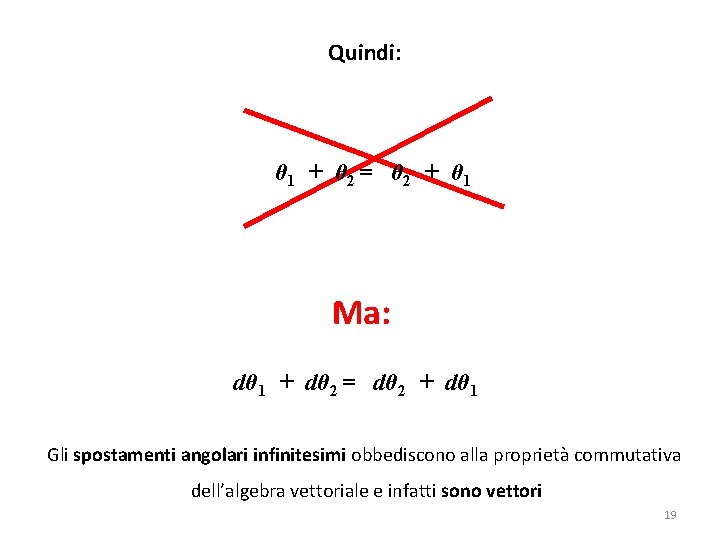
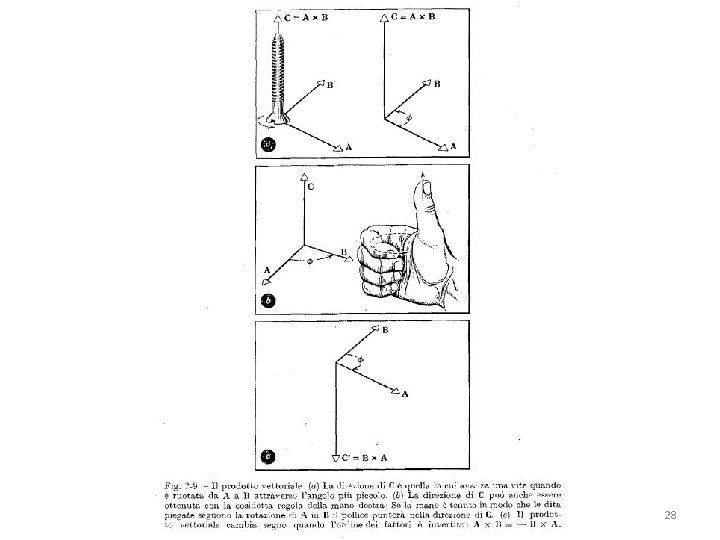
Queste grandezze sono vettori ? Consideriamo il caso dello spostamento angolare θ Si può verificare sperimentalmente che gli spostamenti angolari non si sommano come vettori. Infatti se si sommassero come vettori dovrebbero obbedire alle regole sulla somma dei vettori e in particolare alla proprietà commutativa della somma di due vettori, cioè: θ 1 + θ 2 = θ 2 + θ 1 17

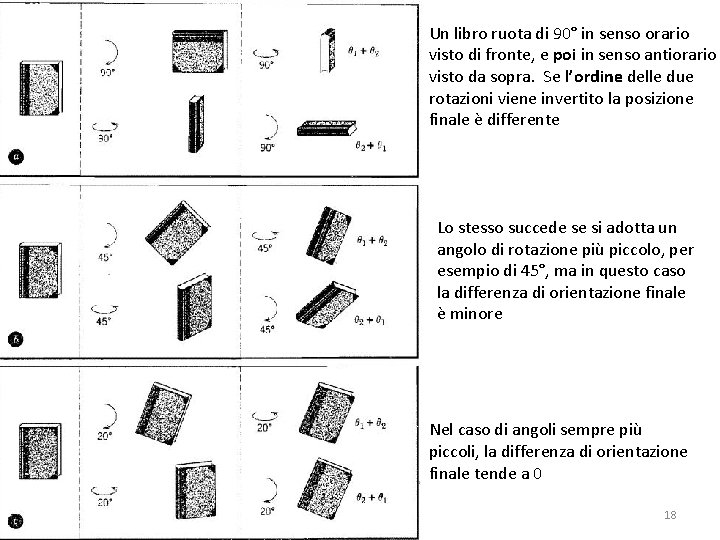
Un libro ruota di 90° in senso orario visto di fronte, e poi in senso antiorario visto da sopra. Se l’ordine delle due rotazioni viene invertito la posizione finale è differente Lo stesso succede se si adotta un angolo di rotazione più piccolo, per esempio di 45°, ma in questo caso la differenza di orientazione finale è minore Nel caso di angoli sempre più piccoli, la differenza di orientazione finale tende a 0 18

Quindi: θ 1 + θ 2 = θ 2 + θ 1 Ma: dθ 1 + dθ 2 = dθ 2 + dθ 1 Gli spostamenti angolari infinitesimi obbediscono alla proprietà commutativa dell’algebra vettoriale e infatti sono vettori 19

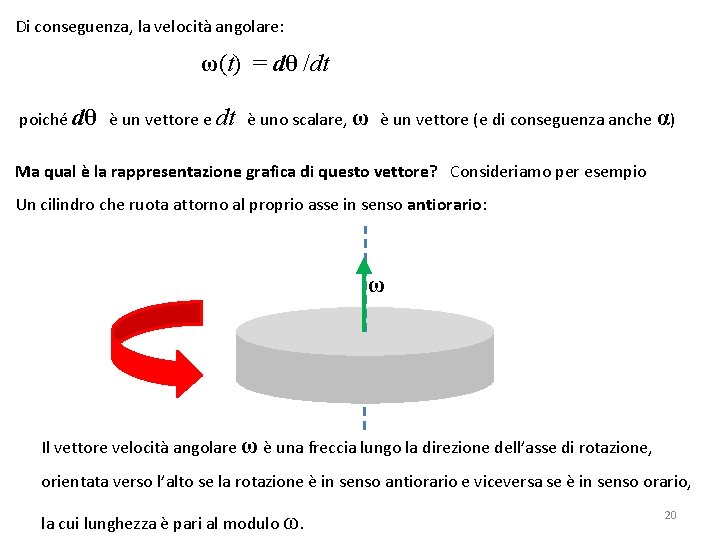
Di conseguenza, la velocità angolare: ω(t) = dθ /dt poiché dθ è un vettore e dt è uno scalare, ω è un vettore (e di conseguenza anche α) Ma qual è la rappresentazione grafica di questo vettore? Consideriamo per esempio Un cilindro che ruota attorno al proprio asse in senso antiorario: ω Il vettore velocità angolare ω è una freccia lungo la direzione dell’asse di rotazione, orientata verso l’alto se la rotazione è in senso antiorario e viceversa se è in senso orario, la cui lunghezza è pari al modulo ω. 20

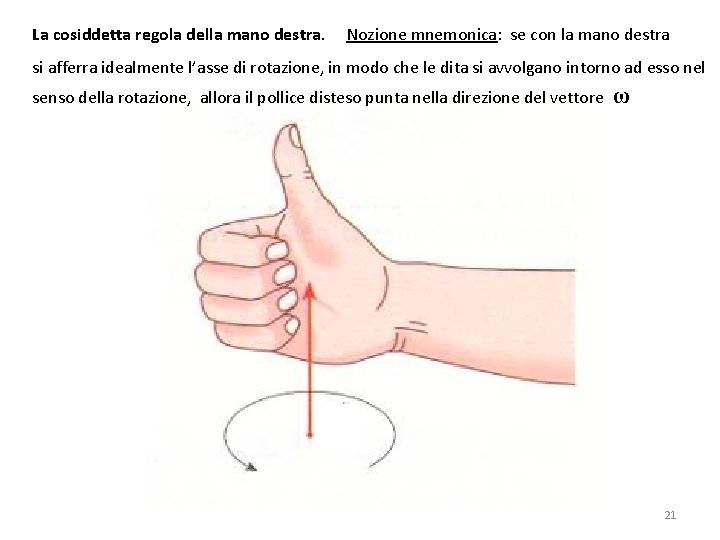
La cosiddetta regola della mano destra. Nozione mnemonica: se con la mano destra si afferra idealmente l’asse di rotazione, in modo che le dita si avvolgano intorno ad esso nel senso della rotazione, allora il pollice disteso punta nella direzione del vettore ω 21

Rotazione con accelerazione angolare costante Il caso più semplice di un moto rotatorio è quello che avviene con accelerazione costante In questo caso le equazioni del moto sono del tutto analoghe a quelle lineari (moto traslatorio): Moto traslatorio Moto rotatorio v = v 0 + a t ω = ω0 + α t x = ½ ( v 0 + v ) t θ = ½ ( ω0 + ω ) t x = v 0 t + ½ a t 2 θ = ω0 t + ½ α t 2 22

Torniamo quindi al quesito: Una ruota ha una accelerazione angolare costante pari a 3 rad/sec 2. All’inizio del moto il segmento O-P è orizzontale. Determinare: a) lo spostamento angolare del segmento O-P (e quindi della ruota); e b) la velocità angolare della ruota 2 sec dopo l’inizio del moto. y O P x 23

(a) L’accelerazione angolare α e il tempo θ All’inizio del moto si ha t =0 ω0 = t sono dati, vogliamo trovare θ. Quindi useremo la = ω0 t + ½ α t 2 0 e α = 3 rad/sec 2 Dopo 2 sec si avrà: θ = 0 x 2 sec + ½ (3 rad/sec 2) (2 sec)2 = 6 rad (b) l’accelerazione α e il tempo t sono dati, vogliamo ottenere ω, quindi useremo la: ω = ω0 + α t e cioè: ω = 0 + (3 rad/sec 2) (2 sec) = 6 rad/sec 24

Se in un esempio del genere interviene una forza ci potrebbe essere chiesto di calcolarne il momento… 25

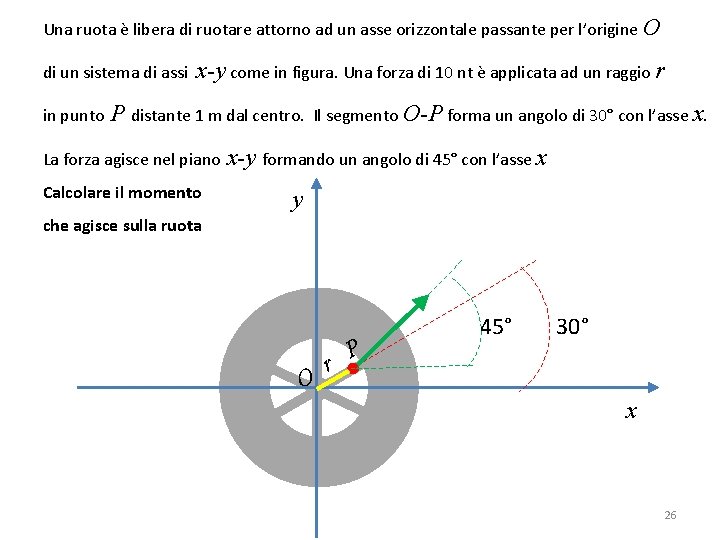
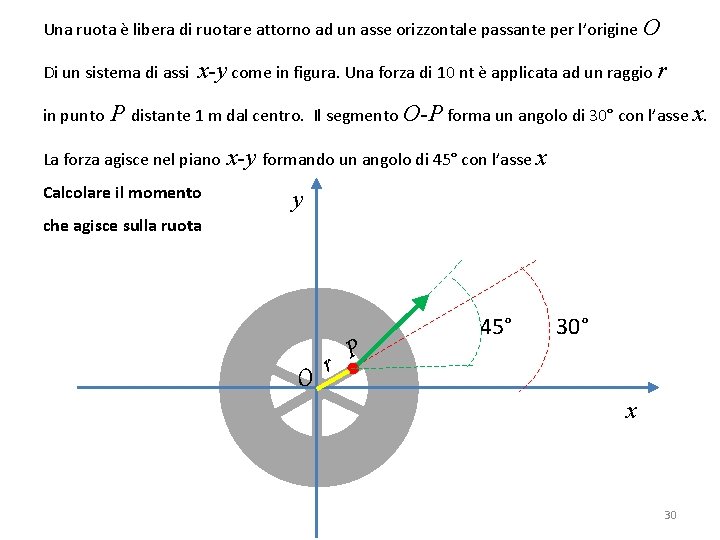
Una ruota è libera di ruotare attorno ad un asse orizzontale passante per l’origine O di un sistema di assi x-y come in figura. Una forza di 10 nt è applicata ad un raggio r in punto P distante 1 m dal centro. Il segmento O-P forma un angolo di 30° con l’asse x. La forza agisce nel piano Calcolare il momento x-y formando un angolo di 45° con l’asse x y che agisce sulla ruota O r P 45° 30° x 26

Momento di una forza Definizione: Se una forza F agisce su un punto P la cui posizione rispetto al riferimento O è individuata da un vettore r, il momento della forza rispetto a O è un vettore definito dalla: τ=rx F dove il simbolo x rappresenta il prodotto vettoriale fra r e F Il modulo di τ è dato dalla relazione: τ = r F sin θ dove θ è l’angolo fra r e F La direzione è ortogonale al piano individuato da la regola della mano destra r e F, e il verso segue 27

28

Le dimensioni del momento della forza sono quelle di forza x distanza E cioè [ M L T− 2 L ] [ M L 2 T− 2 ] L’unità di misura il nt-metro Vediamo adesso di risolvere il quesito che ci era stato proposto 29

Una ruota è libera di ruotare attorno ad un asse orizzontale passante per l’origine O Di un sistema di assi x-y come in figura. Una forza di 10 nt è applicata ad un raggio r in punto P distante 1 m dal centro. Il segmento O-P forma un angolo di 30° con l’asse x. La forza agisce nel piano Calcolare il momento x-y formando un angolo di 45° con l’asse x y che agisce sulla ruota O r P 45° 30° x 30

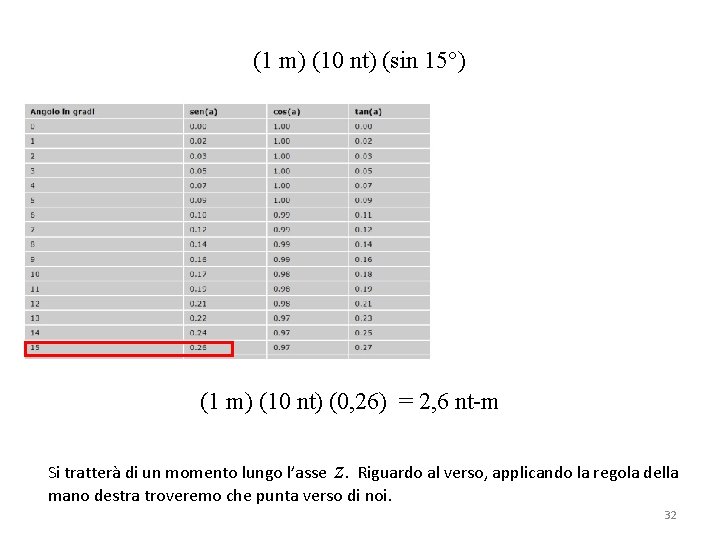
Applichiamo la definizione di momento di una forza: τ=rx F dove il simbolo x rappresenta il prodotto vettoriale fra r e F Il modulo di τ è dato dalla relazione: τ = r F sin θ In questo caso l’angolo θ è dato da: θ = 45° − 30° = 15° Pertanto il modulo del momento è dato da: τ = r F sin θ = (1 m) (10 nt) (sin 15°) 31

(1 m) (10 nt) (sin 15°) (1 m) (10 nt) (0, 26) = 2, 6 nt-m Si tratterà di un momento lungo l’asse z. Riguardo al verso, applicando la regola della mano destra troveremo che punta verso di noi. 32

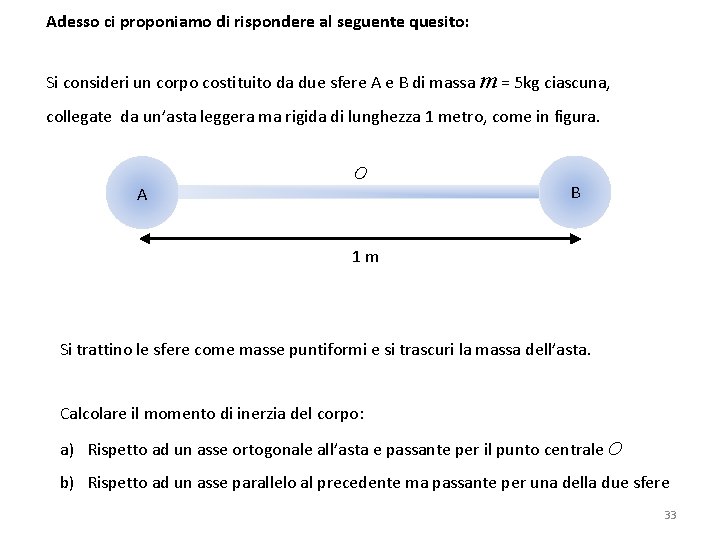
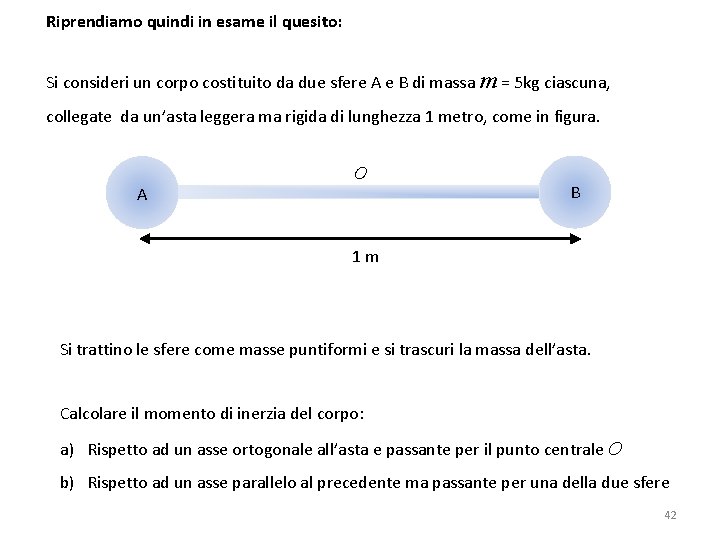
Adesso ci proponiamo di rispondere al seguente quesito: Si consideri un corpo costituito da due sfere A e B di massa m = 5 kg ciascuna, collegate da un’asta leggera ma rigida di lunghezza 1 metro, come in figura. A O B 1 m Si trattino le sfere come masse puntiformi e si trascuri la massa dell’asta. Calcolare il momento di inerzia del corpo: a) Rispetto ad un asse ortogonale all’asta e passante per il punto centrale O b) Rispetto ad un asse parallelo al precedente ma passante per una della due sfere 33

Avevamo visto che il concetto di momento di inerzia era stato introdotto a proposito della formulazione dell’energia cinetica di rotazione. Rivediamo 34

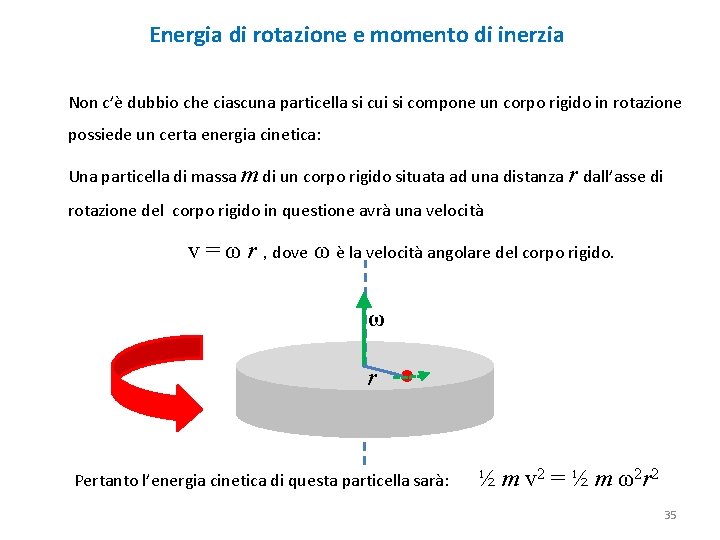
Energia di rotazione e momento di inerzia Non c’è dubbio che ciascuna particella si cui si compone un corpo rigido in rotazione possiede un certa energia cinetica: Una particella di massa m di un corpo rigido situata ad una distanza r dall’asse di rotazione del corpo rigido in questione avrà una velocità v = ω r , dove ω è la velocità angolare del corpo rigido. ω r Pertanto l’energia cinetica di questa particella sarà: ½ m v 2 = ½ m ω2 r 2 35

Se, come stiamo supponendo, il corpo è rigido allora la velocità angolare ω è la stessa per tutte le particelle di cui si compone, e l’energia cinetica totale K sarà la somma delle energie cinetiche di tutte le particelle : K = ½ m 1 ω2 r 21 + ½ m 2 r 22 + …………. . ½ m. N ω2 r 2 N K = ½ ( m 1 r 21 + m 2 r 22 + …………. . m. N r 2 N ) ω2 K = ½ ∑(m r Il termine ∑(m r i i 2 i ) ω2 2 i ) che indichiamo col simbolo I è denominato Momento di Inerzia del corpo rigido rispetto a quel particolare asse di rotazione I = ∑(m r i 2 i ) 36

Va sottolineato che il Momento di Inerzia di un corpo rigido dipende quindi dall’asse, oltre che dalla forma del corpo e dalla distribuzione delle masse. Il Momento di Inerzia I ha dimensioni: [ M L 2 ] e si misura in: kg m 2 Introducendo il Momento di Inerzia, l’energia cinetica di un corpo rigido in rotazione Krot è espressa pertanto dalla: Krot = ½ I ω2 37

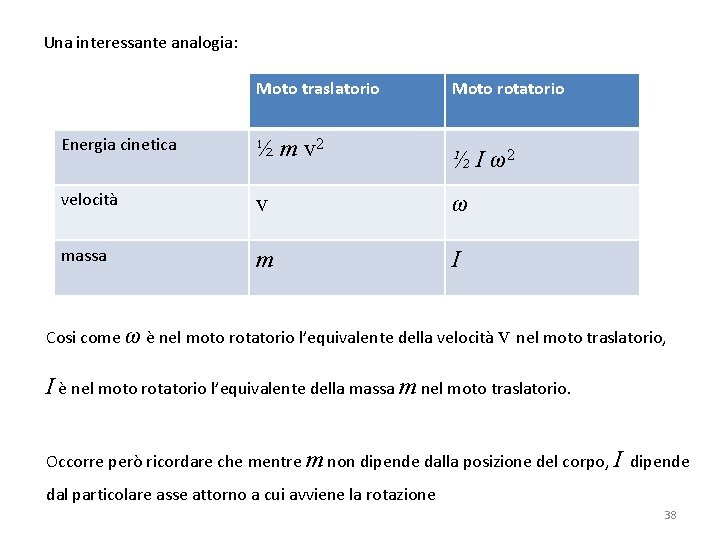
Una interessante analogia: Moto traslatorio Moto rotatorio Energia cinetica ½ m v 2 ½ I ω2 velocità v ω massa m I Cosi come ω è nel moto rotatorio l’equivalente della velocità v nel moto traslatorio, I è nel moto rotatorio l’equivalente della massa m nel moto traslatorio. Occorre però ricordare che mentre m non dipende dalla posizione del corpo, I dipende dal particolare asse attorno a cui avviene la rotazione 38

Nel caso in cui il corpo rigido non è costituito da un insieme finito di particelle distinte, ma è costituito da una distribuzione continua di materia, l’operazione di somma che compare nella formula: I = ∑(m r 2 i i ) diventerà una integrazione: considereremo il corpo costituito da masse infinitesime dm e considereremo la distanza r fra tali masse e l’asse di rotazione: I = ∫ r 2 dm dove l’integrale è esteso sull’intero corpo 39

Nel caso di corpi di forma complicata, il calcolo di questo integrale può essere difficile, ma nel caso di corpi con una geometria regolare e l’asse di rotazione coincidente con l’asse di simmetria, il calcolo è abbastanza semplice. Ecco di seguito alcuni esempi: 40

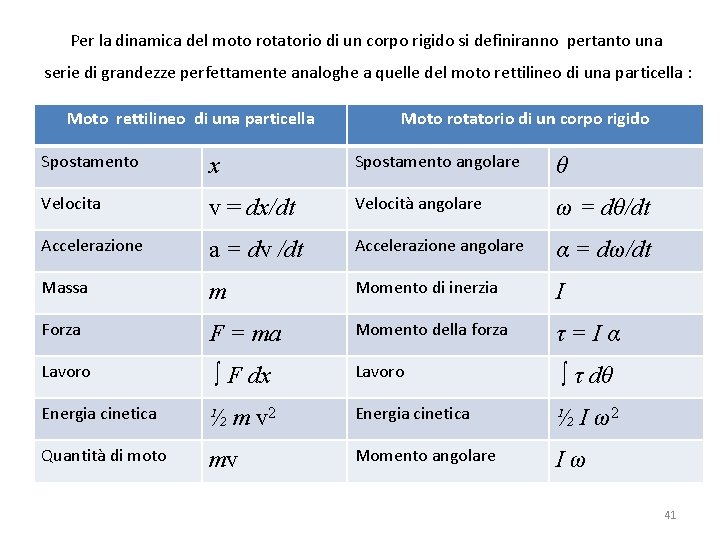
Per la dinamica del moto rotatorio di un corpo rigido si definiranno pertanto una serie di grandezze perfettamente analoghe a quelle del moto rettilineo di una particella : Moto rettilineo di una particella Moto rotatorio di un corpo rigido Spostamento x Spostamento angolare θ Velocita v = dx/dt Velocità angolare ω = dθ/dt Accelerazione a = dv /dt Accelerazione angolare α = dω/dt Massa m Momento di inerzia I Forza F = ma Momento della forza τ=Iα Lavoro ∫ F dx Lavoro ∫ τ dθ Energia cinetica ½ m v 2 Energia cinetica ½ I ω2 Quantità di moto mv Momento angolare Iω 41

Riprendiamo quindi in esame il quesito: Si consideri un corpo costituito da due sfere A e B di massa m = 5 kg ciascuna, collegate da un’asta leggera ma rigida di lunghezza 1 metro, come in figura. A O B 1 m Si trattino le sfere come masse puntiformi e si trascuri la massa dell’asta. Calcolare il momento di inerzia del corpo: a) Rispetto ad un asse ortogonale all’asta e passante per il punto centrale O b) Rispetto ad un asse parallelo al precedente ma passante per una della due sfere 42

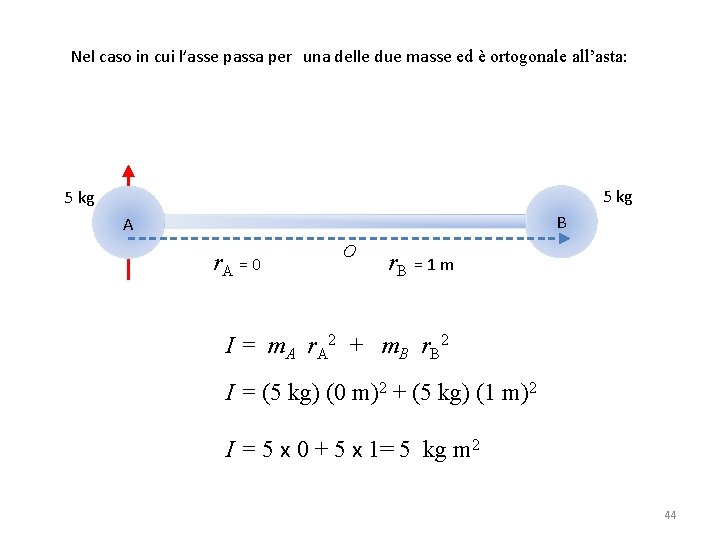
Riscriviamo la formula per il momento di inerzia nel caso di masse puntiformi: I = ∑(m r i 2 i ) Nel caso in cui l’asse passa per O ed è ortogonale all’asta: 5 kg B A r. A = − 0. 5 m O r. B = 0. 5 m I = m A r A 2 + m B r B 2 I = (5 kg) (0. 5 m)2 + (5 kg) (0. 5 m)2 I = 5 x 0. 25 + 5 x 0. 25 = 2. 5 kg m 2 43

Nel caso in cui l’asse passa per una delle due masse ed è ortogonale all’asta: 5 kg B A r. A = 0 O r. B = 1 m I = m A r A 2 + m B r B 2 I = (5 kg) (0 m)2 + (5 kg) (1 m)2 I = 5 x 0 + 5 x 1= 5 kg m 2 44

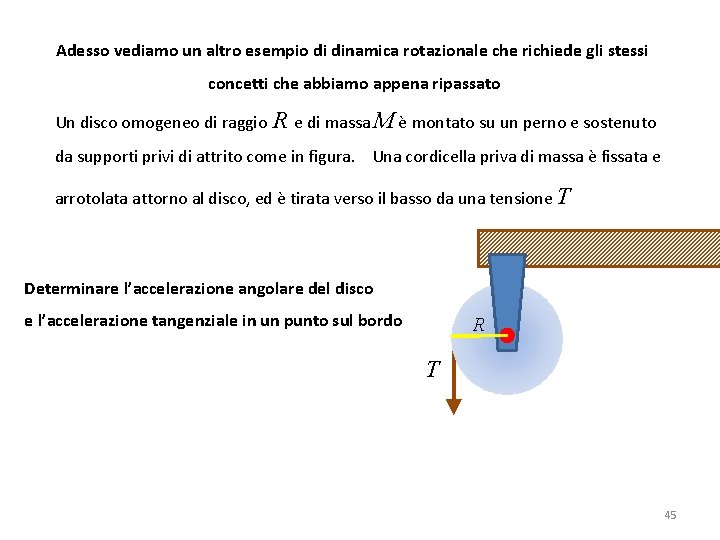
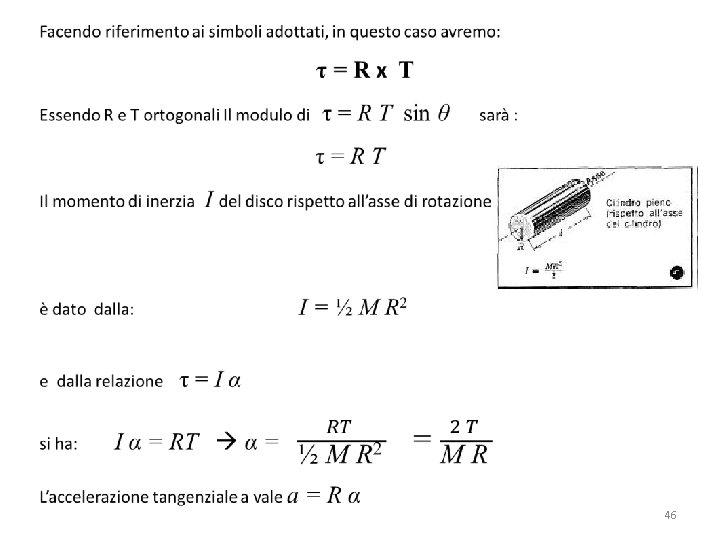
Adesso vediamo un altro esempio di dinamica rotazionale che richiede gli stessi concetti che abbiamo appena ripassato Un disco omogeneo di raggio R e di massa M è montato su un perno e sostenuto da supporti privi di attrito come in figura. Una cordicella priva di massa è fissata e arrotolata attorno al disco, ed è tirata verso il basso da una tensione T Determinare l’accelerazione angolare del disco e l’accelerazione tangenziale in un punto sul bordo R T 45

46

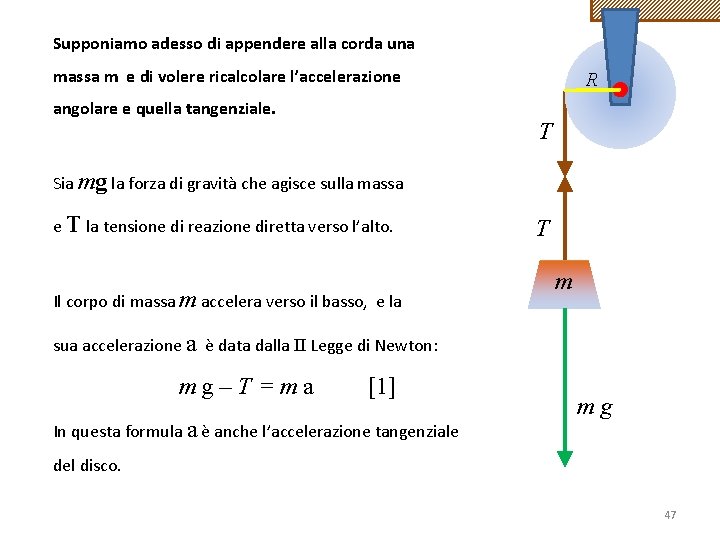
Supponiamo adesso di appendere alla corda una massa m e di volere ricalcolare l’accelerazione angolare e quella tangenziale. R T Sia mg la forza di gravità che agisce sulla massa e T la tensione di reazione diretta verso l’alto. Il corpo di massa m accelera verso il basso, e la T m sua accelerazione a è data dalla II Legge di Newton: mg–T=ma [1] In questa formula a è anche l’accelerazione tangenziale mg del disco. 47

Per l’accelerazione angolare α potremo scrivere di nuovo: τ = Iα RT = ½ M R 2 α T = ½ M Rα e ricordando che R α T =a si ha: =½Ma Riscrivendo la [1]: m g – T = m a avremo le due equazioni: mg–T=ma T =½Ma Con due equazioni e due incognite (T e a), possiamo risolvere il quesito. 48

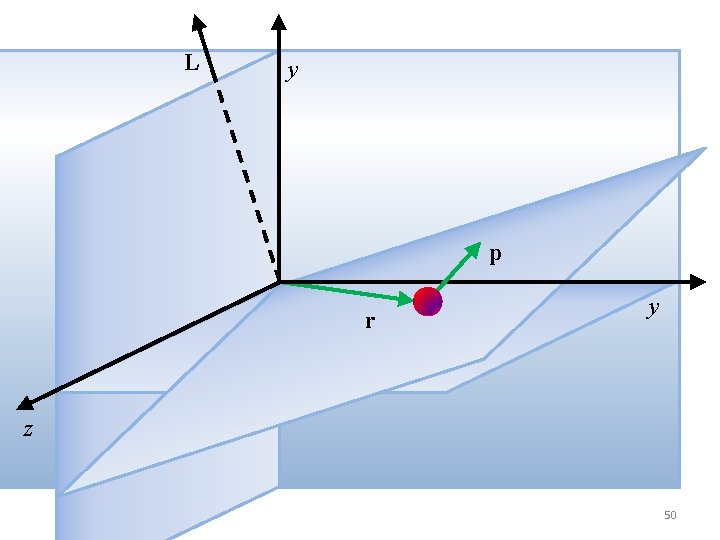
Momento angolare di una particella Nella dinamica del moto rotatorio, il concetto di momento angolare (o momento della quantità di moto) ha un ruolo simile a quello che ha la quantità di moto nella dinamica del moto traslatorio. Vedremo che la definizione e l’applicazione di questo concetto ci permetterà di ricavare un’altra importante Legge di conservazione. Consideriamo una particella di massa m e quantità di moto p situata ad una distanza r dall’origine O di un sistema di assi x-y-z. Il momento angolare della particella rispetto al punto O è definito dalla: L = rxp Cioè: il prodotto vettoriale di r per p 49

L y p r y z 50

In accordo con la definizione di prodotto vettoriale, il modulo di L è dato da: L = r p sin θ La direzione è perpendicolare al piano individuato dai due vettori r e p Il verso è stabilito dalla consueta regola della mano destra. Dalla definizione, che è del tutto analoga al momento di una forza, si vede che il momento angolare L è il momento della quantità di moto. 51

Cioè: la derivata rispetto al tempo del momento angolare (o momento della quantità di moto) di particella è uguale al momento delle forze applicate alla particella stessa. 52

54

55

Conservazione del momento angolare 56

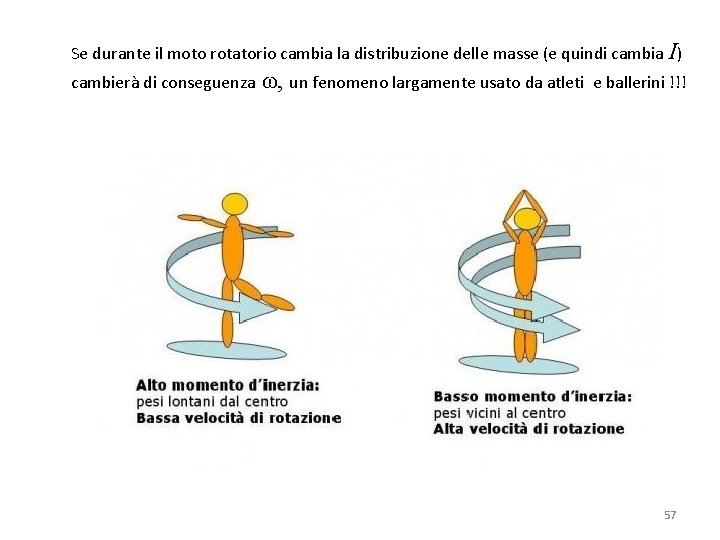
Se durante il moto rotatorio cambia la distribuzione delle masse (e quindi cambia I) cambierà di conseguenza ω, un fenomeno largamente usato da atleti e ballerini !!! 57

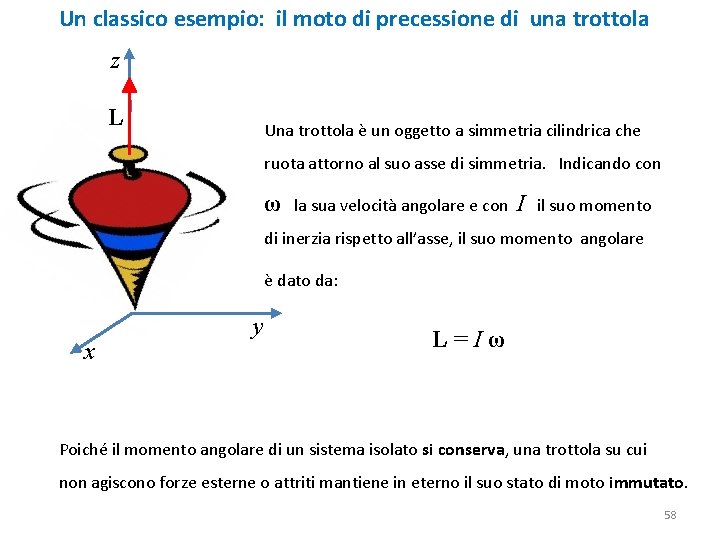
Un classico esempio: il moto di precessione di una trottola z L Una trottola è un oggetto a simmetria cilindrica che ruota attorno al suo asse di simmetria. Indicando con ω la sua velocità angolare e con I il suo momento di inerzia rispetto all’asse, il suo momento angolare è dato da: x y L=Iω Poiché il momento angolare di un sistema isolato si conserva, una trottola su cui non agiscono forze esterne o attriti mantiene in eterno il suo stato di moto immutato. 58

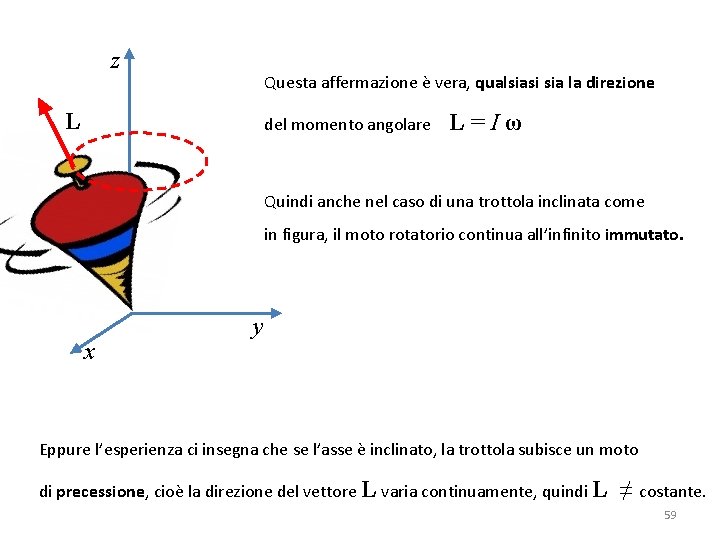
z Questa affermazione è vera, qualsiasi sia la direzione L del momento angolare L=Iω Quindi anche nel caso di una trottola inclinata come in figura, il moto rotatorio continua all’infinito immutato. x y Eppure l’esperienza ci insegna che se l’asse è inclinato, la trottola subisce un moto di precessione, cioè la direzione del vettore L varia continuamente, quindi L ≠ costante. 59

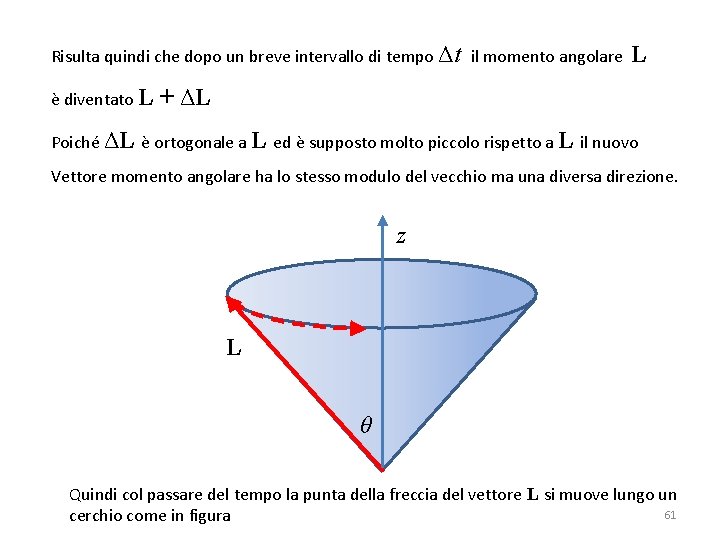
Come spieghiamo questo fenomeno ? Evidentemente nel caso reale la trottola non è un sistema isolato: su di essa agisce la forza di gravitazione. Vediamo allora di capire cosa succede. Sia m la massa della trottola, sia θ l’angolo dell’asse della trottola rispetto alla verticale, e consideriamo il momento τ rispetto al punto di appoggio O esercitato dalla forza di gravità mg sul baricentro della trottola, individuato da un vettore L z r come in figura. =rx mg il cui modulo è: τ = r m g sin θ Scriveremo: τ θ La direzione di τ è ortogonale al piano individuato da r e g Questa stessa sarà quindi la direzione della variazione di momento r angolare ΔL in un breve tempo Δt mg x O y , in quanto risulta: ΔL = τ Δt 60

Risulta quindi che dopo un breve intervallo di tempo Δt il momento angolare L è diventato L + ΔL Poiché ΔL è ortogonale a L ed è supposto molto piccolo rispetto a L il nuovo Vettore momento angolare ha lo stesso modulo del vecchio ma una diversa direzione. z L θ Quindi col passare del tempo la punta della freccia del vettore L si muove lungo un 61 cerchio come in figura

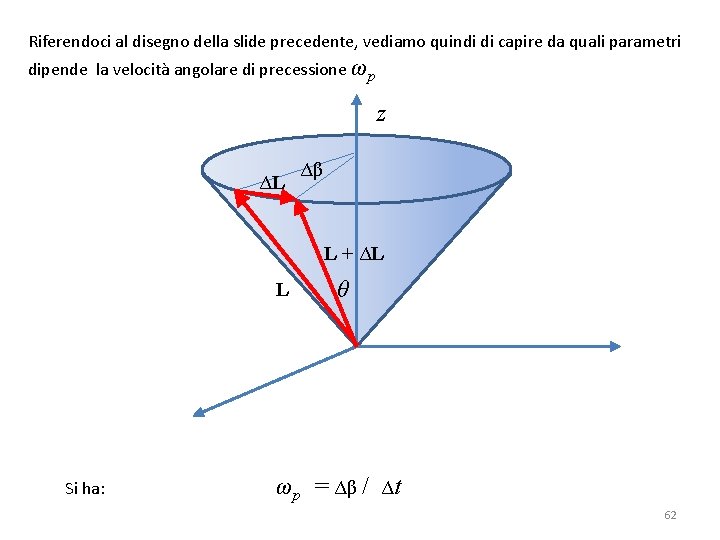
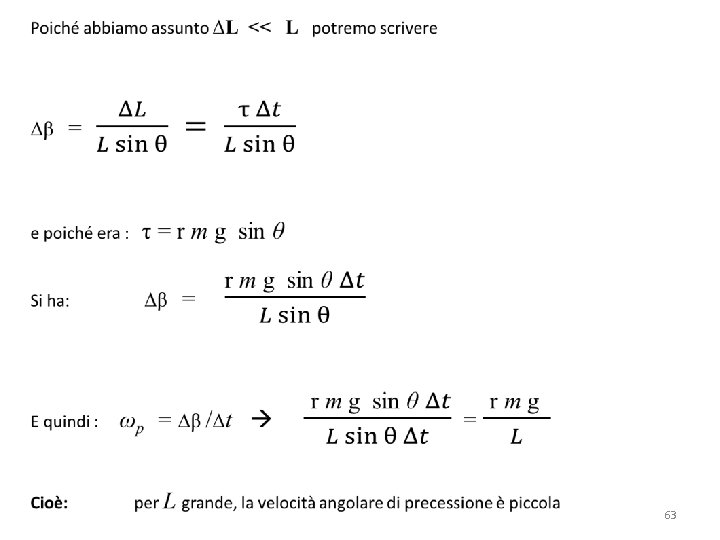
Riferendoci al disegno della slide precedente, vediamo quindi di capire da quali parametri dipende la velocità angolare di precessione ωp z ΔL Δβ L + ΔL L Si ha: ωp θ = Δβ / Δt 62

63