Matematica Generale A cura di Beatrice Venturi Derivate

Matematica Generale A cura di Beatrice Venturi Derivate 23 -feb-21 1

1. INTRODUZIONE AL CONCETTO DI DERIVATA Problema: determinare la tangente in un generico punto ad una curva data. Tale problema venne risolto dai greci in modo elementare nel caso della circonferenza. 23 -feb-21 2

Circonferenza e retta tangente 23 -feb-21 3

1. INTRODUZIONE AL CONCETTO DI DERIVATA Per determinare la tangente in un punto abbiamo bisogno di conoscere la sua inclinazione, cioè il suo coefficiente angolare. Dati due punti: 23 -feb-21 4

INTRODUZIONE AL CONCETTO DI DERIVATA Consideriamo variazione delle ascisse variazione delle ordinate 23 -feb-21 5

INTRODUZIONE AL CONCETTO DI DERIVATA Inclinazione o coefficiente angolare di una retta ( è la tangente trigonometrica all’angolo ) Tasso o saggio di accrescimento della variabile y rispetto alla variabile x 23 -feb-21 6

Definizione di derivata 23 -feb-21 7

Definizione di funzione derivabile Data una funzione f(x) definita in un intervallo I=(a, b) si dice che è derivabile in I se esiste ed è finito il limite del rapporto incrementale x I. 23 -feb-21 8

Retta tangente Data una funzione f(x) definita in un intervallo I=(a, b), l’equazione della retta tangente alla curva f(x) nel punto di ascissa x 0 è: y=f(x 0)+f’(x 0)(x- x 0) 23 -feb-21 9

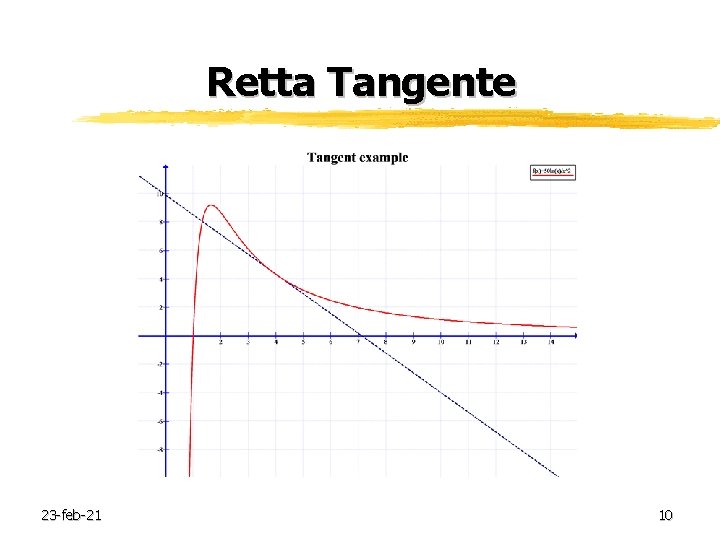
Retta Tangente 23 -feb-21 10

Definizione della derivata prima In tutti i punti in cui fa f(x) è derivabile risulta definita una nuove funzione che si indica con f’(x) oppure con D 1 f(x). La funzione f’(x) assume i valori della derivata della funzione f(x) calcolata per lo stesso valore della x. f’(x) si chiama derivata prima della funzione f(x). 23 -feb-21 11

Definizione della derivata seconda Si chiama derivata seconda della funzione f(x) la derivata prima della funzione f’(x). In tutti i punti in cui fa f(x) è derivabile due volte risulta definita la derivata seconda che si indica con f’’(x) oppure con D 2 f(x). 23 -feb-21 12

Relazione tra derivabilità e continuità Una funzione f(x) derivabile in un punto x è anche continua nello stesso punto. derivabilità continuità Se una funzione f(x) è continua in un punto x NON è detto che sia anche derivabile. 23 -feb-21 13

Relazione tra derivabilità e continuità Contro esempio: y=|x| valutato nell’origine. 23 -feb-21 14

Punto angoloso 23 -feb-21 15

Punto angoloso Data una funzione f(x) definita in un intervallo I = (a, b), sia x I 23 -feb-21 16

Punto con tangente verticale o flesso verticale 23 -feb-21 17

Punto con tangente verticale o flesso verticale Data una funzione f(x) definita in un intervallo I = (a, b), sia x I 23 -feb-21 18

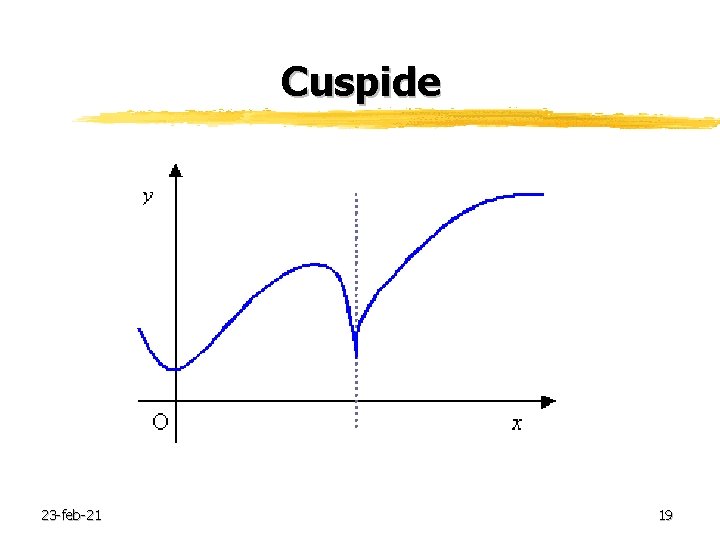
Cuspide 23 -feb-21 19

Cuspide Data una funzione f(x) definita in un intervallo I = (a, b), sia x I 23 -feb-21 20

Regole di derivazione Se f(x) e g(x) sono derivabili in (a, b) allora valgono le seguenti regole: 23 -feb-21 21

Regole di derivazione Addizione e sottrazione: 23 -feb-21 22

Regole di derivazione Prodotto: 23 -feb-21 23

Regole di derivazione Rapporto : nei punti in cui g(x) 0 23 -feb-21 24

Regole di derivazione Logaritmo : 23 -feb-21 25

Regole di derivazione Esponenziale: 23 -feb-21 26

Regole di derivazione Potenza (1) : 23 -feb-21 27

Regole di derivazione Potenza (2): 23 -feb-21 28

Regole di derivazione Prodotto per una costante: 23 -feb-21 29

Regole di derivazione Funzione inversa: Se y=f(x) è una funzione crescente (decrescente) e derivabile nell’intervallo (a, b) allora è dotata di inversa e, in tutti i punti in cui è f’(x) 0, anche la sua funzione inversa f -1(y) è derivabile e si ha: 23 -feb-21 30

Regole di derivazione Funzione composta: Una funzione y=f[g(x)] composta per mezzo di due funzioni derivabili è anch’essa derivabile e si ha che la sua derivata è data da: 23 -feb-21 31

Derivate notevoli Funzione potenza: x R e n N 23 -feb-21 32

Derivate notevoli Funzione esponenziale: x R e a>0 23 -feb-21 33

Derivate notevoli Funzione logaritmica: x>0 e a>0 23 -feb-21 34

Derivate notevoli Funzione radice: x 0 e n N 23 -feb-21 35

Derivate notevoli Funzione iperbole: x R {0} 23 -feb-21 36