Ideal Models in Symmetric Cryptography Stefano Tessaro UC

Ideal Models in Symmetric Cryptography Stefano Tessaro UC Santa Barbara Visions of Cryptography Weizmann Institute

Crypto-History 2000 BC [oversimplified] Cryptographic algorithms designed from scratch, no proofs, … 1982 Provable security: Security of cryptosystems formalized and proven under computational assumptions. Amazingly successful

The Sky is the Limit! Encryption, signatures, multi-party computation, secure delegation, functional encryption, FHE, …

This Talk – In a Nutshell This talk: Biased selection of problems which cannot be studied within the traditional framework of provable security. Leitmotif: Security proofs are in ideal models (e. g. random oracle model, ideal cipher model, etc. ) Two high-level goals: 1 2 Survey a set problems not as widely considered by the core theory community. Thought-provoking: Foster discussion on ideal models, and show why “we are stuck with them”.

Ideal Models Random-oracle model [Fia. Sha 86, Bel. Rog 93] Cryptographic primitives – Set P of valid “instances” Generic-group model § Functions {0, 1}* → {0, 1}n [Sho 97] § Permutations {0, 1}n → {0, 1}n § Pairs (f, op), where f: Zq → {0, 1}n, op(f(a), f(b)) = f(a + b) Ideal-P model: 1. Pick P u. a. r from P 2. Every algorithm (i. e. , attacker, schemes) given access to P. P C Rationale: Ideal primitive P has all security properties expected from P-candidates.

Ideal Models Fact. [Ca. Go. Ha 98] Security proofs in ideal models are not “sound”. This talk. Problems motivated by design of efficient and highlysecure constructions of symmetric cryptographic primitives (block ciphers, hash functions). Ideal models used in security proofs: § § They are only way to give “provable” answers. Security against limited attacker class (i. e. , generic attacks) is partially justified by existing cryptanalytic attacks. “A proof in an ideal model is better than no proof at all. ”

Outline Three selected examples: 1 From Weak to Strong Block Ciphers 2 Hash Functions and Key Derivation 3 Building Ideal Primitives

Pseudorandom Functions [Go. Mi 84] Keyed function F: K × X → Y Q adaptive queries Random function R: X → Y SK R F F(SK, x) x x D D 0/1 R(x) = $ Time T 0/1 Definition. F (T, Q, e)-PRF: ∀(T, Q)-distinguishers D: Pr[D → 1|left] – Pr[D → 1|right] < e [Typically: e = negl for T, Q = poly(k) - here we care about concrete security] PRFs �efficient symmetric encryption, MACs, …

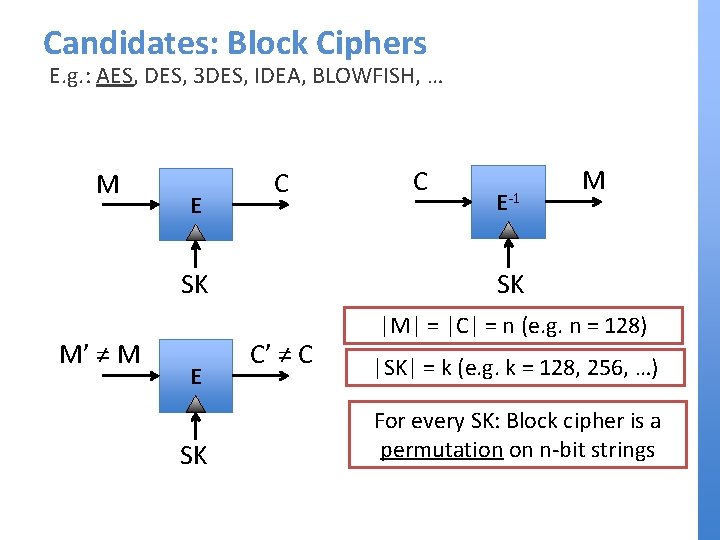
Candidates: Block Ciphers E. g. : AES, DES, 3 DES, IDEA, BLOWFISH, … M E C SK M’ ≠ M E SK C E-1 M SK C’ ≠ C |M| = |C| = n (e. g. n = 128) |SK| = k (e. g. k = 128, 256, …) For every SK: Block cipher is a permutation on n-bit strings

Pseudorandom Permutations [Lub. Rac 85] Block cipher E: K × X → X Random permutation P: X → X SK P E E-1(SK, y) E(SK, x) (-, y) x (+, x) -1(y) P P(x) (-, y) (+, x) x D D 0/1 Definition. E (T, Q, e)-PRP: ∀(T, Q)-distinguishers D: Pr[D → 1|left] – Pr[D → 1|right] < e. STRONG-PRP 0/1

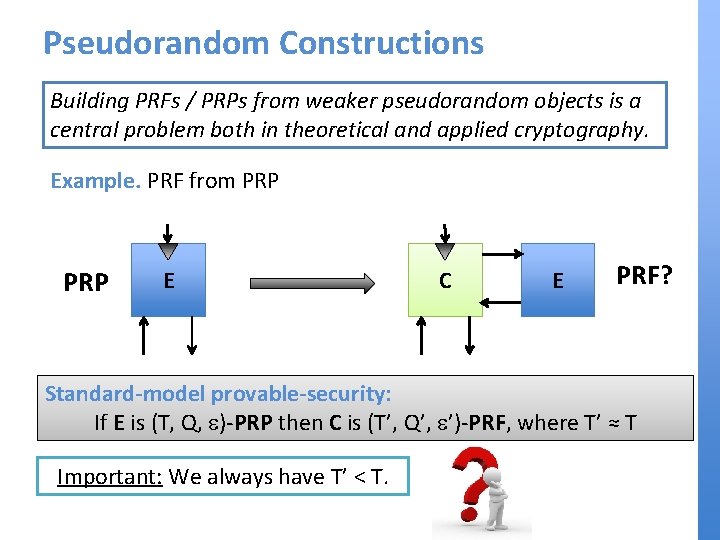
Pseudorandom Constructions Building PRFs / PRPs from weaker pseudorandom objects is a central problem both in theoretical and applied cryptography. Example. PRF from PRP E C E PRF? Standard-model provable-security: If E is (T, Q, e)-PRP then C is (T’, Q’, e’)-PRF, where T’ ≈ T Important: We always have T’ < T.

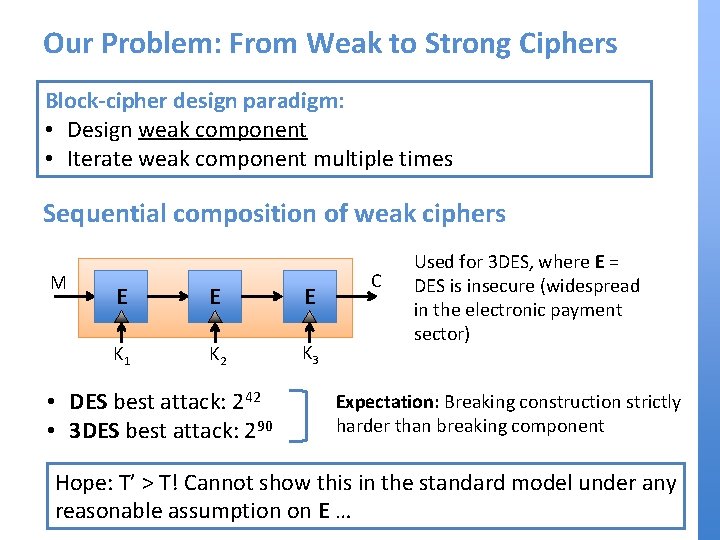
Our Problem: From Weak to Strong Ciphers Block-cipher design paradigm: • Design weak component • Iterate weak component multiple times Sequential composition of weak ciphers M E E E K 1 K 2 K 3 • DES best attack: 242 • 3 DES best attack: 290 C Used for 3 DES, where E = DES is insecure (widespread in the electronic payment sector) Expectation: Breaking construction strictly harder than breaking component Hope: T’ > T! Cannot show this in the standard model under any reasonable assumption on E …

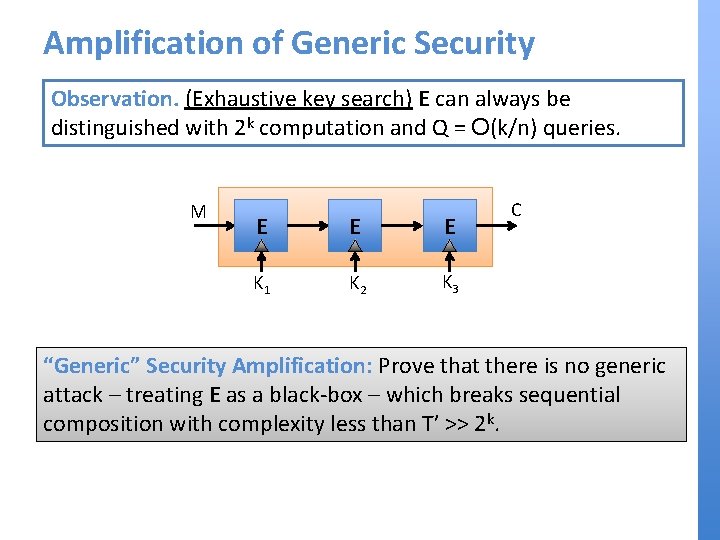
Amplification of Generic Security Observation. (Exhaustive key search) E can always be distinguished with 2 k computation and Q = O(k/n) queries. M E E E K 1 K 2 K 3 C “Generic” Security Amplification: Prove that there is no generic attack – treating E as a black-box – which breaks sequential composition with complexity less than T’ >> 2 k.

The Ideal Cipher Model [Sha 49] k: E uar from ∀SK ∈ {0, 1} SK Two query types: ESK(M) (+, SK, M) the set of all permutations IC §ESKPrimitive queries � “Local” computation -1(C) (-, SK, C) n → {0, 1}n {0, 1} § Construction queries �Key-dependent access to primitive SK (+, SK, M), (-, SK , C) QP queries C QC queries (+, M), (-, C) IC D P IC D 0/1 Definition. C is (QC, QP, e)-strong PRP if ∀(QC, QP)-distinguishers D: Pr[D → 1|left] – Pr[D → 1|right] < e

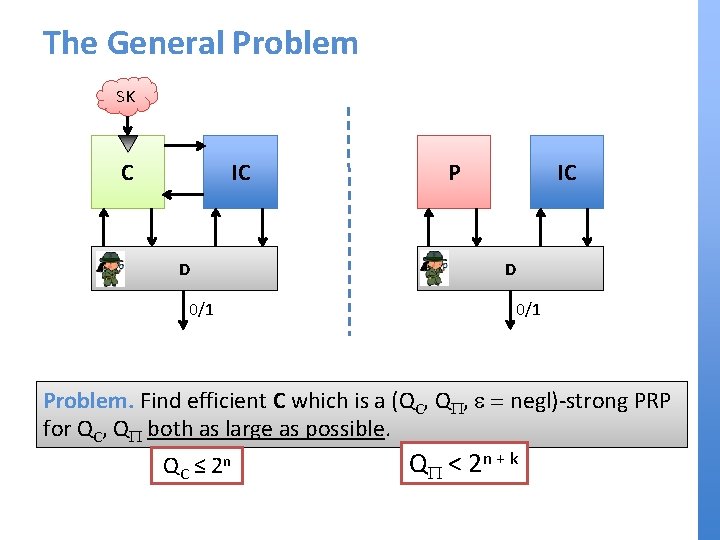
The General Problem SK C IC D 0/1 Problem. Find efficient C which is a (QC, QP, e = negl)-strong PRP for QC, QP both as large as possible. QC ≤ 2 n QP < 2 n + k

Two-fold Sequential Composition z y x E E SK 1 SK 2 SK 1, SK 2 (+, SKSK 1, x) 2, y) EE IC yz (+, x) z

Two-fold Sequential Composition SK 1, SK 2 y’[SK’ 2] x E E z EE P y[SK’ 1] SK’ SK 11 IC SK’ SK 22 D Meet-in-the-middle attack: [Dif. Hel 76] • z ← C(+, x) • ∀SK’ 1: y[SK’ 1] ← IC(+, SK’ 1, x) • ∀SK’ 2: y’[SK’ 2] ← IC(-, SK’ 2, z) • If ∃SK’ 1, SK’ 2 : y[SK’ 1] = y[SK’ 2] then output 1 • Else output 0 Fact 1. Pr[D → 1|left] = 1 0/1 Fact 2. If k < n/2: Pr[D → 1|right] < 1/2

DESX [Rivest, 1984] E SK 1 SK SK 2 Theorem: [Kil. Rog 01] DESX is a (QC, QP, e = negl)-strong PRP if QC * QP < 2 n + k. § § § Result meaningful even when k = 0 [Eve. Man 96] Proof succeeds even if SK 1 = SK 2 [Dun. Kel. Sha 11] Essentially optimal for one-call constructions [Gaz. Tes 12]

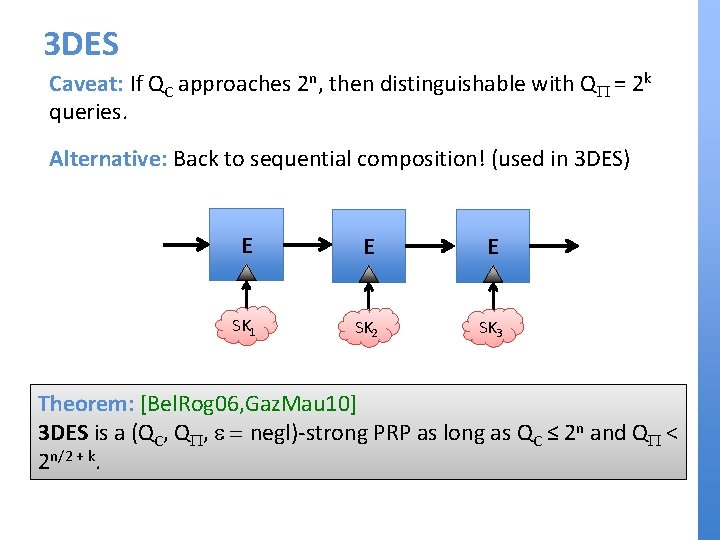
3 DES Caveat: If QC approaches 2 n, then distinguishable with QP = 2 k queries. Alternative: Back to sequential composition! (used in 3 DES) E E E SK 1 SK 2 SK 3 Theorem: [Bel. Rog 06, Gaz. Mau 10] 3 DES is a (QC, QP, e = negl)-strong PRP as long as QC ≤ 2 n and QP < 2 n/2 + k.

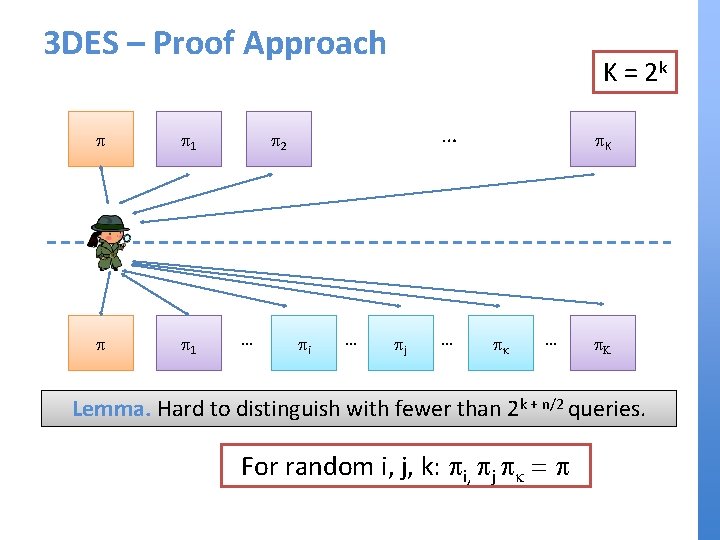
3 DES – Proof Approach p p 1 K = 2 k … p 2 … pi … pj … p. K pk … p. K Lemma. Hard to distinguish with fewer than 2 k + n/2 queries. For random i, j, k: pi, pj pk = p

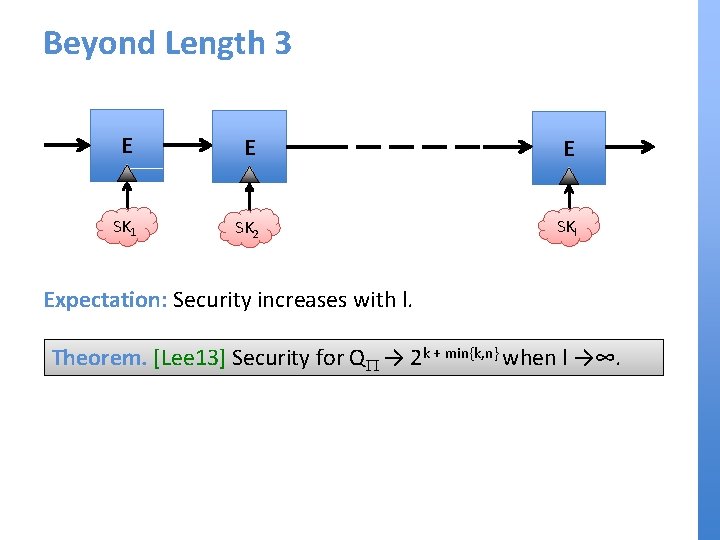
Beyond Length 3 E E E SK 1 SK 2 SKl Expectation: Security increases with l. Theorem. [Lee 13] Security for QP → 2 k + min{k, n} when l →∞.

Increasing Efficiency [Gaz. Tes 12] SK’’ E E SK SK’ Theorem: [Gaz. Tes 12] 2 XOR-Cascade is a (QC, QP, e = negl)-strong PRP if QC ≤ 2 n and QP < 2 k + n/2. [Same security as 3 DES, one block cipher call less]

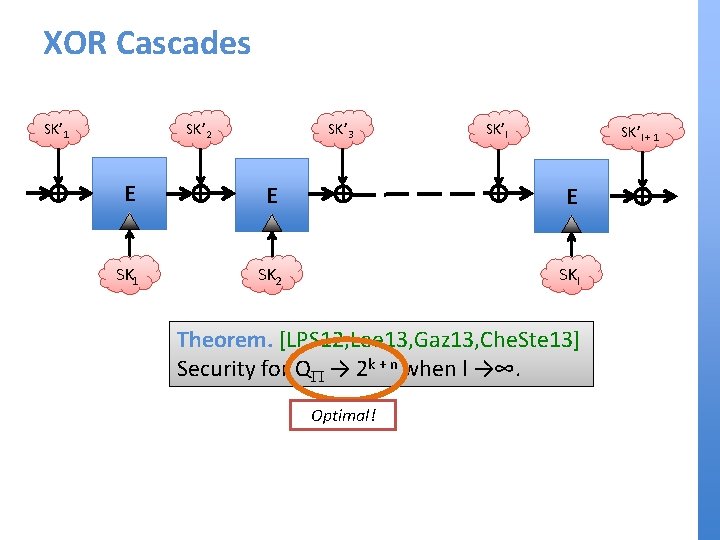
XOR Cascades SK’ 3 SK’ 2 SK’ 1 SK’l + 1 E E E SK 1 SK 2 SKl Theorem. [LPS 12, Lee 13, Gaz 13, Che. Ste 13] Security for QP → 2 k + n when l →∞. Optimal!

Outline Three selected examples: 1 From Weak to Strong Block Ciphers 2 Hash Functions and Key Derivation 3 Building Ideal Primitives

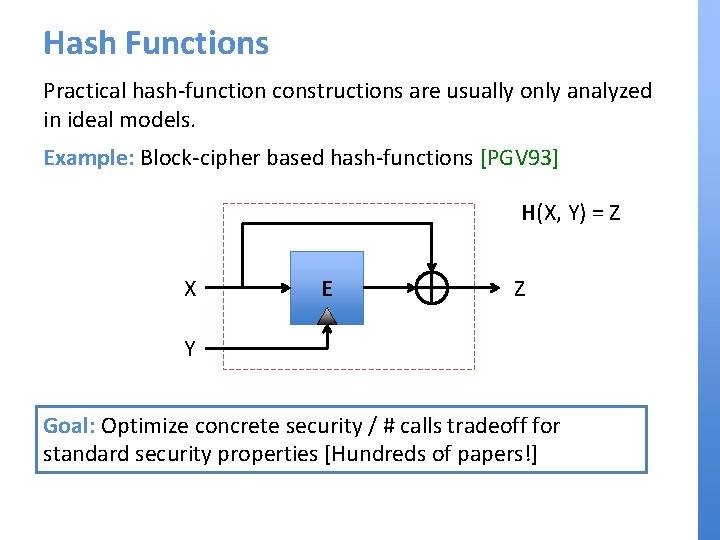
Hash Functions Practical hash-function constructions are usually only analyzed in ideal models. Example: Block-cipher based hash-functions [PGV 93] H(X, Y) = Z X E Z Y Goal: Optimize concrete security / # calls tradeoff for standard security properties [Hundreds of papers!]

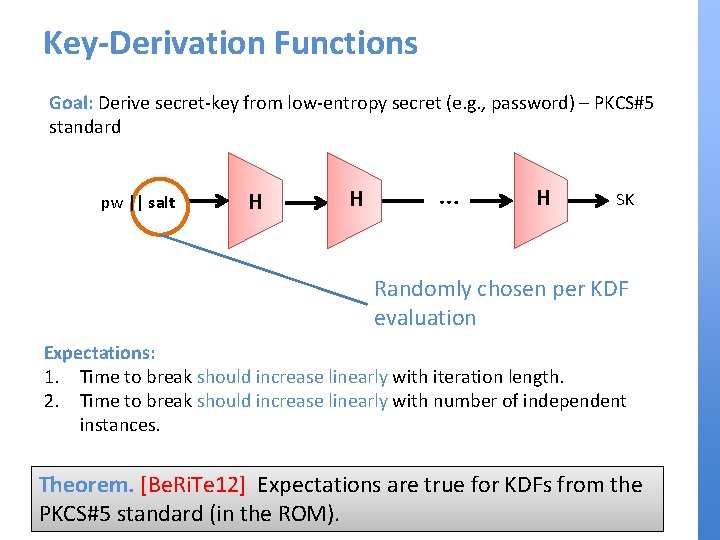
Key-Derivation Functions Goal: Derive secret-key from low-entropy secret (e. g. , password) – PKCS#5 standard pw || salt H H … H SK Randomly chosen per KDF evaluation Expectations: 1. Time to break should increase linearly with iteration length. 2. Time to break should increase linearly with number of independent instances. Theorem. [Be. Ri. Te 12] Expectations are true for KDFs from the PKCS#5 standard (in the ROM).

Outline Three selected examples: 1 From Weak to Strong Block Ciphers 2 Hash Functions and Key Derivation 3 Building Ideal Primitives

So far: Construction C of a primitive Q from a primitive P achieving specific goal, with security proof in ideal-P model. Most ambitious goal. Construction C(. ) using ideal primitive P s. t. C(P) “as good as” ideal primitive Q. “If an application is secure in the ideal-Q model, then it is secure in the ideal-P model, where calls to Q are replaced by calls to C(P). ”

Indifferentiability [Ma. Re. Ho 04] Keyless, deterministic construction C P Q D 0/1 SIM D 0/1 Definition. C (QC, QP, e)-indifferentiable: ∃(efficient) SIM∀D: Pr[D → 1|left] – Pr[D → 1|right] < e [Typically: efficient = poly(QC, QP), e = negl(k)]

Composability [Ma. Re. Ho 04] Arbitrary security game G SIM Q P C G G 0/1 Pr[G → 1|Q] = negl Pr[G → 1|C(P)] = ? Indifferentiability �Pr[G → 1|C(P)] = negl

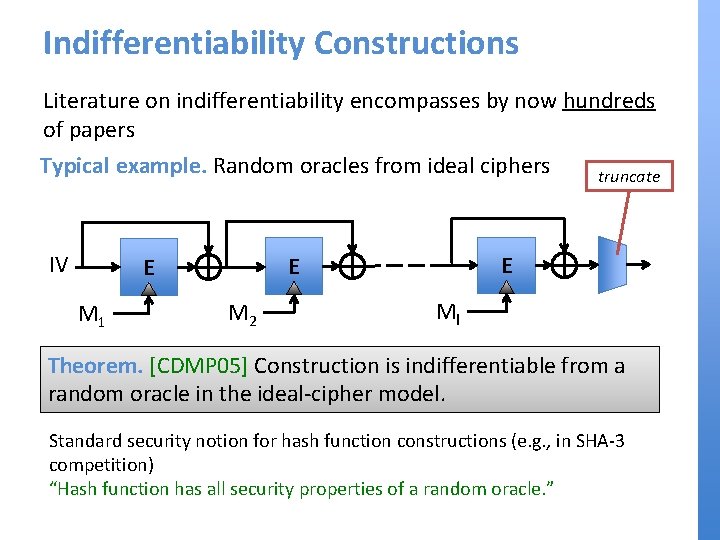
Indifferentiability Constructions Literature on indifferentiability encompasses by now hundreds of papers Typical example. Random oracles from ideal ciphers IV M 1 E E E M 2 truncate Ml Theorem. [CDMP 05] Construction is indifferentiable from a random oracle in the ideal-cipher model. Standard security notion for hash function constructions (e. g. , in SHA-3 competition) “Hash function has all security properties of a random oracle. ”

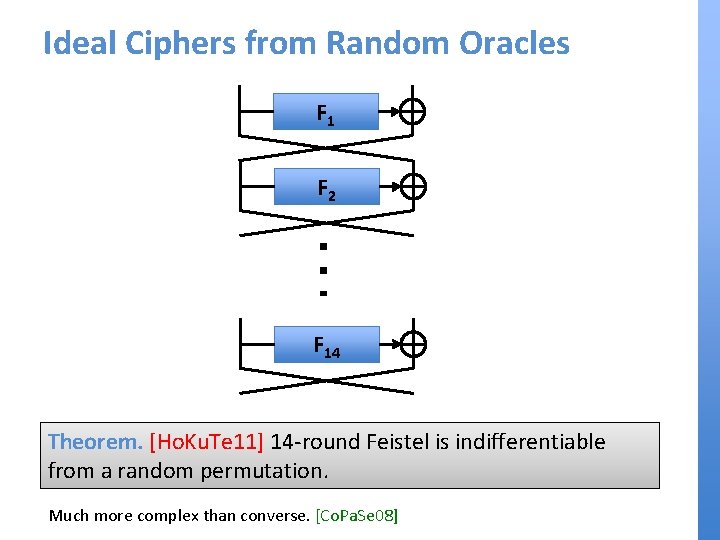
Ideal Ciphers from Random Oracles F 1 F 2 F 14 Theorem. [Ho. Ku. Te 11] 14 -round Feistel is indifferentiable from a random permutation. Much more complex than converse. [Co. Pa. Se 08]

Indifferentiability Constructions Other constructions Random oracles from fixed input-length random oracles with optimal security […, Mau. Tes 07, …, Dod. Ste 11, …] Leads to interesting questions about expander graphs. Ideal ciphers from random permutations [ABDMS 13, Lam. Seu 13]

Multi-Stage Games Q G 1 Examples: • Deterministic encryption • Leakage resilience • … G 2 0/1 Observation. [RSS 11] Indifferentiability does not imply composition for multi-stage games.

Multi-Stage Games New Goal: Find good indifferentiability-like notions with composition properties for multi-stage games. § § Reset indifferentiability [RSS 11]: Distinguisher is allowed to reset simulator. Reset indifferentiability sufficient for secure composition in the multi-stage setting. Many impossibility results: Traditional indifferentiability results are impossible for reset indifferentiability [DGHM 13, BBM 13, …] …

Conclusions § Ideally, we would like to avoid ideal models. § A large number of relevant security questions can only be answered using ideal-model security proofs. § Ideal models give rise to a rich area of works with interesting theoretical questions.

Thank you!

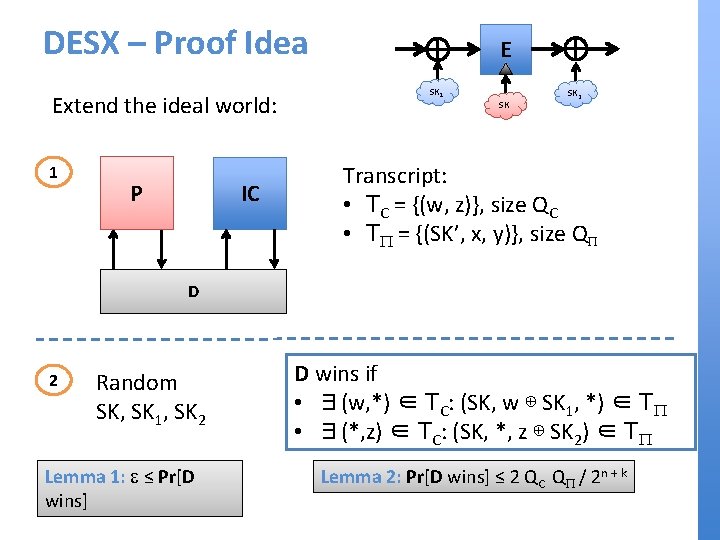
DESX – Proof Idea Extend the ideal world: 1 P IC E SK 1 SK SK 2 Transcript: • TC = {(w, z)}, size QC • TP = {(SK’, x, y)}, size QP D 2 Random SK, SK 1, SK 2 Lemma 1: e ≤ Pr[D wins] D wins if • ∃(w, *) ∈ TC: (SK, w ⊕ SK 1, *) ∈ TP • ∃(*, z) ∈ TC: (SK, *, z ⊕ SK 2) ∈ TP Lemma 2: Pr[D wins] ≤ 2 QC QP / 2 n + k