Public Key Cryptography Public Key Cryptography symmetric key

Public Key Cryptography

Public Key Cryptography symmetric key crypto • requires sender, receiver know shared secret key • Q: how to agree on key in first place (particularly if never “met”)? public key cryptography • radically different approach [Diffie. Hellman 76, RSA 78] • sender, receiver do not share secret key • public encryption key known to all • private decryption key known only to receiver

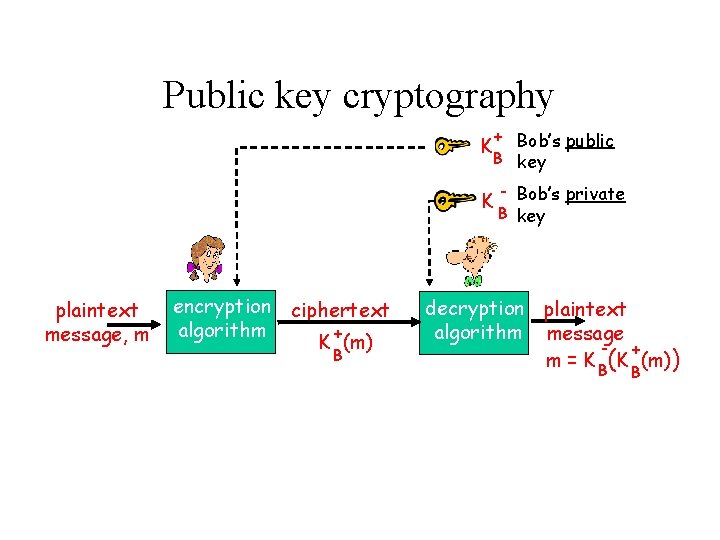
Public key cryptography + Bob’s public B key K K plaintext message, m encryption ciphertext algorithm + K (m) B - Bob’s private B key decryption plaintext algorithm message + m = K B(K (m)) B

Public key encryption algorithms Requirements: 1 2 . . + need KB ( ) and KB ( ) such that - + KB (m)) = m + given public key K B, it should be impossible- to compute private key K B RSA: Rivest, Shamir, Adelson algorithm

RSA: Choosing keys 1. Choose two large prime numbers p, q. (e. g. , 1024 bits each) 2. Compute n = pq, z = (p-1)(q-1) 3. Choose e (with e<n) that has no common factors with z. (e, z are “relatively prime”). 4. Choose d such that ed-1 is exactly divisible by z. (in other words: ed mod z = 1 ). 5. Public key is (n, e). Private key is (n, d). + KB - KB

RSA: Encryption, decryption 0. Given (n, e) and (n, d) as computed above 1. To encrypt bit pattern, m, compute e e c = m mod n (i. e. , remainder when m is divided by n) 2. To decrypt received bit pattern, c, compute d m = c d mod n (i. e. , remainder when c is divided by n) Magic d m = (m e mod n) mod n happens! c

RSA: Why is that m = (m e mod n) d mod n Useful number theory result: If p, q prime and n = pq, then: y y mod (p-1)(q-1) x mod n = x mod n e (m mod n) d mod n = med mod n = m ed mod (p-1)(q-1) mod n (using number theory result above) 1 = m mod n (since we chose ed to be divisible by (p-1)(q-1) with remainder 1 ) = m

RSA: another important property The following property will be very useful later: - + B B K (K (m)) + = m = K (K (m)) B B use public key first, followed by private key use private key first, followed by public key Result is the same!

Public-Key Cryptography Principles • The use of two keys has consequences in: key distribution, confidentiality and authentication. • The scheme has six ingredients (see Figure 3. 7) – – – Plaintext Encryption algorithm Public and private key Ciphertext Decryption algorithm

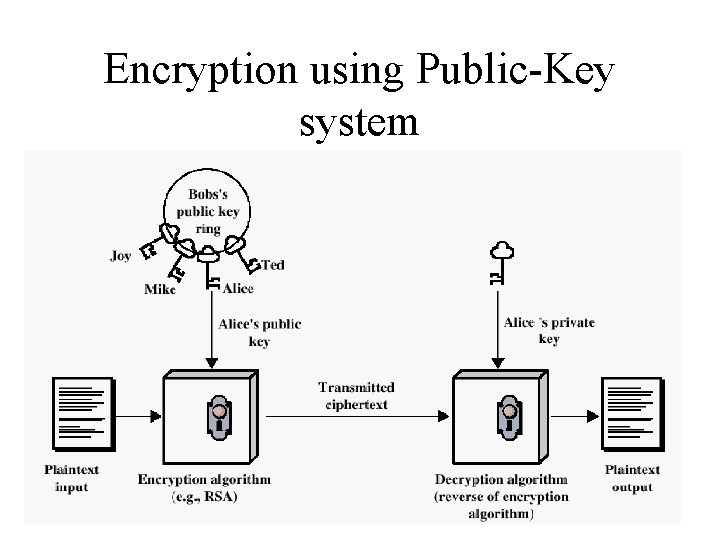
Encryption using Public-Key system

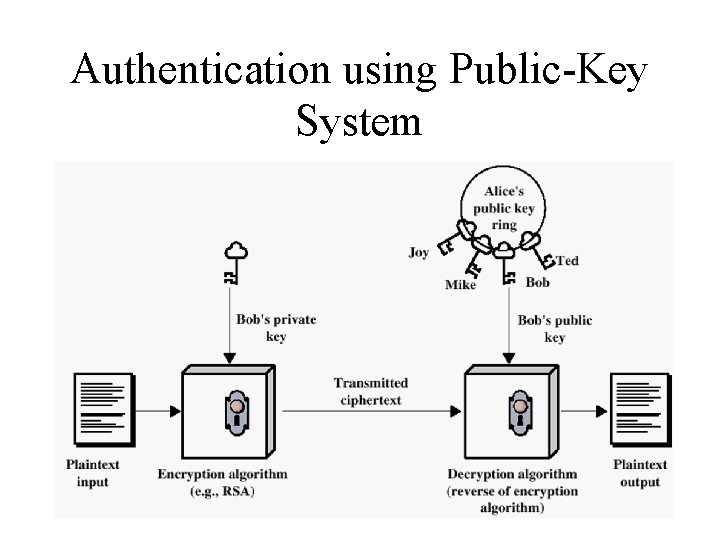
Authentication using Public-Key System

Applications for Public-Key Cryptosystems • Three categories: – Encryption/decryption: The sender encrypts a message with the recipient’s public key. – Digital signature: The sender ”signs” a message with its private key. – Key exchange: Two sides cooperate to exhange a session key.

Requirements for Public-Key Cryptography 1. Computationally easy for a party B to generate a pair (public key KUb, private key KRb) 2. Easy for the sender to generate ciphertext: 3. Easy for the receiver to decrypt ciphertect using private key:

Requirements for Public-Key Cryptography 4. Computationally infeasible to determine private key (KRb) knowing public key (KUb) 5. Computationally infeasible to recover message M, knowing KUb and ciphertext C 6. Either of the two keys can be used for encryption, with the other used for decryption:

Public-Key Cryptographic Algorithms • RSA and Diffie-Hellman • RSA - Ron Rives, Adi Shamir and Len Adleman at MIT, in 1977. – RSA is a block cipher – The most widely implemented • Diffie-Hellman – To exchange securely a secret key – Compute discrete logarithms

The RSA Algorithm – Generation 1. 2. 3. 4. 5. 6. 7. Select p, q Calculate n = p x q Calculate Select integer e Calculate d Public Key Private key Key p and q both prime KU = {e, n} KR = {d, n}

The RSA Algorithm - Encryption • Plaintext: M<n • Ciphertext: C = Me (mod n)

The RSA Algorithm - Decryption • Ciphertext: C • Plaintext: M = Cd (mod n)

RSA Example 1. 2. 3. 4. 5. Select primes: p=17 & q=11 Compute n = pq =17× 11=187 Compute ø(n)=(p– 1)(q-1)=16× 10=160 Select e : gcd(e, 160)=1; choose e=7 Determine d: de mod 160=1 and d < 160 Value is d=23 since 23× 7=161= 10× 160+1 6. Publish public key KU={7, 187} 7. Keep secret private key KR={23, 187}

RSA Example cont • sample RSA encryption/decryption is: • given message M = 88 (nb. 88<187) • encryption: C = 887 mod 187 = 11 • decryption: M = 1123 mod 187 = 88

RSA Key Generation • users of RSA must: – determine two primes at random - p, q – select either e or d and compute the other • primes p, q must not be easily derived from modulus N=p. q – means must be sufficiently large – typically guess and use probabilistic test • exponents e, d are inverses, so use Inverse algorithm to compute the other

RSA Security • three approaches to attacking RSA: – brute force key search (infeasible given size of numbers) – mathematical attacks (based on difficulty of computing ø(N), by factoring modulus N) – timing attacks (on running of decryption)

Diffie-Hellman Key Exchange • first public-key type scheme proposed • by Diffie & Hellman in 1976 along with the exposition of public key concepts – note: now is known that James Ellis (UK CESG) secretly proposed the concept in 1970 • is a practical method for public exchange of a secret key • used in a number of commercial products

Diffie-Hellman Key Exchange • a public-key distribution scheme – cannot be used to exchange an arbitrary message – rather it can establish a common key – known only to the two participants • value of key depends on the participants (and their private and public key information) • based on exponentiation in a finite (Galois) field (modulo a prime or a polynomial) - easy • security relies on the difficulty of computing discrete logarithms (similar to factoring) – hard

Diffie-Hellman Setup • all users agree on global parameters: – large prime integer or polynomial q – α a primitive root mod q • each user (eg. A) generates their key – chooses a secret key (number): x. A < q x. A – compute their public key: y. A = α mod q • each user makes public that key y. A

Diffie-Hellman Key Exchange • shared session key for users A & B is KAB: x x KAB = α A. B mod q x. B = y. A mod q (which B can compute) x. A = y. B mod q (which A can compute) • KAB is used as session key in private-key encryption scheme between Alice and Bob • if Alice and Bob subsequently communicate, they will have the same key as before, unless they choose new public-keys • attacker needs an x, must solve discrete log

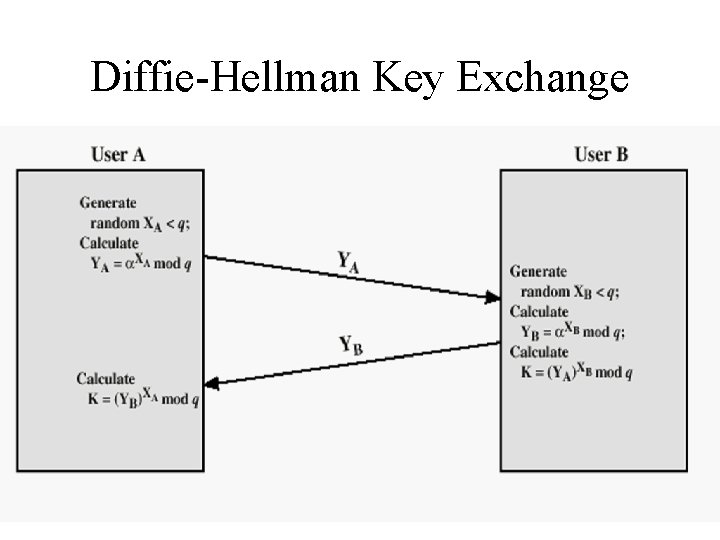
Diffie-Hellman Key Exchange

Diffie-Hellman Example • users Alice & Bob who wish to swap keys: • agree on prime q=353 and α=3 • select random secret keys: – A chooses x. A=97, B chooses x. B=233 • compute public keys: 97 – y. A=3 mod 353 = 40 (Alice) 233 – y. B=3 mod 353 = 248 (Bob) • compute shared session key as: x. A 97 KAB= y. B mod 353 = 248 = 160 x. B 233 KAB= y. A mod 353 = 40 = 160 (Alice) (Bob)

Other Public-Key Cryptographic Algorithms • Digital Signature Standard (DSS) – Makes use of the SHA-1 – Not for encryption or key echange • Elliptic-Curve Cryptography (ECC) – Good for smaller bit size – Low confidence level, compared with RSA – Very complex