Hidden Markov Model Xiaole Shirley Liu STAT 115

Hidden Markov Model Xiaole Shirley Liu STAT 115, STAT 215 1

Outline • Markov Chain • Hidden Markov Model – Observations, hidden states, initial, transition and emission probabilities • Three problems – Pb(observations): forward, backward procedure – Infer hidden states: forward-backward, Viterbi – Estimate parameters: Baum-Welch 2

iid process • iid: independently and identically distributed – Events are not correlated to each other – Current event has no predictive power of future event – E. g. Pb(girl | boy) = Pb(girl), Pb(coin H | H) = Pb(H) Pb(dice 1 | 5) = pb(1) 3

Discrete Markov Chain • Discrete Markov process – Distinct states: S 1, S 2, …Sn – Regularly spaced discrete times: t = 1, 2, … – Markov chain: future state only depends on present state, but not the path to get here – aij transition probability 4

Markov Chain Example 1 • States: exam grade 1 – Pass, 2 – Fail • Discrete times: exam #1, #2, # 3, … • State transition probability • Given PPPFFF, pb of pass in the next exam 5

Markov Chain Example 2 • States: 1 – rain; 2 – cloudy; 3 – sunny • Discrete times: day 1, 2, 3, … • State transition probability • Given 3 at t=1 6

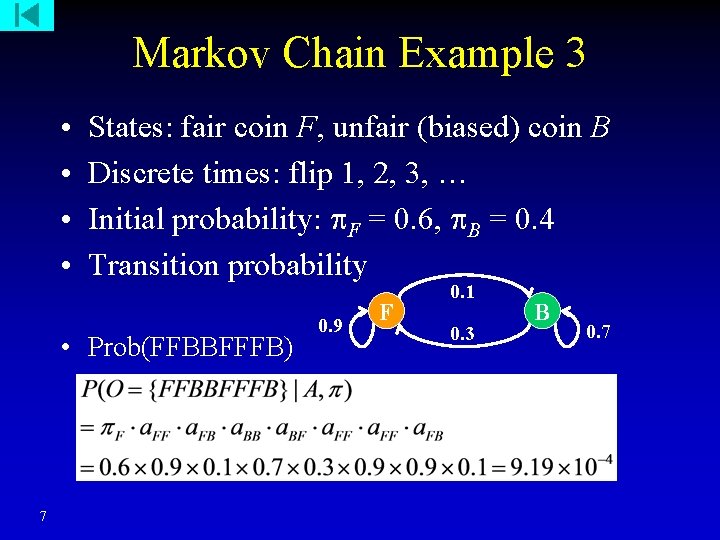
Markov Chain Example 3 • • States: fair coin F, unfair (biased) coin B Discrete times: flip 1, 2, 3, … Initial probability: F = 0. 6, B = 0. 4 Transition probability • Prob(FFBBFFFB) 7 0. 9 F 0. 1 0. 3 B 0. 7

Hidden Markov Model • Coin toss example • Coin transition is a Markov chain • Probability of H/T depends on the coin used • Observation of H/T is a hidden Markov chain (coin state is hidden) 8

Hidden Markov Model • Elements of an HMM (coin toss) – N, the number of states (F / B) – M, the number of distinct observation (H / T) – A = {aij} state transition probability – B = {bj(k)} emission probability – ={ i} initial state distribution • F = 0. 4, B = 0. 6 9

HMM Applications • Stock market: bull/bear market hidden Markov chain, stock daily up/down observed, depends on big market trend • Speech recognition: sentences & words hidden Markov chain, spoken sound observed (heard), depends on the words • Digital signal processing: source signal (0/1) hidden Markov chain, arrival signal fluctuation observed, depends on source • Bioinformatics!! 10

Basic Problems for HMM 1. Given , how to compute P(O| ) observing sequence O = O 1 O 2…OT • • Probability of observing HTTHHHT … Forward procedure, backward procedure 2. Given observation sequence O = O 1 O 2…OT and , how to choose state sequence Q = q 1 q 2…qt • What is the hidden coin behind each flip 1. Forward-backward, Viterbi 3. How to estimate =(A, B, ) so as to maximize P(O| ) 1. How to estimate coin parameters 2. Baum-Welch (Expectation maximization) 11

Problem 1: P(O| ) • Suppose we know the state sequence Q –O=H T –Q=F F T B H F H B T B –Q=B F B B B • Each given path Q has a probability for O 12

Problem 1: P(O| ) • What is the prob of this path Q? –Q=F F B B –Q=B F B B B • Each given path Q has its own probability 13

Problem 1: P(O| ) • Therefore, total pb of O = HTTHHHT • Sum over all possible paths Q: each Q with its own pb multiplied by the pb of O given Q • For path of N long and T hidden states, there are TN paths, unfeasible calculation 14

Solution to Prob 1: Forward Procedure • Use dynamic programming • Summing at every time point • Keep previous subproblem solution to speed up current calculation 15

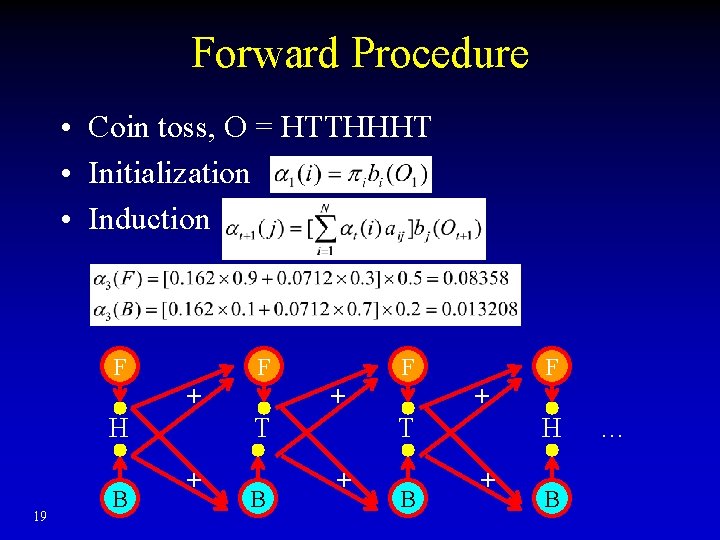
Forward Procedure • Coin toss, O = HTTHHHT • Initialization – Pb of seeing H 1 from F 1 or B 1 F H 16 B T T H …

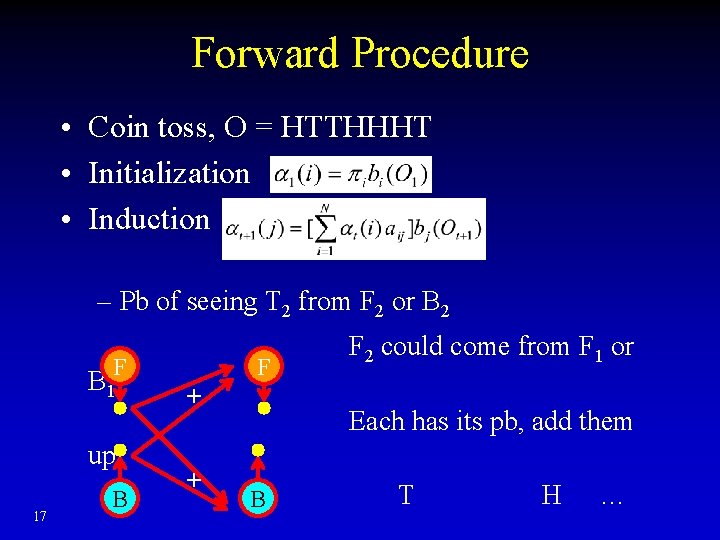
Forward Procedure • Coin toss, O = HTTHHHT • Initialization • Induction – Pb of seeing T 2 from F 2 or B 2 F B 1 17 up H B F + + F 2 could come from F 1 or Each has its pb, add them BT T H …

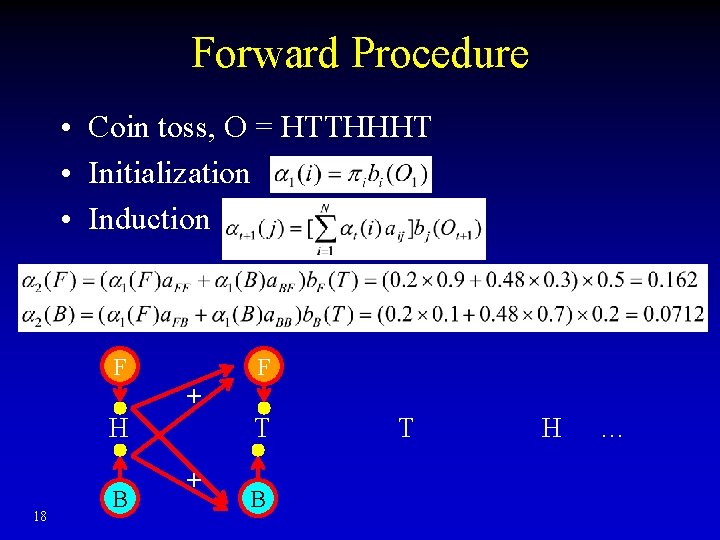
Forward Procedure • Coin toss, O = HTTHHHT • Initialization • Induction F F + H 18 B T + B T H …

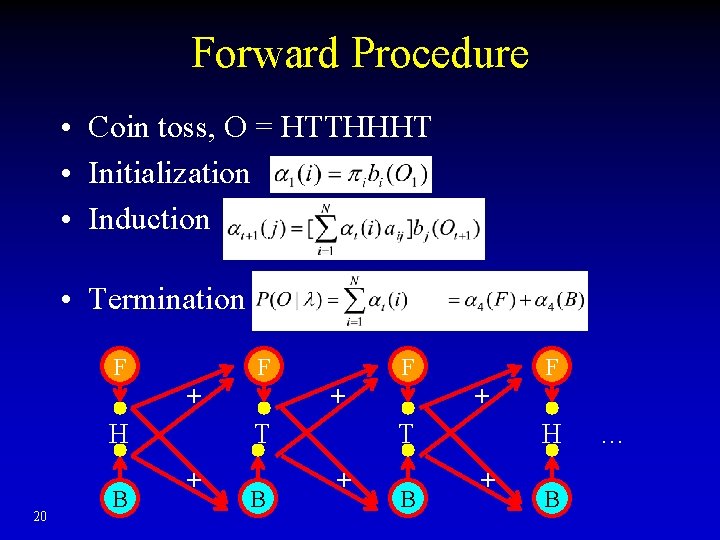
Forward Procedure • Coin toss, O = HTTHHHT • Initialization • Induction F F + H 19 B F + T + B H + B …

Forward Procedure • Coin toss, O = HTTHHHT • Initialization • Induction • Termination F F + H 20 B F + T + B H + B …

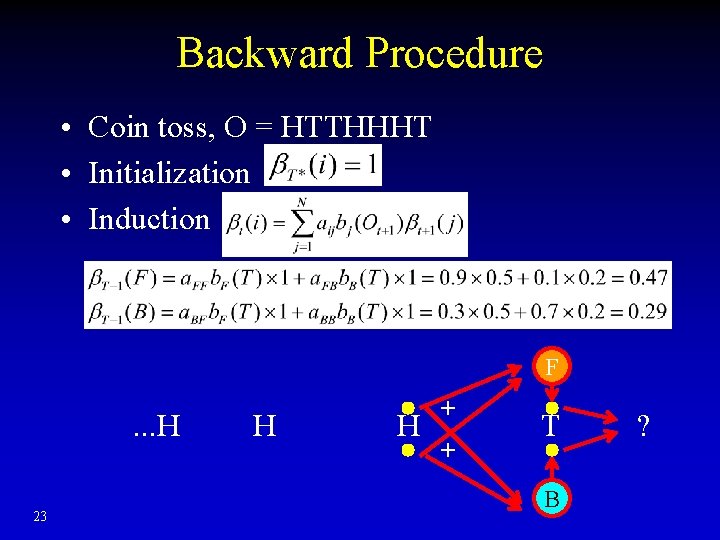
Solution to Prob 1: Backward Procedure • Coin toss, O = HTTHHHT • Initialization • Pb of coin to see certain flip after it F . . . H 21 H H T B

Backward Procedure • Coin toss, O = HTTHHHT • Initialization • Induction • Pb of coin to see certain flip after it 22

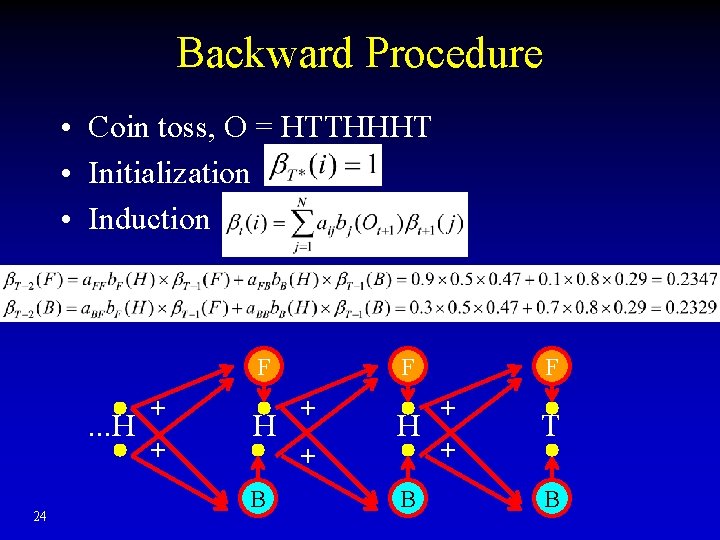
Backward Procedure • Coin toss, O = HTTHHHT • Initialization • Induction F . . . H 23 H H + + T B ?

Backward Procedure • Coin toss, O = HTTHHHT • Initialization • Induction F . . . H 24 + + H F + H + B B F + + T B

Backward Procedure • Coin toss, O = HTTHHHT • Initialization • Induction • Termination • Both forward and backward could be used to solve problem 1, which should give identical results 25

Solution to Problem 2 Forward-Backward Procedure • First run forward and backward separately • Keep track of the scores at every point • Coin toss – α: pb of this coin for seeing all the flips now and before – β: pb of this coin for seeing all the flips after H T T H H H T α 1(F) α 2(F) α 3(F) α 4(F) α 5(F) α 6(F) α 7(F) α 1(B) α 2(B) α 3(B) α 4(B) α 5(B) α 6(B) α 7(B) β 1(F) β 2(F) β 3(F) β 4(F) β 5(F) β 6(F) β 7(F) 26 β 1(B) β 2(B) β 3(B) β 4(B) β 5(B) β 6(B) β 7(B)

Solution to Problem 2 Forward-Backward Procedure • Coin toss • Gives probabilistic prediction at every time point • Forward-backward maximizes the expected number of correctly predicted states (coins) 27

Solution to Problem 2 Viterbi Algorithm • Report the path that is most likely to give the observations • Initiation • Recursion • Termination • Path (state sequence) backtracking 28

Viterbi Algorithm • Observe: HTTHHHT • Initiation 29

Viterbi Algorithm • F H B 30 T T H

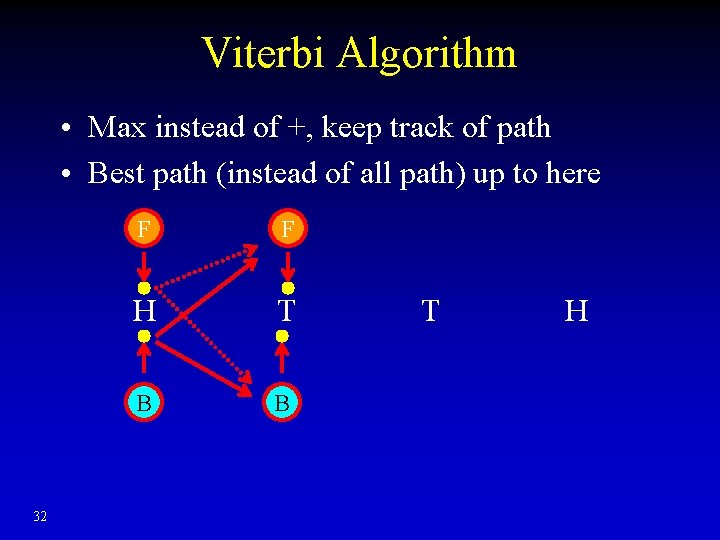
Viterbi Algorithm • Observe: HTTHHHT • Initiation • Recursion 31 Max instead of +, keep track path

Viterbi Algorithm • Max instead of +, keep track of path • Best path (instead of all path) up to here 32 F F H T B B T H

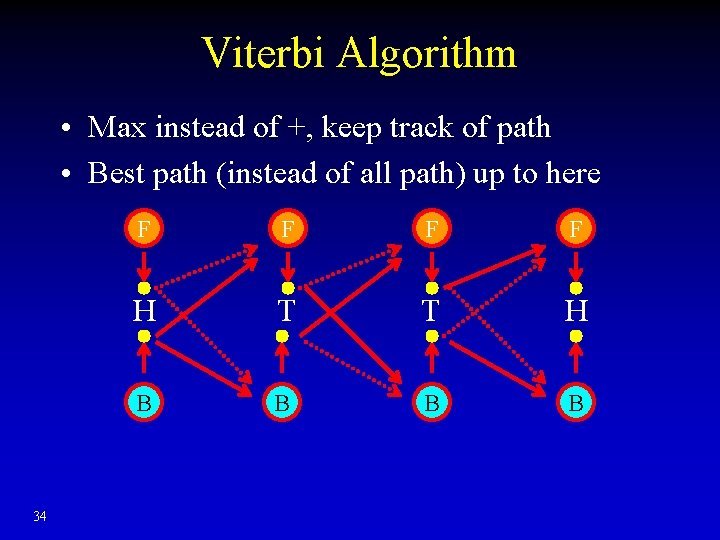
Viterbi Algorithm • Observe: HTTHHHT • Initiation • Recursion 33 Max instead of +, keep track path

Viterbi Algorithm • Max instead of +, keep track of path • Best path (instead of all path) up to here 34 F F H T T H B B

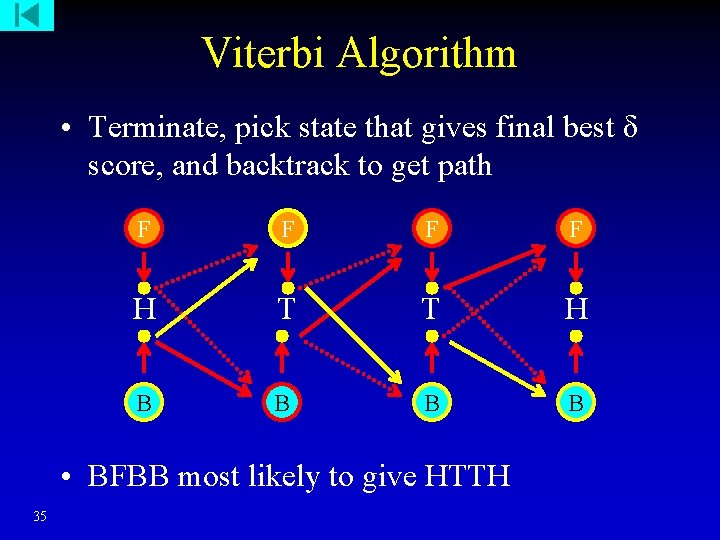
Viterbi Algorithm • Terminate, pick state that gives final best δ score, and backtrack to get path F F H T T H B B • BFBB most likely to give HTTH 35

Solution to Problem 3 • No optimal way to do this, so find local maximum • Baum-Welch algorithm (similar to expectation-maximization) – Random initialize =(A, B, ) – Run forward-backward based on and O – Update =(A, B, ) • : % of F vs B on forward-backward path • A: frequency of F/B transition on the path • B: frequency of H/T emitted by F/B 36

Coin flip without parameters HTHTHHTTHTHTHHTHTT THTHHHHHHHHHTHHHHHHT HTHTHTHHTHHTTTHTHTTHTHHT HTTTHTTHTHTTTTHTTT 37

HMM in Bioinformatics • • 38 Gene prediction Sequence motif finding Protein structure prediction Ch. IP-chip peak calling Chromatin domains Nucleosome positioning on tiling arrays Copy number variation

Summary • Markov Chain • Hidden Markov Model – Observations, hidden states, initial, transition and emission probabilities • Three problems – Pb(observations): forward, backward procedure (give same results) – Infer hidden states: forward-backward (pb prediction at each state), Viterbi (best path) – Estimate parameters: Baum-Welch 39