Hidden Markov Model in Automatic Speech Recognition Z

Hidden Markov Model in Automatic Speech Recognition Z. Fodroczi Pazmany Peter Catholic. Univ.

Outline l Discrete Markov process l Hidden Markov Model ¡ Vitterbi algorithm ¡ Forward algorithm ¡ Parameter estimation ¡ Type of them l HMMs in ASR Systems l Popular models l State of the art and limitation

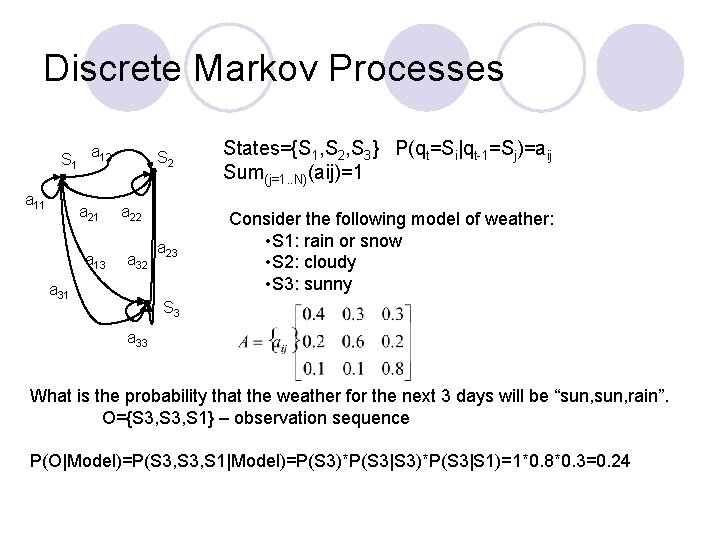
Discrete Markov Processes S 1 a 12 a 11 a 21 a 13 S 2 States={S 1, S 2, S 3} P(qt=Si|qt-1=Sj)=aij Sum(j=1. . N)(aij)=1 a 23 Consider the following model of weather: • S 1: rain or snow • S 2: cloudy • S 3: sunny a 22 a 31 S 3 a 33 What is the probability that the weather for the next 3 days will be “sun, rain”. O={S 3, S 1} – observation sequence P(O|Model)=P(S 3, S 1|Model)=P(S 3)*P(S 3|S 1)=1*0. 8*0. 3=0. 24

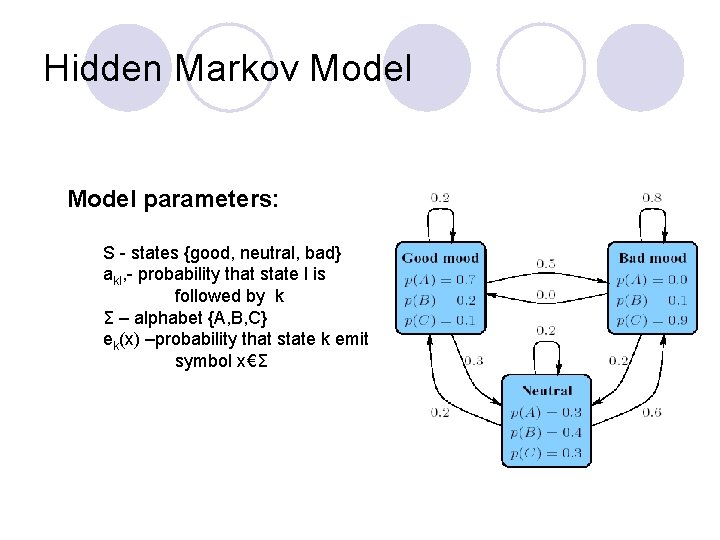
Hidden Markov Model The observation is a probabilistic function of the state. Teacher-mood-model Situation: Your school teacher gave three dierent types of daily homework assignments: ¡ ¡ ¡ A: took about 5 minutes to complete B: took about 1 hour to complete C: took about 3 hours to complete Your teacher did not reveal openly his mood to you daily, but you knew that your teacher was either in a bad, neutral, or a good mood for a whole day. Mood changes occurred only overnight. Question: How were his moods related to the homework type assigned that day?

Hidden Markov Model parameters: S - states {good, neutral, bad} akl, - probability that state l is followed by k Σ – alphabet {A, B, C} ek(x) –probability that state k emit symbol x€Σ

Hidden Markov Model One week, your teacher gave the following homework assignments: ¡ ¡ ¡ Monday: A Tuesday: C Wednesday: B Thursday: A Friday: C Questions: l What did his mood curve look like most likely that week? (Searching for the most probable path – Viterbi algorithm) l What is the probability that he would assign this order of homework assignments? (Probability of a sequence - Forward algorithm) l How do we adjust the model parameters λ(S, aij, ei(x)) to maximize P(O| λ) (create a HMM for a given sequence set)

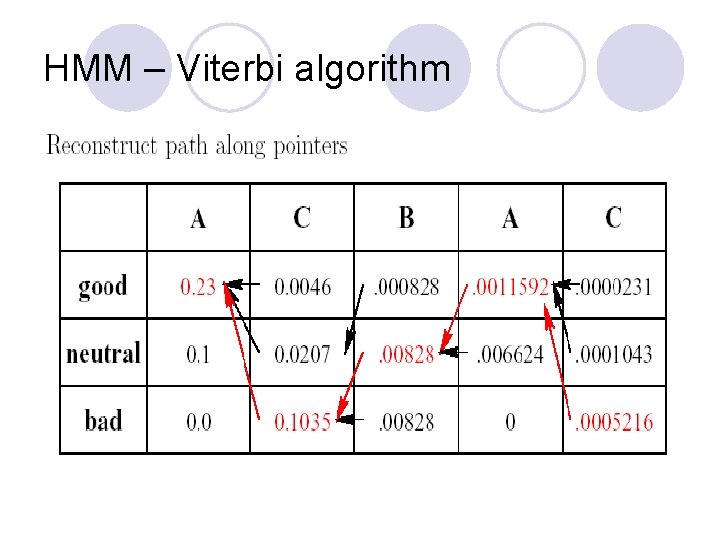
HMM – Viterbi algorithm Given: ¡ Hidden Markov model: S, akl , Σ , ek(x) ¡ Observed symbol sequence E = x 1 x 2, … xn. Most probable path of states that resulted in symbol sequence E. Let vk(i) be the probability of the most probable path of the symbol sequence x 1, x 2, …. xi ending in state k. Then:

HMM – Viterbi algorithm Matrix vk(i), where k€S and 1 <= I <= n. Initialization: vk(1) = ek(x 1)/#states for all states k€S. vl(i) = el(xi)maxk(vk(i - 1)akl) for all states k€S , i >=2. Algorithm l Iteratively build up matrix vk(i). l Store pointers to chosen path. l Probability of most probable path in maximum entry in last column. l Reconstruct path along pointers.

HMM – Viterbi algorithm l Empty table

HMM – Viterbi algorithm

HMM – Viterbi algorithm

HMM – Viterbi algorithm

HMM – Viterbi algorithm

HMM – Viterbi algorithm

HMM – Viterbi algorithm Question: What did his mood curve look like most likely that week? Answer: Most probable mood curve: Day: Mon Tue Wed Thu Fri Assignment: A C B A C Mood: good bad neutral good bad

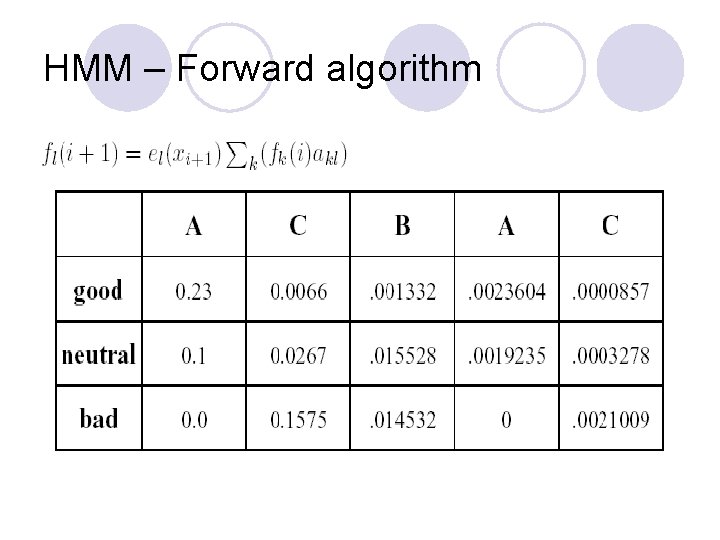
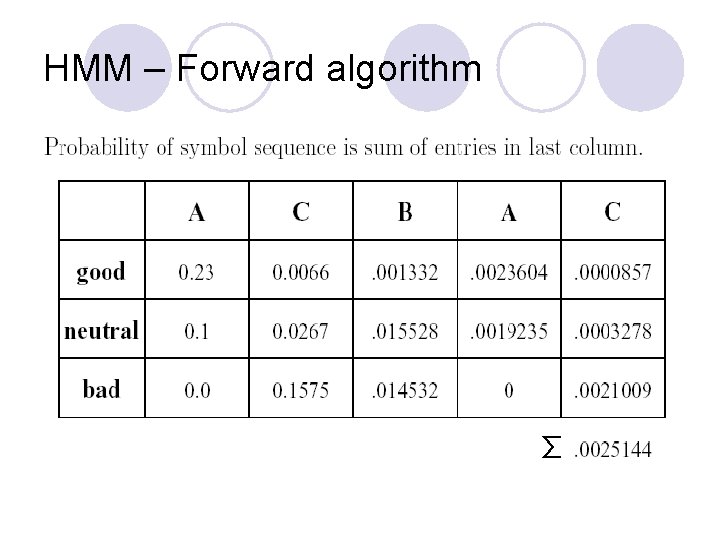
HMM – Forward algorithm Used to test the probability of a sequence. Given: l Hidden Markov model: S, akl, , el(x). l Observed symbol sequence E = x 1; : : : ; xn. What is the probability of E. Let fk(i) be the probability of the symbol sequence x 1, x 2, …. xi ending in state k. Then:

HMM – Forward algorithm Matrix fk(i), where k€S and 1 <= i <= n. l Initialization: fk(1) = ek(x 1)=#states for all states k€S. l fl(i) = el(xi)Pk(fk(i - 1)akl) for all states k€S , i <=2. Algorithm Iteratively build up matrix fk(i). l Probability of symbol sequence is sum of entries in last column. l

HMM – Forward algorithm

HMM – Forward algorithm

HMM – Forward algorithm

HMM – Parameter estimation

HMM – Parameter estimation

HMM – Parameter estimation

Type of HMMs l Till now I was speaking about HMMs with discrete output (finite |Σ|). Extensions: continuous observation probability density function l mixture of Gaussian pdfs l

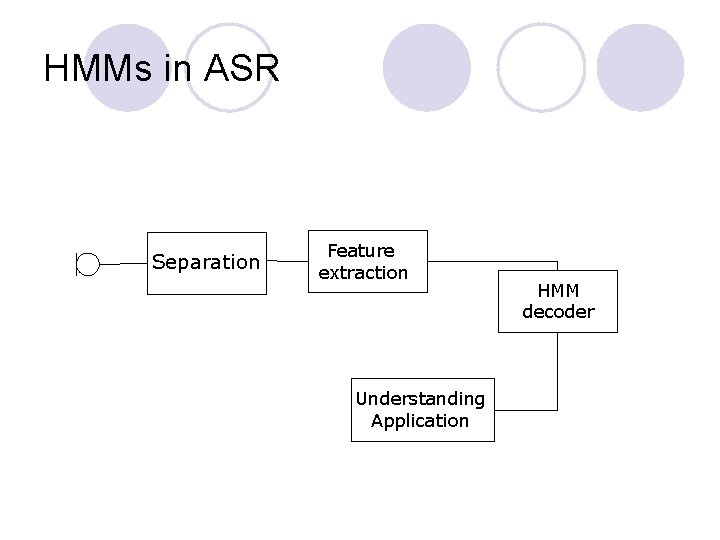
HMMs in ASR Separation Feature extraction Understanding Application HMM decoder

HMMs in ASR How HMM can used to classify feature sequences to known classes. Make a HMM to each class. By determineing the probability of a sequence to the HMMs, we can decide which HMM could most probable generate the sequence. There are several idea what to model: l Isolated word recognition ( HMM for each known word) Usable just on small dictionaries. (digit recognition etc. ) Number of states usually >=4. Left-to-rigth HMM l Monophone acoustic model ( HMM for each phone) ~50 HMM l Triphone acoustic model (HMM for each three phone sequence) 50^3 = 125000 triphones each triphone has 3 state

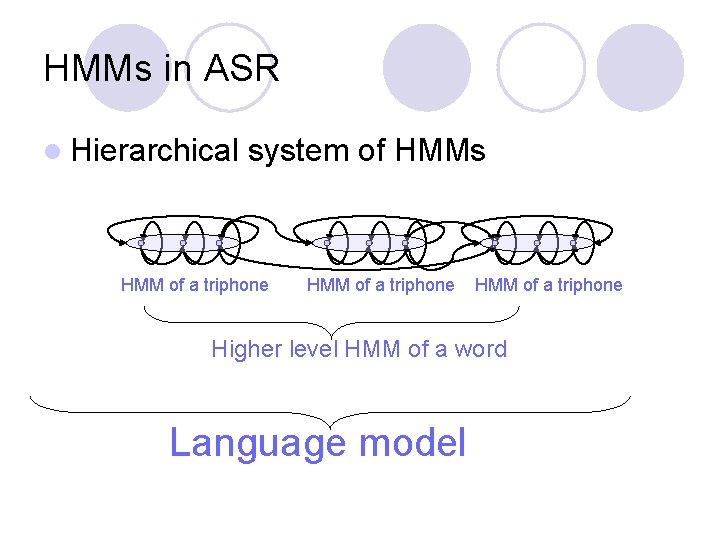
HMMs in ASR l Hierarchical system of HMMs HMM of a triphone Higher level HMM of a word Language model

ASR state of the art Typical state-of-the-art large-vocabulary ASR system: - speaker independent - 64 k word vocabulary - trigram (2 -word context) language model - multiple pronunciations for each word - triphone or quinphone HMM-based acoustic model - 100 -300 X real-time recognition - WER 10%-50%

HMM Limitations Data intensive l Computationally intensive l ¡ 50 phones = 125000 possible triphones l l ¡ 64 k word vocabulary l l ¡ 3 states per triphone 3 Gaussian mixture for each state 262 trillion trigrams 2 -20 phonemes per word in 64 k vocabulary 39 dimensional feature vector sampled every 10 ms l 100 frame per second