Having Fun with Geometry Cavalieris Principle MAFS 912

Having Fun with Geometry Cavalieri’s Principle

MAFS. 912. G-GMD. 1. 1: Give an informal argument for the formulas for the circumference of a circle, area of a circle, volume of a cylinder, pyramid, and cone. Use dissection arguments, Cavalieri’s principle, and informal limit arguments.

Cavalieri’s Principle Historical Note Bonventura Francesco Cavalieri (1598 – 1647) Cavalieri’s work with indivisibles was a precursor to the development of calculus. His method of indivisibles is what is now known as Cavalieri’s Principle.

Activity: Developing a Formula for the Volume of a Cone • Items needed – A partner (let’s work in pairs!) – Ruler – Tape – Scissors – Bag of dry beans – Cone stencil – 2 x sheets of card stock – 12” string

Step One: The Cone • Cut out the cone stencil and create a cone by taping the solid edge to the dashed edge. • Use the string to determine the circumference of the base of the cone in inches. • Measure the slant height of the face of the cone in inches. • Use these two measurements to determine the height of the cone in inches. (5 decimal places)

My Measurements and Solution •

My Measurements and Solution • 3. 375 1. 61144

Step Two: The Cylinder Construct a cylinder that has the same height and circumference as the cone. *** Remember to include an extra half of an inch for overlap before cutting out your cylinder stencil. ***

Step Two: The Cylinder Tape the cylinder to a piece of cardstock so that it won’t slide when being filled.

Step Three: The Beans • Fill the cone completely and accurately with beans. • Pour them into the cylinder. • Repeat until the cylinder is full. What do you observe?

Creating the Formula • What is the formula for the volume of a cylinder? • What is the formula, based on your experiment, for the volume of a cone?

Activity: Comparing the Volume of a Cone and a Pyramid with the Same Base Area and Height

Activity: Comparing the Volume of a Cone and a Pyramid with the Same Base Area and Height Step One Using the radius of the base of the cone in the previous activity, construct a square that has the same area as the base of the cone.

Solution Based on My Measurements •

Step Two • Visualize the pyramid that can be constructed with this square as its base, having the same height as the cone. Optional activity: Have students create the pyramid and confirm that the cone and the pyramid can hold the same volume of beans.

Question We know the base of the cone and the base of the pyramid have the same area, but if we slice the cone and pyramid at a different height in a plane parallel to the base, will these slices have the same area?

Let’s Experiment!

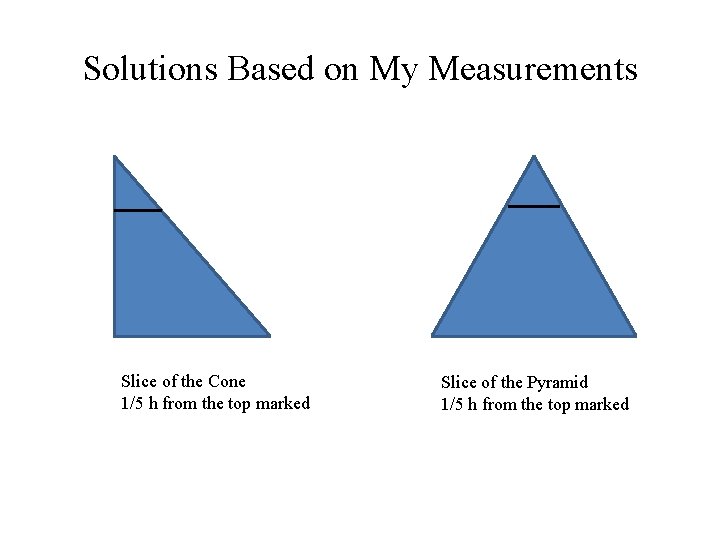
Comparing slices cut by a parallel plane

Comparing Slices •

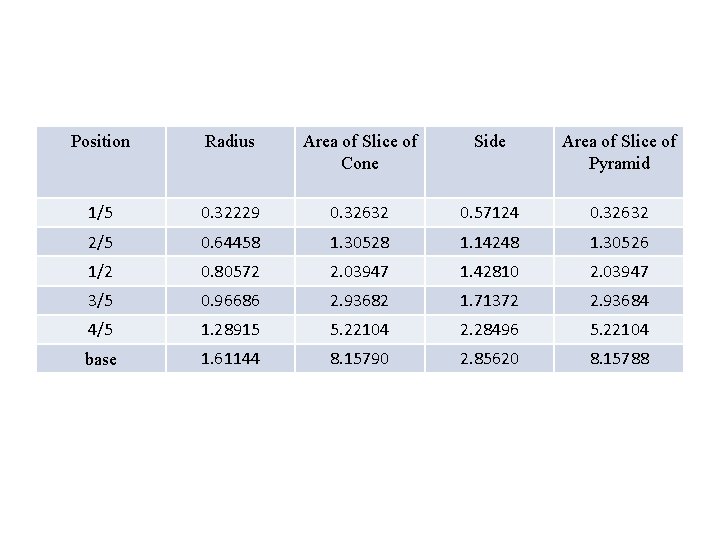
Teamwork To save time, each table will compute the area of a slice of the cone and a slice of the pyramid at one height. Table 1 = 1/5 h (from the top) Table 2 = 2/5 h Table 3 = 1 /2 h Table 4 = 3/5 h Table 5 = 4/5 h (close to bottom)

Results Place your results on the board

Solutions Based on My Measurements Slice of the Cone 1/5 h from the top marked Slice of the Pyramid 1/5 h from the top marked

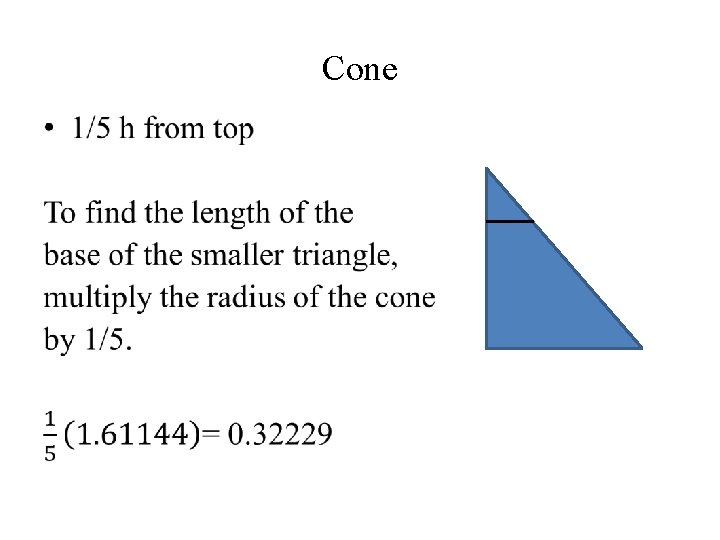
Cone •

Cone •

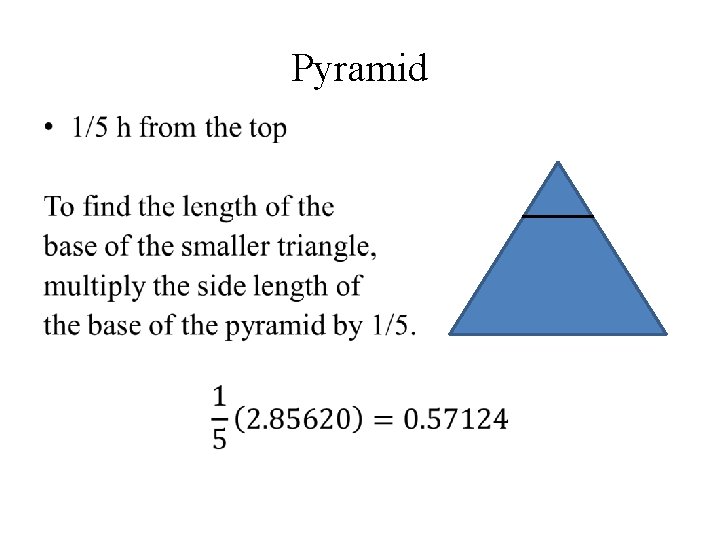
Pyramid •

Pyramid •

Position Radius Area of Slice of Cone Side Area of Slice of Pyramid 1/5 0. 32229 0. 32632 0. 57124 0. 32632 2/5 0. 64458 1. 30528 1. 14248 1. 30526 1/2 0. 80572 2. 03947 1. 42810 2. 03947 3/5 0. 96686 2. 93682 1. 71372 2. 93684 4/5 1. 28915 5. 22104 2. 28496 5. 22104 base 1. 61144 8. 15790 2. 85620 8. 15788

Cavalieri’s Principle • In the three-dimensional case: If two regions are trapped between two parallel planes (imagine one at the top of the cone and pyramid, and one at the bottom), and every plane parallel to these two planes intersects both regions in cross-sections of equal area, then the two regions have equal volume. • Reference: See Wikipedia – You will find some cool mathematics there.

Cavalieri’s Principle • Activity: Take your pennies and stack them neatly on your desk. • Think about the volume of this stack of pennies. • Change the stack so that it is disturbed. (i. e. Push it in the middle, but don’t knock it down. ) • Does this collection of pennies still have the same volume? • Yes! This is Cavalieri’s Principle in action.

Cavalieri’s Principle

Cavalieri’s Principle •

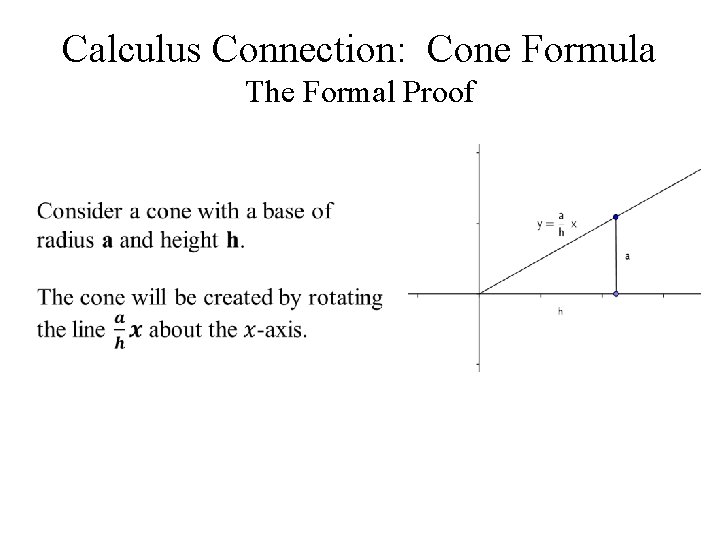
Calculus Connection: Cone Formula The Formal Proof

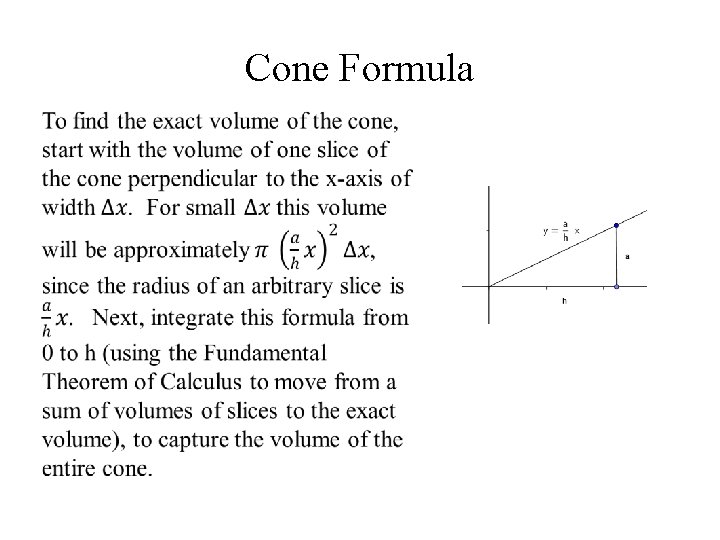
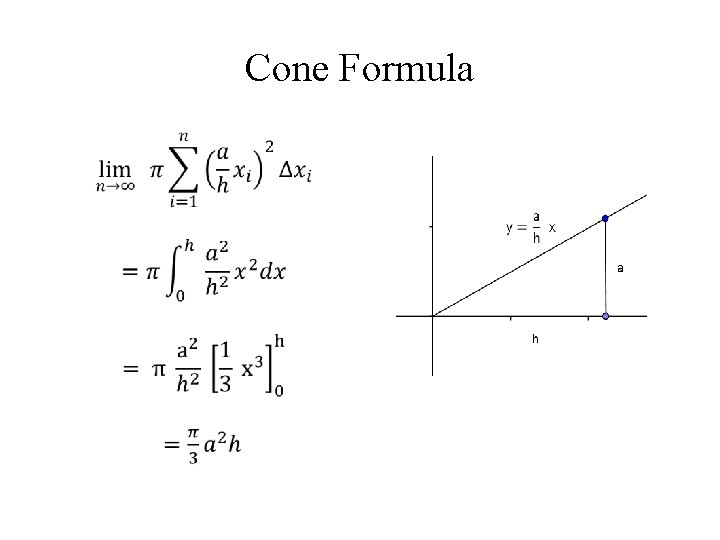
Cone Formula

Cone Formula

Pyramid Formula The formal proof of the formula for the volume of a pyramid is given in the notes for this lesson. The short story … Start with a step-pyramid and find its volume by computing the volume of each step.

Pyramid Formula Then you refine the pyramid, giving it more steps. Each time the base area and height are the same.

Pyramid Formula •

Formal Proof

Formal Proof

Three Important Equalities •

Three Important Equalities •

Three Important Equalities •

Our total volume formula may be transformed as follows: •

Rather Use Applets Than Beans? • Scrolling down this page you will see an animated demonstration of the cube with three pyramids being placed consecutively inside it. This is followed by a discussion with pictures of the cone and pyramid volumes being compared and Cavalieri’s Principle being used. • http: //math. stackexchange. com/questions/62 3/why-is-the-volume-of-a-cone-third-ofthe-volume-of-a-cylinder

Rather Use Applets Than Beans? • This site shows the three pyramids that will fit into a cube and how these pyramids can be transformed into a right square pyramid with the same volume using Cavalieri’s Principle. This is followed by a comparison of a cone to the pyramid and the resulting formula. • http: //nrich. maths. org/1408

Supplemental Material The Napkin Ring Problem http: //en. wikipedia. org/wiki/Napkin_ring_probl em

Supplemental Material The relationship between the formula for a cylinder, cone and sphere: • Given a cylinder and cone with the same radius and height, r and h respectively, such that r is equal to h, and a sphere of radius r = h, the volume of the cylinder minus the volume of the cone is equal to the volume of ½ of the sphere (i. e. the hemisphere). • http: //www. cut-theknot. org/Curriculum/Calculus/Cavalieri. shtml

Questions?