HardyWeinberg Principle HardyWeinberg Principle HardyWeinberg Principle enables us

Hardy-Weinberg Principle

Hardy-Weinberg Principle § § § § Hardy-Weinberg Principle – enables us to calculate and predict allelic and genotypic frequencies Allelic frequency – the frequency of an allele in a population Genotypic frequency – the frequency of a genotype in a population

Hardy-Weinberg § We use p to represent the dominant allele, and q to represent the recessive allele § For allelic frequency: p + q = 1 § So if the frequency of the dominant allele (p) is 0. 75, then the frequency of the recessive allele (q) is… 0. 25

Hardy-Weinberg § For genotypic frequency: p 2 + 2 pq + q 2 = 1 § Where: p 2 = frequency of homozygous dominant 2 pq = frequency of heterozygous q 2 = frequency of homozygous recessive
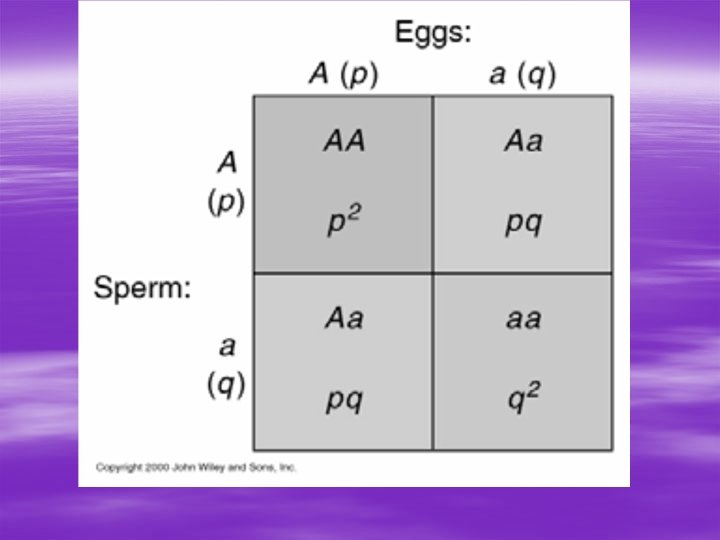

Hardy-Weinberg § SO…for example, if we know the frequency of the homozygous recessive genotype (q 2), we can find the frequency of the recessive allele [√(q 2) = q] § THEN…since we know q, we can find p, then p 2, then 2 pq!

Hardy-Weinberg § Hardy-Weinberg predicts that gene frequencies will remain the same from one generation to the next § However, certain conditions must be met

Hardy-Weinberg – the frequencies of the alleles do not change and – as long as the mating is random, the genotypic frequencies will remain in the proportions p 2 (frequency of AA), 2 pq (frequency of Aa) and q 2 (frequency of aa) where p is the frequency of A and q is the frequency of a – The sum of the genotypic frequencies should be: p 2 + 2 pq + q 2 = 1

Hardy-Weinberg Assumptions § § § 1) Large population 2) Random mating 3) No mutation 4) No migration (in or out of population) 5) No selective pressure

Brachydactyly and evolutionary change § We know the gene for brachydactyl fingers is dominant to normal fingers § A man named Yule suggested that short-fingered people should become more common through time § Godfrey Hardy showed this inference was wrong § Wilhelm Weinberg derived the same solution to the problem independently

The Hardy-Weinberg Law - the most important principle in population genetics § § The law is divided into three parts: a set of assumptions and two major results – In an infinitely large, randomly mating population, free from mutation, migration and natural selection (note there are five assumptions here)

The Hardy-Weinberg Law - the most important principle in population genetics § The incidence of albinism is remarkably common (0. 0043 or 13 in every 3000 Hopis) § Assuming Hardy-Weinberg equilibrium, we can calculate q as the square root of 0. 0043 = 0. 066 § p is therefore equal to 0. 934 § The frequency of heterozygotes in the population is 2 pq = 0. 123 § In other words, 1 in 8 Hopis carries the gene for albinism! § Take-home Lesson: For a rare allele, heterozygotes can be relatively common

Albinism in Hopi Native Americans § The incidence of albinism is remarkably common (0. 0043 or 13 in every 3000 Hopis) § Assuming Hardy-Weinberg equilibrium, we can calculate q as the square root of 0. 0043 = 0. 066 § p is therefore equal to 0. 934 § The frequency of heterozygotes in the population is 2 pq = 0. 123 § In other words, 1 in 8 Hopis carries the gene for albinism! § Take-home Lesson: For a rare allele, heterozygotes can be relatively common

Hardy Weinberg Problem I § § § § § Sickle Cell Anemia – SS = susceptible to malaria but no SCA – ss = non-susceptible but SCA �� mortality – Ss = non-susceptible and no SCA What do we expect proportions of ss? Ss? • E. g. 4% ss - what are proportions of Ss –. 04 = ss = q 2 �� q = √. 04 =. 2 – p = 1 - q = 1 -. 2 =. 8 – Ss = 2 pq = 2(. 8)(. 2) =. 32

Hardy Weinberg Problem II § § § What would it take to increase Ss proportion to 50% (from 32%)? – Ss = 2 pq =. 5 �� pq =. 25 – q = 1 - p �� p (1 -p) =. 25 �� p =. 5 – Which means aa goes to. 25 from. 04, over 6 x

Hardy Weinberg Problem III How many of you can roll your tongues? – A - Yes –B-N

Hardy Weinberg Problem III § § § § What is the percentage of heterozygous tongue-rollers? – Yes = p 2 + 2 pq – No = q 2 – q = √No – p = 1 - q – Heterozygous = 2 pq
- Slides: 17