Section 4 1 Increasing and Decreasing Functions Objectives

Section 4. 1 Increasing and Decreasing Functions

Objectives: 1. To give intervals where a function is increasing or decreasing using interval notation. 2. To identify one-to-one functions using the horizontal line test. 3. To identify monotonic

A closed interval is a segment (interval that includes both endpoints) and is represented with square brackets. An open interval is one that does not include its endpoints and is represented with parentheses.

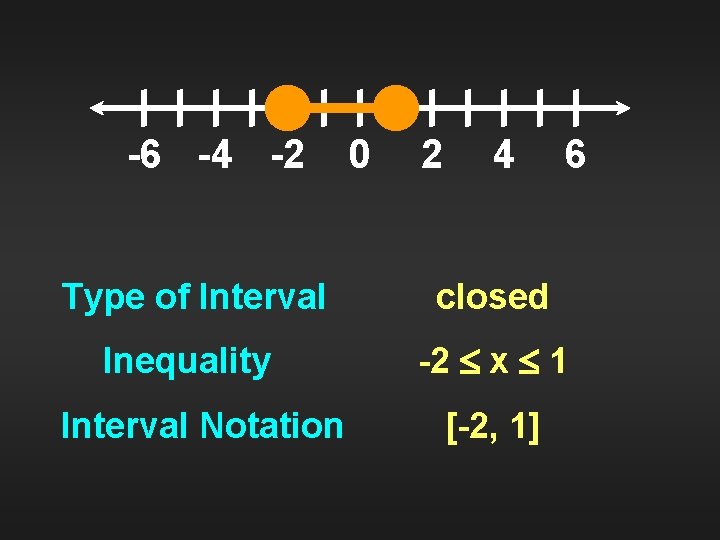
-6 -4 -2 0 2 4 6 Type of Interval closed Inequality -2 x 1 Interval Notation [-2, 1]

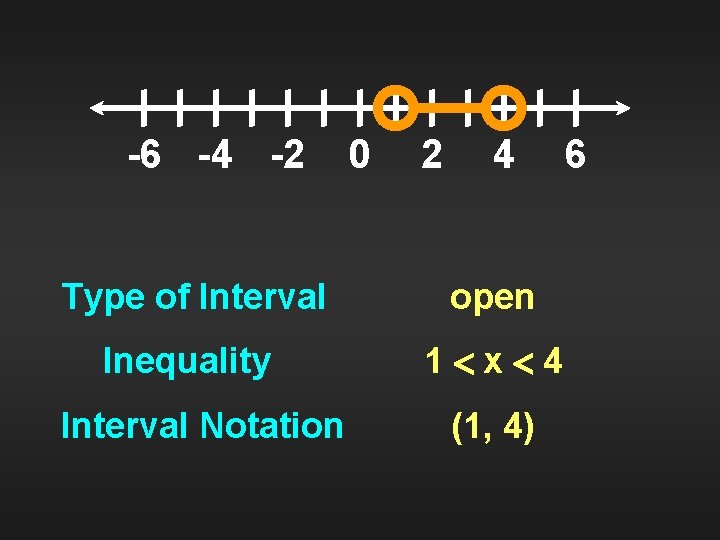
-6 -4 -2 0 2 4 Type of Interval open Inequality 1 x 4 Interval Notation (1, 4) 6

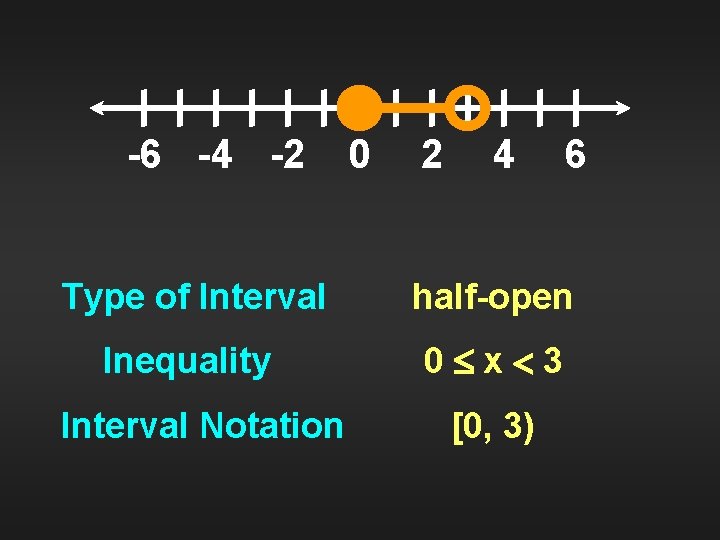
-6 -4 -2 0 2 4 6 Type of Interval half-open Inequality 0 x 3 Interval Notation [0, 3)

EXAMPLE 1 Write the set shown in interval notation. -4 -2 Answer [-2, ∞) 0 2 4

Definition One-to-one correspondence of sets A pairing of elements of two sets so that any element of either set is paired with exactly one element of the other set.

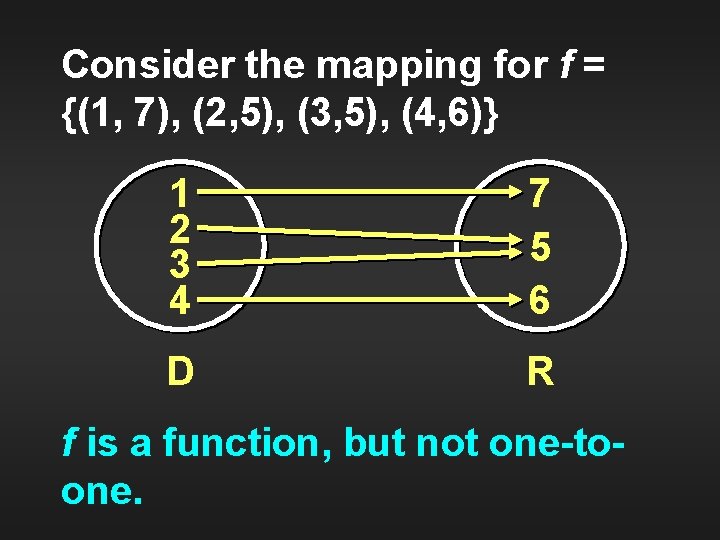
Consider the mapping for f = {(1, 7), (2, 5), (3, 5), (4, 6)} 1 2 3 4 7 5 6 D R f is a function, but not one-toone.

Definition One-to-one function f is one-to -one if and only if f(a) = f(b) implies a = b, a, b Df (domain of f ).

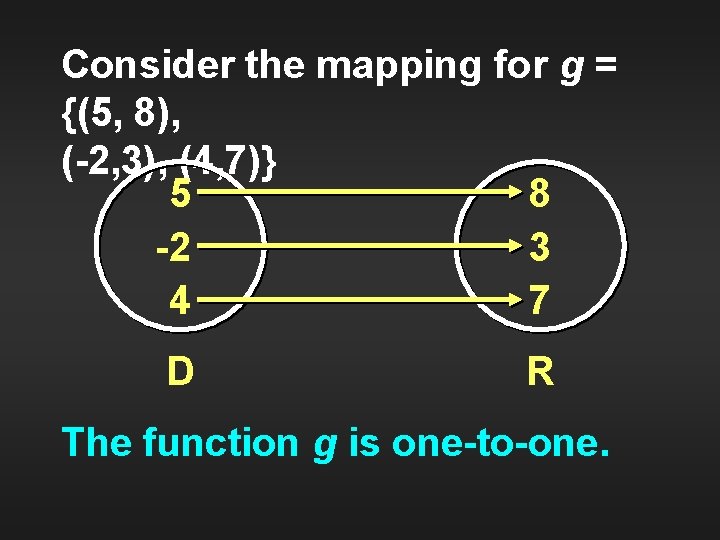
Consider the mapping for g = {(5, 8), (-2, 3), (4, 7)} 5 8 -2 3 4 7 D R The function g is one-to-one.

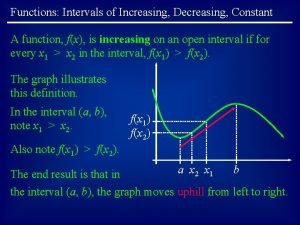
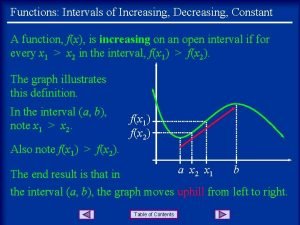
Definition Increasing function A function is increasing if and only if for any two points x 1 and x 2 R, x 1 x 2 implies f(x 1) f(x 2).

Definition Decreasing function A function is decreasing if and only if for any two points x 1 and x 2 R, x 1 x 2 implies f(x 1) f(x 2).

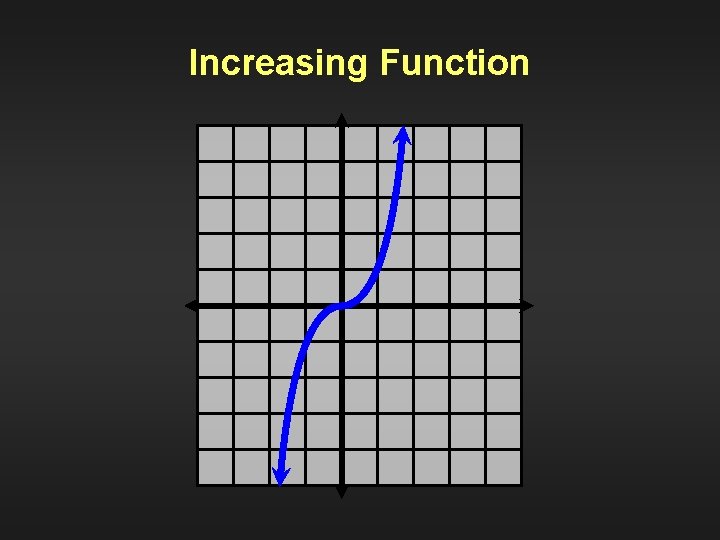
Increasing Function

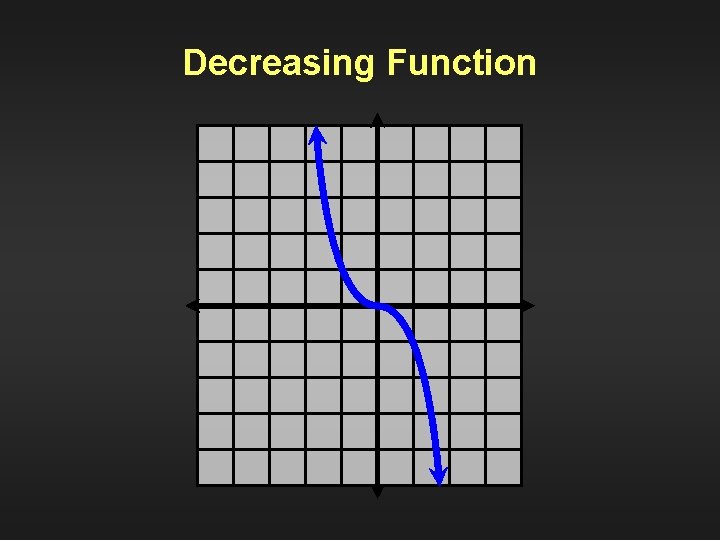
Decreasing Function

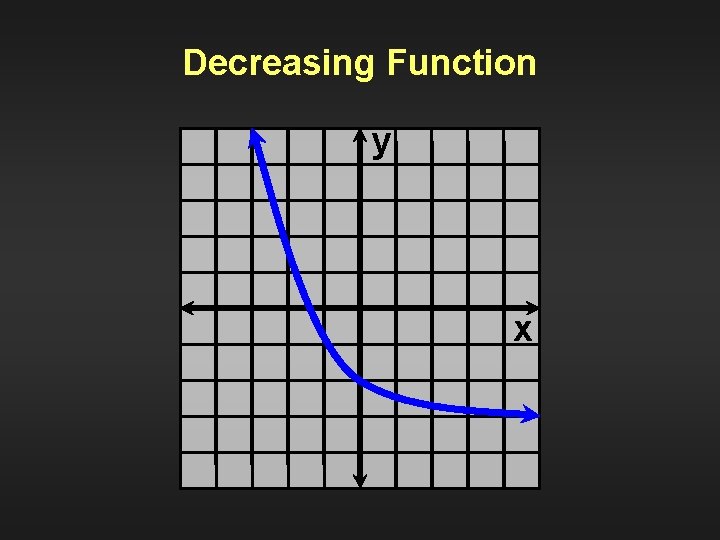
Decreasing Function y x

A function that is increasing over its entire domain or one that is decreasing over its entire domain is a strictly monotonic function.

A monotonic function may remain constant over all or part of its domain. It is either nondecreasing or nonincreasing.

Definition Nondecreasing function A function is nondecreasing if and only if for any two points x 1 and x 2 R, x 1 x 2 implies f(x 1) f(x 2).

Definition Nonincreasing function A function is nonincreasing if and only if for any two points x 1 and x 2 R, x 1 x 2 implies f(x 1) f(x 2).

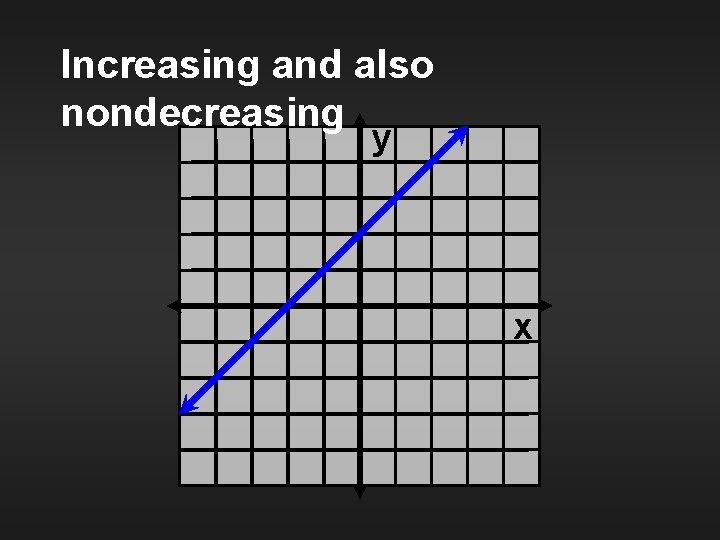
Increasing and also nondecreasing y x

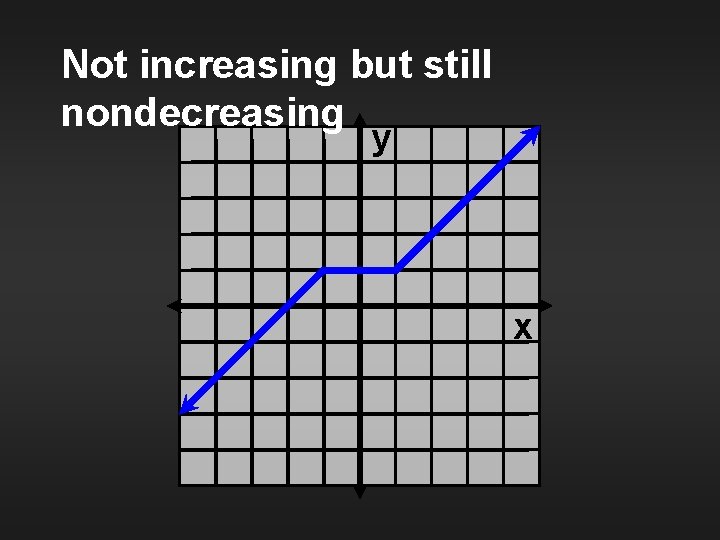
Not increasing but still nondecreasing y x

Homework: pp. 175 -177

►A. Exercises Give the interval notation for each graph. 3. -4 1. (-3, 3) 2. (-3, 3] 3. [-3, 3) 4. [-3, 3] -2 0 2 4

►A. Exercises Give the interval notation for each graph. 5. -4 1. (4, ∞) 2. (4, ∞] 3. [4, ∞) 4. [4, ∞] -2 0 2 4 6

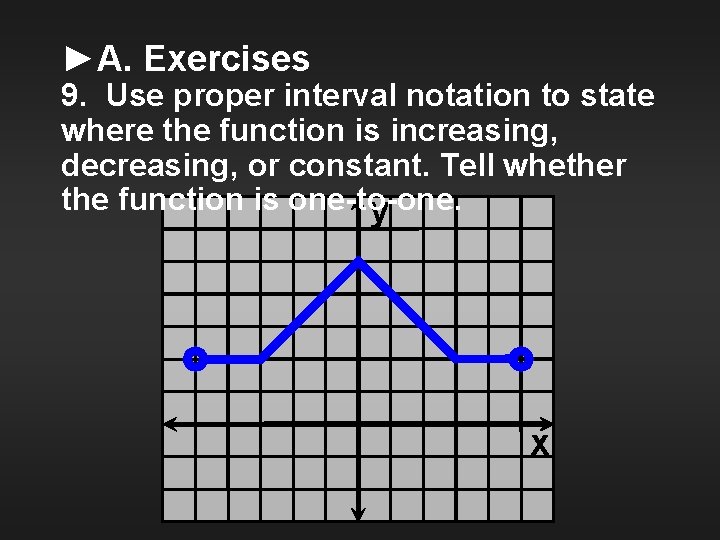
►A. Exercises 9. Use proper interval notation to state where the function is increasing, decreasing, or constant. Tell whether the function is one-to-one. y x

►B. Exercises Graph the following functions. Being as specific as possible, classify each over its entire domain as increasing, decreasing, nonincreasing, nondecreasing, or none. Tell whether the function is one-to-one. 11. y = x 2

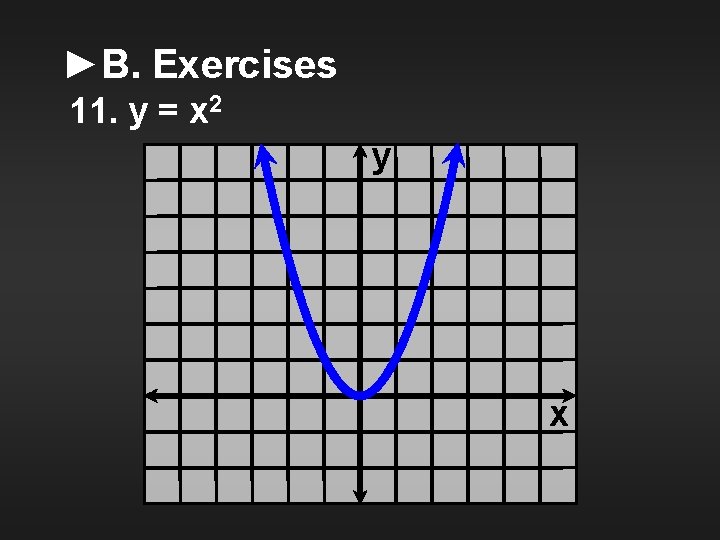
►B. Exercises 11. y = x 2 y x

►B. Exercises Graph the following functions. Being as specific as possible, classify each over its entire domain as increasing, decreasing, nonincreasing, nondecreasing, or none. Tell whether the function is one-to-one. 13. y = 2 -x

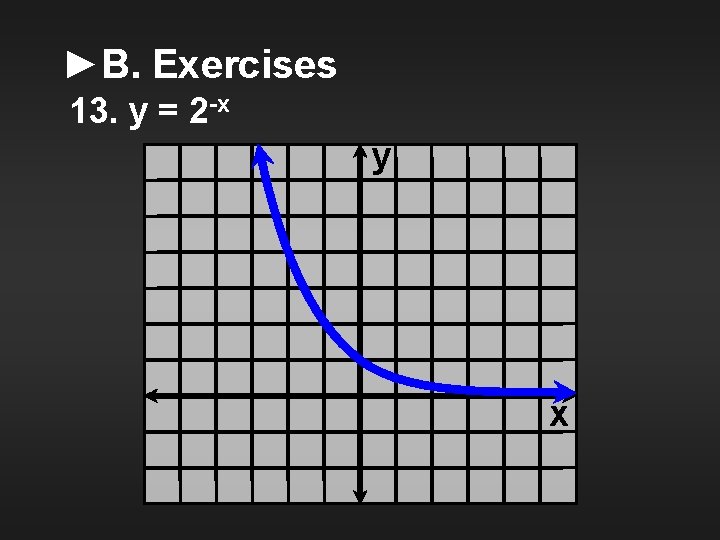
►B. Exercises 13. y = 2 -x y x

►B. Exercises Graph the following functions. Being as specific as possible, classify each over its entire domain as increasing, decreasing, nonincreasing, nondecreasing, or none. Tell whether the function is one-to-one. 15. y = x 2 – 3

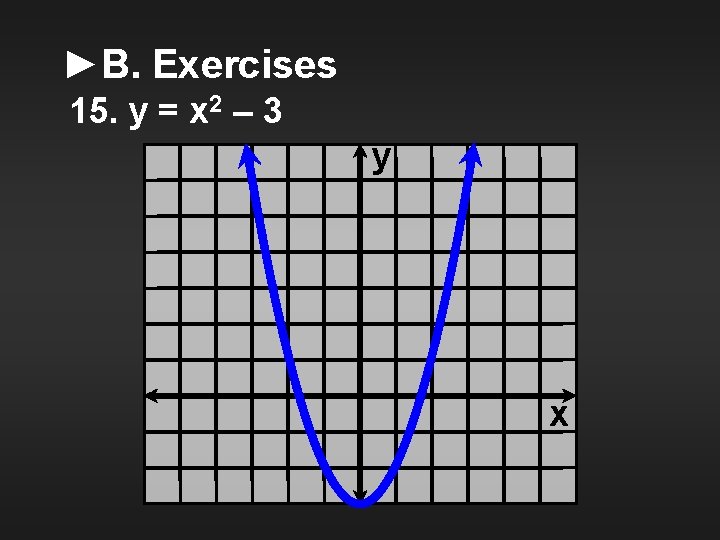
►B. Exercises 15. y = x 2 – 3 y x

►B. Exercises Graph the following functions. Being as specific as possible, classify each over its entire domain as increasing, decreasing, nonincreasing, nondecreasing, or x whether none. Tell if x the 1 function is one-to-one. x + 2 if x 1 19. y =

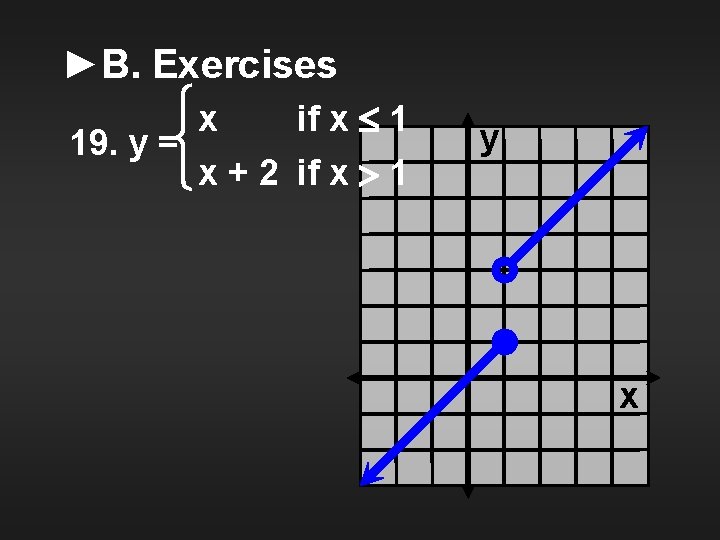
►B. Exercises x if x 1 19. y = x + 2 if x 1 y x

■ Cumulative Review Without graphing, classify each type of function and evaluate it for x = 3. 2 27. f(x) = sin x

■ Cumulative Review Without graphing, classify each type of function and evaluate it for x = 3. 28. g(x) = x 2 + 4 x + 4

■ Cumulative Review Without graphing, classify each type of function and evaluate it for x = 3. 29. h(x) = 5 ● 2 x

■ Cumulative Review Without graphing, classify each type of function and evaluate it for x = 3. 2, x 3 2 x , x 3 30. k(x) =

■ Cumulative Review Without graphing, classify each type of function and evaluate it for x 2 + x – 1 x = 3. x 3 – 2 x 2 – x + 5 31. q(x) =