Section 2 1 Increasing Decreasing and Piecewise Functions













- Slides: 17

Section 2. 1 Increasing, Decreasing, and Piecewise Functions; Applications Copyright © 2017, 2013, 2009 Pearson Education, Inc.

Objectives Graph functions, looking for intervals on which the function is increasing, decreasing, or constant, and estimate relative maxima and minima. · Given an application, find a function that models the application; find the domain of the function and function values, and then graph the function. · Graph functions defined piecewise. · Copyright © 2017, 2013, 2009 Pearson Education, Inc. Slide 2. 1 - 2

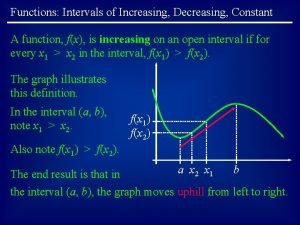
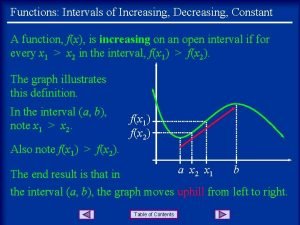
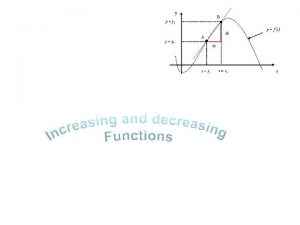
Increasing, Decreasing, and Constant Functions On a given interval, if the graph of a function rises from left to right, it is said to be increasing on that interval. If the graph drops from left to right, it is said to be decreasing. If the function values stay the same from left to right, the function is said to be constant. Copyright © 2017, 2013, 2009 Pearson Education, Inc. Slide 2. 1 - 3

Definitions A function f is said to be increasing on an open interval I, if for all a and b in that interval, a < b implies f(a) < f(b). Copyright © 2017, 2013, 2009 Pearson Education, Inc. Slide 2. 1 - 4

Definitions continued A function f is said to be decreasing on an open interval I, if for all a and b in that interval, a < b implies f(a) > f(b). Copyright © 2017, 2013, 2009 Pearson Education, Inc. Slide 2. 1 - 5

Definitions continued A function f is said to be constant on an open interval I, if for all a and b in that interval, f(a) = f(b). Copyright © 2017, 2013, 2009 Pearson Education, Inc. Slide 2. 1 - 6

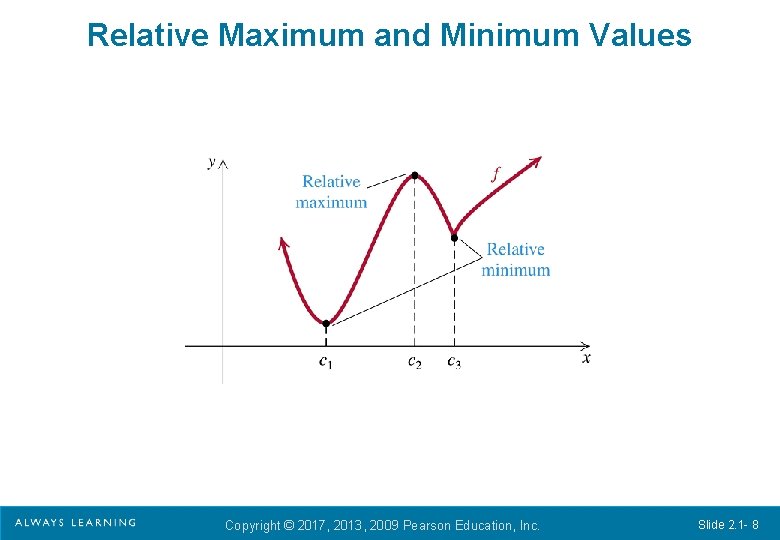
Relative Maximum and Minimum Values Suppose that f is a function for which f (c) exists for some c in the domain of f. Then: f (c) is a relative maximum if there exists an open interval I containing c such that f (c) > f (x), for all x in I where x c; and f (c) is a relative minimum if there exists an open interval I containing c such that f (c) < f (x), for all x in I where x c. Copyright © 2017, 2013, 2009 Pearson Education, Inc. Slide 2. 1 - 7

Relative Maximum and Minimum Values Copyright © 2017, 2013, 2009 Pearson Education, Inc. Slide 2. 1 - 8

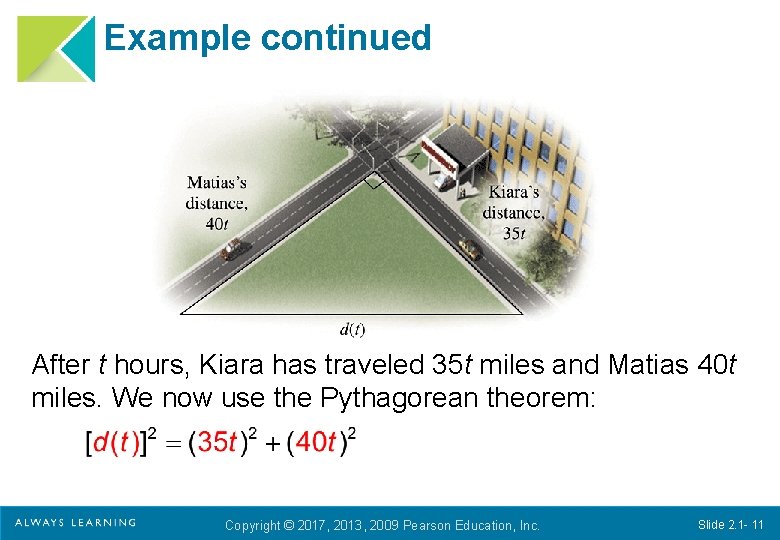
Example Car Distance. Two nurses, Kiara and Matias, drive away from a hospital at right angles to each other. Kiara’s speed is 35 mph and Matias’s is 40 mph. Express the distance between the cars as a function of time, d(t). b) Find the domain of the function. a) Copyright © 2017, 2013, 2009 Pearson Education, Inc. Slide 2. 1 - 9

Example continued Solution Suppose that 1 hr goes by. At that time, Kiara has traveled 35 mi and Matias has traveled 40 mi. We can use the Pythagorean theorem to find the distance between them. The distance would be the length of the hypotenuse of a right triangle with legs measuring 35 mi and 40 mi. After 2 hr, the triangle’s legs would measure 70 mi, and 80 mi. Noting that the distances will always be changing, we make a drawing and let t = time, in hours, that Kiara and Matias have been driving since leaving the hospital. Copyright © 2017, 2013, 2009 Pearson Education, Inc. Slide 2. 1 - 10

Example continued After t hours, Kiara has traveled 35 t miles and Matias 40 t miles. We now use the Pythagorean theorem: Copyright © 2017, 2013, 2009 Pearson Education, Inc. Slide 2. 1 - 11

Example continued Because distance must be nonnegative, we need to consider only the positive square root when solving for d(t): Thus, d(t) = 53. 15 t, t ≥ 0. b. ) Since the time traveled, t must be nonnegative, the domain is the set of nonnegative real numbers [0, ∞). Copyright © 2017, 2013, 2009 Pearson Education, Inc. Slide 2. 1 - 12

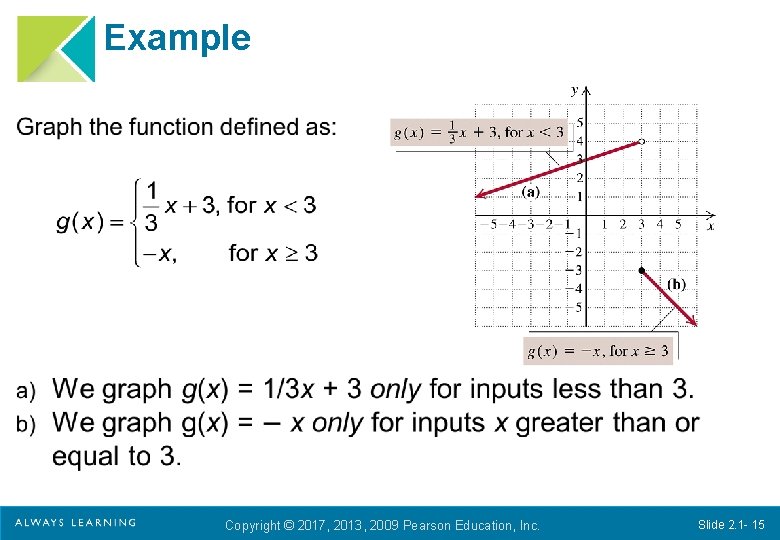
Example Copyright © 2017, 2013, 2009 Pearson Education, Inc. Slide 2. 1 - 13

Example continued Copyright © 2017, 2013, 2009 Pearson Education, Inc. Slide 2. 1 - 14

Example Copyright © 2017, 2013, 2009 Pearson Education, Inc. Slide 2. 1 - 15

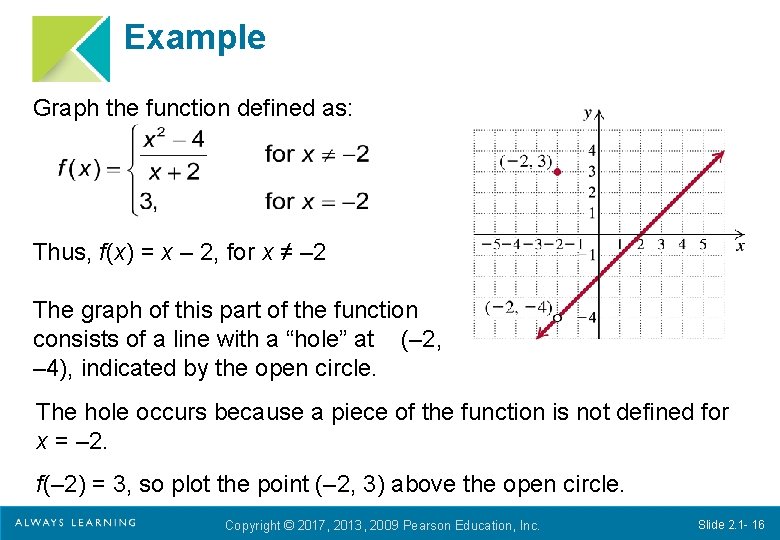
Example Graph the function defined as: Thus, f(x) = x – 2, for x ≠ ‒ 2 The graph of this part of the function consists of a line with a “hole” at (‒ 2, ‒ 4), indicated by the open circle. The hole occurs because a piece of the function is not defined for x = ‒ 2. f(‒ 2) = 3, so plot the point (‒ 2, 3) above the open circle. Copyright © 2017, 2013, 2009 Pearson Education, Inc. Slide 2. 1 - 16

Greatest Integer Function = the greatest integer less than or equal to x. The greatest integer function pairs the input with the greatest integer less than or equal to that input. – 4 Copyright © 2017, 2013, 2009 Pearson Education, Inc. 0 Slide 2. 1 - 17
 Increasing decreasing and piecewise functions
Increasing decreasing and piecewise functions Aims and objectives of increasing and decreasing functions
Aims and objectives of increasing and decreasing functions Lesson 4 increasing and decreasing functions
Lesson 4 increasing and decreasing functions Lesson 5 increasing and decreasing functions
Lesson 5 increasing and decreasing functions Strictly increasing and decreasing functions
Strictly increasing and decreasing functions Increasing and decreasing intervals
Increasing and decreasing intervals Claim of value examples
Claim of value examples How to find increasing and decreasing intervals on a graph
How to find increasing and decreasing intervals on a graph Removable and nonremovable discontinuity
Removable and nonremovable discontinuity Increasing and decreasing intervals
Increasing and decreasing intervals Increasing and decreasing recipes
Increasing and decreasing recipes Intervals of a parabola
Intervals of a parabola Increasing at a decreasing rate
Increasing at a decreasing rate Increasing at a decreasing rate
Increasing at a decreasing rate Absolute value piecewise function
Absolute value piecewise function Piecewise function in real life situation
Piecewise function in real life situation Integral of piecewise function
Integral of piecewise function Definition of piecewise function
Definition of piecewise function