Section 2 1 Increasing Decreasing and Piecewise Functions

Section 2. 1 Increasing, Decreasing, and Piecewise Functions; Applications Copyright © 2013, 2009, 2006, 2001 Pearson Education, Inc.

Objectives Graph functions, looking for intervals on which the function is increasing, decreasing, or constant, and estimate relative maxima and minima. · Given an application, find a function that models the application; find the domain of the function and function values, and then graph the function. · Graph functions defined piecewise. ·

Increasing, Decreasing, and Constant Functions On a given interval, if the graph of a function rises from left to right, it is said to be increasing on that interval. If the graph drops from left to right, it is said to be decreasing. If the function values stay the same from left to right, the function is said to be constant.

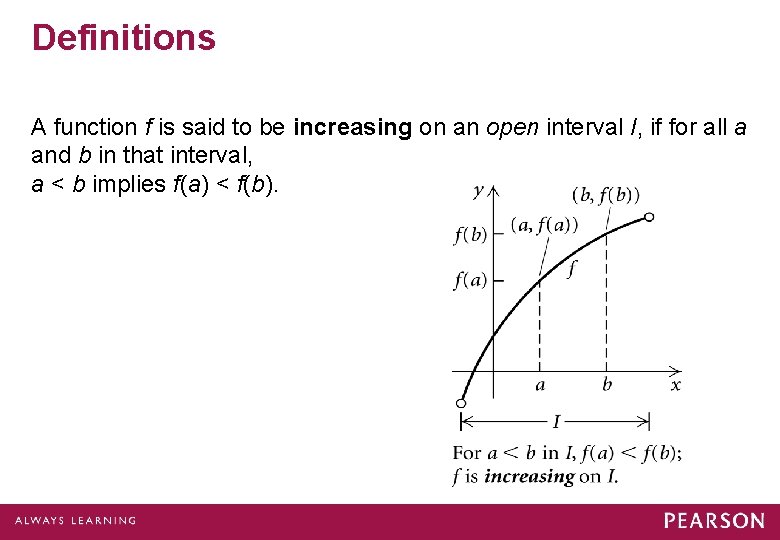
Definitions A function f is said to be increasing on an open interval I, if for all a and b in that interval, a < b implies f(a) < f(b).

Definitions continued A function f is said to be decreasing on an open interval I, if for all a and b in that interval, a < b implies f(a) > f(b).

Definitions continued A function f is said to be constant on an open interval I, if for all a and b in that interval, f(a) = f(b).

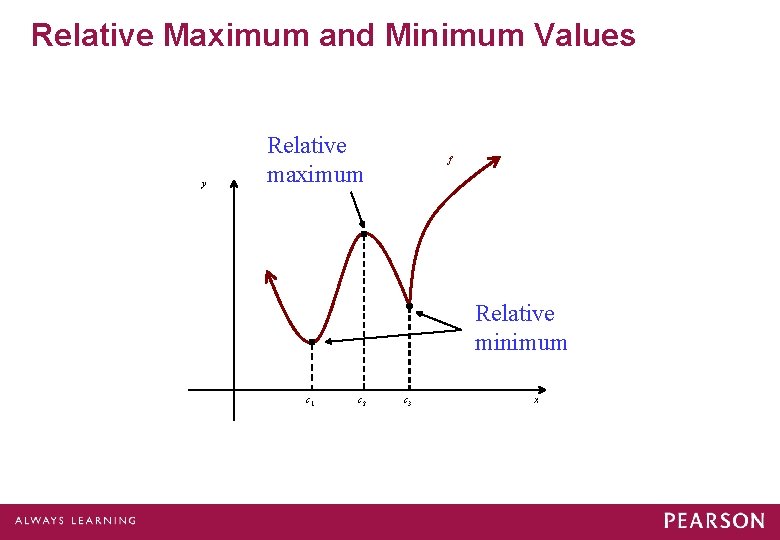
Relative Maximum and Minimum Values Suppose that f is a function for which f(c) exists for some c in the domain of f. Then: f(c) is a relative maximum if there exists an open interval I containing c such that f(c) > f(x), for all x in I where x c; and f(c) is a relative minimum if there exists an open interval I containing c such that f(c) < f(x), for all x in I where x c.

Relative Maximum and Minimum Values y Relative maximum f Relative minimum c 1 c 2 c 3 x

Example Applications of Functions A man plans to enclose a rectangular area using 80 yards of fencing. If the area is w yards wide, express the enclosed area as a function of w. We want area as a function of w. Since the area is rectangular, we have A = lw. We know that the perimeter, 2 lengths and 2 widths, is 80 yds, so we have 40 yds for one length and one width. If the width is w, then the length, l, can be given by l = 40 – w. Now A(w) = (40 – w)w = 40 w – w 2.

Functions Defined Piecewise Some functions are defined piecewise using different output formulas for different parts of the domain. For the function defined as: find f (-3), f (1), and f (5). Since – 3 Since 0 < 1 0, use f (x) = x 2: f (– 3) = (– 3)2 = 9. 2, use f (x) = 4: f (1) = 4. Since 5 > 2 use f (x) = x – 1: f (5) = 5 – 1 = 4.

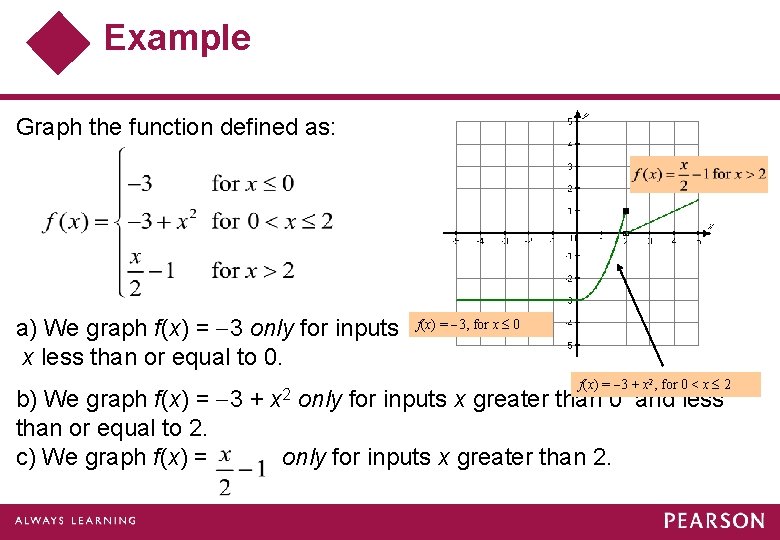
Example Graph the function defined as: a) We graph f(x) = 3 only for inputs x less than or equal to 0. f(x) = 3, for x 0 f(x) = 3 + x 2, for 0 < x 2 b) We graph f(x) = 3 + only for inputs x greater than 0 and less than or equal to 2. c) We graph f(x) = only for inputs x greater than 2. x 2

Functions Defined Piecewise Graph the function defined as: Thus, f(x) = x – 2, for x ≠ ‒ 2 The graph of this part of the function consists of a line with a “hole” at (‒ 2, ‒ 4), indicated by the open circle. The hole occurs because a piece of the function is not defined for x = ‒ 2. f(‒ 2) = 3, so plot the point (‒ 2, 3) above the open circle.

Greatest Integer Function = the greatest integer less than or equal to x. The greatest integer function pairs the input with the greatest integer less than or equal to that input. – 5 0 3