3 3 Increasing and Decreasing Functions Homework p






























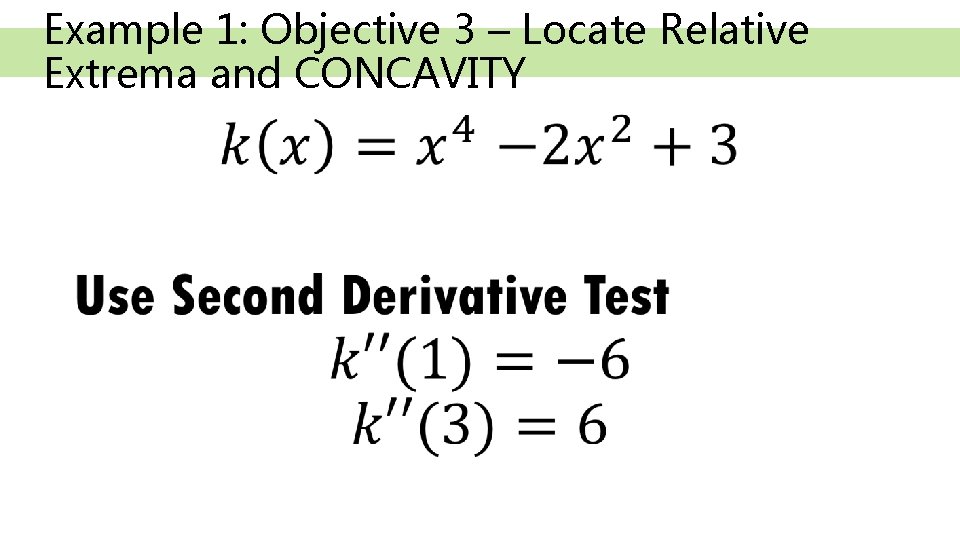


- Slides: 45

3. 3: Increasing and Decreasing Functions Homework: p. 183 5, 9, 15, 25, 39, 47, 57 -69 odd, 73, 83 Standards Learning Objectives: EK 2. 2 A 2: Key • Determine intervals on features of function and their which a function is derivatives can be increasing or identified and decreasing related to their graphical, • Apply the First numerical and Derivative Test to find ANALYTICAL

Lesson Structure 3. 3 3. 4 1 2 3 4 Con Con Con TE TE SLE

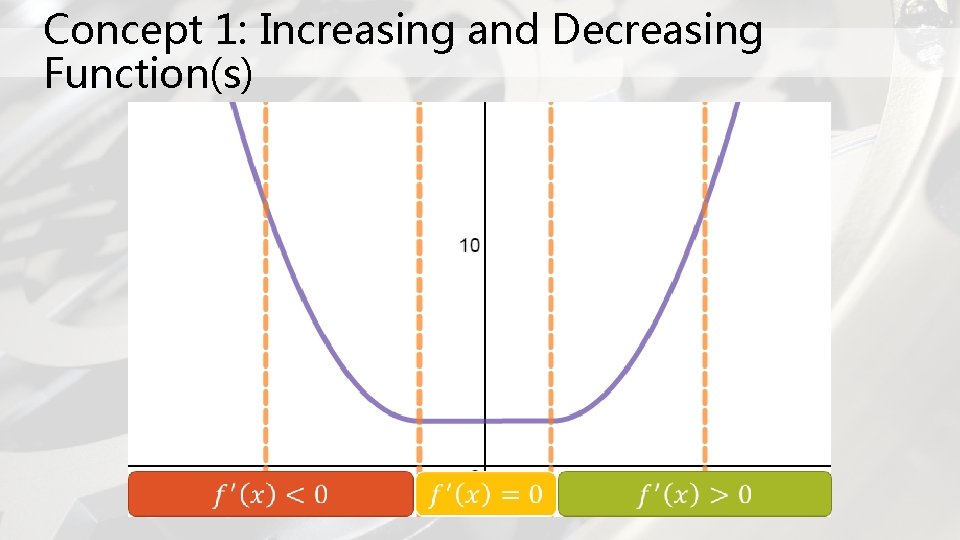
Concept 1: Increasing and Decreasing Function(s)

Concept 1: (extended) – Guidelines for Finding Intervals Let f be continuous on the interval (a, b). To find the open intervals on which f is increasing of decreasing, use the following steps: 1. Locate the critical numbers (by finding the derivative) of f in (a, b) and use these numbers to test intervals 2. Determine the sign of f’(x) at one test value in each interval 3. Based on the sign of f’(x) determine if the function increases or decreases

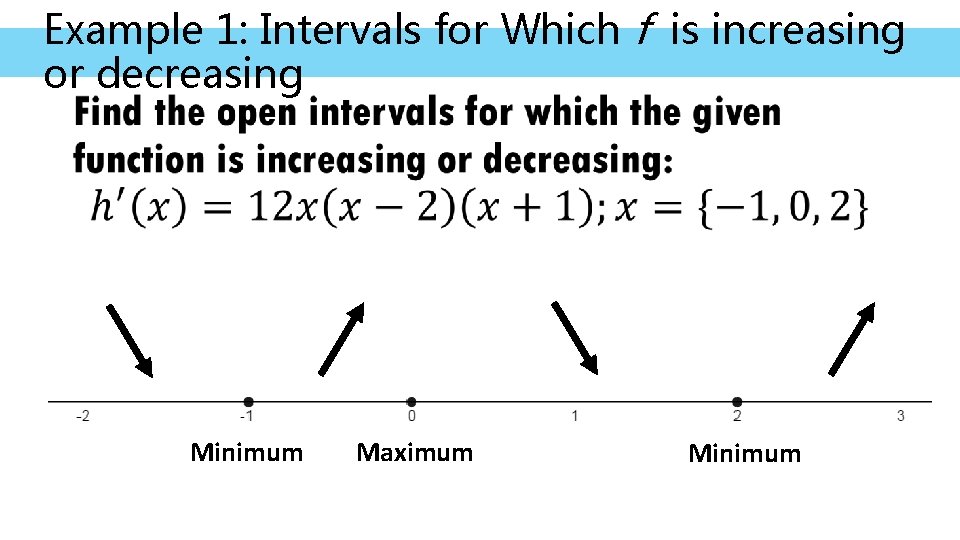
Example 1: Intervals for which f is increasing or decreasing •

Example 1: Intervals for which f is increasing or decreasing •

Example 1: Intervals for Which f is increasing or decreasing •

Example 1: Intervals for Which f is increasing or decreasing •

Example 1: Intervals for Which f is increasing or decreasing •

Example 1: Intervals for Which f is increasing or decreasing • Minimum Maximum Minimum

Example 1: Intervals for which f is increasing or decreasing • Minimum Maximum Minimum

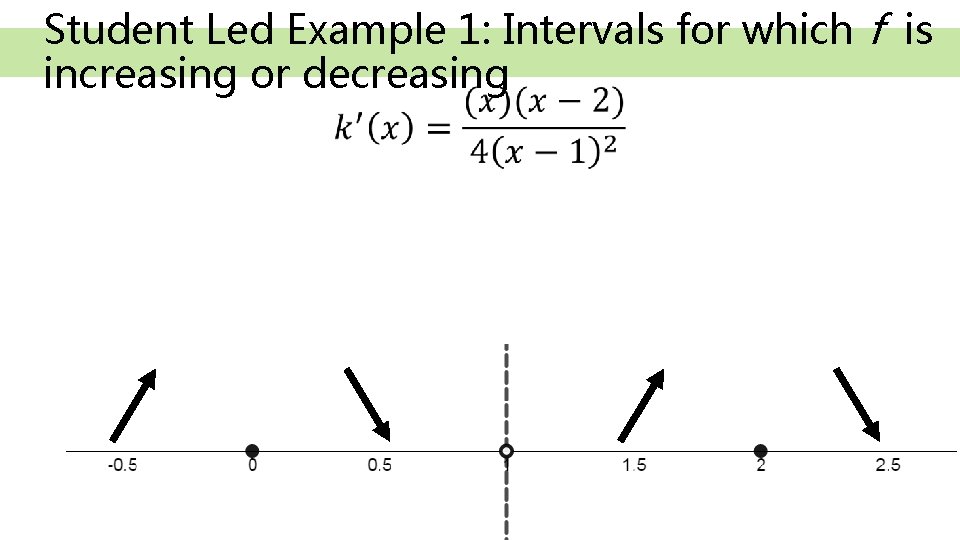
Student Led Example 1: Intervals for which f is increasing or decreasing • m o d t n ra d do re

Student Led Example 1: Intervals for which f is increasing or decreasing •

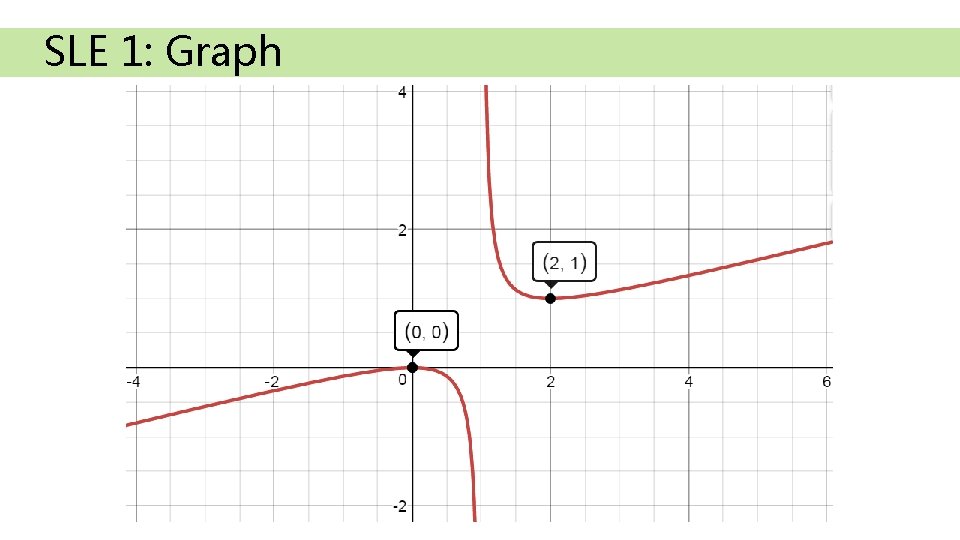
SLE 1: Graph

Concept 2: The First Derivative Test

Concept 2: The First Derivative Test

Concept 2: The First Derivative Test

Concept 2: The First Derivative Test


3. 4: Concavity and the Second Derivative Test Homework: p. 192 9, 15, 21, 25, 29*, 33 -41 odd, 75, Learning 77 Standards Objectives: EK 2. 2 A 1: First and second derivatives of a function can provide information about the function an its graph including intervals of increase or decrease, local and • Determine intervals on which a function is concave up or concave down • Find any points of inflection of the graph of a function • Apply the Second

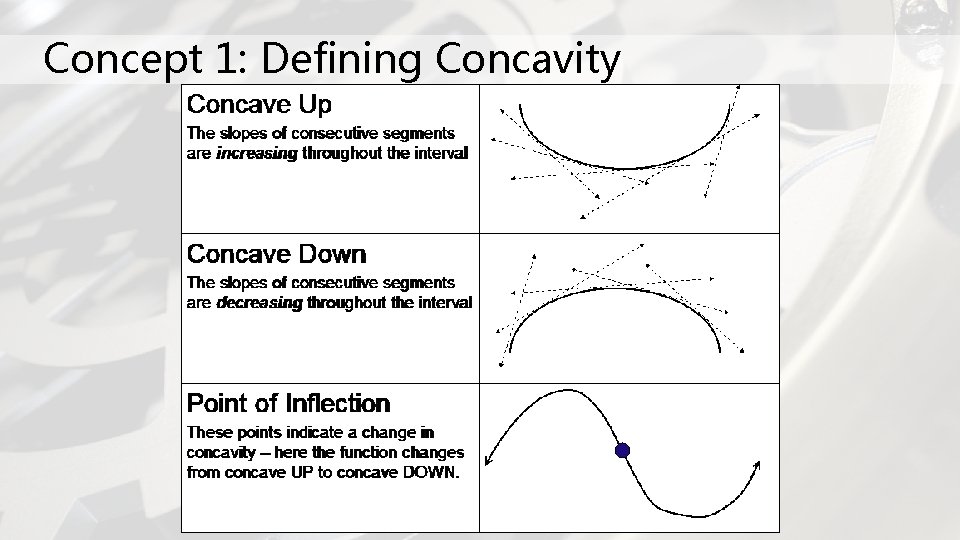
Concept 1: Defining Concavity

Concept 1: Defining Concavity

Concept 2: Test for Concavity

Concept 3: Finding Points of Inflection

Concept 4: The Second Derivative Test

We’re going to try and accomplish all our objectives in one problem. But first, some concepts Wha’?

1. Find all critical points of a function 2. Determine intervals for which a function is increasing or decreasing 3. Locate relative extrema and concavity 4. Find points of inflection using the second derivative test 5. Graph the function 6. Do it all without technology

Example 1: Objective 1 - Find all critical points of a function •

Example 1: Objective 2 – Determine Increasing/Decreasing Intervals •

Example 1: Objective 3 – LOCATE RELATIVE EXTREMA and Concavity •

Example 1: Objective 3 – Locate Relative Extrema and CONCAVITY •

Example 1: Objective 4 – Find Points of Inflection •

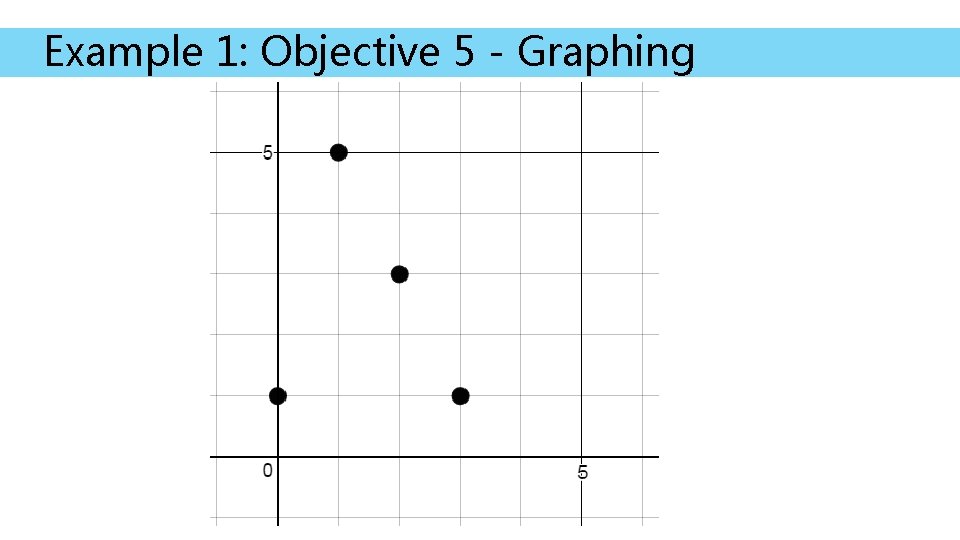
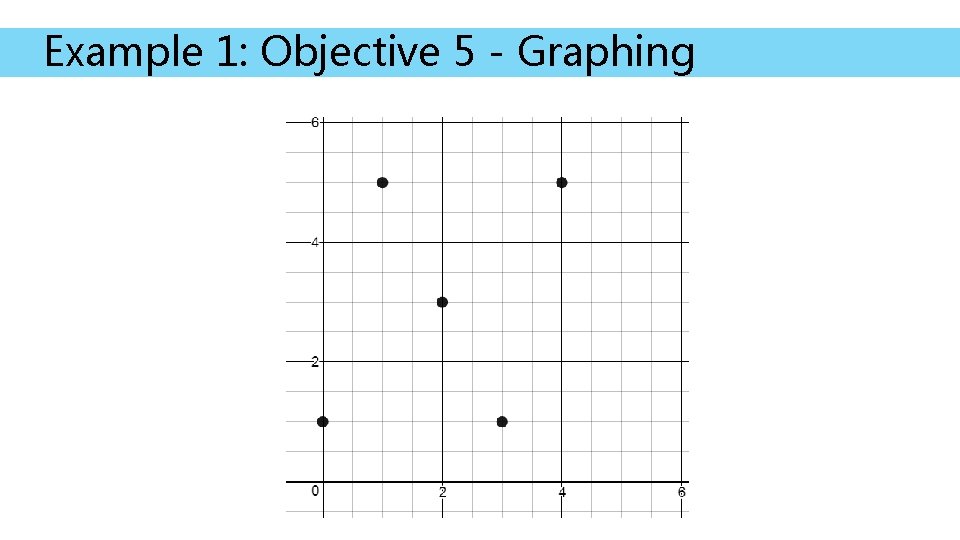
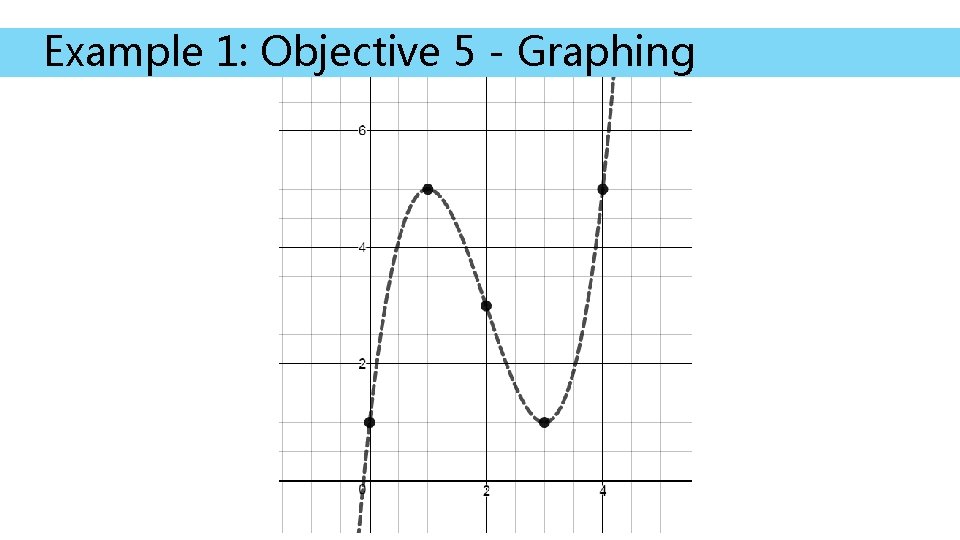
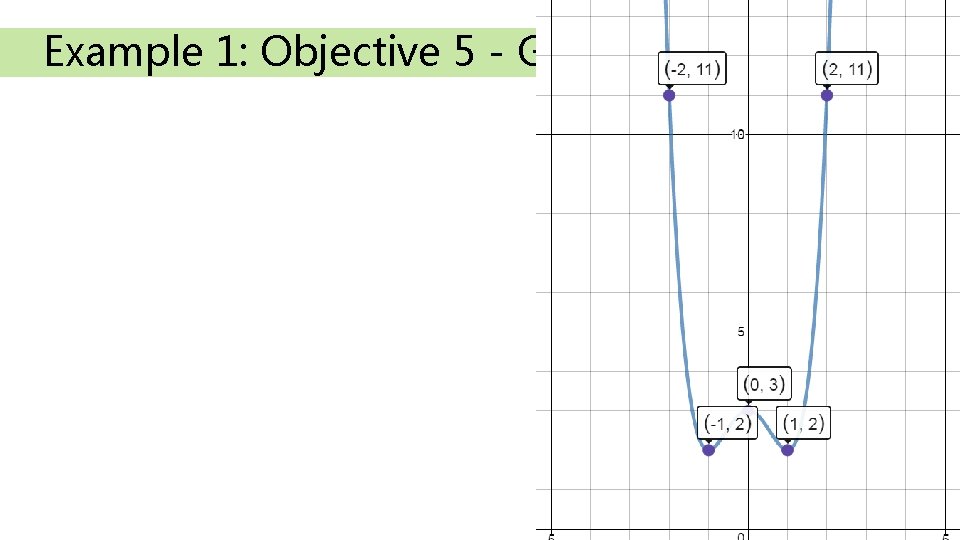
Example 1: Objective 5 - Graphing

Example 1: Objective 5 - Graphing

Example 1: Objective 5 - Graphing

Example 1: Objective 5 - Graphing

Example 1: Objective 1 - Find all critical points of a function •

Example 1: Objective 2 – Determine Increasing/Decreasing Intervals •

Example 1: Objective 3 – LOCATE RELATIVE EXTREMA and Concavity •
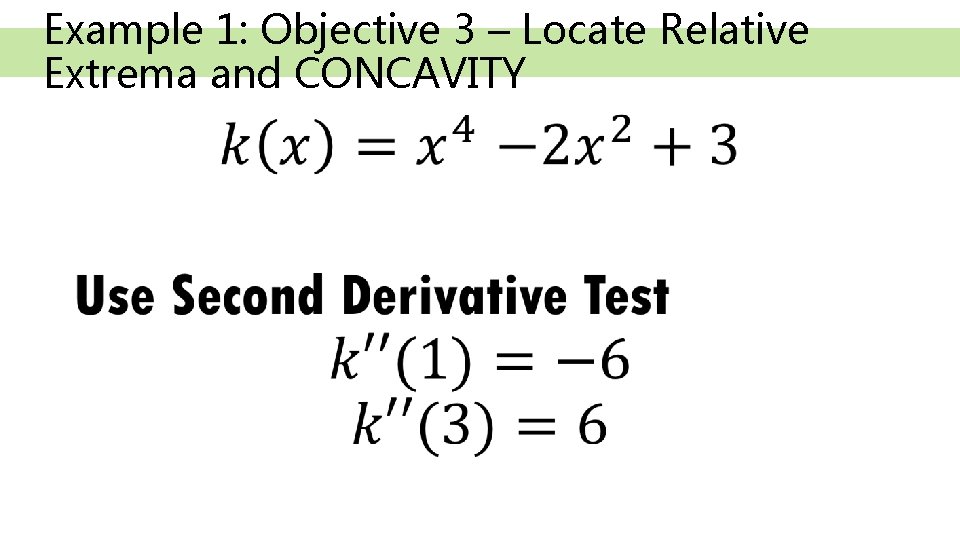
Example 1: Objective 3 – Locate Relative Extrema and CONCAVITY •

Example 1: Objective 4 – Find Points of Inflection SKIP

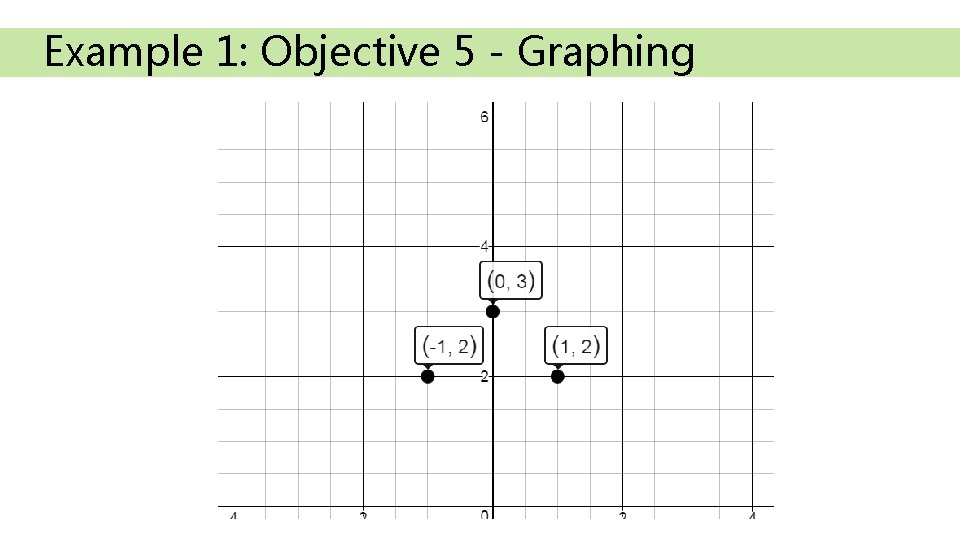
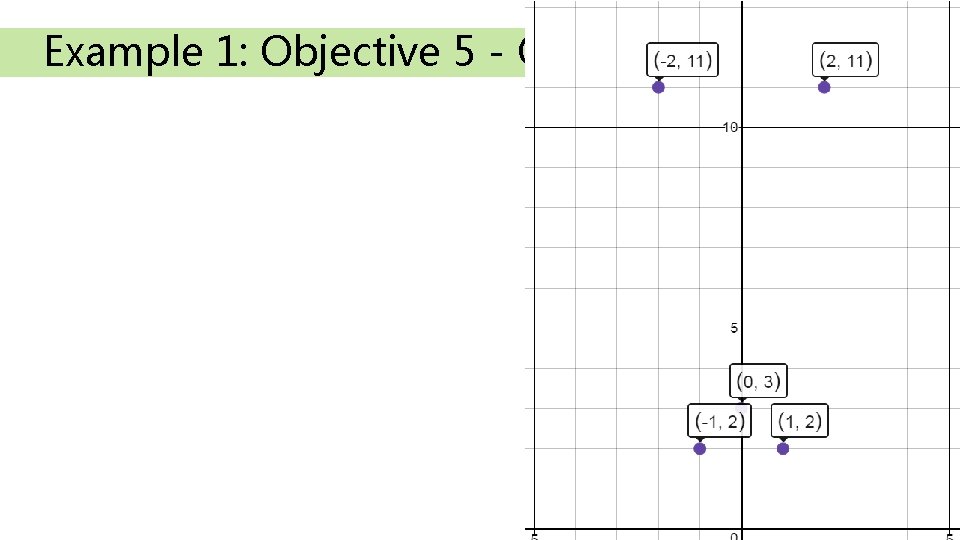
Example 1: Objective 5 - Graphing

Example 1: Objective 5 - Graphing

Example 1: Objective 5 - Graphing

Example 1: Objective 5 - Graphing